Fizikai Szemle 1984/3-4 - Radnai Gyula: Hogyan vezette be Clausius az entrópiát?

Hogyan vezette be Clausius az entrópiát?

Radnai Gyula
ELTE Általános Fizika Tanszéke

1872-ben az akkor 50 éves Rudolf Clausius bonni egyetemi tanárt Helmholtz és Kirchhoff társaságában a Magyar Tudományos Akadémia tiszteleti tagjává választották. Nem mindennapi esemény volt ez: akkor már több mint tíz éve nem került sor arra, hogy külföldi fizikust a Magyar Tudományos Akadémia tagjai sorába válasszon. (A Magyar Tudományos Akadémia első fizikus tiszteleti tagja 1847-től Poncelet volt, aki 1829-ben bevezette a munka egzakt fogalmát.)

Az "áttörést" az európai szemléletű, messzelátó politikus, Eötvös József készítette elő, aki 1867-től (az osztrák-magyar kiegyezéstől) kezdve 1871-ig (haláláig) egyidejűleg volt vallás- és közoktatásügyi miniszter, s a Magyar Tudományos Akadémia elnöke. Fiát, Eötvös Lorándot 1868-ban Heidelbergbe küldte egyetemre, ahol akkor Helmholtz és Kirchhoff tanított. Külföldi tanulmányai során Eötvös Loránd állandó levelezésben állt apjával, s 1870-ben, amikor hazatért Heidelbergből, az ott summa cum laude doktorátust szerzett ifjú bizonyára befolyásolta apját elhatározásában, hogy az akkor legnagyobb német fizikusokat hívja meg a Magyar Tudományos Akadémia tagjai közé (Minisztersége idején Eötvös József nemcsak fiát de számos fiatal tehetséget küldött külföldi egyetemre, tanulmányutakra. Köztük volt Kármán Mór, a huszadik század egyik világhírű, magyar származású mérnök-fizikusának Kármán Tódornak az édesapja is. A 26 éves Kármán Mórt azért küldi Lipcsébe Eötvös József, hogy az ottani tanárképzést tanulmányozza. Két éves tanulmányútján szerzett tapasztalatai alapján szervezte meg 1871-ben Kármán Mór a budapesti tanárképző intézetet és, a gyakorló gimnáziumot.)

Az 1867-et követő néhány évben a magyar szellemi és tudományos életben érezhető fellendülés következett be, az európai szellemi áramlatok rendkívül gyorsan hatottak Magyarországon. 1868-ban indította meg az akkor 30 éves Szily Kálmán a tudományos ismeretterjesztés első magyarországi folyóiratát, a Természettudományi Közlönyt. Tudományos munkásságában Clausius nyomdokain haladt, Boltzmannhoz hasonlóan Szily Kálmán is a clausiusi hőelmélet mechanikai megalapozásán dolgozott. Bizonyára neki is szerepe volt abban, hogy Helmoltzon és Kirchhoffon kívül éppen Clausiust választották meg 1872-ben a Tudományos Akadémia tiszteleti tagjának.

Rudolf Clausius akkor a hőelmélet egyik legnagyobb szaktekintélyének számított a kontinensen. Már hét év telt el azóta, hogy a második főtétel még világosabb megfogalmazása érdekében bevezetett egy új fizikai mennyiséget, amelyet entrópiának nevezett el. Valóban, az entrópia bevezetésére Clausiust azok a meg nem értést tükröző, vagy éppen a második főtétel kimondásában a prioritást vitató írások ösztönözték, amelyek az 1850-es években és a 60-as évek elején jelentek meg. Abban az időben Clausius a gázok kinetikai elméletének kiépítésén dolgozott. Olyan versenytársai voltnak, mint Maxwell; Clausius 1857-ben publikálta kinetikai gázelméletét, Maxwell 1860-ban vezette le a gázok sebességeloszlását.

Kénytelen volt azonban időről-időre visszatérni a második főtételnek általa először 1850-ben kimondott állításához. Az alapvető eszmén semmit sem változtatott, de egyre világosabb és érthetőbb formát keresett állítása megfogalmazásához. Így jutott el 1865-ben az entrópia fogalmához.

Ahhoz, hogy gondolatmenetét megértsük, szellemi produkcióját kellőképp értékelni tudjuk, bele kell élni magunkat abba a helyzetbe, amiben Clausius volt 1844-ben, 22 éves korában, miután a berlini egyetemen gimnáziumi tanári diplomát szerzett.

Szüleinek 18 gyermeke közül Clausius hatodikként született. Édesapja Carl Gottlieb protestáns lelkész és iskolatanácsos volt, az ő iskolájában tanult Clausius gyermekkorában. Később elvégezte a stetteni gimnázium két utolsó osztályát; és 1840-ben iratkozott be a berlini egyetemre. Itt matematikát, fizikát, történelmet hallgatott, többek között Dirichlet, Steiner, Ohm és Magnus voltak a tanárai. A tudomány iránti elhívatottságától vezetve változtatta meg nevét Gottliebről Clausiusra, ebben is követve a francia felvilágosodás gyakorlatát (gondoljunk csak például Descartes-Cartesius-ra). Egyetemi évei alatt házitanítóságot is vállalt, hogy keresetével segítse szüleit a sok gyerek eltartásában. 1844-ben, az egyetem elvégzése után a berlini Friedrich Werder féle gimnáziumba került. Itt tanított 1850-ig. Ez a hat év - volt Clausius talán legtermékenyebb időszaka, alapvető eszméi ekkor születtek meg. Szerencsés körülménynek mondható, hogy a hőtan fejlődésében is rendkívül forrongó időszak volt ez, kiélezett problémákkal, melyek megoldása fiatal, tehetséges koponyákat igényelt.

Clausius, a berlini gimnáziumi tanár, rendszeresen résztvett a berlini fizikai társaság ülésein, előadásain, bekapcsolódott a vitákba. Itt olvasta fel 1847 június 21-én egy fiatal, 26 éves katonaorvos nevezetes értekezését "Az erő megmaradásáról", melyben tulajdonképpen az energia megmaradására vonatkozó kísérleti adatait és elméleti megfontolásait foglalta össze. A katonaorvos Helmholtz volt, aki csak azért végzett katonai orvosi főiskolát, mert ott ingyenes volt az oktatás, de közben már rendszeresen látogatta Magnus laboratóriumát a Spree partján. (Az épület - a "Magnus ház" - ma is áll, az NDK Fizikai Társaságának központi épülete, Helmholtznak pedig szobra áll az egyetem mellett .... )

Helmholtz ismerte Joule 1845-ben publikált méréseit és Robert-Mayer 1842-es eszmefuttatását is. Recsegve-ropogva omlott össze ezekben az években a hőanyag elmélet, teljesen át kellett értékelni a hőről alkotott addigi elképzeléseket.

A naív materialista szemlélet melynek elterjedését a XVIII. század végi felvilágosodás is segítette azt sugallta, hogy minden nagy jelenségcsoportban kell találni valamilyen jellegzetes matériát amelynek mennyisége a folyamatok során változatlan marad. Így vált a tömeg az anyagmennyiség megmaradó mértékévé a kémiai folyamatokban. Így vezették be a Q töltést mint az elektromosság megmaradó kvantitását az elektromos jelenségek körében. És így sikerült Blacknek egy mérési utasítással megadható Q hőkvantitást fogalmilag is megkülönböztetni a hőmérséklettől 1760 körül.

Joule kísérletei most nemcsak arról győztek meg, hogy a Q hőkvantitás nem megmaradó mennyiség, hanem arról is, hogy a hőmennyiségnek Joule kifejezésével élve - "mechanikai egyenértéke" van, amely munkával fejezhető ki. A praktikus gondolkodású Joule-t cseppet sem zavarta, hogy eltűnt a fizikából egy megmaradónak gondolt alapmennyiség. Annál inkább zavarta ez a filozófiailag iskolázottabb Robert Mayert és Helmholtzot, akik erősen hittek valamilyen ok-, erő-hatásmennyiség megmaradásában, s így jutottak el az energia általános fogalmához.

Clausiusnak nem okozott gondot Joule és Helmholtz nézeteinek összeegyeztetése, "a mechanikai hőelmélet első főtételének" megfogalmazása. A későbbiek szempontjából is fontos azonban megjegyezni, hogy Clausius mai szóhasználattal élve "mechanikai pontrendszert választ modellanyagul". Egyrészt azért választja ezt, mert a mechanika és a hőelmélet kívánt összekapcsolását ekkor tudja matematikailag is végrehajtani, másrészt azért, mert végső célja az, hogy a hőelmélet alapegyenleteit mechanikai alaptörvényekből vezesse le. A XIX, század közepén egy jó fizikai elmélet még egyértelműen a mechanika törvényein kellett hogy alapuljon, ez volt Helmholtz alapgondolata is.

Clausius így fogalmaz:

" ... Tárgyalásunkban abból a feltevésből akarunk kiindulni, hogy a hő a kisebb test és éterrészecskék mozgásából áll, a hőmennyiség ezen mozgások eleven erőinek az összege. Ehhez a mozgás természetéről semmiféle különleges feltevést nem kell tennünk, hanem csak a munkára és az eleven erőre vonatkozó egyenértéktételt, amely minden mozgásra érvényes, alkalmaznunk kell a hőre is. Az ezáltal keletkező tételt a mechanikai hőelmélet első főtételének tekintjük."

Másutt ezt írja:

" ... Az eleven erő és a munka egyenértéktételéből levezethető a mechanikai hőelmélet első főtétele, amit a munka és a hő egyenértéktételének fogunk nevezni."

Az "egyenérték" kifejezés Joule-tól származik, az eleven erő tételének kiterjesztése Helmholtz ötlete.

Már itt, az első főtétel megfogalmazásakor látszik Clausius kiváló képessége a különböző nézetek összeegyeztetésére. Ez a "rendteremtő" képessége azonban a második főtétel megfogalmazásánál volt igazán segítségére.

Még nem vezették be a fizikában a mechanikai munka egzakt fogalmát, amikor Carnot 1824-ben egy értekezést publikált "A tűz mozgató erejéről ..." és ebben a hőerőgépekkel végeztethető munkát tette vizsgálat tárgyává. Carnot dolgozatában az akkor egyik legsürgetőbb kérdésre igyekezett választ adni: van-e elvi határa a gőzgépek hatásfoka növelésének?

Alapvető elgondolása az volt, hogy a hőerőgépek munkavégzése közben a hő a magasabb hőmérsékletű helyről az alacsonyabb hőmérsékletű helyre vándorol. Ahogyan a lezúduló víz is képes munkát végezni, miközben a magasabb helyről az alacsonyabbra jut, úgy végzi a hő is a munkát, miközben a magasabb hőmérsékletű helyekről az alacsonyabb hőmérsékletű helyekre folyik át. Az analógiát tovább is vitte: ahogyan a víz mennyisége esés közben változatlan marad, ugyanúgy a hő mennyisége is változatlan marad, miközben munkát végez.

Általánosabban megfogalmazva Carnot gondolatát, azt mondhatjuk, hogy az ő elképzelése szerint a hőmennyiség úgy áramlik az egyik hőmérsékletű helyről a másikra, mint valamilyen (pl. gravitációs, elektromos, stb.) töltés az egyik potenciálú helyről a másikra egy konzervatív erőtérben.

Minthogy periodikusan működő gépeket vizsgált, természetesen vezette be a körfolyamat fogalmát, de elméleti fejtegetéseiben a folyamatok megfordításával is operált. Arra a következtetésre jutott, hogy a kéthőtartályos körfolyamatok esetén a gép által végzett munka az átáramló hő mennyiségével arányos, s ezen kívül már csak a két hőmérséklettől függ. A munka és a hő hányadosaként értelmezett hatásfok tehát független a gépben körfolyamatot végző anyagtól! Carnot bonyolult fejtegetéseihez szemléletes grafikus ábrázolást talált 1834-ben Clapeyron, akinek nagy szerepe volt abban, hogy Carnot elméleti. meggondolásai nem jutottak a meg nem értett gondolatok szomorú sorsára, nem kerültek véglegesen a felejtés süllyesztőjébe. Thomson ásta ki újra őket 1847-48-ban, amikor az egyetem elvégzése után egy évig Franciaországban dolgozott.

Az első főtétel megjelenése különös megvilágításba helyezte Carnot elméletét: kiderült, hogy alapfeltevésében hibás. Mi legyen vele? Ki kell dobni, mint túlhaladottat és tarthatatlant, vagy megmenthető valahogy? Jó lenne megmenteni egyrészt azért, mert tényleges gyakorlati igényből keletkezett, másrészt azért, mert Thomson 1848-ban Carnot elmélete alapján vezetett be egy olyan univerzális, elvi fontosságú hőmérsékleti skálát, amelynek segítségével a hőmérséklet mérését hatásfok mérésére - tehát hő és munka mérésére - lehetett visszavezetni. Igenám, de Carnot szerint a hő munkát tud végezni, Joule szerint a munkából hő nyerhető - és a párizsi akadémia már 1775 óta nem fogad el perpetuum mobile tervezeteket. De tréfán kívül: a perpetuum mobile lehetetlensége Carnot érvelésének is egyik sarkalatos pontja volt!

E látszólag kibékíthetetlen ellentmondás feloldása, az ellentétes nézetek összeegyeztetése Clausiusnak való feladat volt. Gimnáziumi tanári pályájának utolsó évében, 1850-ben publikálta Clausius először a megoldást: a hőelméletnek két független főtétele van, amelyek azonban nem ellentétesek egymással, hanem két különböző kérdésre adnak választ.

Joule eredményét, amely szerint a hőnek mechanikai egyenértéke van, Clausius sajátos egyenértéktételnek tekinti, s úgy fogalmazza meg, hogy "minden esetben, amikor a hő munkát végez, a kifejtett munkával arányos hő fogy el", s a hő és a munka egyenérték-tételét tekinti a hőtan első főtételének. Ha egy "egyszerű" körfolyamatban (Clausius így nevezi a Carnot körfolyamatot) "a munkavégző közeg periódusonként Q₁ nagyságú T₁ hőmérsékletű hőt vesz fel és Q₂ nagyságú T₂ hőmérsékletű hőt ad le, akkor Q₁-Q₂ hővel egyenértékű munkát végez."

Carnot elgondolását, hogy a T₁-ről T₂-re menő hő mennyisége változatlan marad, meg lehet menteni, ha csupán a Q2 hőre gondolunk. Clausius nagy ötlete az, hogy a körfolyamatban kétféle átalakulás játszódik le együttesen: hőnek munkává és hőnek hővé való átalakulása. Ez a két átalakulás a megfordítható körfolyamatokban "egyenértékű". Későbbi dolgozataiban sikerült Clausiusnak megadnia azt is, hogyan lehet kiszámítani a "hőből munka", illetve "hőből hő" átalakulások egyenértékeit. Egyszerű, megfordítható Carnot körfolyamatok esetén:

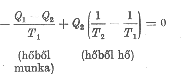
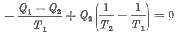
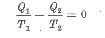
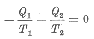
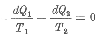
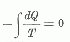
képlet

Látszik, hogy az egyik átalakulás pozitív, a másik negatív "egyenértékű": magát az egyenértékűséget Clausius úgy érti, hogy a két átalakulás a reverzibilis körfolyamatban "kompenzálja egymást."

Clausius megkülönböztet pozitív és negatív átalakulásokat, folyamatokat. Pozitívnak tekinti a munka átalakulását hővé például súrlódás során, vagy a melegebb testről a hidegebb testre történő hőátmenetet. Negatív folyamat a hő átalakulása munkává, vagy az az eset, amikor hő megy át hidegebb testről melegebbre. A pozitív folyamatok maguktól is végbemehetnek, a negatív folyamatok azonban. csak akkor, ha egyidejűleg pozitív folyamatok is lejátszódnak, amelyek kompenzálják őket. Ez történik minden megfordítható körfolyamatban.

Clausius megfogalmazásában a második főtétel így hangzik:

"Hő magától - kompenzáció nélkül - nem képes átmenni a hidegebb testről a melegebbre."

Ezzel Clausius az egyik, általa negatívnak tartott folyamat spontán lejátszódásának lehetetlenségét mondja ki második főtételként. Miért éppen ezt a folyamatot választotta? Valószínűleg azért, mert ekkor a hősugárzás kutatása az érdeklődés előterében állt (gondoljunk csak Kirchhoff alapvető eredményeire ezen a területen) és Clausius közben 1848-ban Halleban védte meg doktori disszertációját, melynek témája a szivárvány és más légköri és sugárzási jelenségek voltak. Milyen magas hőmérsékletre lehet hevíteni egy testet a Nap sugárzásának fókuszolásával? Izgalmas kérdés; amelyre bizonyára Clausius is kereste a választ. Ezt írta:

"A hő hidegebb testből melegebb testbe magától átmenni nem képes ... Eszerint a sugárzásra vonatkozó korábbi ismereteinket ki kell egészítenünk, még olyan esetben is, amikor a sugarak iránya törés vagy visszaverődés folytán bárhogy megváltozik és ezáltal a sugarak koncentrálódnak ..."

Csupán a megfordítható körfolyamatokra szorítkozva a második főtételt Clausius egyenérték-tételként tudta megfogalmazni. Ebből az egyenértéktételből logikai út vezet az. entrópia fogalmához. Az út főbb állomásai a következők:

Egyszerű-Carnot-körfolyamatra:

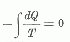képlet

Ebből az egyenletből rendezés után kapjuk:

képlet

Ha a hőmennyiségeket előjeles mennyiségeknek tekintjük úgy, hogy a körfolyamatot végző test által leadott (vagyis a hőtartályok által felvett) hőmennyiséget tekintjük pozitívnak; akkor Q₁ < 0, Q₂ > 0, tehát

képlet

Differenciálisan kis izotermaszakaszokat tartalmazó egyszerű körfolyamatra:

képlet

Tetszőleges reverzibilis körfolyamatot differenciális egyszerű körfolyamatokra bontva és összegezve:

képlet

egyenletet Clausius 1854-ben írta fel először. De csak több mint tíz évvel később, 1865-ben vezette be a

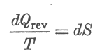
képlet

definícióval azt az S átalakulási függvényt, amelyet entrópiának nevezett el. (A görög τρoπη szó átalakulást, átváltozást, átfordulást jelent, ebből alkotta meg Clausius az entrópia szót. Az eredeti görög kifejezés több ma is használatos szavunk gyökere. A "trópus" azt az éghajlati övet jelenti, amely az északi és a déli félgömböt választja el egymástól. "Trópikus" év a napfordulóra vonatkozó év. A "tropizmus" a növények valamilyen irányba való fordulása, pl. fototropizmus, geotropizmus, stb. 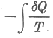Szépirodalomban a szóképet, a képletes - megváltozott értelmű - kifejezést nevezik trópusnak, zenében pedig a gregorián énekek díszítő dallamfordulatait.)

A továbbiakban Clausius arra a következtetésre jutott, hogy az

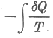N = képlet

kifejezés nem megfordítható körfolyamatok esetén csak pozitív lehet. Ezt írta:

"Az előzőekben már láttuk, hogy egy megfordítható körfolyamatban az átalakulások egyenértékösszege nullával egyenlő. Egy átalakulási formára - nevezetesen a különböző hőmérsékletű testek közötti hővezetésre - egy, a hő lényegén alapuló alaptételt fogadtunk el: azaz alacsonyabb hőmérsékletről magasabb hőmérsékletre (amely negatív átalakulást jelent) hőátmenet kompenzáció nélkül nem lehetséges. Erre támaszkodva bebizonyítottuk, hogy egy megfordítható körfolyamat során az összes fellépő átalakulási értékek összege negatív nem lehet, mert minden visszamaradó negatív átalakulás egy alacsonyabb hőmérsékletről magasabb hőmérsékletre való hőátmenetet jelentene minden más kompenzáció nélkül, ami lehetetlen.

Az átalakulási értékek összege pozitív sem lehet, mert elég csak a körfolyamatunkat fordított irányban végrehajtani és ismét ellentmondásba kerülünk alaptételünkkel.

A bizonyítás első része változatlanul érvényes marad olyan körfolyamatokra is, amelyekben nem megfordítható változások lépnek fel, tehát az átalakulási értékek összege negatív nem lehet.

Természetesen az ilyen körfolyamatokra már nem igaz, hogy az átalakulási értékek összege pozitív sem lehet. Kísérleti tények szólnak amellett, hegy ez az összeg pozitív lesz, ha a vizsgált körfolyamat nem megfordítható: pl. a súrlódás következtében keletkezett hő vagy egy melegebb testből hidegebb testbe való spontán hővezetés önmagában pozitív átalakulási értékű.

Tehát a korábban kimondott tételt a következőképpen egészíthetjük ki:

Egy körfolyamat során fellépő átalakulások egyenértékösszege csak pozitív, vagy határesetben nulla lehet.

Az olyan átalakulásokat, amelyek egy körfolyamat végén minden egyéb ellentétes átalakulás nélkül fennmaradnak, kompenzálatlan átalakulásoknak nevezzük.

Ezek szerint a fenti tételt egyszerűbben is megfogalmazhatjuk:

A kompenzálatlan átalakulások csak pozitívak lehetnek.

Az így kibővített tétel matematikai alakjának megkereséséhez csak emlékeztetnünk kell, hogy körfolyamat során az átalakulási értékek összegét

integrál értéke adja.

Ennek megfelelően az egyenletek általánosan - tehát mostmár akár megfordítható, vagy nem megfordítható folyamatokra - a következők lesznek:

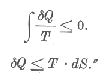
képlet

Már csak egy fontos kérdés van hátra. Hogyan jutott Clausius eredetileg az átalakulási egyenértékek kiszámítási formuláihoz ?

Ezt a gondolatmenetet most azért közöljük részletesebben is az ő megfogalmazásában, mert így nyerhetünk valamelyes betekintést abba a módszerbe, ahogyan Clausius érvelt és gondolkodott:

"Az egyenérték mértékére vonatkozóan mindenek előtt világos, hogy a munkának hővé való átalakulási értéke a keletkezett hő mennyiségével arányos kell legyen, és ezenkívül már csak annak hőmérsékletétől függhet. Tehát ha a munka T hőmérsékletű Q hőmennyiséggé alakul át, az átalakulás egyenértékét teljesen általánosan a Q · f (T) kifejezéssel adhatjuk meg, ahol f (T) minden esetben ugyanaz a hőmérsékletfüggvény.

Amennyiben a formulában szereplő Q hőmennyiség negatív, akkor ez azt fejezi ki, hogy a Q hőmennyiség nem munkából hővé, hanem hőből munkává alakult át.

Hasonlóképpen a T₁ hőmérsékletről T₂ hőmérsékletre átvezetett Q hő átalakulási értéke arányos kell legyen az átvezetett hő mennyiségével, és ezenkívül már csak a két hőmérséklettől függhet:

Q · F(T₁, T₂), ahol F (T₁, T₂) a két hőmérsékletnek minden esetben ugyanazon függvénye, melynek pontos alakja jóllehet közelebbről még nem ismert, azonban az már eleve világos, hogy ebben a függvényben a két hőmérsékletet felcserélve a függvényérték előjele ellentétes kell legyen anélkül, hogy numerikus értéke megváltozna:

F (T₂, T₁) = - F (T₁, T₂). (1)

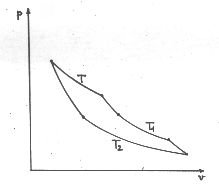
A kapott átalakulási értékeket a fenti ábrával szemléltetett megfordítható körfolyamatra alkalmazva, - ebben a T hőmérsékletű Q hőmennyiség munkává alakul, aminek átalakulási értéke Q& middot; f (T) és Q₁ hőmennyiséget pedig T₁ hőmérsékletről T₂-re vezetünk át, aminek átalakulási egyénértéke Q₁ · F (T₁,T₂), érvényes kell legyen a

- Q · f (T) + Q₁ · F (T₁, T₂) = 0 (2)

Az ábrán szemléltetett körfolyamatot fordított irányban úgy hajtsuk végre, hogy a K₁ és K₂ hőtartályok, valamint a közöttük átvezetett Q₁ hő ugyanaz maradjon mint korábban, de a T hőmérsékletű K hőtartály helyett egy másik T' hőmérsékletű K' testet használjunk. Legyen az ebben az esetben a munka árán nyert hő Q', így:

Q' · f (T') + Q₁ · F (T₂ T₁) = 0 (3)

ábra

A (2) és (3) egyenletet összeadva valamint (1) figyelembevételével adódik:

- Q · f (T) + Q' · f (T') = 0 (4)

A két egymás után végrehajtott, körfolyamatot tekinthetjük egyetlen körfolyamatnak is. Ebben a K₁ és K₂ közti hőátmenetek már nem jönnek számításba, kölcsönösen kiegyenlítik egymást, tehát csak a K hőtartályból elvont és munkává alakult Q hőmennyiséget, valamint a munka árán keletkezett és K' által felvett Q' hőmennyiséget kell figyelembe venni. Ez a két ugyanazon jellegű hő → munka átalakulás azonban felbontható két különböző jellegű átalakulásra. Nevezetesen úgy, hogy a Q és Q' hőmennyiségekben közösen meglevő rész minden további nélkül a K testből a K'-be vezetődik át, a fennmaradó rész pedig munkává alakul át (vagy fordítva, attól függően, hogy Q vagy Q' a nagyobb).

Legyen a T hőmérséklet nagyobb mint a T', így a hőátvezetés melegebb testből hidegebb test felé irányul, tehát pozitív. Eszerint a másik átalakulás negatív kell legyen, tehát hő alakul át munkává, amiből következik, hogy a K által leadott Q hő nagyobb mint a K' által felvett Q'. Most bontsuk fel gondolatban a Q hőmennyiséget két részre: Q' és Q-Q'-re, ahol az első a K hőtartályból a K'-be átvezetett, utóbbi pedig a munkává átalakult hőmennyiséget jelenti. Ezen felfogás szerint a fent leírt kettős folyamat ugyanolyan jellegű folyamatnak tekinthető, mint azok a folyamatok, amelyekből az összetevődött, tehát a Q' és Q-Q' hőmennyiségekre (2)-höz hasonló összefüggés érvényes:

- (Q - Q') · f (T) + Q' · F (T,T') (5)

A (4)-es és (5)-ös egyenletekből egyszerű átalakítások után a következő egyenletet kapjuk:

F(T, T') = f (T') - f (T)

Tehát a második fajta átalakulási módra vonatkozó hőmérsékletfüggvény teljesen általánosan visszavezethető az első fajta átalakulási módra érvényes hőmérsékletfüggvényre.

Az utóbbi függvény rövidítésére egy egyszerű jelölést veztünk be. Azonban bizonyos okokból célszerű nem magát a függvényt, hanem annak reciprokértékét az új jellel megjelölni:

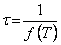
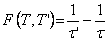
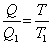
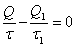
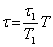
képlet

τ a hőmérsékletnek egy ismeretlen függvénye:

képlet

Az átváltozási értékekben szereplő τ függvény a körfolyamatot végző test anyagi minőségétől független, ezért alakját bármely test állapotváltozásának segítségével meghatározhatjuk. Válasszuk ehhez újra az ideális gázt, és ezzel gondolatban végezzünk el egy egyszerű körfolyamatot, melyben a gáz egy bizonyos T hőmérsékletnél hőt vesz fel, és egy másik T₁ hőmérsékleten pedig hőt ad le. A felvett és leadott hőmennyiségek abszolút értékét jelölje Q, ill. Q₁.

Ideális gáz esetén:

képlet

Másrészt erre az egyszerű körfolyamatra a egyenlet alkalmazva:

képlet

A két egyenletet összevetve a következő összefüggést kapjuk:

képlet

T-t egy tetszés szerinti: T₁-et pedig egy adott hőmérsékletnek tekintve az előző egyenlet a következőképpen írható:

τ = T · constans

s ezáltal a τ hőmérsékletfüggvény egy konstans faktor erejéig meghatározott. A konstans faktor értékeként a legkényelmesebb értéket, az egységet választva:

τ = T

Eszerint a τ hőmennyiségfüggvény minden további nélkül az abszolút hőmérséklettel egyenlő.

A τ hőmérsékletfüggvény itt levezetett meghatározása a gázokra kapott egyenletekre támaszkodik, így az alkalmazásánál a gázokra tett azon feltevés - miszerint egy ideális gáz, ha konstans hőmérsékleten kitágul, csak annyi hőt vehet fel amennyi külső munkát végez - olyan megszorítás, amelyen a meghatározás alapszik. Ha valakinek ezek miatt kételye támad ezt a meghatározást teljesen megbízhatóként elismerni, akkor az a τ-val jelölt hőmérsékletfüggvényt még ismeretlenkén megtarthatja. Azonban nézetem szerint az ilyen kétely nem indokolt, ezért a továbbiakban τ helyén mindig T áll majd."

1865-ben Clausius már világosan látta, hogy mindkét főtétel egy-egy állapotjelzőt rendel a testhez, és azt is tudta, hogy sem a hő, sem a munka nem lehetnek állapotjelzők.

A belső energia fogalmát "molekulárisan" is értelmezte gázokra, az entrópia fogalmához azonban nem fűzött semmilyen molekuláris értelmezést.

Hangsúlyozta, hogy az entrópia a test jellemzője, de az entrópia változását úgy értelmezte, mint a reverzibilisen átalakuló hő átalakulási egyenértékét. Clausiusnál még a hőnek is volt hőmérséklete, s a hő átalakulási egyenértéke jelentette az entrópiaváltozást.

Nem csoda, hogy az entrópia mikroszkópikus értelmezése a legnagyobb elmék hosszú, fáradságos munkája nyomán született csak meg.

Clausius szellemi alkotása még évtizedekig jelentett kihívást a fiatal tehetségek számára. Elég, ha két példát említünk:

1866-ban, egy évvel a clausiusi entrópia megszületése után a 22 éves Boltzmann doktori disszertációjának témájául a második főtételnek mechanikai elvekből való levezetését választotta.

1879-ben, három évvel Clausius összegyűjtött munkáinak első kiadása után a 21 éves Planck doktori disszertációjában a clausiusi második főtételt vetette szigorú kritikai elemzés alá.

Mit nyújthat a mai fizikatanár számára a clausiusi entrópiafogalom megismerése?

Biztosan segít megérteni, mi köze az entrópiának a szó görög eredetijéhez.

Valószínűleg élvezetet okoz megismerni Clausius szintetizáló elméletalkotó módszerét.

Lehet, hogy felkelti az érdeklődést Boltzmann, Planck vagy éppen Szily Kálmán kutatásai iránt, melyekhez Clausius alkotása adta az ösztönzést.

De jó lenne, ha emellett még növelné a mai középiskolai tanárok alkotókedvét, önbizalmát az a felismerés, hogy az az ember, akiben ezek az ötletek megszülettek, gimnáziumi tanár volt.

Igaz, több mint 130 évvel ezelőtt.

A felhasznált legfontosabb forrásmunkák:

Rudolf Clausius: Die mechanische Wärmetheorie. Braunschweig, 1876.
Zábrádi Antal: Clausius élete és termodinamikai munkássága (Szakdolgozat) ELTE, 1976.

Fizikai Szemle honlap

Tartalomjegyzék

Hogyan vezette be Clausius az entrópiát?