Fizikai Szemle honlap |
Tartalomjegyzék |
Ladik János, Peter Saalfrank és Richard F. Wood
Erlangen-Nünbergi Egyetem Elméleti Kémiai Intézete
Bevezetés
A magashőmérsékletű szupravezetés létezését már 1950 óta több elméleti szakember is előre jelezte. Már ebben az évben Superfluids című könyvének bevezetőjében [1] London tette fel azt a kérdést, hogy "előfordulhat-e szuperfolyékony jellegű állapot bizonyos olyan makromolekulákban, amelyek biokémiai reakciókban is fontos szerepet játszanak". Little [2] 1964-ben közölt egy cikket amelyben magas (szoba-) hőmérsékletű szupravezetés létezését. jósolta meg olyan mozgékony elektronokat tartalmazó hosszú láncokban, amelyeknek oldalláncaiban lokalizált elektronok vannak. Az ilyen lokalizált állapotok polarizációját első rendben az ún. "virtuális excitonok" segítségével írhatjuk le ("a magashőmérsékletű szupravezetés exciton elmélete"), amelyek ugyanazt a szerepet töltik be, mint a fononok a szupravezetés megszokott elméletében.
Így aztán a BCS-típusú elméletek [3] erre az esetre is alkalmazhatók, de az (me/Mnukleon) = 1840 tömegarány következtében az átmeneti hőmérsékletet Little
![]() 2000 K körüli értékre becsülte.
2000 K körüli értékre becsülte.
Két fontos ellenérv szól az előbbi elmélet ellen. Először is - ahogy azt több szerző is hangsúlyozta (lásd pl. [4]) - egydimenziós rendszerekben a termodinamikai fluktuációk zavaró hatása miatt hosszú távú rendezettség nem alakulhat ki. Egy további cikkében [5] Little arra a következtetésre jutott, hogy az olyan egydimenziós rendszerekben ahol a másik két dimenzió nem egzaktul nulla (kvázi -1D rendszerek), a környezeti hatások következtében lokálisan mégiscsak erősen megnövekedhet a vezetőképesség a lánc bizonyos szakaszaiban. A valóságban azonban a meglehetősen nagy kísérleti erőfeszítések ellenére sem találtak kvázi-egydimenziós magashőmérsékletű szupravezetőket.
A másik nehézség Little elméletével kapcsolatban az a tény - amint azt a szerzők egyike (L.J.) Biczóval és Zawadowskival együtt már 1965-ben megmutatta [6] -, hogy a részletes kvantumkémiai számítások szerint a mozgékony és lokalizált elektronok térbeli elkülönülése miatt soha nem kapható a leárnyékolt Coulomb-taszításnál nagyobb abszolút értékű vonzótag. A nehézség leküzdésére ugyanebben a cikkben azt javasoltuk, hogy magashőmérsékletű szupravezetést sokkal inkább egymás felett elhelyezkedő sík molekulák rendszerében várhatunk. Ebben az esetben a
![]() -elektronok mozgékonyak, másrészt a kovalens kötéseket alkotó
-elektronok mozgékonyak, másrészt a kovalens kötéseket alkotó
![]() -elektronok vagy a magányos elektronpárok elektronjai lokalizáltak és így polarizálhatók is, amely a mozgékony
-elektronok vagy a magányos elektronpárok elektronjai lokalizáltak és így polarizálhatók is, amely a mozgékony
![]() -elektronok közötti vonzás, s így párok kialakulásához vezethet. Ebben a modellben nem különülnek el térben egymástól a mozgékony és a polarizálható lokalizált elektronok; megkülönböztetésük csak kvantummechanikai értelemben lehetséges.
-elektronok közötti vonzás, s így párok kialakulásához vezethet. Ebben a modellben nem különülnek el térben egymástól a mozgékony és a polarizálható lokalizált elektronok; megkülönböztetésük csak kvantummechanikai értelemben lehetséges.
Egy a későbbiekben megjelent cikksorozatban [7-9] félempirikus és ab iníció sávszerkezetek alapján megmutattuk, hogy egy rétegezett nukleotid bázis (citozin) láncban a magashőmérsékletű szupravezetés fent vázolt
![]() -exciton elmélete alapján nem zárható ki a szupravezető állapot létezése. Ab iníció számítás esetén például [9] a vezetési sáv alsó szélénél a vonzó tag 2 eV-tal nagyobb a Coulomb-taszításnál. Mindazonáltal a Jérome és Creuzet által a nyolc gyűrűt tartalmazó rétegezett molekulákban kísérletileg talált legmagasabb átmeneti hőmérséklet is csak Tc = 8 K volt [10]. Ezt jelzésnek tekinthetjük arra, hogy magas kritikus hőmérsékletet kétdimenziós rendszerekben kell keresnünk, mivel a kvázi-egydimenziós rendszerekben a fluktuációk magasabb hőmérsékleteken elnyomják a szupravezetést, vagy pedig olyan kis tartományokra lokalizálják azt, hogy a jelenség mérhetetlenné válik.
-exciton elmélete alapján nem zárható ki a szupravezető állapot létezése. Ab iníció számítás esetén például [9] a vezetési sáv alsó szélénél a vonzó tag 2 eV-tal nagyobb a Coulomb-taszításnál. Mindazonáltal a Jérome és Creuzet által a nyolc gyűrűt tartalmazó rétegezett molekulákban kísérletileg talált legmagasabb átmeneti hőmérséklet is csak Tc = 8 K volt [10]. Ezt jelzésnek tekinthetjük arra, hogy magas kritikus hőmérsékletet kétdimenziós rendszerekben kell keresnünk, mivel a kvázi-egydimenziós rendszerekben a fluktuációk magasabb hőmérsékleteken elnyomják a szupravezetést, vagy pedig olyan kis tartományokra lokalizálják azt, hogy a jelenség mérhetetlenné válik.
1970-ben Ginzburg egy váltakozóan elrendezett vezető és szigetelő sávokból álló háromdimenziós modellt ismertetett [11]. Feltételezte; hogy a vezető rétegekben lévő mozgékony elektronok alagútjelenség következtében átjutnak a szigetelő rétegekbe és így polarizálják az ott lévő lokalizált elektronokat. (Ebben a modellben az egyes sávok szélessége nem csak egy atomra terjed ki, azaz a sávok nem mikroszkopikus méretű rétegek, mint a következőkben tárgyalandó kerámikus anyagok esetében.) Így itt is a szigetelőkben lévő elektron-eloszlás polarizációja adja a vonzó kölcsönhatást a vezető rétegekben lévő mozgékony elektronok között. Vegyük azt is észre, hogy feltételezve a vezető réteg elektronjainak behatolását a szigetelőbe, a mobilis és a lokalizált elektronrendszer - Little modelljével [3] ellentétben - nem válik szét a térben. A Ginzburg modellt Allender, Bray és Bardeen részletesen tanulmányozta [12], egyetlen vezető ill. szigetelő réteg feltételezésével. Arra a következtetésre jutottak, hogy egy ilyen rendszerben a magashőmérsékletű szupravezetés meglehetősen valószínű.
Collins és munkatársai [13] sávszerkezeti számításokon [14] alapuló exciton-szupravezetés modellt dolgoztak ki CuCl és CdS kristályokra, hogy ezzel leírják az ezekben az anyagokban kísérletileg talált diamágneses anomáliát, amely a vezetőképességben mérhető nagy ugrással is együtt jár (a kísérleti eredményeket lásd a [13] irodalomban található hivatkozásokban). E modell szerint a Cu és Cd d-elektronjai egy keskeny betöltött sávot alkotnak, a Fermi szint pedig a Cl ill. S 3p-elektronjai által kialakított széles sávban fekszik. (Ez az eredetileg üres széles vezetési sáv részlegesen betöltötté válik a CuCl-ben található
![]() ill. a CdS-ben lévő
ill. a CdS-ben lévő
![]() szennyezések nyomás által ionizált elektronjainak megjelenésével.) Az általánosított Eliashberg egyenleteket [15] (Nambu formalizmus [16]) felhasználó modell számítások azt mutatják, hogy kritikus szennyezési koncentrációk mellett (amelyek a Fermi szint helyzetét határozzák meg) és a tiltott sáv értékének kritikus tartományainál szupravezető állapot jöhet létre, elsősorban triplett párok kialakulása következtében. Figyeljük meg, hogy ez az úgynevezett "keskeny sáv - széles sáv exciton" modell tulajdonképpen a rétegezett rendszerek
szennyezések nyomás által ionizált elektronjainak megjelenésével.) Az általánosított Eliashberg egyenleteket [15] (Nambu formalizmus [16]) felhasználó modell számítások azt mutatják, hogy kritikus szennyezési koncentrációk mellett (amelyek a Fermi szint helyzetét határozzák meg) és a tiltott sáv értékének kritikus tartományainál szupravezető állapot jöhet létre, elsősorban triplett párok kialakulása következtében. Figyeljük meg, hogy ez az úgynevezett "keskeny sáv - széles sáv exciton" modell tulajdonképpen a rétegezett rendszerek
![]() exciton szupravezetés elméletének [6, 7, 9] egy variánsa. Jóllehet az elmélet szerint igen valószínű, hogy a szupravezető állapot jelen van a CuCI és CdS rendszerekben, a tudományos közvélemény mégsem fogadta el ezt a következtetést, mivel a rosszul definiált szennyezési koncentrációk következtében a kísérletek nem voltak jól reprodukálhatóak.
exciton szupravezetés elméletének [6, 7, 9] egy variánsa. Jóllehet az elmélet szerint igen valószínű, hogy a szupravezető állapot jelen van a CuCI és CdS rendszerekben, a tudományos közvélemény mégsem fogadta el ezt a következtetést, mivel a rosszul definiált szennyezési koncentrációk következtében a kísérletek nem voltak jól reprodukálhatóak.
Magashőmérsékletű kerámia szupravezetők
Amikor Bednorz és Müller 1986-ban, kísérletileg szupravezetést fedezett fel
![]() 30- 40 K környékén a La2-xSrxCuO4 anyagokban [17], majd pedig Chu csoportja 1987-ben
30- 40 K környékén a La2-xSrxCuO4 anyagokban [17], majd pedig Chu csoportja 1987-ben
![]() 90-100 K-nál az Y Ba2Cu3O7 összetételű ún. "1 2 3 vegyületben" [18], minden előzetes elméleti feltételezés ellenére nagy meglepetés érte a fizikus társadalmat. Ezután olyan Bi és Tl tartalmú vegyületeket is felfedeztek, amelyek kritikus hőmérséklete elérte a 107 ill. 120 K-t [19].
90-100 K-nál az Y Ba2Cu3O7 összetételű ún. "1 2 3 vegyületben" [18], minden előzetes elméleti feltételezés ellenére nagy meglepetés érte a fizikus társadalmat. Ezután olyan Bi és Tl tartalmú vegyületeket is felfedeztek, amelyek kritikus hőmérséklete elérte a 107 ill. 120 K-t [19].
Amint azonban röntgen diffrakciós vizsgálatokkal kimutatták, az összes fenn említett bonyolult keramikus anyagnak közös tulajdonsága az, hogy olyan Cu-O síkokat tartalmaznak, ahol a kétféle atom tetragonálisan helyezkedik el. A kristályszerkezeti vizsgálatokon túlmenően igen sok más kísérlettel is tanulmányozták ezeket az anyagokat.
Az utóbbi két és fél évben nagyszámú elméleti modellt is felállítottak. Anélkül, hogy részletekbe mennénk, néhányat említünk ezek közül: Anderson és munkatársai rezonáló vegyértékkötés elmélete [20], Schrieffer és munkatársai spin-csomag modellje [21], Kresin plazmon-modellje [22], valamint szupravezetés kialakulása főként taszító elektron-elektron kölcsönhatás fluktuációk és gyenge retardált vonzó kölcsönhatás következtében (Zimányi és munkatársai [23]). Olyan modellek is léteznek továbbá, amelyek fononok vagy rezgési bi-polaronok vezető szerepét feltételezik (lásd pl. Yamaguchi és munkatársai [24]), Tachibana rezgési kölcsönhatásokra épülő modellje [25] és a mágneses (spin-polaron) elméletek különböző formái [26, 27]. Végül pedig a magashőmérsékletű szupravezetésnek vannak olyan elméletei is, amelyek az exciton mechanizmuson [28], vagy pedig általánosabban egy keskeny sáv elektronjainak polarizálhatóságán és egy széles sáv elektronjainak mozgékonyságán alapulnak [29].
Egy nemrégiben megjelent cikkében [30] Little - elemezve a legfontosabb kísérleteket - arra a következtetésre jutott, hogy a kerámia anyagokban fellépő szupravezetést gyengén csatolt szingulett, s-állapotú Cooper elektron- vagy lyukpárok okozzák, és így a BCS elmélet [3] itt is alkalmazható. A csatolás szerinte egy olyan exciton-mechanizmusból ered, amely a lokalizált d-elektronoknak egy széles sávban elhelyezkedő mozgékony oxigén 2p-elektronok által kiváltott polarizációjára épül. Tehát Little modellje és az, amit mi javasoltunk a CuCl és CdS vegyületekre, [14] valamint kerámia anyagokra [29] meglehetősen hasonlóak. Hangsúlyozni kell azonban, hogy legalábbis az 1 2 3 vegyület esetében az exciton spektrum létezésének kérdése ellentmondásos [31]. Másrészt a valódi excitonok hiánya nem változtatná lényegesen az alapvető következtetéseket, ugyanis a lokalizált elektronok polarizációjának leírása virtuális excitonok segítségével annak a képnek felel meg, amelyet a polarizációs propagátor elsőrendű diagrammjaiból származtathatunk. Excitonok hiányában a polarizáció másodrendű kifejezésekkel írható le [32]. Idézett cikkében [30] Little kizárja a mágneses effektusokat ("spin-polaronok"), de érvelése ezen a ponton kérdésesnek tűnik [26]. Könnyen elképzelhető, hogy a párképződés a keramikus anyagokban lényegében két különböző hatás eredménye: (1) a keskeny Cu d-sáv elektronjainak polarizációja és (2) mágneses excitonok (spin-polaronok) következménye [26].
Az irodalomban több sávszerkezet számolást is találunk lokális sűrűségfunkcionál közelítésben (LDA) a La2-xBaxCuO4 [33] és a Ca2Bi2Sr2Cu2O8 [34] kerámia anyagokra. A fenti rendszerekre linearizált APW számítást is végeztek [35]. Guo, Langlois és Goddard [36] az általánosított vegyérték sáv (GVB) modellt alkalmazta az Y Ba2Cu3O7-re. Véleményünk szerint meglehetősen kérdéses, hogy a szokásos szilárdtestfizikai módszerek, mint a lokális sűrűségfunkcionál közelítés vagy az APW, amelyek végül is az elektrongáz elképzelésen alapulnak, alkalmazhatók-e olyan rendszerekre, amelyek négy vagy öt különböző (könnyű és nehéz) atomfajtát tartalmaznak, kis és nagy elektron sűrűségek egyaránt előfordulnak, valamint a sűrűséggradiensek is nagyok. Guo, Langlois és Goddard számításai realisztikusabbnak tűnnek, de módszerük - amely nagyrészt figyelembe veszi az elektronkorrelációt is - rendkívül munkaigényes, mivel minden egyes sávra külön számolást kell elvégezni.
Klaszter- és sávszerkezet számítások
A fent említett okok miatt kezdtünk el a kerámia anyagok elektronszerkezetének kvantumkémiai meghatározásával foglalkozni. Ab iníció SCF LCAO kristálypálya (CO) számítást végeztünk nem-lokális kicserélődés figyelembevételével [37] (Cu-O)x és (Cu-O-Cu-O)x láncokra (az utóbbi esetben a "különböző pályák különbőző spinekre - DODS" formalizmust alkalmaztuk), valamint a kétdimenziós (Cu-O2)x síkra is. A fenti számításoknál az ún. kettős-zeta atomi bázisfüggvényeket [38] használtuk; a részletek több korábbi cikkünkben [37] megtalálhatók. Egydimenziós esetben a Fermi szint egy keskeny sáv közepén helyezkedik el (lásd az 1. ábrát), két dimenzióban azonban ez a sáv az oxigén 2pz pályái miatt meglehetősen szélessé válik (2. ábra.) míg a betöltött d sávok elég keskenyek.
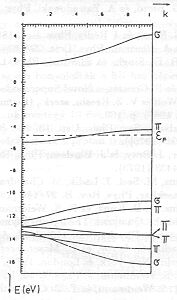
1. ábra A (Cu-O)x lánc ab iníció SCF LCAO sávszerkezete kettős-zeta atomi bázisfüggvényekkel [38].
Ez a típusú sávszerkezet láthatóan egyezik a fent említett "keskeny sáv - széles sáv modellel". Ha a számításokat egy kettős elemi cellával rendelkező láncra végezzük el, az oxigén atomokon váltakozó előjellel 1 és -1 spinsűrűség adódik, míg a réz atomokon a spinsűrűség nulla. A számítások így a kísérletekkel megegyezően alátámasztották a Cu-O lánc antiferromágneses viselkedését, a párosítatlan spinek azonban az oxigén atomokon helyezkednek el, nem pedig a rézen (lásd az 1. táblázatot is).
|
1. táblázat |
||||
|
"Különbözö pályák különböző spinekre" (DODS) sávszerkezeti számítás a (Cu1-O1-Cu2-O2)x láncra. Töltés és spin sűrűségek. |
||||
|
|
|
|
|
|
|
Cu1 |
14,087 |
14,088 |
-0,001 |
28,175 |
|
O1 |
3,908 |
4,926 |
-1,018 |
8,834 |
|
Cu2 |
4,082 |
14,082 |
0,000 |
28,164 |
|
O2 |
4,923 |
3,903 |
+1,020 |
8,826 |
Hasonló DODS számításokat végzünk jelenleg a kétdimenziós
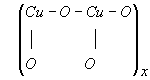
rendszerre, hogy kiderítsük, a párosítatlan spinek vajon ebben az esetben is az oxigén atomokon találhatók-e.
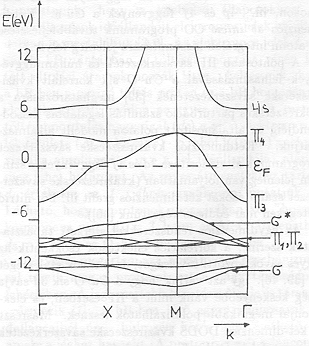
2. ábra A (Cu-O2)x sík kétdimenziós sávszerkezete ab iníció SCF LCAO kristály pálya módszerrel, kettős-zeta atomi bázisfüggvényeket használva. A
![]() sáv a nem-kötő (O12pz - O22pz) pálya következménye,
sáv a nem-kötő (O12pz - O22pz) pálya következménye,
![]() pedig a megfelelő (O12pz + O22pz) kötő pályából származik. A
pedig a megfelelő (O12pz + O22pz) kötő pályából származik. A
![]() sávokat lényegében a Cu 3dxz és 3dyz pályák határozzák meg, míg a
sávokat lényegében a Cu 3dxz és 3dyz pályák határozzák meg, míg a
![]() sávok a Cu
sávok a Cu
![]() és az O 2px ill. O 2py kötő ill. nem kötő kombinációinak felel
meg.
és az O 2px ill. O 2py kötő ill. nem kötő kombinációinak felel
meg.
Az eddig végzett számítások azonban még több szempontból is hiányosak. Először is, a tanulmányozott rendszernek megfelelő teljes kristály Madelung potenciálját figyelembe kell venni. A CuO5 rendszerre végzett ab iníció számítás, amelyet a Cu-O sík fölött elhelyezett négy 2+ ponttöltés jelenlétében ill. anélkül végeztünk el, azt mutatja, hogy a Madelung potenciál legvalószínűbb hatása az, hogy felcseréli a
![]() és
és ![]() sávok helyzetét (3. ábra.) Mivel azonban a
sávok helyzetét (3. ábra.) Mivel azonban a
![]() sáv is lényegesen szélesebb a réz 3d sávjainál, ez a tény nem változtatja meg a szupravezetés "két sáv modelljének" érvényességére vonatkozó következtetéseket.
sáv is lényegesen szélesebb a réz 3d sávjainál, ez a tény nem változtatja meg a szupravezetés "két sáv modelljének" érvényességére vonatkozó következtetéseket.
Megemlítjük még, hogy a Madelung potenciál korrekt meghatározására az adott kerámia anyagokban jelenleg klaszter számolásokat végzünk, ahol a Cu és O atomok mellett La, Z, Ba, Sr, Bi és Td atomokat is figyelembe veszünk. A számításokból meghatározható lesz a Cu-O sík és a többi atomsíkok közötti töltésátvitel is. Így azon kívül, hogy megkapjuk a Madelung potenciál kiszámításához szükséges pontos töltés értékeket, lehetőség van arra is, hogy a nagy valószínűség szerint nem semleges Cu-O sík energiasávjait megfelelően betölthessük.
Ahhoz, hogy figyelembe vehessük a korreláció sávszerkezetre gyakorolt hatásának nagy részét, a két dimenziós Hartree-Fock (HF) kristály pálya számításokat meg kell ismételni ún. polarizációs függvények alkalmazásával is. (Ezek a 3d függvények az O atomokon, ill. 4p és 4f függvények a Cu-n. Kétdimenziós ab iníció CO programunk továbbfejlesztése f atomi integrálok kiszámítására jelenleg folyik.)
A pontosabb HF sávszerkezetek és hullámfüggvények felhasználásával a Cu-O sík korrelált kvázirészecske sávszerkezetének [39] meghatározására a sokrészecskés perturbáció számítás legalábbis másodrendjéig az általánosított polaron modellt alkalmazhatjuk. Kétdimenziós kvázirészecske sávszerkezet programunk általánosítása 3d és 4f függvényekre szintén jelenleg van folyamatban (kvázirészecske sávszerkezet számításokat két dimenziós grafit ill. bór-nitrid rétegeken már eddig is végeztünk [40]).
Az egydimenziós rendszerekkel szerzett tapasztalatok szerint, a korrelációs effektusok csökkentik az egyes sávok közötti távolságot, de a sávok szélességét is [39, 40]. Így azt várjuk, hogy a Cu-O sík 3d sávja még keskenyebbé válik mint a HF esetben, és elektronjai méginkább polarizálhatók lesznek. Másrészt a két-dimenziós DODS kvázirészecske sávszerkezetek és a megfelelő hullámfüggvények (az ehhez szükséges elméleti módszert már kidolgoztuk, a programozási munka pedig most folyik) fogják megadni a választ arra a kérdésre, hogy a spin-polaron mechanizmus [26, 27] valóban fontos szerepet játszik-e a kerámia anyagok magashőmérsékletű szupravezetésében. Ehhez meg kell oldanunk a BCS gap egyenleteket és meghatároznunk Tc-t, először a "két sáv modell" és a spin-polaron mechanizmus érvényességét külön-külön feltételezve, majd pedig mindkettőjük szerepét egyszerre tanulmányozva.
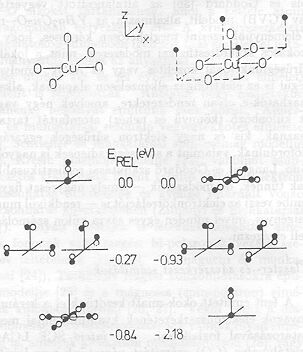
3. ábra A CuO5 klaszter energia szintjei a Cu-O sík fölött elhelyezett négy 2+ ponttöltés jelenlétében és anélkül. A Cu-O távolsága a síkban 1,94 Ǻ, a sík feletti oxigén atom és a réz távolsága 2,38 Ǻ; végül pedig a ponttöltések és a Cu-O sík távolságát 1,99 Ǻ -nek
választottuk.
IRODALOM
[1] F. London, Superfluids (Wiley, New Tork, 1950), Vol. I.
[2] W. A. Little, Phys. Rev. 134A, 1416 (1964).
[3] J. Bardeen, L. N. Cooper, és J. R. Schrieffer, Phys Rev. 108, 1175 (1957).
[4] R. A. Ferrell, Phys. Rev. Lett. 13, 330 (1964).
[5] W. A. Little, Phys. Rev. 156, 396 (1967).
[6] J. Ladik, G. Biczó, és A. Zawadowski, Phys. Lett. 18, 257 (1965).
[7] J. Ladik, G. Biczó, és J. Rédly, Phys. Rev. 188, 710 (1969).
[8] J. Ladik és A. Bierman, Phys. Lett. 29A,636 (1969).
[9] J. Ladik, R. D. Singh, és S. Suhai, Phys. Lett 81A, 488 (1981).
[10] D. Jérome és F. Creuzet, a Novel Superconductivity kötetben, S. A. Wolf és V. Z. Kresin, szerk., (Plenum, New York és London, 1987), p. 103.
[11] V. L. Ginzburg, Sov. Phys. Usp. 13, 335 (1970) (JETP Lett. 14, 393 (1970)).
[12] D. Allender, J. Bray, és J. Bardeen, Phys. Rev. B 7, 1020 (1973); 8, 4433 (1973).
[13] T. C. Collins, M. Seel, J. Ladik, M. Chandrasekhar, és H. P. Chandrasekhar, Phys, Rev. B. 27, 140 (1983).
[14] T. C. Collins, A. B. Kunz, és R. S. Weidmann, an Recent Advances in the Quantum Theory of Polymers kötetben, Lecture Notes in Physics, Vol. 113, J.-M. André, J. Delhalle, J. Ladik, G. Leroy, és C. Moser, szerk. (Springer-Verflag, Berlin, New York, és London, 1979), p. 240; A. B. Kunz és R. S. Weidmann, J. Phys. C 12, L371 (1979); A. B. Kunz, R. S. Weidmann, és T. C. Collins, J. Phys. C 14, L581 (1981).
[15] G. Eliashberg, Sov. Phys. JETP 11, 696 (1960).
[16] Y. Nambu, Phys. Rev. 117, 648 (1960).
[17] J. G. Bednorz és K. A. Müller, Z. Phys. B64, 189 (1986).
[18] C. W. Chu, P. H. Hor, R. L. Meng, L. Gao, Z. J. Huang, és Y. O. Wang, Phys. Rev. Lett. 58, 405 (1987); P. H. Hor, R. L. Meng, Y. O. Wang, L. Gao, Z. J. Huang, J. Bechtold, K. Forster, és C. W. Chu, Pliys. Rev. Lett. 58, 1891 (1987).
[19] R. Dogani, Science, May 16, 24 (1988).
[20] P. W. Anderson, G. Baskaranu, Z. Zou, és T. Hsu, Phys. Rev. Lett 58, 2790 (1987).
[21] J. R. Schrieffer, X.-G. Wen, és S.-C. Zhang, Phys. Rev. Lett. 60, 944 (1988).
[22] V. Z. Kresin, Phys. Rev. B 35, 8716 (1987).
[23] G. T. Zimányi, S. A. Kivelson, és A. Luther, Phys. Rev. Lett, 60, 2087 (1988).
[24] K. Yamaguchi, Y. Takahara, T. Fueno, és K. Nasu, Jap. J. Appl, Phys. 26. 2037 (1987).
[25] A. Tachibana. Phys. Rev. A 35, 18 (1987).
[26] R. F. Wood, Phys. Rev. B, közlésre beküldve.
[27] G. Chen és W. A. Goddard III, Science 239, 899 (1988) ; H. Kamimura, S. Matsumo, és R. Saito, Solid Statae Commun, 67, 363 (1988); V. J. Emery és G. Reitter, Phys. Rev. B 38, 4547 (1988).
[28] W. A. Little, a Novel Superconductivity kötetben, S. A. Wolf és V. Z. Kresin, szerk. (Plenum, New York és London, 1987), p. 341; A. Zawadowski, Phys. Rev. B, megjelenés alatt; M. Jarell, H. R. Krishannuty, és D. L. Cox. Phys. Rev. B 38, 4584 (1988).
[29] J. J. Ladik és T. C. Collins, a Novel Superconductivity kötetben S. A. Wolf és V. Z. Kresin, szerk. (Plenum, New York és London, 1987), p. 181; T. C. Collins, A. B. Kunz, és J. J. Ladik, ugyanott, p. 378.
[30] W. A. Little, Science 242, 1390 (1988).
[31] I. Bozovic, D. Kirillov, A. Kapitulnik, K. Char, M. R. Hahn, M. R. Bedsley, T. H. Geballe, Y. H. Kim, és A. J. Heeger, Phys. Rev Lett. 59, 2219 (1987).
[32] A. L. Fetter és J. D. Walecka, Quantum Theory of Many-Particle Systems (McGraw-Hill, New York, 1971), p. 558.
[33] J. Yu, A. J. Freeman, és J.-H. Ku, Phys. Rev. Lett. 58, 1035 (1987).
[34] M. S. Hybertsen és L. F. Mattheis, Phys. Rev. Lett. 60, 1661 (1988).
[35] F. Mattheis, Phys. Rev. Lett 58, 1028 (1987).
[36] Y. Guo, J.-M. Langlois, és W. Goddard, Science 239, 896 (1988).
[37] G. Del Re, J. Ladik és G. Biczó, Phys. Rev. 155, 997 (1967); J.-M. André, L. Gouverneur, és G. Leroy, Int. J. Quant, Chem. 1, 427,451 (1967); P. Saalfrank, J. Ladik, és R. F. Wood, Phys. Rev. B, megjelenés alatt.
[38] (a) O-ra ((9s5p)/(4s2p)): T. H. Dunning és P. J. Hay, a Modern Theoretical Chemistry kötetben, H. F. Schaeffer III, szerk. (Plenum, New York és London, 1977), Vol. 3, p. 1; (b) Cu-ra ((14s8p5d/(8s4p2d)) 2D állapotra optimalizálva: S. Huzinaga, a Physical Science Data 16, Gaussian Basis Sets for Molecular Calculations kötetben, S. Huzinaga, szerk. (Elsevier, New York, 1985), p. 192.
[39] S. Suhai, Phys. Rev. B 27, 3506 (1983).
[40] M. Vracko, C.-M. Liegener, és J. Ladik, Chem. Phys. Lett., megjelenés alatt; Int. J. Quant. Chem., megjelenés alatt.
[41] C.-M. Liegener, J. Phys. C 18, 6011 (1985); C.-M. Liegener és J. Ladik, Chem. Phys. 106, 1339 (1986); C.-M. Liegener, J. Chem. Phys., megjelenés alatt.
[42] C.-M. Liegener és J. Ladik, publikálatlan eredmények.
________________________
Fordította: Pipek János, BME Fizikai Intézet