A HŐMÉRSÉKLET FOGALMA

Kürti Miklós
Clarendon Laboratórium, Oxford

Ez a hangzatos cím a "hőmérséklet fogalma" valójában nem azt jelenti, hogy új érdekes gondolatokat akarok előadnia hőmérséklet fogalmával kapcsolatban. Csak azt szeretném elmondani, hogy hogyan próbáltam bizonyos fogalmakat megérteni és általam ésszerűnek tartott módon másoknak elmagyarázni. Kezdjük először is azzal, hogy mi is a hőmérséklet. Mi a hőmérséklet definíciója?

Eszembe jut egy jelenet, ami 1920-ban Párizsban egy szóbeli vizsgán játszódott le. A szóbeli vizsgák mindig egy nagy előadóteremben folytak. A hallgatók mind ott ültek, és felkészülés gyanánt figyelték, hogy milyen kérdéseket tesznek fel. A professzor azt kérte a vizsgázótól, hogy definiálja a hőmérsékletet. Nos, a hallgató azt válaszolta, hogy

Hát a diák gondolkodott megint, eszébe jutott a Carnot-féle definíció, és azt mondta:

- A hőmérséklet az a fogalom, ami lehelővé teszi kél hőforrás között működő hőerőgép ideális halásjokának meghatározását.

- mais non, mais non! - a tanár már nagyon nagyon dühös volt.

Végül a diáknak eszébe jutott a második főtétel Caratheodory féle matematikai megfogalmazása:

- Az abszolút hőmérséklet reciproka az az integráló lényező, ami a hőmennyiségből egy teljes differenciált képez, amit entrópiának nevezünk.

- mais non, mais non! - mondta a professzor, és felállt.

(A hőmérséklet csak egy érzés, egy érzéki percepció.) És ez valóban így is van. Ha az ember megnézi a különböző szótárakat, látja, hogy ez a hőmérséklet eredeti definíciója. Például a hőmérséklet angol szótári definíciója a következő: A hőmérséklet az érzékelhető meleg mértéke, amint azt az ember érintés útján érzékeli, vagy ahogy különböző anyagok tulajdonságainak megváltozásában megnyilvánul, és ezen megváltozások segítségével hőmérők készíthetők.

(Megj. Az Új Magyar Lexikon definíciója: Fizikailag az anyag makroszkopikus állapotát jellemző állapothatározók egyike. Fogalmát és a különböző hőmérsékleti skálákat a különféle anyagok érintésekor az emberekben kialakuló hideg-, meleg-, langyos stb. szubjektív érzetek pontossá tételére, objektív megjelölésére vezették be.)

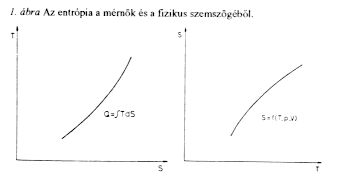
Lépjünk egy kicsit tovább! Nyilvánvalóan a hőmérséklet-fogalom különböző emberek számára különböző- A fizikus egy kicsit másként tekint a hőmérsékletre, mint a mérnök. Előfordul, hogy beszélünk valakivel, és ki akarjuk deríteni - anélkül, hogy rákérdeznénk - hogy mérnök-e vagy fizikus vagy vegyész. Csak annyit kell tennünk, hogy a termodinamikára tereljük a szót. Ezután csak arra kell kérnünk, hogy rajzoljon fel egy T-S diagramot (l. ábra). Ha fizikust vagy kémikust kérdezünk, akkor az mindig úgy rajzolja fel a görbét, hogy az entrópia az ordináta és a hőmérséklet az abszcissza. A fizikus, a vegyész és a statisztikus mechanikus ugyanis az entrópiát egy olyan függvénynek tekinti, amely, meghatározza egy anyag állapotát, tehát az entrópia bizonyos dolgok függvénye, és általában ez a standard definíció. Ha azonban egy mérnököt kérdezünk meg, ő T-t mindig mint az S függvényét fogja ábrázolni. Ennek az az oka, hogy a mérnököt nem nagyon érdekli az entrópia fogalma. Számára az entrópia egy nagyon gyakorlati dolog: A hőmennyiség nem más, mint a hőmérséklet és az entrópia megváltozás szorzatának az integrálja. Már pedig, ha valamit integrálunk, mindig a vízszintes tengelyen lévő változó szerint integrálunk, és nem fordítva. Ez az oka annak, hogy a mérnök mindig T(S) és nem S(T) diagramot rajzol. Ez a legegyszerűbb mód arra, hogy megkülönböztessünk egy mérnököt egy fizikustól.

Hogyan vezetjük be az iskolában vagy az egyetemen az abszolút hőmérsékleti skálát? Veszünk egy gázhőmérőt, azaz egy gázzal töltött edényt. Megmérjük a gáz nyomását, mint valami kvantitatív skála függvényét. Majd azt mondjuk: Tegyük fel, hogy a víz forráspontján ennyi a nyomás, a jég olvadáspontján pedig ennyi *. A két pontot egy egyenessel összekötjük, és száz egyenlő részre osztjuk. Így megkapjuk a Celsius skálát (2. ábra).

Egyszer egy nagyon kellemetlen élményben volt részem. Néhány másodpercig nagyon tanácstalannak éreztem magamat egy csoport fizikatanár előtt.

A nagyon alacsony hőmérsékletekről beszéltem. Megemlítettem nekik, hogy a hőmérsékletet néhány K pontossággal tudjuk mérni. Nagyon, nagyon alacsony hőmérsékleten alkalmazhatjuk a termodinamika második főtételét mágneses anyagokra, és nagyon nagy pontossággal mondhatjuk ez 3 K, ez 4 K stb. Valaki a hallgatóságból megkérdezte tőlem:

Egy pillanatra megdöbbentem. Azután eszembe jutott, hogy természetesen a gond, illetve a magyarázat abban rejlik, hogy a termodinamikai hőmérsékleteket mindig, mint arányokat definiáljuk, sohasem különbségekként. Ez fontos, amit meg kell jegyezni. Amíg magas hőmérsékleteknél egy nagyon kis hőmérséklet tartományban dolgozunk, ez nem jelent nagy különbséget. Alacsony hőmérsékleteknél azonban nem szabad elfelejteni, hogy csak a hőmérséklet arányok számítanak. Most megadom a korrekt definíciót. Elvileg elvégezhetünk egy hőgép kísérletet a jég olvadáspontja és a víz forráspontja között. Valójában ezt nagyon gyakran tesszük. Mérjük a térfogat, nyomás, hőmérséklet értékeit, a gáz fajhőjét, a folyadék fajhőjét, a párolgási hőt, stb., mindent, ami a hatásfok számításhoz szükséges. Kísérleti úton azt kapjuk, hogy a forrásponthoz és az olvadásponthoz tartozó abszolút hőmérséklet aránya 1,36609. Ha posztuláljuk, hogy a forrásponti hőmérséklet és az olvadásponthoz tartozó hőmérséklet különbsége legyen 100 egység, akkor az olvadáspánt hőmérséklete 273,15 lesz. A 273,15 K-t 0,00000 °C-nak is definiálhatjuk.

Nagyon fontos, hogy a diákoknak megtanítsuk, hogy a termodinamika a hőmérsékletarányokat rögzíti.

Menjünk egy lépéssel tovább. Térjünk vissza újra a gázhőmérőhöz. Az ideális gáz nyomása állandó térfogatnál arányos az abszolút hőmérséklettel. Ez az energia ekvipartíció-törvényével függ össze. Hogyan kapjuk meg az ekvipartíció törvényét? Az ekvipartíció törvényéhez három fontos feltevést kell tennünk:

- A rendszer energiája a változók homogén másodrendű függvénye. Egy molekula vagy atom először is rendelkezik kinetikus energiával, ami természetesen a sebességek négyzetével arányos, és potenciális energiával, ami az elmozdulások négyzetével arányos.

- Ha most ki akarjuk számítani a részecske rendszer átlagos energiáját, akkor feltételezzük, hogy az energia folytonosan változik. Minden szabadságfokhoz, azaz a Hamilton-függvény minden négyzetes változójához 1/2 kT energia tartozik.

- Az energia korlátos.

Nézzük, most a feltételeket, hogy valóban teljesülnek-e?

Az elméletből következik, hogy szilárd testek atomhője 6 kalória/szabadságfok. Régóta tudjuk, hogy ha a hőmérséklet elég magas, akkor ez már nem igaz. Ennek elsősorban az az oka, hogy amikor magas hőmérsékleten az elmozdulások nagyon nagyok, akkor a négyzetes energiatörvény többé már nem érvényes, a részecske Hamilton-függvényében harmadfokú tag is fellép, így a fajhő növekszik.

Alacsony hőmérsékleten a kvantálás miatt az a feltétel sem teljesut, hogy az energia a paraméterek folytonos függvénye. Ez viszont azt eredményezi, hogy a fajhő alacsony hőmérsékleten csökken.

Nézzük a következő kérdést! Valóban igaz-e, hogy minden rendszerben korlátos az energia? A rendszer valóban csak annyi energiát tud elnyelni, amennyi még változást tud benne előidézni?

Igen is és nem is. Tekintsünk egy nagyon egyszerű rendszert: Külső mágneses térben elhelyezett spint. A spin a mágneses térhez képest parallel illetve antiparallel állhat be, az energiakülönbség arányos a mágneses térrel. Abszolút zérus hőmérsékleten minden részecske az alsó energiaszinten helyezkedik el. Ha több energiát pumpálunk a rendszerbe, akkor egyre több részecske kerül át a felső tartományba. Végül egy bizonyos ponton kialakul a rendszerben az egyenletes energia eloszlás, ugyanannyi lesz fönt, mint lent (3. ábra).

Nézzük meg, hogy milyen termodinamikai függvényei vannak egy ilyen részecske-rendszernek. Az entrópia az alapállapottól függően nulláról indul, illetve konstansról, ha az alapállapot degenerált. Majd növekszik abban a hőmérséklet tartományban, ahol a részecskék a magasabb energia szintre kerülnek fel. Végül eléri az egyenlet által megadott maximális értéket. Az energia egy hasonló függvény. A fajhőt a szokásos jól ismert Schottky fajhőgörbe jellemzi. , ahol k a Boltzmann állandó, és az energiakülönbség). A fajhő növekszik, majd elér egy maximális értéket. Ezután csökkenni kezd, majd nagyon nagy hőmérsékleten az izoláltspin-rendszer fajhője zérussá válik (4. ábra).

A következő példának nem csak történeti érdekessége van. Ez az első példa arra, hogy a fajhő mérés lehetővé tette az energiaszintek szétválasztását. Egy fajhőmérő eszközről van szó, amit 1931-ben Berlinben készítettem gadolíniumszulfát fajhőjének mérésére (5. ábra). A gadolíniumszulfát egy nyolc energiaszinttel rendelkező mágneses anyag. Ezt az anyagot javasolták a mágneses hűtés megvalósításához. Magas hőmérsékleten a spinrendszer nem járul hozzá a fajhöhöz. Azt teljesen meghatározza a fajhő Debye-görbéje, mivel mint tudjuk, a spinrendszer fajhője nagy hőmérsékleten nulla. Ha azonban olyan alacsony hőmérsékletén dolgozunk, ahol a rács fajhő gyorsan csökken, akkor detektálni és tanulmányozni tudjuk a spinfajhő növekedését alacsony hőmérsékleten. Ennek a görbének a segítségével meg tudtuk előre becsülni, hogy milyen hőmérséklet lesz elérhető a mágneses hűtőrendszerrel. És a becslések valóban elég jók voltak. Ez egy példa arra, hogy a fajhő meghatározás hogyan teszi lehetővé bizonyos összetett anyagok energiakülönbségeinek mérését.

Térjünk most vissza az izolált spinrendszer kérdésére. Ha azt mondjuk, hogy egy spinrendszer izolált, akkor ez egy szép absztrakció, azonban egy magspin-rendszert nem lehet elszigetelni a környezetétől. A magspinek kölcsönhatnak az atom elektronjaival, ezek pedig a rácsrezgések fononj aival.

Lehetetlen azt mondani, hogy ez a rendszer izolált. Azt könnyen el tudjuk képzelni, hogy egy anyag egy másiktól el van szigetelve, például vákuummal vagy valamilyen megfelelő anyaggal. Ha azonban egy olyan rendszert tekintünk, ami bele van ágyazva a másik rendszerbe, azt hogyan tudjuk elszigeteltnek tekinteni? A következő egyszerű példa segítségével megpróbálom megmagyarázni, hogy ez lehetséges.

Képzeljünk el egy futballmeccset például a Fradi és az Arsenal között. Tegyük fel, hogy a magyar csapat győz. A meccs után rendeznek egy koktélpartit, amelyen részt vesznek a magyarok és a szurkolóik, valamint az angolok és a szurkolóik. Teljesen összekeverve egy szobában. Valóságosan össze vannak keverve! A magyarok és az angolok nincsenek szétválasztva. A magyarok azonban nem beszélnek angolul, és az angolok nem beszélnek magyarul. Beszélnek egymáshoz, a magyarok a magyarokhoz, az angolok az angolokhoz, de a csoportok nem értik egymást. Van tehát két olyan rendszerünk, ami össze is van egymással keveredve, mégis el van választva. Nem tudnak egymással kommunikálni. A képen látjuk az angolokat. Nagyon szomorúak, levertek, mivel elvesztették a mérkőzést. A magyarok mosolyognak. A két rendszer össze van keveredve, de különböző hangulatban vannak. Különböző a hőmérsékletük. A magyarok forrók, az angolok hidegek. Mi történik ezután? Ez örökre így marad? Nem. Mint tudjuk, a hangulat ragadós. Így egy bizonyos idő után a magyarok nagy vidámsága lassan hatni kezd az angolokra. Kezdenek egy kicsit kevésbé letörtek lenni. A magyarok kitörő vidámsága is egy kicsit alábbhagy, amint látják a szomorú legyőzött angolokat. Egy kicsit mérsékeltebbé válik az ujjongásuk. Így lassan kiegyenlítődik a hangulat, kiegyenlítődik a hőmérséklet. Ennek a kiegyenlítődésnek az időállandóját relaxációs időnek nevezzük. Bizonyos spinrendszerekben - különösen dielektromos anyagok esetében - ez a relaxációs idő különlegesen hosszú lehet. Órákig, napokig, vagy akár századokig is tarthat. Ha csökkenteni akarjuk a relaxációs időt, akkor ezt hagyományosan megtehetjük a paramágneses szennyeződés bevitelével. Hasonló a helyzet a koktélparti esetében, de itt a relaxációs idő az alkohol mennyiségének növelésével csökkenthető.

Meg van tehát az előírásunk arra, hogy hogyan tudunk létrehozni egy olyan spinrendszert, ami teljesen el van szigetelve a környezetétől, és hogyan tudjuk befolyásolni a környezettel való energiacserét. Most egy nagyon érdekes kérdéshez jutunk. Nézzük újra a 3. ábrát. Mi történik most? A két energiaszintű spinrendszerrel végtelen nagy hőmérsékletet értünk el. Feltételezzük, hogy a spinrendszer izolált. Ha energiát viszünk a rendszerbe, azt nem tudja átadni semmi másnak. Ha több energiát viszünk be, mint ami a végtelen hőmérséklet eléréséhez szükséges, akkor a felső energiaszint jobban be lesz töltve, mint az alsó, ami azt jelenti, hogy tekintettel a Boltzmann tényező alakjára:

,

ahhoz, hogy a felső energia szinten nagyobb betöltöttséget érjünk el, posztulálnunk kell egy negatív abszolút hőmérsékletet. Nézzük meg, hogy ez hogyan valósítható meg egy spinrendszerben! Hogyan vihetünk be még annál is több energiát a rendszerbe, hogy végtelen hőmérsékletű állapotba kerüljön? Majdnem azt mondanám, hogy mi sem egyszerűbb. Legalábbis Purcell és Pound számára nagyon egyszerű volt 30 évvel ezelőtt. Egy elvileg nagyon egyszerű, de megvalósítás szempontjából nagyon nehéz kísérletet végeztek. Vettek egy spinrendszert, pozitív hőmérsékleten, ezt mágneses térbe helyezték. Majd nagyon gyorsan, körülbelül 1 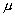s idő alatt megfordították a mágneses mező irányát. Olyan gyorsan, hogy a magspinek ne tudjanak átállni. Így a magspinek hirtelen a nagyobb energiájú tartományba kerültek, és ott is maradtak. Ez azt jelenti, hogy több energia került a rendszerbe, mint ami a végtelen hőmérsékletű állapot eléréséhez szükséges, így a hőmérséklet átváltott a negatív tartományba. Mi történik ezután? A spinrendszer nincs teljesen elválasztva a környezetétől, van egy lassú hőátadás. Mi történik hát? A negatív hömérséklet abszolút értéke növekedni kezd, azaz a spinrendszer hűl, míg végül el nem éri a végtelen hőmérsékletet. Másszóval, a negatív hőmérséklet a végtelen nagy hőmérsékletre fog lehűlni, majd átmegy a pozitív tartományba. Most egy nagyon tanulságos diagramot mutatok, ami Ramsaytől származik. Az entrópiát a rendszer energiájának függvényében ábrázolom. Induljunk ki a abszolút zérus pontból, ekkor minden részecske az alsó energiaszinten van. Most vigyünk be energiát a rendszerbe. Az entrópia növekedni fog, amíg el nem éri a végtelen nagy hőmérsékletnek megfelelő maximális entrópia értéket. Ezután pumpáljunk még több energiát a rendszerbe. Ekkor az entrópia újra csökkenni kezd, mivel most nem érvényes az egyenletes eloszlás, valamivel több részecske van a felső, mint az alsó energiaszinten. Végül eléitkezünk a negatív abszolút zérushoz. Tehát két abszolút zéruspont van. Ez egy nagyon tanulságos tény. Közönséges rendszerekben, melyeknek nem korlátos az energiaspektruma, érthető a végtelen nagy hőmérséklet. Izolált spinrendszerek esetében azonban a végtelen nagy hőmérséklet majdnem trivialitás. Ugyanis minden olyan anyag, ami egyszer már a negatív hőmérséklet-tartományba került, a lehűlés során szükségszerűen keresztülmegy a végtelen hőmérsékleten, hogy majd elérje a pozitív hőmérséklet tartományt (6. ábra).

E szerint az interpretáció szerint az abszolút zéruspont valójában a hőmérsékleti skála egy nagyon érdekes szingularitását jelenti. Ez kétértékű szingularitás. Létezhet olyan anyag, amelynek más más tulajdonságai vannak a pozitív és a negatív abszolút zérusponton. Ezzel kapcsolatban kollégáim (Lounasma csoportja) Finnországban egy gyönyörű kísérletet végeztek, melynek során fémekben vittek le spineket a rendezett állapotnak megfelelő átmeneti hőmérséklet alá. Úgy találták, hogy a pozitív abszolút zérusponton a rendszer ferromágneses, míg negatív abszolút zérusponton antiferromágneses. Sok még a rejtély, de sok dolgot meg lehet érteni, ha a bizonyos dolgokat posztulálunk. És úgy gondolom, hinniük kell abban, hogy a negatív abszolút hőmérséklet nem fikció, hanem realitás. Gyakorlati jelentősége azonban nincs.

Természetesen, ugyanúgy, ahogy el tudunk képzelni egy olyan világot, amelyet kizárólag antiprotonok, antineutrínók és pozitronok népesítenek be, el tudunk képzelni egy olyan világot is, amelyben a negatív hőmérsékletek az igazán fontosak. Talán bizonyos esetekben alsó korlátja is van az energiaszintnek. Ez azonban olyan spekuláció, amibe nem akarok belebonyolódni, és ezt Önöknek sem ajánlom.

__________________________