Fizikai Szemle honlap |
Tartalomjegyzék |
Szatmáry Zoltán
Budapesti Műszaki Egyetem
Nukleáris Technikai Intézet
Carlo Rubbia Nobel-díjas, az MTA tiszteletbeli tagja 1994. február 18-án tartott székfoglalójában felvetette egy spallációs neutronforrással kombinált tóriumos reaktor gondolatát, amelynek a segítségével úgy lehet villamos energiát termelni, hogy az atomerőművek számos ismert problémája nem merül fel. Az előadáson készült hangfelvétel és a CERN/AT/93-47 preprint alapján az előadást a Fizikai Szemle 1994. áprilisi száma közölte. Az alábbiakban ennek a közleménynek az alapján fűzünk néhány megjegyzést a javasolt megoldáshoz. Mindenekelőtt azonban összefoglaljuk a javaslat lényegét.
Egy szinkrotronban 1 GeV energiára gyorsított protonokat nehézfém (például ólom) targetra lőve spallációs reakció révén intenzív neutronforrást kapunk. A neutronok egy grafittal moderált és vízzel hűtött, tóriumot tartalmazó rendszerbe jutnak. A tórium-grafit fűtőelemek golyó alakúak. (Felépítésükre még visszatérünk.) A neutronok hatására a tóriumból 233U izotóp keletkezik, és a berendezésben ennek a hasadása révén termelődik energia. Ha megfelelően választjuk meg a rendszerben kialakuló neutronfluxus nagyságát, akkor a gyorsító által fogyasztott villamos energia sokszorosát kapjuk így vissza. Erre való tekintettel nevezte el rendszerét Rubbia energiasokszorozó rendszernek. Számítógépes modelljével végzett számítások szerint az 233U mennyisége hozzávetőleg l022n/cm2 értékű integrált neutronfluxus elérése után arányossá válik a 232Th (lassan csökkenő) mennyiségével. A két izotóp arányára a következő képletet adja meg:
(1)
![]()
ahol a 23 és 02 indexek rendre az 233U és 232Th izotópokat jelentik. A képletben szereplő hatáskeresztmetszetek termikus neutronspektrumra átlagolt értékek. (A reaktorfizikában megszokott jelölésmód szerint a nehéz izotópokat a rendszámuk és tömegszámuk utolsó számjegyével jelöljük.) Ez az arány független a fluxustól, és ezért Rubbia természeti állandónak minősíti. (1) szerint tehát, például, egy 5 tonna tóriumot tartalmazó rendszerben az 233U mennyisége 67 kg-ban stabilizálódik (ha a tóriumlassú fogyásától eltekintünk). A kapott hőteljesítmény ekkor arányos a ![]() neutronfluxussal. Az előbbi példában egy
neutronfluxussal. Az előbbi példában egy ![]() = 1,5
= 1,5
 1014 n/cm2s értékű termikus neutronfluxushoz 250 MW hőteljesítmény tartozik. 1014 n/cm2s-nál sokkal nagyobb neutronfluxust nem tart kívánatosnak, mert ilyen fluxus mellett túlságosan megnőne a 233Pa-ban befogódó neutronok száma, és ez rontaná az energiasokszorozó hatásfokát, amelyet a következőképpen definiál:
1014 n/cm2s értékű termikus neutronfluxushoz 250 MW hőteljesítmény tartozik. 1014 n/cm2s-nál sokkal nagyobb neutronfluxust nem tart kívánatosnak, mert ilyen fluxus mellett túlságosan megnőne a 233Pa-ban befogódó neutronok száma, és ez rontaná az energiasokszorozó hatásfokát, amelyet a következőképpen definiál:
(2)
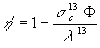
ahol ![]() a 233Pa magok bomlási állandója. (
a 233Pa magok bomlási állandója. (![]() -val a későbbiekben mást fogunk jelölni, ezért láttuk el a mostani
-val a későbbiekben mást fogunk jelölni, ezért láttuk el a mostani
![]() vesszővel.) A cikkben
vesszővel.) A cikkben ![]() helyett
helyett ![]() (a 233Pa magok átlagos élettartama) szerepel, ami nyilván elírás: (2)-ben a számlálót és nevezőt N13-mal szorozva a számláló a neutronbefogások, a nevező pedig a radioaktív bomlások másodpercenkénti számát adja meg. Ezek hányadosa dimenzió nélküli, amelyet értelmes levonni 1-ből. Ha azonban
(a 233Pa magok átlagos élettartama) szerepel, ami nyilván elírás: (2)-ben a számlálót és nevezőt N13-mal szorozva a számláló a neutronbefogások, a nevező pedig a radioaktív bomlások másodpercenkénti számát adja meg. Ezek hányadosa dimenzió nélküli, amelyet értelmes levonni 1-ből. Ha azonban ![]() , helyett
, helyett ![]() áll, akkor a (2) alatti tört számlálójának más a dimenziója, mint a nevezőnek (1/s illetve s), amivel a (2) képlet értelmetlen.
áll, akkor a (2) alatti tört számlálójának más a dimenziója, mint a nevezőnek (1/s illetve s), amivel a (2) képlet értelmetlen.
Rubbia a következőkben látja javasolt rendszerének a főbb előnyeit:
a) A rendszer szubkritikus, tehát a szabályozásra nincs szükség, továbbá kizárt a reaktivitásbaleset (megszaladás).
b) A folyamat nagyon kis mértékben vezet hosszú felezési idejű aktinidák keletkezésére, tehát az elhasznált üzemanyag tárolása kisebb gondot jelent, mint a szokványos atomerőművek esetében.
c) A berendezés a tórium teljes mennyiségét hasznosítja, tehát ez a rendszer elvileg évmilliókra megoldja az emberiség energiagondjait - szemben az urános rendszerekkel, amelyek esetében csak a 7 ezreléket kitevő 233U izotóp hasznosul.
d) A rendszer működése biztonságos, hiszen a gyorsító kikapcsolásakor az energiatermelés leáll. A rendszer stabil, hiszen az (1) képlettel adott izotóparánytól való (bármilyen előjelű) spontán eltérést követően az (1) alatti arányt egy negatív visszacsatolás automatikusan visszaállítja.
e) Mivel az 233U nagyenergiájú ![]() -sugárzást bocsát ki, az ilyen módon termelt hasadóanyagot a terroristák nem szívesen lopnák el bombakészítés céljából.
-sugárzást bocsát ki, az ilyen módon termelt hasadóanyagot a terroristák nem szívesen lopnák el bombakészítés céljából.
Végeredményben tehát a javasolt rendszerrel - szerző szerint - végre megoldódik a "ma és a közeljövő társadalmának sürgető központi kérdése, a tiszta és biztonságos villamosenergia-ellátás". Az eddigiekben változatlan formában idéztük Rubbia kijelentéseit, jóllehet - mint az alábbiakból kiderül - jóformán egyikkel sem értünk maradéktalanul egyet.
Carlo Rubbia fentiekben vázolt javaslatát célszerű azokkal a problémákkal szembesíteni, amelyek a villamos energiának a létező atomerőművekben való termelését terhelik, nevezetesen:
Az alábbiakban tett észrevételeinket ezek szerint a szempontok szerint csoportosítjuk. A későbbiek jobb megértése érdekéhen érdemes két kérdéskört külön áttekinteni: az ismert nukleáris technológiák együttműködését és a tóriumciklus néhány kérdését.
A nukleáris triád
A ma ismert nukleáris technológiák három csoportba sorolhatók: hasadási technológia (reaktorok és a kapcsolódó iparágak), fúziós technológia és nyaláb/gyorsító technológia. E nukleáris triód egyes tagjai között az eddigiekben kevés kapcsolatot láttunk: az egyes területeken dolgozó tudóscsoportoktól kezdve a hatósági felügyeletig a három terület egymástól meglehetősen elhatárolódott. Még közös tudományos konferenciákra is csak kivételesen lehet példát találni, hiszen alig van egymásnak szóló mondanivalójuk. Ennek ellenére az ötvenes évektől kezdve napirenden van e területek együttműködése - de csak tanulmányi szinten. Bár, mint látni fogjuk, eredetinek nem tekinthető, Rubbia javaslata éppen amiatt érdemel figyelmet, hogy a CERN egyik gyorsítójánál végre gyakorlati lépést szándékozik tenni, és így a hasadási és a gyorsítós technológia szinenergetikus alkalmazásának a problémáit kísérletileg is vizsgálni lehet.
A két technológia együttes alkalmazására először 1952-ben tett W.B. Lewis (Kanada) javaslatot. Ő éppen tóriumban javasolta hasadóanyag tenyésztését gyorsítóban kapott spallációs neutronok felhasználásával. A későbbiekben mások is (amerikaiak, szovjetek) vizsgáltak hasonló rendszereket. A tisztán hasadási technológia útján való tenyésztéssel szemben a spalláció/hasadás kombinációnak az a legfőbb előnye, hogy a spalláció neutronokban sokkal gazdagabb reakció, mint a hasadás: hasadásonként 2-3 neutront kapunk, egy spallációban pedig 20-40-et. Ha a kombinált rendszerben a reaktor szubkritikus, ez a neutronháztartás számára két előnnyel is jár: (1) A kritikus reaktorban az amúgy is kevés hasadási neutronból 1-et a láncreakció fenntartására kell fordítani és csak a fennmaradó neutronok egy része használható tenyésztésre. A szubkritikus rendszer ezzel szemben a spallációs neutronforrást még meg is sokszorozza. (2) Az atomerőműben a hasadóanyag fogyásának az ellensúlyozására a reaktor indításakor tartalékreaktivitást kell beépíteni, amelynek a kimerülésekor az erőművet átrakás céljából le kell álltani. Külső forrással meghajtott szubkritikus reaktor működése tartalékreaktivitást nem igényel, így neutronfizikai szempontból a kombinált rendszer tetszőleges ideig üzemben tartható, pontosabban az üzembentartósnak csak biztonsági és technológiai korlátai vannak. Ezekre még visszatérünk.
A három nukleáris technológia egyéb kombinációit is felvetették, amelyek közül számosan a jövőben bizonyára fontos szerepet fognak játszani. Például, a nukleáris triód eddig nem említett tagja, a fúzió is gazdag neutronokban. Ezért a fúzióval kapcsolatban is kezdettől fogva felmerült a hibrid hasadási/fúziós rendszer gondolata, amelyben a fúziós rendszerből kiszökő neutronokat szintén hasadóanyag-tenyésztésre használnák fel. Itt még indokolt a feltételes mód használata, hiszen a fúziós technológia ma még nem realitás - szemben a gyorsítóval. A kombináció másik irányban is hasznos lehet: a fúziós reakciót egy reaktorral táplált lézerrel gyújtják be. Témánktól messze vezetne további érdekes kombinációk sorolása.
A spalláció/hasadás kombinációhoz visszatérve megjegyezzük, hogy ennek jelenleg legkomolyabban vizsgált alkalmazását Rubbia is említi: a lassan bomló aktinidák transzmutációja gyorsabban bomló hasadási termékekké. Elképzelhető, hogy ez az eljárás az atomerőművi nagy aktivitású hulladékok kezelésének fontos eszköze lesz. Ennek azonban van egy "versenytársa" is: az aktinidáknak gyorsreaktorban való elégetése. Nehéz ma megmondani, hogy melyik eljárás kerül ki végülis győztesen, ha az aktinidák transzmutációjára egyáltalán sor kerül egyszer.
A tóriumciklus reaktorban
A természetben előforduló két fertilis izotóp (238U és 232Th) mindegyike egy-egy tenyésztési ciklus kiindulópontja. Az új hasadóanyag termelését a C konverziós tényezővel jellemezzük: a reaktorban egy adott idő alatt keletkező új hasadóanyag tömegének és az eredetileg bevitt hasadóanyagból eközben elhasznált rész tömegének a hányadosa. Tenyésztésről akkor szoktunk beszélni, amikor C > 1. Ebben az esetben a leállított reaktorban több hasadóanyag található, mint amennyit induláskor belevittünk. Ha ezt reprocesszálás útján a kirakott üzemanyagból rendeszeresen kivonjuk, és a későbbiekben reaktorba visszavisszük, akkor nyilvánvalóan a teljes fertilisanyag-készletet hasadóanyaggá tudjuk átalakítani. Abban az esetben, ha C< 1, csak konverzióról szoktunk beszélni. Ilyenkor a fertilisanyag-készletnek csak egy része alakítható át hasadóanyaggá. A termelhető új hasadóanyag mennyiségére egyszerűen kaphatunk egy felső korlátot. Jelöljük M-mel a természetben található hasadó izotóp össztömegét, és legyen M' az ennek elfogyása során felhasznált összes hasadóanyag tömege. Ekkor a konverziós tényező fenti definíciója alapján írhatjuk, hogy
(3)
M' = M+M' C,
amiből
![]()
A szokványos vizes reaktorokban C tipikus értéke 0,6, vagyis ezekkel a meglévő hasadóanyag mennyiségének legjobb esetben is csak a 2,5-szeresét tudjuk hasznosítani. Grafitos rendszerekben C![]() 0,8 amivel már 5-szörös hasznosítást érhetünk el, de nyilvánvaló, hogy az igazi megoldást a tenyésztő reaktorok adják.
0,8 amivel már 5-szörös hasznosítást érhetünk el, de nyilvánvaló, hogy az igazi megoldást a tenyésztő reaktorok adják.
A konverziós tényező szempontjából a kiindulási hasadó izotópnak a következő paramétere a mérvadó:
(4)
![]()
ahol v a hasadásban keletkező neutronok száma. Mivel 1 neutron szükséges a láncreakció fenntartásához, tenyésztés csak akkor lehetséges, ha ![]() > 2.
> 2. ![]() értéke függ a hasadást kiváltó neutron energiájától. Az alábbi táblázatban megadjuk a három legfontosabb hasadó izotóp
értéke függ a hasadást kiváltó neutron energiájától. Az alábbi táblázatban megadjuk a három legfontosabb hasadó izotóp ![]() -ját gyors (néhány 100 keV energiájú) és termikus energiájú neutronok által kiváltott hasadásokra vonatkozóan:
-ját gyors (néhány 100 keV energiájú) és termikus energiájú neutronok által kiváltott hasadásokra vonatkozóan:
|
izotóp |
|
|
|
233 U |
2,29 |
2,45 |
|
235 U |
2,07 |
2,3 |
|
239 Pu |
2,09 |
2,7 |
Tekintve, hogy reaktorban a szabályozás, kiszökés és parazita neutronbefogás is fogyaszt neutronokat, ![]() -nak jelentősen 2 felett kell lennie ahhoz, hogy C> 1 lehessen. A gyors neutronok által kiváltott hasadások esetében ez teljesül, így gyorsreaktorban a tenyésztés minden (reaktorfizikai) nehézség nélkül lehetséges. Termikus reaktorban azonban tenyésztésről legfeljebb az 233U esetében lehet szó. Könnyűvízzel moderált, 233U-os reaktorban C
-nak jelentősen 2 felett kell lennie ahhoz, hogy C> 1 lehessen. A gyors neutronok által kiváltott hasadások esetében ez teljesül, így gyorsreaktorban a tenyésztés minden (reaktorfizikai) nehézség nélkül lehetséges. Termikus reaktorban azonban tenyésztésről legfeljebb az 233U esetében lehet szó. Könnyűvízzel moderált, 233U-os reaktorban C![]() 0,8, viszont grafit és nehézvíz moderátor és 233U esetében C megközelíti az 1-et.
0,8, viszont grafit és nehézvíz moderátor és 233U esetében C megközelíti az 1-et.
Az elvégzett vizsgálatok alapján úgy tűnik hogy tóriumot és 233U-t a jelenleg működő reaktorok bármelyikében lehet alkalmazni. A kanadai CANDU reaktor moderátora nehézvíz, üzemanyaga természetes urán. Az üzemviteli tapasztalatok mind biztonsági, mind gazdaságossági szempontból kedvezőek. 1980 óta folynak vizsgálatok az ebbe a reaktorba helyezett 232Th alapú üzemanyagra vonatkozóan. A számítások szerint C értéke 1,01 és 1,02 között lehet, amit - 0,5 %-ot nem meghaladó reprocesszálási veszteség mellett - hasadóanyag-tenyésztést tesz lehetővé. Az alábbiakban többször visszatérünk még a német AVR reaktorhoz (Jülich), amelynek a moderátora grafit, üzemanyaga tóriummal kevert dúsított urán. Ez a rendszer témánk szempontjából azért érdekes, mert fűtőelemei ugyanazok a golyók, amelyeket Rubbia is javasol. Nem állítható, hogy ez a rendszer tenyésztést valósít meg, de ahhoz mindenképpen közel áll. Végső soron tehát igaz, hogy a tóriumciklus reaktorban reálisan is tenyésztővé (de legalábbis majdnem tenyésztővé) tehető. Mivel a moderátor lehet akár grafit, akár nehézvíz, gyakran párhuzamosan fogunk utalni az AVR-re és a CANDUra az egyes kérdések tárgyalásakor.
Nézzük most meg, milyen szempontok indokolnák a tóriumciklus gyakorlati alkalmazását. A legelső szempont mindenképpen az urán megtakarítása. Vannak országok, amelyekben lényegesen több tórium található, mint urán. Közülük először India említendő, ahol a nem kis uránkészleteket sokszorosan felülmúló tóriumkészlet van. Ezért India igen aktív ezen a területen: már épített kritikus rendszert, és előrehaladott állapotban van Kalpakkamban egy 30 kW teljesítményű, 233U/Al ötvözet üzemanyaggal működő reaktor létesítése. Jelentős aktivitást fejt ki ezen a területen még Japán, Franciaország, Kanada és Németország. Az utóbbiakban azonban az urán megtakarításának az igénye nem ennyire nyilvánvaló, sőt ma inkább ennek az ellenkezője igaz:
tekintve, hogy új atomerőművet az elmúlt években nem rendeltek, jelenleg mindenütt az uránár csökkenése tapasztalható. Emiatt a tóriumciklus nagyléptéke alkalmazása gazdaságilag ma nem indokolt. Általános vélemény, hogy az uránárnak a jelenlegi 2-3-szorosára kell nőnie ahhoz, hogy a tóriumciklus gazdaságilag érdekes legyen. Ebben az esetben indokolttá válik a reaktorból kirakott üzemanyag reprocesszálása is. Amíg pedig erre nincs gazdasági indíték, addig az ezzel kapcsolatos biztonsági kockázatokat a jelenlegi társadalmi közegben aligha fogják valahol is vállalni. Reprocesszálás nélkül pedig a tóriumciklusnak sincs értelme. Ez az állítás természetesen csak a reaktoros technológiára érvényes. Ha viszont a Rubbia által javasolt kombinált rendszer tényleg kiküszöböli a reprocesszálást, ez a tóriumciklust teljesen új megvilágításba helyezi.
Egyelőre még maradjunk a reaktoroknál, és tételezzük fel, hogy egyszer eljön az az idő, amikor a reprocesszálásra nagy léptékben sor kerül. Nézzük meg, hogy a tóriumciklusnak ebben az esetben milyen előnyei és hátrányai vannak az uránciklushoz képest:
- A tóriumciklusban (egyszerűen a kisebb kiinduló rendszám miatt) kereken 1000-szer kevesebb aktinida keletkezik, mint az U/Pu ciklusban. Ez jelentűsen egyszerűsíti a hulladékok elhelyezését (vesd össze Rubbia fenti b) szempontját).
- Tekintve, hogy a tóriumnak nincs haladóképes izotópja, a tóriumos reaktorba induláskor hasadóanyagot kell bevinni. Ez a fentiekben említett három hasadó izotóp bármelyike lehet. A lehetőségek közül kiemelendő a CANDU, amelybe az induló hasadóanyag-tölteten kívül további hasadóanyagot nem kell bevinni (reprocesszálás esetén). (Ebben a tekintetben a spalláció/hasadás kombináció ennél annyiban egyszerűbb, hogy még a kezdeti hasadóanyagra sincs feltétlenül szükség)
- Ma úgy tartják, hogy a tóriumkészletek az uránkészletek 3-szorosát teszik ki, továbbá a tórium egyenletesebben oszlik el a világon, mint az urán.
-A Th/U ciklusban keletkezik 232U, amelynek a bomlástermékei között található 208TI és 212Bi. Ezek 1,8 illetve 2,6 MeV-es ![]() -sugarakat emittálnak. Emiatt az 233U-tartalmú fűtőelemek gyártása drágább (távvezérelt) technológiát igényel, mint az U/Pu ciklus fűtőelemeié. Ha ezt a bonyodalmat meg akarjuk takarítani, akkor szóba jöhet e két izotópnak a reprocesszáláskor való kiküszöbölése. Emiatt nem igazán érv, amit Rubbia e) alatt a terroristákra vonatkozóan állít. Ha a kemény
-sugarakat emittálnak. Emiatt az 233U-tartalmú fűtőelemek gyártása drágább (távvezérelt) technológiát igényel, mint az U/Pu ciklus fűtőelemeié. Ha ezt a bonyodalmat meg akarjuk takarítani, akkor szóba jöhet e két izotópnak a reprocesszáláskor való kiküszöbölése. Emiatt nem igazán érv, amit Rubbia e) alatt a terroristákra vonatkozóan állít. Ha a kemény ![]() -sugárzást az 233U emittálná, talán igaza lenne, de véleményünk szerint nem erről van szó: az 233U által emittált legkeményebb
-sugárzást az 233U emittálná, talán igaza lenne, de véleményünk szerint nem erről van szó: az 233U által emittált legkeményebb ![]() -foton energiája 400 keV, ami nem lényegesen keményebb az 235U
-foton energiája 400 keV, ami nem lényegesen keményebb az 235U ![]() -fotonjainál (200 keV). Emiatt vitatjuk Rubbia idizett állítását.
-fotonjainál (200 keV). Emiatt vitatjuk Rubbia idizett állítását.
- A 233Pa viszonylag hosszú felezési ideje (27 nap) a reaktor leállása után reaktivitásgondokat okoz: a belőle keletkező hasadóanyag mennyisége 1,5 és 4 % közötti reaktivitás bevitelét jelenti, ami bonyolítja a tárolást. A probléma érzékeltetéséhez megjegyezzük, hogy a sokszorozási tényezőnek a hasonló tárolók számára általában előírt felső korlátja 0,95, vagyis a szokásos biztonsági tartalék 5 %.
- A fentieken túlmenően már csak egy hátrányt említünk meg: a Csernobilban olyan jelentős szerepet játszott üregegyüttható egy Th/U-os reaktorban lehet pozitív.
A reprocesszálás és a fűtőelemgyártás területén tovább lehetne folytatni az összehasonlítást. Így is látható azonban, hogy az összehasonlítás mind az U/Pu, mind a Th/U ciklus számára ad előnyöket és hátrányokat. Ilyen módon az az általános vélemény, hogy a tóriumciklus alkalmazását illetően a döntő az uránár alakulása lesz.
E rész befejezéséül még annyit jegyzünk meg, hogy a tóriumciklus ipari léptékű alkalmazása a következő izotópok nukleáris adatainak a jelenleginél jóval pontosabb ismeretét igényelné: 232Th (a gyors neutronokra vonatkozó hatáskeresztmetszetek), 233U (főleg a befogási hatáskeresztmetszet és a (4) alatt definiált ![]() ), 234U és 233Pa (minden hatáskeresztmetszet). Az utóbbi két izotóp esetében a jelenlegi adatok annyira hozzávetőlegesek, hogy még pontosságukra vonatkozóan sincsenek megbízható becslések.
), 234U és 233Pa (minden hatáskeresztmetszet). Az utóbbi két izotóp esetében a jelenlegi adatok annyira hozzávetőlegesek, hogy még pontosságukra vonatkozóan sincsenek megbízható becslések.
Az energiasokszorozó
Nézzük meg ezek után, milyen válaszokat ad a Rubbia által javasolt energiasokszorozó a bevezetésben említett problémákra. Az energiasokszorozóban keletkező hulladékok és melléktermékek előnyös vagy hátrányos tulajdonságairól az energiasokszorozó vonatkozásában ugyanazt lehet elmondani, mint amit a reaktoros tóriumciklusról már elmondtunk. Ezért a hulladékok kérdését külön nem tárgyaljuk.
A felhasználható hasadóanyag mennyisége
Előadásában Rubbia megadja az energiasokszorozóban keletkező új hasadóanyag (233U) mennyiségét. Tekintve, hogy egyenletei több ponton korrekcióra szorulnak, ezeket újra felírjuk. Könnyen belátható, hogy a 233Th rövid felezési ideje (23 perc) miatt úgy tekinthetjük, mintha a 232Th neutronbefogása után azonnal 233Pa keletkezne. Ezzel az elhanyagolással a tóriumciklus egyenletei így írhatók:
(5a)
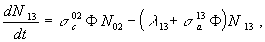
(5b)
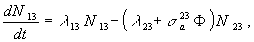
ahol a szokásos konvenció szerint az indexek jelentése: 02 a 232Th-ot, 13 a 233Pa-ot, 23 pedig az 233U-t jelöli.
Az (5b) egyenlet megfelelőjében Rubbia a 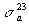 helyett
helyett
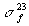 -et ír ami elírás, hiszen nemcsak a hasadás, hanem a neutronbefogás is csökkenti az 233U magok számát. (Abszorpció = hasadás + befogás.) Emiatt (2)-ben 0,0135 helyett 0,0128-nak kellene állnia. Az 233U lassan bomlik, ezért energiatermelő rendszerek esetében
(5b)-ben
-et ír ami elírás, hiszen nemcsak a hasadás, hanem a neutronbefogás is csökkenti az 233U magok számát. (Abszorpció = hasadás + befogás.) Emiatt (2)-ben 0,0135 helyett 0,0128-nak kellene állnia. Az 233U lassan bomlik, ezért energiatermelő rendszerek esetében
(5b)-ben ![]() <<
<<
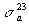
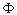 ,
tehát
,
tehát ![]() elhagyható.
(5a) megfelelőjében Rubbia nem szerepelteti a
elhagyható.
(5a) megfelelőjében Rubbia nem szerepelteti a 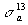 tagot, hiszen a
tagot, hiszen a 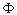 fluxust úgy kívánja megválasztani,
hogy
fluxust úgy kívánja megválasztani,
hogy 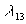 >>
>> 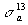
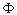 legyen (vesd össze a (4) egyenletet). Mi megtartjuk, mert ez szükséges a 233Pa szerepének a tisztázásához. Egyenleteinkben N02, N13 és N23 szigorúan véve az indexszel jelölt atommagok számát jelentik, de - a 232 és 233 tömegszámok közötti kis különbséget elhanyagolva - úgy is tekinthetjük ezeket a mennyiségeket, mint a megfelelő izotópoknak a reaktorban levő össztömegét.
legyen (vesd össze a (4) egyenletet). Mi megtartjuk, mert ez szükséges a 233Pa szerepének a tisztázásához. Egyenleteinkben N02, N13 és N23 szigorúan véve az indexszel jelölt atommagok számát jelentik, de - a 232 és 233 tömegszámok közötti kis különbséget elhanyagolva - úgy is tekinthetjük ezeket a mennyiségeket, mint a megfelelő izotópoknak a reaktorban levő össztömegét.
Az (5) egyenletrendszer megoldása nagy t időkre:
(6)
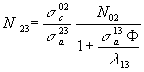
Kisebb t-re (6)-ban két exponenciális tag veendő figyelembe, amelyek közül a lassabban változó exp
(-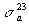
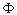 t)-vel arányos.
Mivel
t)-vel arányos.
Mivel 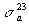 = 578 barn, ez
= 578 barn, ez 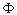 t
t
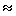 1022
n/cm2 integrált fluxus elérésekor válik elhanyagolhatóvá.
1022
n/cm2 integrált fluxus elérésekor válik elhanyagolhatóvá.
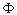 = 1014 a/cm2s fluxus esetében ez (kereken) 3 év alatt következik be. Jóllehet a teljesítmény pillanatnyi értékében ezek az eponenciális tagok ilyen t-re már elhanyagolhatók, az energiasokszorozó bekapcsolásától eltelt t idő alatt termelt összenergia számításában azonban ezeket a tagokat is figyelembe kell venni:
= 1014 a/cm2s fluxus esetében ez (kereken) 3 év alatt következik be. Jóllehet a teljesítmény pillanatnyi értékében ezek az eponenciális tagok ilyen t-re már elhanyagolhatók, az energiasokszorozó bekapcsolásától eltelt t idő alatt termelt összenergia számításában azonban ezeket a tagokat is figyelembe kell venni:
(7)
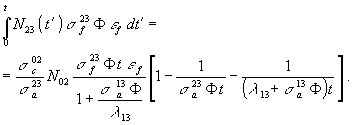
ahol ![]() az egy hasadásban keletkező energia
(
az egy hasadásban keletkező energia
(![]() 200 MeV). Az []-ben az 1 mellett szereplő tagok 10 %ot is meghaladó korrekciót jelentenek.
200 MeV). Az []-ben az 1 mellett szereplő tagok 10 %ot is meghaladó korrekciót jelentenek.
Az energiasokszorozóval termelhető energia szempontjából a döntő kérdés az, hogy mekkora lehet
a 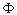 t integrált fluxus, hiszen (7) szerint a termelt összenergia ezzel monoton nő. A reaktor egy töltetéből kinyerhető energiát általában 1 tonna bevitt üzemanyagra vonatkozóan szokás megadni, rendszerint MW nap/tonna egységekben. Ezt a fajlagosan termelhető energiát kiégésnek szoktuk nevezni. Az "üzemanyagba" általában beleértenek minden nehézfémet, tehát dúsított urán esetében a két uránizotóp, tórium/urán esetében pedig a két fém együttes tömegét. Reaktorban a kiégést két dolog korlátozza: van egy reaktorfizikai korlát (a bevitt reaktivitástartalék nagysága), de van egy technológiai/biztonsági korlát is (a fűtőelemek roncsolódása az energiatermelés során keletkező hasadási termékek felhalmozódása miatt). A szokványos nyomottvizes atomerőművekben a reaktorfizikai korlát 30 ezer MWnap/tonna átlagos kiégést tesz lehetővé, ha az egyes fűtőelemkötegek 3-3 évet töltenek a reaktorban. Ugyanakkor a technológiai korlát ennek legalább a kétszeresét is megengedné: a vizsgálatok kimutatták, hogy a jelenlegi fűtőelemek 60 ezer MW nap/tonna kiégés esetén sem lyukadnak ki, és így biztonsággal nem kerülnek ki belőlük hasadási termékek. Rubbia energiasokszorozójában a reaktorfizikai korlát elesik, így itt a technológiai korlátot kell alapul vennünk. Mielőtt az általa javasolt fűtőelemek számszerű jellemzőire térnénk, általában megjegyezzük, hogy tévedés azt állítani, hogy az energiasokszorozó tetszőleges ideig üzemben tartható: azokat a fűtőelemeket, amelyek kiégése elérte a technológiai korlátot, friss fűtőelemekre kell cserélni. Jelöljük b-vel a kiégésnek a választott fűtőelemtípusra vonatkozó korlátját MWnap/g (vagyis millió MWnap/tonna) egységekben kifejezve, és (7) alapján becsüljük meg, mekkora
t integrált fluxus, hiszen (7) szerint a termelt összenergia ezzel monoton nő. A reaktor egy töltetéből kinyerhető energiát általában 1 tonna bevitt üzemanyagra vonatkozóan szokás megadni, rendszerint MW nap/tonna egységekben. Ezt a fajlagosan termelhető energiát kiégésnek szoktuk nevezni. Az "üzemanyagba" általában beleértenek minden nehézfémet, tehát dúsított urán esetében a két uránizotóp, tórium/urán esetében pedig a két fém együttes tömegét. Reaktorban a kiégést két dolog korlátozza: van egy reaktorfizikai korlát (a bevitt reaktivitástartalék nagysága), de van egy technológiai/biztonsági korlát is (a fűtőelemek roncsolódása az energiatermelés során keletkező hasadási termékek felhalmozódása miatt). A szokványos nyomottvizes atomerőművekben a reaktorfizikai korlát 30 ezer MWnap/tonna átlagos kiégést tesz lehetővé, ha az egyes fűtőelemkötegek 3-3 évet töltenek a reaktorban. Ugyanakkor a technológiai korlát ennek legalább a kétszeresét is megengedné: a vizsgálatok kimutatták, hogy a jelenlegi fűtőelemek 60 ezer MW nap/tonna kiégés esetén sem lyukadnak ki, és így biztonsággal nem kerülnek ki belőlük hasadási termékek. Rubbia energiasokszorozójában a reaktorfizikai korlát elesik, így itt a technológiai korlátot kell alapul vennünk. Mielőtt az általa javasolt fűtőelemek számszerű jellemzőire térnénk, általában megjegyezzük, hogy tévedés azt állítani, hogy az energiasokszorozó tetszőleges ideig üzemben tartható: azokat a fűtőelemeket, amelyek kiégése elérte a technológiai korlátot, friss fűtőelemekre kell cserélni. Jelöljük b-vel a kiégésnek a választott fűtőelemtípusra vonatkozó korlátját MWnap/g (vagyis millió MWnap/tonna) egységekben kifejezve, és (7) alapján becsüljük meg, mekkora
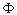 t integrált fluxusnak felel ez meg.
t integrált fluxusnak felel ez meg.
Becslésünkben a következő egyszerű ökölszabályból indulunk ki: 1 g hasadóanyag hasadása révén 1 MW nap energiát nyerünk. (Néhány % pontossággal ez minden hasadó izotópra igaz) Ha (7)-ben N02 az energiasokszorozóban levő tórium grammban kifejezett össztömegét jelenti, akkor ökölszabályunk alapján a következő feltételt kapjuk:
(8)
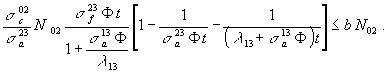
Itt N02-vel nyílván lehet egyszerűsíteni, de ezt a későbbiek kedvéért nem tesszük meg. (Egyszerűsítés után a jobboldal dimenziója MW nap/g, a baloldal pedig csak látszólag válik dimenzió nélkülivé, hiszen ökölszabályunk szerint benne van egy közelítőleg 1 értékű, szintén MWnap/g dimenziójú szorzó.) Számoljunk a Rubbia előadásában használt
hatáskeresztmetszetekkel: 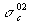 /
/
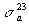 = 0,0128;
= 0,0128;
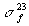 = 523 barn;
= 523 barn;
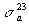 = 578 barn;
= 578 barn;
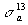
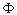 /
/
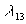 = 0,02.
= 0,02.
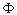 = 1,5
= 1,5
 1014 n/cm2s mellett ezekkel a számadatokkal a
1014 n/cm2s mellett ezekkel a számadatokkal a
(9)
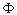 t
t
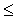 1,5
1,5  b
b  1023 n/cm2
1023 n/cm2
felső korlát adódik. (Vigyázzunk, itt újra nem írtuk ki az 1 MW nap/g értékű tényezőt!) A megadott számértékek alapján reflektálhatunk Rubbia d) állítására is, miszerint az energiasokszorozó az összetétel-változásokkal szemben stabil. Az állítás igaz, hiszen a rendszer összetétele valóban spontán visszaáll a (6) által megadott értékre. Ennek azonban két jellegzetes időállandója van: az egyik a 233Pa felezési ideje, vagyis 27 nap, a másik a már több képletben
megjelent 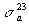
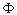 szorzat, amelynek a reciproka 133 nap. Ez azt jelenti, hogy a magára hagyott energiasokszorozóban az összetétel 4-5 hónapos időskálán áll vissza állandósult értékére. Egy villamosenergia-rendszerbe kapcsolt berendezést ilyen időskálán sohasem hagynak magára, hiszen a belőle kivett energia napos, sőt órás időskálán változik az energiarendszer igényei szerint. Ezért, jóllehet Rubbia d) állítása elvileg igaz, a gyakorlati alkalmazás szempontjából érdektelen.
szorzat, amelynek a reciproka 133 nap. Ez azt jelenti, hogy a magára hagyott energiasokszorozóban az összetétel 4-5 hónapos időskálán áll vissza állandósult értékére. Egy villamosenergia-rendszerbe kapcsolt berendezést ilyen időskálán sohasem hagynak magára, hiszen a belőle kivett energia napos, sőt órás időskálán változik az energiarendszer igényei szerint. Ezért, jóllehet Rubbia d) állítása elvileg igaz, a gyakorlati alkalmazás szempontjából érdektelen.
A Rubbia által javasolt golyó alakú fűtőelem a gyakorlatban ismert: ez a fűtőeleme a magas hőmérsékletű (HTR) reaktoroknak. Ilyen például a Jülichben (Németország) épült AVR. Itt az urán (és a tórium) kis burkolt szemcsék formájában grafit golyókba van ágyazva. (Egy szemcsén belül az urán nem keveredik a tóriummal.) A szemcsék átmérője 0,4 mm, a golyóké 6 cm. Egy golyóban (kerekítve) 10 g táriumoxid és 1 g uránoxid van. Az urán dúsítása 93 %. A reaktor hűtőközege a golyók között áramló hélium gáz. Emiatt a vízzel hűtött reaktorokhoz képest itt lényegesen magasabb kilépő hőmérsékletek (950 °C) érhetők el. Ez a magyarázata a "magashőmérsékletű reaktor" elnevezésnek. Az említett reaktor fontosabb adatai:
Rubbiánál 1 tonna tóriumra 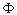 =
1,5
=
1,5 1014 n/cm2s neutronfluxus mellett 50 MW hőteljesítmény adódik. A két rendszer tehát egymáshoz meglehetősen hasonló. Az AVR-ben a kiégés reaktorfizikai korlátja 130 ezer MW nap/tonna, a technológiai korlát pedig 190 ezer MW nap/tonna, vagyis b = 0,19 MW nap/g. Ezzel (9) alapján a
1014 n/cm2s neutronfluxus mellett 50 MW hőteljesítmény adódik. A két rendszer tehát egymáshoz meglehetősen hasonló. Az AVR-ben a kiégés reaktorfizikai korlátja 130 ezer MW nap/tonna, a technológiai korlát pedig 190 ezer MW nap/tonna, vagyis b = 0,19 MW nap/g. Ezzel (9) alapján a
(9a)
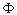 t
t 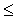 2,9
2,9  1022
n/cm2
1022
n/cm2
felső korlát adódik az integrált fluxusra. A fenti
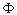 neutronfluxussal számolva ez azt jelenti, hogy az energiasokszorozó fűtőelemei 5,9 évig maradhatnak a reaktorban. Ez kereken kétszerese a szokványos nyomottvizes atomerőművekre jellemző értéknek. Ennek elteltekor a (6) képlet szerint számolható mennyiségű hasadóanyag található a rendszerben.
neutronfluxussal számolva ez azt jelenti, hogy az energiasokszorozó fűtőelemei 5,9 évig maradhatnak a reaktorban. Ez kereken kétszerese a szokványos nyomottvizes atomerőművekre jellemző értéknek. Ennek elteltekor a (6) képlet szerint számolható mennyiségű hasadóanyag található a rendszerben.
Mielőtt tovább mennénk, közbevetőleg megjegyezzük, hogy dúsított urán és grafit moderátor esetében szokatlanul kicsinek tűnik az 1,017 értékű k![]() (= a minden irányban végtelen méretű reaktor sokszorozási tényezője). Ezt azért választották ilyen kicsinek, mert így lehet nagy a kritikus tömeg, és így lehet a reaktorban a fent megadott neutronfluxus mellett a szükséges hőteljesítményt elérni. Ha a grafit/urán arányt csökkentjük, k
(= a minden irányban végtelen méretű reaktor sokszorozási tényezője). Ezt azért választották ilyen kicsinek, mert így lehet nagy a kritikus tömeg, és így lehet a reaktorban a fent megadott neutronfluxus mellett a szükséges hőteljesítményt elérni. Ha a grafit/urán arányt csökkentjük, k![]() értéke lényegesen nagyobb is lehet. Egyébként HTR típusíj reaktorok nemcsak Németországban, hanem az USÁ-ban is vannak. Adataik csak a reaktor méretében különböznek az AVR-től lényegesen, ezért elég az AVR-rel foglalkozni.
értéke lényegesen nagyobb is lehet. Egyébként HTR típusíj reaktorok nemcsak Németországban, hanem az USÁ-ban is vannak. Adataik csak a reaktor méretében különböznek az AVR-től lényegesen, ezért elég az AVR-rel foglalkozni.
Az energiasokszorozó megítélése szempontjából érdekes megbecsülni, hogy ez alatt a 6 év alatt az energiasokszorozó a tórium hány százalékát alakította át hasadóvá. Ha a reaktorból kirakott elhasznált fűtőelemeket nem reprocesszálják, akkor a következőképpen okoskodhatunk. A (8) képlet szerint bN02 = 0,19 N02 MW nap energiát nyerhetünk N02 gramm tóriumból, ami ökölszabályunk szerint ugyanennyi gramm hasadóanyag felhasználásával egyenértékű. Azt látjuk tehát, hogy az eredetileg bevitt tórium 0,19-szeresét, tehát 19 %-át hasznosíthatjuk ilyen módon. Az a körülmény, hogy ezt reprocesszálás nélkül sikerül megtenni, véleményünk szerint az energiasokszorozó legnagyobb érdeme. Az eddig megvalósított nukleáris technológiák egyike sem képes erre. Megjegyezzük, hogy más típusú fűtőelemek esetében a b felső határ alacsonyabb (100 ezer MW nap/tonna vagy kevesebb), tehát ezekkel a tóriumnak 10 % körüli (vagy kisebb) hányadát lehet hasadóvá tenni és energiatermelésre hasznosítani. Látjuk tehát, hogy az energiasokszorozó megítélése szempontjából a választott fűtőelem típusa erősen nyom a latba. (Megfontolásainkban elhanyagoltuk a reaktoron belüli teljesítményeloszlást. Emiatt 19 %-nál kisebb szám a reális érték.
Reprocesszálás esetén nyilvánvaló, hogy a tórium teljes mennyisége hasadóvá tehető. A tóriumciklusról a fentiekben mondottak szerint azonban ebben az esetben a tisztán reaktoros technológiák is képesek ugyanerre, tehát az energiasokszorozónak az imént talált előnye reprocesszálás esetén már nem ennyire nyilvánvaló: jóllehet a gyorsítós tenyésztés hatékonyabb (nagyobb C rendelhető hozzá), mint a reaktoros, ma nem a tenyésztés hatékonysága a vitatott probléma, hanem az, hogy egyáltalán legyen-e reprocesszálás.
A kiégés technológiai korlátjának a fenti módon való figyelembe vétele nem triviális, ezért ezt közelebbről meg kell még világítanunk. A (6) összefüggés szerint - a fenti számértékekkel számolva - az energiasokszorozóan a hasadóanyag állandósuló mennyisége a tóriumnak 1,3 %-a. Ha ezt dúsításnak tekintjük, akkor összevethetjük a kis dúsítású reaktorokkal. Önként adódó példa a nehézvízzel moderált és hűtött CANDU, amelynek az üzemanyaga természetes urán. Az ebben reaktorfizikailag elérhető kiégés 8500 MW nap/tonna, bár maga a fűtőelem 50 ezer MW nap/tonna kiégést is megengedne. Ennek az elérése úgy válik az energiasokszorozóban lehetővé, hogy a külső neutronforrás (vagyis a gyorsító) az energia termelését mindaddig fenntartja, amíg az biztonságosan lehetséges. A fűtőelemek a hasadási termékeket megtartó tulajdonságukat attól függetlenül őrzik meg vagy veszítik el, hogy milyen módon idézzük elő a hasadásokat: láncreakció vagy külső neutronforrás révén. Ezért volt szabad megfontolásainkban a technológiailag lehetséges felső korlátot alapul venni.
E rész befejezéséül szenteljünk néhány megjegyzést Rubbia modelljének is:
- Feltűnő, hogy a 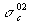 /
/ 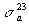 arányt (amely nála tévesen
arányt (amely nála tévesen
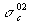 /
/ 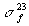 ) természeti állandónak minősíti. Az (5) egyenletrendszerben szereplő hatáskeresztmetszetek a neutronenergiától erősen függő hatáskeresztmetszeteknek a neutronspektrumra vett átlagai. A neutronspektrum az összetétel változásával erősen változik, emiatt nyilván változnak az átlagok is. Idézett kijelentése arra utal, hogy Rubbia modellje elhanyagolja a neutronspektrum változását. Ez annyira durva közelítés, hogy a modell csak kvalitatív következtetéseket tesz lehetővé.
) természeti állandónak minősíti. Az (5) egyenletrendszerben szereplő hatáskeresztmetszetek a neutronenergiától erősen függő hatáskeresztmetszeteknek a neutronspektrumra vett átlagai. A neutronspektrum az összetétel változásával erősen változik, emiatt nyilván változnak az átlagok is. Idézett kijelentése arra utal, hogy Rubbia modellje elhanyagolja a neutronspektrum változását. Ez annyira durva közelítés, hogy a modell csak kvalitatív következtetéseket tesz lehetővé.
- A modell elhanyagol nagyon fontos reakciókat, mint például a rezonanciabefogás, a tórium gyorshasadása stb. Ezek együttes hatása az érintett izotópok mennyiségében sokat jelenthet. Becsléseink szerint a tórium rezonanciabefogásai hozzávetőleg annyi uránt termelnek, mint a termikus energiákon bekövetkező reakciók. Ezért (2) jobboldalán körülbelül 0,025-nek kellene állnia (0,013 helyett).
- Ha - mint láttuk - a tórium mennyisége 19 %-kal csökken, már nem hanyagolható el az N02-nek a t-től való függése. A (6) egyenlet tehát már emiatt is közelítő.
- A 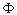 neutronfluxus nagyságát biztonsági megfontolások korlátozzák (lásd alább), és nem a 233Pa neutronbefogása, ami - Rubbia szerint - csökkenti a termelt energia mennyiségét. A (8) egyenlet mutatja, hogy ez a magreakció (a baloldalon a nevezőben levő tag révén) valóban csökkenti a reaktor pillanatnyi teljesítményét, de sem a termelt összenergia, sem pedig a hasadóvá tett tórium mennyisége nem csökken. Emiatt a Rubbia által (2) alatt definiált
neutronfluxus nagyságát biztonsági megfontolások korlátozzák (lásd alább), és nem a 233Pa neutronbefogása, ami - Rubbia szerint - csökkenti a termelt energia mennyiségét. A (8) egyenlet mutatja, hogy ez a magreakció (a baloldalon a nevezőben levő tag révén) valóban csökkenti a reaktor pillanatnyi teljesítményét, de sem a termelt összenergia, sem pedig a hasadóvá tett tórium mennyisége nem csökken. Emiatt a Rubbia által (2) alatt definiált ![]() semmiféle hatásfokként nem értelmezhető. Más kérdés persze, hogy a 233Pa neutronbefogása révén 234U keletkezik, amely kellemetlen (
semmiféle hatásfokként nem értelmezhető. Más kérdés persze, hogy a 233Pa neutronbefogása révén 234U keletkezik, amely kellemetlen (![]() -sugárzó) melléktermék. Ennek a többsége azonban az 233U neutronbefogása útján termelőik (legalábbis a választott neutronfluxus mellett).
-sugárzó) melléktermék. Ennek a többsége azonban az 233U neutronbefogása útján termelőik (legalábbis a választott neutronfluxus mellett).
Az alkalmazott modell felsorolt hiányosságai miatt arra a konklúzióra jutunk, hogy Rubbia javaslata egyelőre inkább tekinthető ötletnek, mint kiérlelt koncepciónak. A fentiekben talált előnyeire való tekintettel azonban érdemes az energiasokszorozót egy komolyabb reaktorfizikai analízisnek alávetni. Mint a tóriumciklusnál már említettük, a komolyabb analízis már atommagadat-problémákat is fel fog vetni, hiszen ezek ma a jobban ismert tóriumos reaktorok analízisét is nehezítik. Erre az alaposabb vizsgálatra a biztonsági kérdések elemzése miatt is szükség van.
Biztonság és gazdaságosság
Talán meglepő, hogy a fenti címben felvetjük a gazdaságosság kérdését egy ennyire csak ötletszerűen elképzelt berendezés esetében. Valóban komolytalan lenne, ha megkísérelnénk az energiasokszorozóban termelt villamos energia árát Forint/kWh-ban kiszámolni. A gazdaságosság felvetésével mindössze annyit kívánunk hangsúlyozni, hogy a nukleáris berendezésekben a felmerülő költségek túlnyomó része a biztonsági követelmények kielégítésére vezethető vissza. Az alábbiakban röviden azt tekintjük át, hogy a szokványos atomerőműveknek milyen költséges berendezéseit lehet az energiasokszorozóban elhagyni a biztonság sérelme nélkül. Annyi ugyanis mindenképpen kézenfekvő, hogy a kombinált berendezésnek jelentős előnyöket kell mutatnia a benne levő reaktor egymagában való alkalmazásához képest, különben nem térülne meg a gyorsítóra fordított költség.
Mivel itt új típusú nukleáris létesítményről van szó, engedélyezésében és társadalmi elfogadásában csak akkor reménykedhetünk, ha úgynevezett inherens biztonságú berendezésnek lehet minősíteni. Jelenlegi ismereteink szerint 4 elképzelés van ilyenek létrehozására:
- a már említett HTR magashőmérsékletű reaktor és a CANDU,
- a jelenlegi nyomottvizes atomerőművek javított konstrukciója és
- a svédek által javasolt PIUS reaktor.
A felsoroltak közül az első kettő létezik, a harmadik a rajzasztalokon van, végül a PILIS egy ígéretes elképzelés. Messze vezetne annak a tárgyalása, hogy ezek miért tekinthetők inherens biztonságúnak, ezért csak nagy vonalakban vázoljuk. Tudvalevő, hogy az atomerőműben a láncreakció leállítása után is folytatódik az energiatermelés: a felhalmozott hasadási termékek radioaktív bomlása a leállás utáni percekben az eredeti teljesítmény 7 %-át termeli. (Ezt nevezzük remanens hőnek.) Így a leállított reaktor hűtéséről is gondoskodni kell, és ezért számít a hűtőközeg elvesztése a legsúlyosabb balesetnek. A szokásos nyomottvizes reaktorokban emiatt a biztonsági hűtőberendezések bonyolult rendszere található, amelyek ilyenkor is gondoskodnak a reaktor hűtéséről. Ezekben a reaktorokban tehát a biztonság az üzemzavari hűtőrendszer időben való bekapcsolásától függ. Az új felfogás szerint arra célszerű törekedni, hogy a biztonság a reaktor szerkezetébe legyen beleépítve, vagyis a biztonságos működést ne egyes berendezések jó működése, hanem a fizika jól ismert törvényei garantálják. Ez utóbbi kritériumnak eleget tevő rendszereket minősítjük inherens biztonságúaknak.
A HTR teljesítménysűrűsége nagyon alacsony: 6 kW/liter. (Egy szokásos nyomottvizes reaktorban ugyanez megközelíti, sőt meg is haladhatja a 100 kW/litert). Emiatt a remanens hő olyan kis mértékű, hogy a leállított reaktor alig igényel hűtést. Megállapították, hogy ha a teljesítménysűrűséget még ennek is felére csökkentenék, akkor a hűtőközeg teljes elvesztése esetén sem melegednének fel a fűtőelemek annyira, hogy belőlük hasadási termékek lépjenek ki. Megjegyezzük, hogy a fent figyelembe vett ~ fluxus értéke ennek a teljesítménysűrűségnek felel meg. Ebből következik, hogy a fluxus értékét elsősorban ez a megfontolás korlátozza és nem az előző részben tárgyalt reaktorfizikai szempontok (vagyis a 233Pa neutronbefogása). Örvendetes, hogy Rubbia energiasokszorozója éppen ilyen típusú fűtőelemeken alapul, tehát ez - ismételjük kellően alacsony neutronfluxus esetén a hűtőközeg elvesztéssel szemben kielégítően biztonságosnak tekinthető. A HTR fűtőelemeken alapuló energiasokszorozóban ugyanúgy egyszerűsíthető az üzemzavari hűtőrendszer, mint magában a HTR-ben. A CANDU-nak ugyan egyéb okokból, de szintén megvan ez a kedvező tulajdonsága, tehát egy erre alapozott tóriumos rendszer is megfelelően biztonságos lehet. (A CANDU-ban elsősorban a benne levő nehézvíz nagy tömege miatt javul a biztonság.) A CANDU alkalmazásának további elemzését azonban elhagyjuk.
A biztonság másik kritériuma a kritikussági baleset kivédése. Ha igaz, hogy az energiasokszorozó teljes 6 éves üzeme alatt végig szubkritikus marad, akkor ez - első látásra - minden reaktorral szemben nemcsak biztonsági előny, hanem megtakarítás is, hiszen nincs szükség sem a szabályozó rudakra, sem a vízben oldott bórsavra, de az ezekkel együttjáró szabályozórendszerre és segédüzemekre sem, továbbá egyszerűsíthető a reaktor működését ellenőrző mérőrendszer. A fentiek szerint a tórium mennyiségének mintegy 2,5 %-a urán. Az AVR reaktorban ez az arány 10 %, és a reaktor így éppen hogy kritikus. (Fentebb láttuk, hogy a szándékosan kicsire választott k![]() miatt van ez így.) Ezért az energiasokszorozó kisebb uránhányada miatt valóban szubkritikus. Ha azonban figyelembe vesszük, hogy ez a nagy tömegben levő grafit neutronabszorpciójának a következménye, a dolog már nem ilyen egyszerű: a grafit mennyiségét csökkentve egyrészt nő az urán részaránya, másrészt csökken a grafit neutronabszorpciója. Végső soron a rendszer közeledik a kritikus állapothoz. Elképzelhető, hogy van olyan tórium/grafit arány, amely mellett a rendszer kritikussá is válik. Ennek ellenére az a véleményünk, hogy a kritikusság gondos tervezéssel elkerülhető - ha szükséges. (Látni fogjuk, a kritikus állapotot nem feltétlenül kell elkerülni.) Más a helyzet nehézvíz esetében, amelynek az abszorpciója a grafiténak a negyede, tehát ebben az esetben a reaktor valószínűleg kritikussá fog válni. Ezért a grafitos energiasokszorozó másképp viselkedik, mint a nehézvizes.
miatt van ez így.) Ezért az energiasokszorozó kisebb uránhányada miatt valóban szubkritikus. Ha azonban figyelembe vesszük, hogy ez a nagy tömegben levő grafit neutronabszorpciójának a következménye, a dolog már nem ilyen egyszerű: a grafit mennyiségét csökkentve egyrészt nő az urán részaránya, másrészt csökken a grafit neutronabszorpciója. Végső soron a rendszer közeledik a kritikus állapothoz. Elképzelhető, hogy van olyan tórium/grafit arány, amely mellett a rendszer kritikussá is válik. Ennek ellenére az a véleményünk, hogy a kritikusság gondos tervezéssel elkerülhető - ha szükséges. (Látni fogjuk, a kritikus állapotot nem feltétlenül kell elkerülni.) Más a helyzet nehézvíz esetében, amelynek az abszorpciója a grafiténak a negyede, tehát ebben az esetben a reaktor valószínűleg kritikussá fog válni. Ezért a grafitos energiasokszorozó másképp viselkedik, mint a nehézvizes.
A reaktor szubkritikus voltának néhány előnyét már említettük. Néhány további dologra is fel kell azonban hívni a figyelmet:
- Részletes és kísérletileg ellenőrzött számításokkal igazolandó, hogy a választott tórium/grafit arány mellett a rendszer minden körülmények között szubkritikus marad. Mint mondtuk, ekkor megtakaríthatók a szabályozórudak és a működtetésükkel együtt járó berendezések. Ez a beruházási költségek néhány százalékát jelenti. Ezen túlmenően valószínűleg egyszerűsödik a reaktor üzemeltetése is, bár ma nehéz felmérni, hogy a gyorsító és a reaktor együttes szabályozása milyen többlet bonyodalmakkal jár.
- A szubkritikus reaktor sokszorozási tényezője (keff) befolyásolja a kombinált berendezés gyorsítóolcíatát is. Tudjuk, hogy a reaktor 1 /(1-keff)-szeresére sokszorozza meg a forrásból jövő neutronok számát. A HTR fűtőelemekben nagyon sok grafit van, és emiatt az energiasokszorozó reaktorában keff értéke 0,5 körül van, vagyis a neutronsokszorozás alig 2-szeres. Becsüljük meg, mekkora neutronforrásra van ekkor szükség. A már említett 250 MW hőteljesítmény másodpercenként 7,8 1018 hasadást jelent. Ha nincs neutronsokszorozás, akkor ez ugyanennyi forrásneutront feltételez. Ha spallációnként 20 neutronnal számolunk, akkor ez 60 mA targetáramot igényel, ami 1 GeV protonenergia esetén a targeten 60 MW hőteljesítmény kiválását, továbbá naponta 12 g ólom fogyását eredményezi. Nem állítjuk, hogy nem lehetséges ekkora teljesítményt kihűteni, továbbá a targeten fogyó ólmot folyamatosan pótolni, de nincs bizonyítva, hogy ez olcsóbban oldható meg, mint a megtakarított szabályozó rendszer ára. Maga Rubbia 5 mA targetáramról beszél, ami azt jelenti, hogy 10-szeres neutronsokszorozást, vagyis keff = 0,9-et vesz alapul. Ha keff-et tovább közelítjük az 1-hez, a gyorsító targetárama tovább csökkenthető: például, keff= 0,99 esetén már 100-szoros a neutronsokszorozás. Ezzel viszont a reaktoroldalon járnak bonyodalmak:
A gyorsító rendelkezésre állása valószínűleg függvénye a targetáramnak. Emiatt a keff megválasztása kényes optimalizációs feladat: egyrészt a lehetőség szerint csökkenteni célszerű a targetáramot, másrészt minél távolabb kell maradni a kritikusságtól (hogy ne legyen szükség szabályozó rudakra). Ennek a megvalósíthatóságot illetően ma aligha lehetnek meg a kiindulási adatok.
- Egyelőre nincsenek biztonsági normák egy ilyen szubkritikus rendszerre vonatkozóan. Például, nincs szabályozva, mekkora számolt sokszorozási tényező mellett engedhető meg a szabályozó rudak nélküli üzem. Ez azért említendő külön, mert a keff megválasztásának imént tárgyalt problémájára ez is hatással van.
- Ha a reaktor induláskor csak tóriumot tartalmaz, akkor az első hónapokban csak a tórium gyorshasadásai termelik az energiát, ami az állandósuló teljesítménynek legfeljebb 8-10 %-a. Emiatt kezdetben az állandósuló fluxus 10-szeresére is szükség lehet, ami biztonsági szemponthól nem kívánatos. Jobb megoldásnak tűnik induláskor 2-3 % 235U-t keverni a tóriumhoz (ami az első hónapokban kiég, de áthidalja a kezdeti uránhiányos időszakot).
A víznek, mint hűtőközegnek az alkalmazása több szempontból is alaposan meggoncíolandó. Két problémát látunk. Egyrészt egy grafittal moderált és vízzel hűtött reaktorban pozitív az üregegyüttható. Fentebb említettük, hogy a tóriumos rendszerek még a víz/grafit kombináció nélkül is hajlamosak erre. Csernobil megmutatta, hogy ez milyen bajt tud okozni. Határozottan szubkritikus rendszerben ennek a jelentősége nyilvánvalóan kisebb, mint kritikusban. Láttuk azonban, hogy elképzelhető egy olyan optimum, amelynél a reaktor kritikushoz közeli állapotban van. Egy ilyen kellemetlen effektusnak a megléte emiatt aligha engedhető meg. Másrészt víz esetében szükség van egy nagy nyomásra méretezett tartályra. Az energiasokszorozóban elképzelt neutronfluxus kereken tízszerese a nyomottvizes reaktorokban szokásosnak. Emiatt itt a tartály sugárkárosodása is körülbelül ilyen mértékben megnő. Ez azt jelenti; hogy - a jelenlegi acélokkal - a tartály élettartama aligha lehet több, mint 5 év, hiszen a nyomottvizesekben ez 30-40 év. Természetesen több módon is lehet a sugárkárosodást csökkenteni, de ez olyan bonyodalom, amely a szokványos reaktorokban nincs meg. Emiatt csak a héliummal való hűtést tudjuk elképzelni.
Következtetések
Fenti rövid elemzésünk alapján a következő megállapítások tehetők:
Végső következtetésünk tehát az, hogy egy szempontot (lásd 2.) találtunk, amely szerint a kombinált rendszer egyértelműen előnyösebb, mint a gyorsító nélkül alkalmazott reaktor. A 4. szempont szerinti előny nem zárható ki, de ez még vizsgálandó. A többi szempont szerint talált előnyök a választott reaktortípusból erednek, tehát a kombináció ezek szerint különösebb előnyt nem nyújt. Mindenképpen azonban az energiasokszorozó alapos vizsgálatra érdemes, bár nem eredeti megoldás. Ezért egy részletes és pontos számításokon alapuló analízist látunk ajánlatosnak - első lépésben reaktorfizikai szempontból.