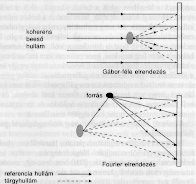
1. ábra. Hologramot sokféle geometriai elrendezésben készíthetünk. Itt a két leggyakrabban használt megoldást mutatjuk. A Gábor-féle elrendezésben síkhullámot használunk mint referenciát, a Fourier-elrendezésben pedig egy pontszerű forrásból kifutó gömbhullámot.
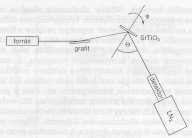
2.
ábra. Az
atomi felbontású hologrammok készítésére
használt mérési elrendezés vázlata.
A röntgenforrásból jövő fotonok
egy grafit monokromátorra esnek, amely kiválasztja
a Sr- atomok gerjesztéséhez szükséges
energiát. A detektor egy vízszintes körön
mozog és a síkminta saját tengelye körül
forog. E két mozgás együttesen a detektor félgömbön
való mozgatását imitálja.
A sugárzás megjelenhet elektronhullám (például Auger- vagy fotoelektronok) vagy elektromágneses hullám (fluoreszcens sugárzás) formájában. Ezeket a folyamatokat felhasználva egyszerre megoldódik a hullámhossz és forrásméret probléma. Részletes elméleti megfontolások után kiderül, hogy az elektronok használata a megfigyelhetőség szempontjából kedvezőbb. Ennek oka, hogy az elektronok atomokkal való kölcsönhatása nagyságrendekkel erősebb, mint a fotonoké, így a hologramban megjelenő intenzitás-oszcillációk is sokkal nagyobbak. Nem csoda tehát, hogy először elektronokat használtak atomok holografikus leképzésére [3].
Ezen a ponton a figyelmes olvasó megkérdezheti,
miképpen tudunk a makroszkopikus minta sok atomjából
pontosan egyet kiválasztani és arra késztetni,
csak ő maga sugározzon és a többi atom
ne. Nos a kérdés jó, és a válasz
az, hogy gyakorlatilag nem lehetséges egy atom kiválasztása
mint forrásé. Mit tehetünk ekkor? A megoldást
egy speciális minta választása adja. Olyan
mintát kell készíteni, amelybe minden forrásatom
ugyanazt a hologramot és ugyanoda hozza létre. Ezek
a feltételek egy egykristály minta esetén
teljesülnek, hiszen egy meghatározott krisztallográfiai
pozícióban elhelyezkedő atomok környezete
azonos. Ha a minta méretéhez viszonyítva
távol helyezzük el a detektáló felületet,
akkor az egyes atomok által létrehozott hologramok
ugyanarra a helyre esnek. Az elektronokkal végzett kísérletek
egyértelműen bizonyították a belső
forrás elvének helyességét. De mint
minden elektronok számlálásán alapuló
technika, ez is csak nagyvákuumban végezhető,
és csak a felületközeli rétegekről
ad információt az elektronok kis szabad úthossza
miatt. Ezért igen hasznos lenne, ha elektromágneses
hullámokkal, azaz röntgensugárzással
is végre lehetne hajtani a kísérletet. Bár
az elektronokkal felvett első hologram 1990-ben készült
és azóta is sok ilyen kísérletet végeztek,
az elvben ugyanúgy működő röntgenholográfia
nem fejlődött ki. Ennek oka a fotonoknak az atomokkal
való viszonylag gyenge kölcsönhatása.
Ez két zavaró effektusban nyilvánul meg:
1. a holografikus oszcilláció igen kis amplitúdójú
(kicsi a jel/zaj viszony), 2. a hosszú távú
transzlációs szimmetria (kristályos rend)
és a fotonok nagy szabad úthossza miatt erős
diffrakciós csúcsok (Bragg-reflexiók) jelennek
meg. Ezek a tényezők évekig megakadályozták
a röntgenhologramok felvételét.
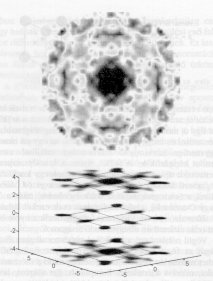
3. ábra.
Felső ábra,
a SrTiO3 röntgen hologramja. Alsó ábra
a hologramból rekonstruált kép.
A megoldás végül is két oldalról történt: egyrészt megmutattuk, hogyan lehet elválasztani a forráshoz közeli és távoli atomok járulékát, kiszűrve ezzel a Bragg-csúcsokat [4], másrészt egy olyan mérési elrendezést hoztunk létre, amely optimális az effektus kimutatására. Az elrendezést a 2. ábra mutatja. A működés röviden a következő: A röntgenforrásból kilépő több energiát tartalmazó sugárzás egy monokromátorra esik, amely kiválasztja a mintában lévő atomok gerjesztéséhez szükséges energiájú fotonokat. Ez azt jelenti, hogy nagyobb fotonenergiát kell választanunk, mint a kilökni kívánt elektron kötési energiája. A nyaláb ezután a mintára esik egy tetszőleges, de a mérés során rögzített szögben. Így a mérés ideje alatt a mintában folytonosan keletkeznek gerjesztett atomok, melyek csak nagyon rövid ideig léteznek ebben a magas energiájú állapotban, mivel a kilökött elektronok helyére a külső héjakról elektronok "esnek be". Az eközben kibocsátott fotonok energiája megegyezik a két atomi nívó energiakülönbségével. Ezeket a fluoreszcens fotonokat használjuk a hologram létrehozására.
A kibocsátott fotonok két úton
juthatnak el a detektorba: 1. a minta valamely atomján
való szóródás után (tárgy
nyaláb), 2. a többi atommal való kölcsönhatás
nélkül (referencia nyaláb). A detektorral letapogatva
a különböző irányokban mérhető
fluoreszcens intenzitást, vagyis a két hullám
interferenciájának eredményét: a forrást
környező atomok hologramját mérhetjük.
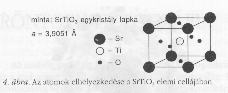
4. ábra. Az
atomok elhelyezkedése a SrTiO3
elemi cellájában
Anélkül, hogy a kísérlet
további részleteibe bocsátkoznánk,
bemutatjuk a végső mérési eredményt.
A 3. ábra felső részén egy
stroncium-titanát (SrTiO3)
egykristályban található Sr-atomok körüli
többi Sr-atom hologramja, az alsó részen pedig
az ebből kapott 3D valós térbeli kép
(tehát atomi rend) látható [5]. Miért
választottuk a SrTiO3-at?
Egy új módszer működését
úgy lehet legvilágosabban bemutatni és meggyőzően
bizonyítani, ha egy jól ismert, egyszerűen
áttekinthető szerkezetben található
atomi rendet képezzük le. A SrTiO3
ilyen. A kristályszerkezet perovszkit típusú,
amelyben a Sr-atomok egy kockarács (egyszerű köbös)
csúcsain helyezkednek el (4. ábra). Mivel
a Sr-atomok szórása sokkal erősebb, mint
a Ti vagy O-atomoké, első közelítésben
csak ezeket látjuk a 3. ábra alsó
részén. Világosan felismerhetők a
nyolc elemi cella csúcsaiban elhelyezkedő Sr-atomok.
Végül néhány szó a jövőről.
A módszer alkalmazhatóságát az fogja
megszabni, hogy mennyire rutinszerűen lehet méréseket
végrehajtani. Jelenleg mind a méréstechnika,
mind a kiértékelés komplikált. Ezt
tükrözi, hogy SrTiO3-on
végzett mérésünkön kívül
mindössze egy hasonló kísérlet történt
a világon, mégpedig hematit (Fe2O3)
kristályon [6]. Tehát az első feladat több
ilyen kísérlet végrehajtása különböző,
de jól ismert anyagokon és az ezekből szerzett
tapasztalatok alapján egy egyszerű és biztonságos
mérési elrendezés és kiértékelési
eljárás kidolgozása. Érdemes-e végigjárni
ezt a nem buktatók nélküli utat? Milyen előnyöket
nyújthat e módszer? Nos, ezt nehéz előre
megmondani, hiszen a megoldható problémák
leggyakrabban akkor jelennek meg, amikor egy módszert
használni kezdünk. Néhány alkalmazást
azonban már most is megjósolhatunk. Ilyenek: 1.
hagyományos diffrakciós mérések kiértékelésénél
segítséget nyújthat a fázisok rögzítésére,
így meggyorsítva és biztosabbá téve
a szerkezetmegoldást, 2. alacsony koncentrációban
jelen lévő szennyező atomok környezetének
vizsgálata, 3. atomi rend meghatározása félvezetőkben
található adalékatomok körül, 4.
biológiai molekulák aktív helyein ülő
fém atomok környezetének feltérképezése
stb. Ezek a problémák megoldhatók a jelenleg
rendelkezésre álló technikai eszközökkel.
Ha egy kicsit távolabbi jövőbe tekintünk,
további érdekes alkalmazásokat láthatunk.
Nagyon erős röntgenforrások és gyors
detektorok használata gyors számítógépes
adatfeldolgozással kombinálva lehetővé
teheti, hogy egy hologramot ms időskálán
vegyünk fel, így valós időben követhetjük
a lassú atomi mozgásokat. Egy további lehetőség,
hogy az atomi fluoreszcencia helyett az atommagokból kibocsátott
gamma-sugárzást használjuk, mint "megvilágító"
nyalábot. Ez olyan előnyökkel jár, mint
kisebb forrásméret és ezáltal jobb
térbeli felbontás, érzékenység
az anyag belsejében kialakult mágneses és
elektronos terekre. Ezek eléréséig azonban
még sok technikai és elméleti problémát
kell megoldanunk.
Irodalom
- D. GABOR - Nature (London) 161 (1948) 777-778
- A. SZŐKE: Generation and Applications, in Short Wavelength Coherent Radiation, ed. by D. T. Attwood and J. Boker AIP Conference Proceedings No. 147 (1986) 361-367 (American Institute of Physics, New York, N. Y.)
- G. R. HARP, D. K. SALDIN, B. P. TONNER - Phys. Rev. Lett. 65 (1990) 1012-1015
- M. TEGZE, G. FAIGEL - Europhys. Lett. 16(1991) 41-46
- M. TEGZE, G. FAIGEL - Nature 380(1996) 49
- T. GOG ET AL. - Phys. Rev. Lett. 76(1996) 3132