Fizikai Szemle honlap |
Tartalomjegyzék |
közölte: Honyek Gyula

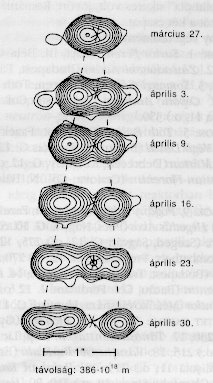
A közös centrumtól távolodó két
objektum látszólagos szögsebességét
könnyen meghatározhatjuk, ha látószögüket
az idő függvényében ábrázoljuk
és a kapott egyenesek meredekségét leolvassuk.
Ha 1-es index jelöli a baloldali, 2-es index pedig a jobboldali
forrást, akkor 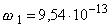 rad/s, illetve
rad/s, illetve
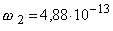 rad/s értékekre
jutunk.
rad/s értékekre
jutunk.
A rádióforrások 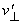 transzverzális
(keresztirányú) sebességét a szögsebesség
és az R = 12,5 kpc = 3,86 x 1020 m
távolság szorzataként számíthatjuk
ki:
transzverzális
(keresztirányú) sebességét a szögsebesség
és az R = 12,5 kpc = 3,86 x 1020 m
távolság szorzataként számíthatjuk
ki:
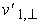 = 3,68 · 108
m/s = 1,23 c,
= 3,68 · 108
m/s = 1,23 c,
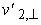 = 1,88 · 108 m/s
= 1,88 · 108 m/s 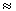 0,63 c,
ahol c a fénysebesség.
0,63 c,
ahol c a fénysebesség.
Egyszerű számításaink alapján
arra a meglepő eredményre jutottunk, mintha a baloldali
objektum fénynél sebesebben mozogna. A probléma
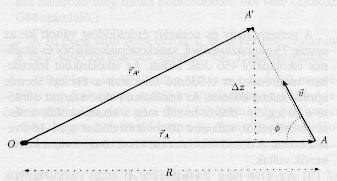
feloldása érdekében képzeljünk
el egy fényforrást, ami v sebességgel
mozog egy tőle távoli O megfigyelő
irányához képest 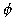 szögben (ábra).
A sebesség nagyságát jelölje
szögben (ábra).
A sebesség nagyságát jelölje 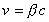 A fényforrás távolságát a megfigyelő
R-nek méri, szögsebességét
A fényforrás távolságát a megfigyelő
R-nek méri, szögsebességét 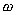 -nak
észleli. Tekintsük a forrás mozgását
-nak
észleli. Tekintsük a forrás mozgását
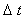 ideig, miközben az A pontból az A'
pontba jut:
ideig, miközben az A pontból az A'
pontba jut: 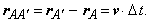
Jelölje 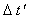 az A-ból, illetve A'-ből
induló jelek beérkezésének időbeli
különbségét az O pontban. Mivel
A és A' távolsága különböző,
a fénysebesség pedig véges:
az A-ból, illetve A'-ből
induló jelek beérkezésének időbeli
különbségét az O pontban. Mivel
A és A' távolsága különböző,
a fénysebesség pedig véges: 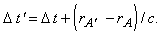 . Kis
. Kis 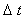 idők esetén
idők esetén 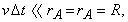 azaz
azaz 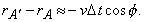 Mindezek figyelembe vételével:
Mindezek figyelembe vételével:
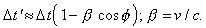
Így a forrás O-beli látszólagos keresztirányú sebessége
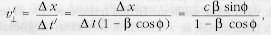
ahol felhasználtuk, hogy a megfigyelő vonatkoztatási
rendszerében a valódi keresztirányú
sebesség 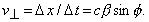 Az O-ban észlelhető
szögsebesség:
Az O-ban észlelhető
szögsebesség:
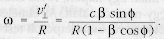
Ha feltételezzük, hogy a két objektum egy egyenes mentén, azonos nagyságú sebességgel távolodik egymástól (a részletes olimpiai feladat ezt mondta ki), akkor a következő összefüggéseket írhatjuk fel a látszólagos szögsebességekre:
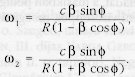
A megadott, illetve mért numerikus értékek
segítségével a fenti két kifejezésből
egyszerű algebrai átalakításokkal 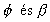 értéke kiszámítható:
értéke kiszámítható: 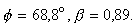 Megnyugodhatunk
tehát, hiszen az észlelt rádióforrások
mindössze a fénysebesség 89 %-ával mozognak.
Megnyugodhatunk
tehát, hiszen az észlelt rádióforrások
mindössze a fénysebesség 89 %-ával mozognak.
Érdekességként megjegyezzük, hogy a látszólagos keresztirányú sebesség akkor lehet nagyobb a fénysebességnél, ha a következő feltétel teljesül:
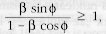
ami a vizsgált esetben fenn is áll. Könnyen
meggyőződhetünk arról, hogy ennek a
kifejezésnek a fizikailag értelmes szögtartományban,
adott 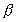 esetén akkor van maximuma,
ha
esetén akkor van maximuma,
ha 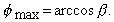 Eszerint
a látszólagos keresztirányú sebesség
végtelenhez tarthat, ha
Eszerint
a látszólagos keresztirányú sebesség
végtelenhez tarthat, ha 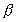 egyhez tart, ami persze azt
is jelenti, hogy
egyhez tart, ami persze azt
is jelenti, hogy 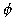 nullához tart, vagyis a mozgó
objektum a megfigyelő felé mozog közel fénysebességgel.
nullához tart, vagyis a mozgó
objektum a megfigyelő felé mozog közel fénysebességgel.