Fizikai Szemle 1999/5. 210.o.
HUNGARIAN PHYSICISTS ENTERING BIOLOGY
Tamás Vicsek
Department of Biological Physics
Eötvös University, Budapest
During the first decades of this century a new generation of outstanding Hungarian scientists appeared who devoted their life to physics or physics related research. Several of them were given Nobel Prize, but the rest also made important contributions to the advancement of natural sciences. There was a particular group within this stream of researchers whose members started their activities as physicists, but later turned to biology or physiology where they applied with great success their physics background to solve problems in life sciences.1
George de Hevesy, who had previously been an assistant of Lord Rutherford, the discoverer of the atomic nucleus, was recommended by Roland Eötvös in 1917 to be a professor and the bead of the Institute for Applied Physics in Budapest. Hevesy started to organize his laboratory for studying radioactivity. However, soon politics came into play and after the World War I the classically trained Eötvös epigons and other colleagues matring use of the changing political atmosphere achieved that Hevesy was deprived of his professorship for having been appointed by "suspicious communist sympathizers" like Theodore von Kármán.
Hevesy then accepted the invitation by Niels Bohr to organize a nuclear laboratory in Copenhagen. At that time he had got the idea of using radioactivity as a tracer in biology. The naturally radioactive elements (close to the end of the Periodic Table) could not serve for this purpose because they do not take active part in relevant biological processes and are toxic. Thus, he developed neutron activation of elements essential from the point of life and produced, for example, radiophosphorus. In this way he could study the metabolism of phosphorus, among others in the energy carrier molecule called ATP and in the genetic material (DNA). In 1943 he was awarded the Nobel Prize in chemistry "for his work on the use of isotopes as tracers in the study of chemical processes". In a way, his work can be looked as application of physical/chemical processes to essential phenomena in biological systems.
The life and work of another Hungarian scholar was also devoted to the understanding of physiological processes using approaches borrowed from physics. George von Békésy obtained his Ph.D. in Physics in Budapest (1923) and worked in the telecommunication engineering laboratory of the Hungarian Postal Service. The laboratory of the Hungarian Telephone Service was well equipped. However, many complains arrived from abroad about the poor quality of the long distance telephone lines going through Budapest. Békésy, the youngest assistant was given the job to correct the problem. He discovered that the clicks during connections and disconnections contained many frequencies and by analyzing these he could give a better diagnostics of the whole network.
To better understand the whole system, he started to investigate the perhaps most important component of it, the human ear. The functional similarity of the phone membrane and the ear drum led him to study the specific parts of the ear. He showed that Helmholtz's theory of hearing was wrong because it was not the eigenvibrations of the cilia (ear filaments) which played the key role in hearing. Instead, the vibrations of the cochlea (ear fluid) are decisive in sensing the frequency of sounds. He was promoted to be a professor at the University of Budapest in 1943 and was given a Nobel Prize for his "discoveries concerning the physical mechanism of stimulation within the cochlea" in 1961.
Hungarian scientist will celebrate the 100th anniversary of the birth of George von Békésy this June.
Interdisciplinary research was also typical for another Hungarian Nobel Prize winner, Albert Szent-Györgyi, who received his award in physiology for his discoveries in connection with the biological combustion processes with special reference to vitamin C and the catalysis of fumaric acid" (1937). He was maroly interested in the biochemical oxidation: how the transfer of an electron from one molecule to another supply a cell with energy. Trained in medicine, he later turned to physics, learned a great deal of quantum mechanics so that he could better describe the transport of electrons in biological molecules.
A remarkable example of an outstanding Hungarian physicist entering biology is Leo Szilard. He had obvious talent in physics already being evident during his high school years when he won first prize in physics in the Eötvös Student Competition. Soon he enrolled in the Budapest Institute of Technology to study mechanical engineering. After the World War I he had to leave Hungary and continued his studies at the Berlin Institute of Technology. There, inspired by the presentations of greatest figures of physics during the 20s, including Einstein, Laue, Nerst and Planck, he became a graduate student in physics. He preferred attending laboratories and seminars instead of regular lectures and when Planck recommended to take courses in theoretical physics Szilard
responded: "I only want to know the facts. I will make up the theories myself". He was interested in statistical thermodynamics and made seminal contributions to information theory. Later, in the early thirties he discovered the principle of nuclear chain reaction, having a significant impact on the whole 20th century. However, he never received a Nobel Prize; he was too unusual, ever changing, sparkling with excellent ideas, but typically not devoting enough time to pursue his ideas himself to a level corresponding to a well established, completed research.
After the World War II he felt that modern biology could be the right territory for him to explore his talent. A vast amount of data on the living matter had accumulated, new, subtle experimental techniques had been developed, so it was time for him to discover unifying principles. Szilard became a professor of biophysics in Chicago. He developed the chemostat which can be used to provide a closed, steady environment for bacterial reproduction under complete physical and chemical control. In his chemostat hundreds of generations of bacteria could be observed as mutations, natural selection, and evolution took place during a long experiment. In 1954 Newsweek reported that "here for the first time, as the bouncy, smiling physicists remarked, evolution has been made visible".
He had many more inspiring ideas about biological processes. Several of these led eventually to very successful research. In particular, following a suggestion by Szilard, Jacques Monod explored the enzyme repressor mechanism in cells and was given a Nobel Prize for this work on this occasion he expressed his thanks to Leo Szilard for the guiding idea in his Nobel lecture (1965).
It follows from the above that research along the borderline of physics and biology has a great tradition in Hungary. Indeed, there are many successful biophysical schools in our country. Some of these are embedded into a biology/medical environment. Examples include Biophysics Institutes/Departments in Budapest (where, in the Semmelweis Medical University the Biophysics Institute was established about 50 years ago by a leading physicist, Imre Tarján), Debrecen and Pécs. On the other hand, there are also places where many of the leading scientists have a dominantly physics background. Szeged plays a special role in this respect: in the Biological Center the directors of the Biophysics Institute have been physicists (Lajos Keszthelyi, Pál Ormos) entering biology. Their activity had an essential impact on the widely acknowledged research carried out in the institute in such areas of biophysics as Membrane Bioenergetics, Molecular Neurobiology, Membrane Structure and Dynamics, Microbial Gas Metabolism, Stress Physiology and Transport in Plants. In addition, there are excellent groups at the University of Szeged led by physicists (Zsolt Bor, Péter Maróti) and doing biophysics research. In Budapest there is a physicists dominated (Péter Érdi, Zsolt Szőkefalvi-Nagy) biophysics group in the Particle and Nuclear Research Institute and in 1998 the Institute for Physics at the Eötvös University created a Biological Physics Department (growing out from a group in the Atomic Physics Department) led by Tamás Vicsek.
After the above brief overview of the historic contributions of Hungarians to results on phenomena involving both physics and biology and giving a partial list of the present activities, in the second part of this article I would like to concentrate on a few selected topics which have been the subject of recent research in my group at the Department of Biological Physics. These investigations are all closely related to statistical physics; in a way they demonstrate how the ideas common in the theory of phase transitions and fluctuations can be applied to biology.
Recent discoveries in biology have motivated an increasing number of physicists to study biologically inspired problems. It has turned out that the methods developed by physicists can be very useful in making the investigations in life sciences more quantitative. In turn, there is a growing interest in the biology community to present and interpret their findings by using the advanced hardware and the numerical and theoretical techniques developed by physicists.
In particular, during the last decade the well established tools of statistical physics have been successfully applied to an increasing number of biological phenomena. This has been in part due to a breakthrough in statistical physics. In simple terms, statistical physicists have been able to theoretically establish that physical systems consisting of a large number of interacting particles obey universal laws that are independent of the microscopic details. The concepts are so general that they can be applied to a broad class of systems even beyond physics.
Statistical physics is a useful approach to the investigation of a system if it has many identical (or nearly identical) units or/and the random perturbations play an important role. There are many such systems in biology, for example, the number of individuals in a group of organisms or the codons in a genetic code can be very large, and the behavior of the macromolecules (e.g. molecular motors) is largely influenced by the thermal fluctuations.
Collective motion.
The collective motion of organisms (birds, for example), is a fascinating phenomenon many times capturing our eyes when we observe our natural environment. In addition to the aesthetic aspects of collective motion, it has some applied aspects as well: a better understanding of the swimming patterns of large schools of fish can be useful in the context of large scale fishing strategies.
Our goal is to describe the collective motion of organisms in the presence of fluctuations. Therefore, we introduced biologically inspired, inherently non-equilibrium models consisting of self-propelled particles. In our models the particles corresponding to organisms locally interact with their neighbours by choosing at each time step the local average velocity with some perturbation added to take into account the fluctuations always present in a biological system.
In the limit of vanishing velocities the models are analogous to Monte-Carlo realizations of equilibrium ferromagnetic systems. The analogy is as follows: the Hamiltonian tending to align the spins in the same direction in the case of equilibrium ferromagnets is replaced by the rule of aligning the direction of motion of particles, and the amplitude of the random perturbations can be considered proportional to the temperature. Our numerical simulations indicate the existence of new types of transitions. Depending on the control parameters both disordered and long-range ordered phases can be observed, and the corresponding phase space domains are separated by singular "critical lines". In particular, we demonstrated both numerically and analytically that there is a disordered to ordered motion transition at a finite noise level even in one dimension.

Fig. 1. In this figure the velocities of the particles ("birds") in the model for the collective motion of organisms are displayed for varying values of the density and the noise. The actual velocity of a particle is indicated by a small arrow, while their trajectory for the last 20 time step is shown by a short continuous curve. The number of particles is N= 300 in each case. (a) The initial 20 time steps. (b) After some time, for small densities and noise the particles tend to form groups moving coherently in random directions, (c) for higher densities and noise the particles move randomly with some correlation, (d) for higher density and relatively small noise the motion becomes ordered.
In the case of equilibrium systems possessing continuous rotational symmetry the ordered phase is destroyed at finite temperatures in two dimensions, where we also observe ordering. Thus, the question of how the ordered phase emerges due to the non-equilibrium nature of the model is of considerable theoretical interest as well. From a hydrodynamical point of view, in SPP systems the total momentum is not conserved. Thus, the flow field emerging in these models can considerably differ from the usual behavior of fluids.
The above described studies have led to a much deeper insight into the dynamics of flocking.
Molecular motors.
The origin of biological motion can be traced back to the function of molecular motor proteins. Cytoplasmic dynein and kinesin transport organelles within our cells moving along a polymeric filament, the microtubule. The motion of the myosin molecules along the actin filaments is responsible for the contraction of our muscles. Recent experiments have been able to reveal some important features of the motion of individual motor proteins, and a new statistical physical description - often referred to as "thermal ratchets" - has been developed for the description of motion of these molecules. In this approach the motors are considered as Brownian particles moving along one-dimensional periodic structures due to the effect of non-equilibrium fluctuations.

Fig. 2. Demonstration of the ordering in the model collective motion in which the "birds" are trying to follow each other in the presence of perturbations. Snapshots of the time development of a system consisting N= 4000 particles are shown after (a) 50, (b) 100, (c) 400 and (d) 3000 Monte-Carlo steps. First the behavior is reminiscent of the equilibrium XY model, where the long range order is missing since vortices are present in the system. However, due to the motion of the particles, the vortices are unstable, and finally a self organized longrange order develops.
Recently individual two-headed kinesin molecules have been studied in in vitro motility assays revealing a number of their peculiar transport properties. We have proposed a simple and robust model for the kinesin stepping process with elastically coupled Brownian heads showing all of these properties. The analytic and numerical treatment of our model results in a very good fit to the experimental data and practically has no free parameters. Changing the values of the parameters in the restricted range allowed by the related experimental estimates has almost no effect on the shape of the curves and results mainly in a variation of the zero load velocity which tan be directly fitted to the measured data. In addition, the model is consistent with the measured pathway of the kinesin ATPase.
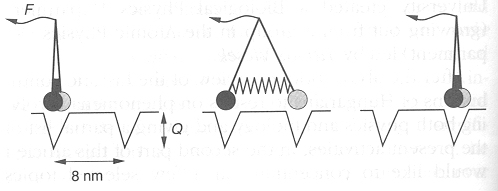
Fig. 3. Schematic representation of the stepping process of the kinesing molecule along a microtubule. The interaction of the kinesin heads with the microtubule is modelled by a periodic, locally asymmetric potential. In each step an ATP molecule is consumed leading to a morphological change represented by the stretching and a subsequent relaxation of an imaginary spring between the heads.
Assuming specific types of interaction between the particles the models tan be made more realistic. In addition to the motion of the kinesin molecules, we have worked out the theory of such further molecular motors as the acto-myosin system and the ATP synthase (the smallest rotary motor in nature).
Distribution of cell velocities in cultures.
Because of the great complexity of a cell there is always a considerable diversity in the behavior of individual cells. Accordingly, one of the most relevant questions addressed for such systems is the corresponding distribution, i.e. the number of cells with a given value of the parameter considered. In particular, the motility and the mechanism of migration of cells have attracted great interest recently because of their relevance to a number of important processes, including the development of the nervous system, immune reactions and tumor spreading.
We have measured the in vitro velocities of two kinds of tissue cells using time-lapse video microscopy. In order to obtain data providing a good basis for a careful statistical analysis we have developed a computer controlled system which automatically collects data and maintains the conditions necessary for the cells' activity for several days in a small chamber attached to the microscope. Our large data set indicates that - in contrast to the widely assumed Gaussian - the locomotion activity displays an exponential distribution. Thus, in spite of the extremely complex cellular processes, the motion of an ensemble of cells tan be well described by a simple universal distribution function suggesting robust statistical properties of the cellular processes.
Indeed, the experimental observations tan be explained in terms of a phenomenological model incorporating the interaction of various cellular processes and the effect of finite ATP production rate. There is a formal similarity between the exponential distribution of the cells' velocities and the Boltzmann energy distribution within systems in thermal equilibrium. In the latter case, the uniform microcanonical distribution tan be derived using either quantum mechanics or Liouville's theorem for Hamiltonian systems while here it is an interesting feature of the interacting regulatory processes. By using a statistical physics based approach to the description of how the available energy is distributed among the many simultaneous regulatory processes within a cell we have been able to relate our experimental findings to these processes and get an insight into a cell's energy management.
Correlations in DNA sequences.
DNA molecules are the most sophisticated information databases created by nature through the dynamic process of evolution. The information necessary for the reproduction of organisms is stored in the form of a sequence which tan be considered as a long series of four "letters" (T, G, C, A) corresponding to the four bases in DNA molecules. While a mechanism of encoding some of this information is understood (for example, the genetic code directing amino acid assembly, sequences directing intron/exon splicing, etc), relatively little is known about other layers of information encrypted in a DNA molecule. In the genomes of high eukaryotic organisms, only a small portion of the total genome length is used for protein coding. The role of introns and intergenic sequences constituting a large portion of the genome remains unknown.
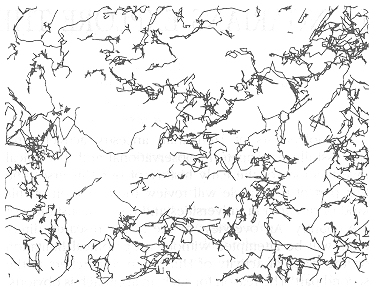
Fig. 4. This figure shows how the trajectories of cells look like during the first 20 hours in a culture of neuronal progenitor cells (NE-C4). The trajectories were determined by videorecording the motion of the cells followed by a digital image processing of the data.
In recent years sequence data have been collected through the joint effort of many research laboratories working within the framework of the Human Genome Project. In the near future, the amount of information is expected to increase by several orders of magnitude. It is generally accepted that the structure of DNA is very complex, heterogeneous, and cannot be described by any single mathematical model. A new science Computational molecular biology starts to crystallize out of these methods and models.
A possible approach to uncovering the information stored in the symbol sequence corresponding to a DNA molecule is to regard it as a written text composed by using four letters. Naturally, we do not know the "language" of the text, thus, when we are trying to get information about the sequence as a whole we are led to apply methods developed for analyzing written (natural) texts of unknown origin. In a recent related method distances between series of symbols are characterized by the dot products of vectors corresponding to the given sequences. This distance (measure), depending on the local and short-range properties of the sequences, reveals the different nature of coding and non-coding elements of the genome.
In this article I have tried to briefly overview both the famous, already historic cases of Hungarian physicists contributing to the advancement of biology and a small selection of very recent efforts in which the ideas borrowed from statistical physics have been helpful in gaining a better understanding of some biological systems.
____________________
Their stories have been thoroughly accounted for in an interesting recent monograph by George Marx titled "The Voice of the Martians" I used this book as a source when writing the first part of this article
.



