AKTÍV SOKRÉSZECSKE-RENDSZEREK CSODAVILÁGA

Dirk Helbing
Stuttgarti Egyetem II. Elméleti Fizikai Intézete,
Collegium Budapest

Hogyan szerveződnek a madárrajok és miben hasonlítanak a spin-rendszerekhez? - Miért bénítják meg gyakran a gépkocsiforgalmat olyan dugók, amelyek látszólag “a semmiből" alakulnak ki? - Miért “halad" néha a forgalom megállások és újraindulások végeláthatatlan sorozataként? - Miért alakul ki oly gyakran forgalmi dugó jóval azelőtt, hogy a járművek sűrűsége elérte volna az út átbocsátó kapacitását? - Elképzelhető-e, hogy a járművek számának csókkenése is eredményezheti dugók kialakulását? - Alkalmasak-e sebességkorlátozások a forgalom intenzívebbé tételére? - Szemben haladó gyalogosok forgalma miért szerveződik sávossá? - Törvényszerű-e, hogy önszerveződő rendszerek önmaguktól is optimálissá alakítják állapotukat? - Hogyan megy végbe az, amikor pánikba esett menekülő gyalogosok végzetes blokkoló tömörüléseket alakítanak ki? - Van-e hasonlóság a közlekedésben tapasztalt, jelenségek és a tőzsdei piacalakulások dinamikája között? Az önhajtott részecskerendszerek dinamikájának újabban elért jobb megismerése közelebb hoz a fent, felsorolt problémák nagy részének megértéséhez. [1]

A klasszikus mechanikában gyakran van dolgunk Newton mozgásegyenletével, amely egy m_i tömegű test gyorsulását más (például j indexszel azonosított) testekkel való, párkölcsönhatás erői együttes hatásának tekinti.

Az kölcsönhatási erők elsősorban attól függenek, hogy hol tartózkodnak az i és j kölcsönható testek tömegközéppontjai a t időpontban: (x_i(t) és x_j(t), sőt gyakran mindössze attól, hogy mekkorák a d_ij = (x_j - x_i) távolságvektorok. Speciális esetekben viszont attól is függenek, mekkorák és sebességek. Potenciálerők hatása esetében - például a klasszikus csillagászatban - a rendszer Hamilton-függvénnyel jellemezhető.

Meghajtott sokrészecske-rendszerek leírásánál (például az olyan folyadékok vizsgálatánál, amelyekben nyomásgradiensek hatnak) a fenti egyenlet további (erő-) tagokkal kell kiegészíteni. Ilyenek: (külső) f₀ (x,t) meghajtó erők, valamint súrlódási erők (itt a mennyiségek súrlódási együtthatók). Szükség lehet még fluktuációk hatásának figyelembe vételére is. Mindennek végeredménye egy

  (2)

Hasonló a helyzet rázott, vagy a nehézségi erő hatására gyorsuló szemcsés anyagok viselkedésének leírásánál.

A meghajtó erők és a disszipatív súrlódási erők versengése során az energiák időben és térben átrendeződnek, ez pedig sokféle önszervezési folyamat megindulásával és mintázatok kialakulásával járhat együtt. Így például meghajtott folyadékokban instabilitások figyelhetők meg, ezeknek eredményeképpen pedig komplex mozgási mintázatok vagy turbulenciák jöhetnek létre: Függőleges csőben eső homokban sűrűségi hullámok alakulnak ki [2]. Rezgetett szemcsés anyagokban hasonló konvekciós mintázatok figyelhetők meg, mint hevített folyadékokban [3], sőt fémgolyók rezgése kollektív oszcillációk gerjesztésével is együtt járhat.

A (2) egyenletet csekély mértékben általánosított formában fogjuk használni. A hagyományos fizikai rendszerek tárgyalásától eltérően feltesszük, hogy “önhajtott", "aktív" vagy “motorizált" (tehát belső energiával rendelkező) részecskék alkotják a rendszereinket [5]. Emiatt az kölcsönhatási erőkre már nem mindig érvényes Newton harmadik = - (hatás = ellenhatás) törvénye. Ezen felül a részecskékre hathatnak az általános helyett az egyenletekbe beírandó egyéni meghajtó erők. Ebből számos érdekes jelenség létrejötte vezethető le és ezek a jelenségek az élő világban (például biológiai vagy társadalmi-közgazdasági rendszerekben) meg is figyelhetők.

Célszerű átírni a (2) egyenletet:

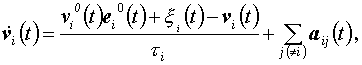     (3)

itt 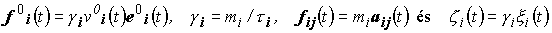. Az a_ij(t) gyorsulásokat - kissé pongyolán - általánosított erőknek is szokás nevezni.

A (3) egyenletből kiolvasható, hogy amennyiben egy i részecske elég távol van a többi j részecskétől, a meghajtási, fluktuációs és súrlódási- tagok együtt a részecskesebességek exponenciális közelítését eredményezik () relaxációs időállandóval) egy v⁰_i egyensúlyi sebességhez, amelynek zajszintjét -vel jelöljük. Amennyiben a (gyors relaxáció) határesettel van dolgunk, a túlcsillapított

  (4)

egyenletet kapjuk, ahol = és és . Az alábbiakban feltételezzük, hogy az f _ij kölcsönhatási erők kis hatótávolságú taszító erők.

Cikkünk további részeiben elsősorban az fog bennünket érdekelni, hogy önhajtott sokrészecske-rendszerekben milyen jelenségek milyen feltételek mellett léphetnek fel. A szemléletesség érdekében közismert, mindennapi jelenségek példáit fogjuk elemezni. Nem akarjuk elhallgatni, hogy az elemzéseink tárgyát képező rendszerek a valóságban több vonatkozásban is lényegesen bonyolultabbak, semhogy matematikai modellekkel kimerítően jellemezhessük azokat. Nem csoda tehát, hogy részletesebb leírásukkal (a fizika mellett, illetve előtt) más tudományok is foglalkoztak.

Madárrajok és spinrendszerek

Feltételezzük, hogy rendszerünk minden i részecskéje azonos és állandó sebességgel "repül" és hogy v_ij (t) = 0. Ekkor a (4) egyenlet leegyszerűsödik az

egyenletté, amelyet a

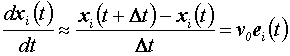
egyenlettel együtt kell megoldani. A fluktuációkról feltételezzük, hogy csak e⁰_i(t), illetve e_i (t) irányát módosítják, mégpedig átlagosan annál erősebben, minél nagyobb az fluktuációs intenzitás. Az vektor tehát normált. Azt is feltételezzük, hogy a haladás e⁰_i (t) irányai válaszidővel hozzáigazodnak a lokális i átlagos haladási irányhoz:

,  (5)

ahol a átlagolást jelöl mindazon j részecskékre, amelyek x_i körüli R sugarú gömbön belül tartózkodnak, az N (y) = y / |y| függvény pedig a haladási irányt normálja.

1. ábra. Madár-, illetve spinszerűen kölcsönható részecskék háromféle rendezettségi állapota, illetve viselkedése periodikus háromdimenziós térben. Úgy látszik, csak az számít, hogy mekkora a részecskék sűrűsége () és a fluktuáció erőssége (), valamint az, mozognak-e a részecskék vagy nem. Ugyanakkor pedig a részecskék sebessége csak az eredményes önszervezéshez szükséges időtartam hosszát befolyásolja. A sötét színben ábrázolt terület a ferromágneses viselkedés tartománya, de madárrajok a szürke tartományban is alakulnak ki, ahol a spinrendszer már nem rendezett. A tartományok közötti határvonalak megfelelnek a , ()kritikus görbéknek.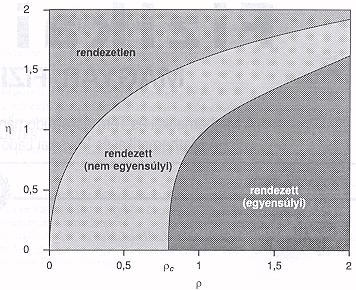

Fenti feltételezésünk - bizonyos fokig - a madarak röptének jellegzetességeit tükrözik [6, 7]. Az ehhez kapcsolódóan elkészített modellünk azzal a feltételezéssel indul, hogy a részecskék kezdeti eloszlása egyenletes és a továbbiakban periodikus peremfeltételekkel számol. A esetben - bármilyen kicsiny is a részecskesűrűség - létezik olyan kritikus fluktuációs intenzitás, amely alatt - még vonzó kölcsönhatási erők v_ij = 0 nélkül is - részecske-csoportosulások alakulnak ki, amelyeken belül az e_i haladási irányok párhuzamosan “álltak be" (1. ábra). Szemléletes megfogalmazásban ez azt jelenti, hogy modellünk szerint, ha a fluktuációk elég kicsinyek, a madarak rajokká szerveződnek, ellenkező esetben pedig rendezetlenül repdesnek (mégpedig annál inkább, minél kisebb a sűrűségük). Az egyensúlyi (v₀, = 0) rendszerünk viszont megfelel egy homogén sűrűségű Heisenberg-féle spinrendszernek, amelyben egy kritikus hőmérséklet alatt - csakúgy, mint ferromágneses anyagban - az e_i spinek párhuzamosan állnak be. (A kritikus hőmérséklet arányos az fluktuációs intenzitással.) A rendezetlen mozgásról a rendezett mozgásra való áttérés feltétele ez esetben azonban az, hogy a részecskesűrűség nagyobb legyen egy bizonyos _c (perkolációs) értéknél (1. ábra). Ezek szerint - meglepetésünkre - alapvetően eltérő viselkedést tapasztalunk a v₀ = 0, illetve esetben [8]!

Végeredményben tehát azt mondhatjuk, hogy önhajtott nem-egyensúlyi rendszerekben a részecskék mozgása hasonlóképpen hat, mint egy hosszú hatótávú kölcsönhatás. Ezért még analóg egydimenziós rendszereknél is a esetben fázisátmenetet tapasztalunk a rendezett állapotba [9], viszont a v₀ = 0 esetben fluktuációk fellépése esetében a rendszerek elvileg rendezetlenek. Ez jó példa arra, hogy egyensúlyi és nem-egyensúlyi rendszerek mennyire drasztikusan eltérő viselkedést képesek tanúsítani.

Semmiből kialakuló országúti dugók

Maradjunk egyelőre az egydimenziós rendszereknél, konkrét problémaként pedig vizsgáljuk az egysávos egyirányú közúti járműforgalom longitudinális dinamikáját. Az e⁰_i haladási irányok ilyenkor mind párhuzamosak.

A járművek (illetve vezetőik) viselkedésének modellezésénél alkalmazott tipikus egyenlet

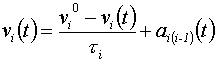  (6)

alakú. Az fékezési gyorsulás a legegyszerűbb esetben csak az s_i (t) = x_i-1 (t) - x_i (t) távolságtól függ, (Természetesen valószínűbb lenne, ha a saját v_i(t) sebességtől és a relatív sebességtől való függésekkel is számolnánk.) A (6) egyenlet egyik jellegzetessége az a feltételezés, hogy az i indexű jármű vezetője - jelen esetben ez tekintendő az aktív részecskének - a mindenkori (előtte haladó) (i-1) járműre “figyelve" reagál; a mögötte haladó jármű viselkedésére való reagálást pedig elhanyagolhatónak tekinti. (Vannak ugyan modellek, amelyek a tényleges reagálást ennél pontosabban veszik figyelembe, azonban ezekben sem érvényes a hatás = -ellenhatás elve.) A továbbiakban először az azonos járművek oszlopának esetét tárgyaljuk, amikor is a fluktuációkat pedig hanyagoljuk el. Ekkor sok esetben célszerű egy

  (7)

“optimális sebességet" definiálni, amelyhez a v_i(t) tényleges sebesség relaxációs idővel közelítve tart.

Amennyiben a V optimális sebesség csak az s_i(t) távolságtól függ, kimutatható, hogy egy egyenletes járműforgalom (azonos sebességű, egymástól azonos távolságokban haladó járművek) kis zavarokkal vagy fluktuációkkal szemben stabil, ha

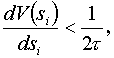  (8)

ellenkező esetben azonban lineárisan instabil [10]. A lineárisan stabil tartományon belül van egy abszolút stabil tartomány, amelyben bármilyen nagy mértékben zavart forgalom is lecsillapodik térben homogén járműáramlássá, valamint egy nemlineárisan instabil (metastabil) tartomány, amely szomszédos a lineárisan instabil tartománnyal [11]. Ez utóbbi metastabil tartományban csak azok a zavarok tűnnek el maguktól, amelyeknek amplitúdói kisebbek egy a sűrűségtől függő “kritikus amplitúdónál"; az ennél nagyobb zavarok pedig tovább növekednek.

A forgalom csak addig stabil, amíg a V(s_i) függvény alig változik az s_i távolsággal, vagyis amíg a járművek sűrűsége kicsiny (“szabad forgalom"), vagy pedig igen nagy (mert ilyenkor a járművek sebessége szükségképpen kicsi). A közepes sűrűségek tartományában (sávonként körülbelül 25 jármű kilométerenként), illetve körülbelül 80 km/óra sebesség alatt) a V(s_i) optimális sebesség erősen csökken a követési távolsággal együtt. Ezért azután a legkisebb zavar (baleset vagy szűkület nélkül is) folyamatosan megnő egészen egy dugó kialakulásáig. Az ilyen, “semmiből keletkező" dugó voltaképpen láncreakció eredménye, amely egyenkénti túlreagálások sorozata. A relaxációs (alkalmazkodási) idő végessége ugyanis azt jelenti, hogy a forgalombeli helyzet változására a járművek vezetői késéssel reagálnak, túl közel kerülnek az előttük haladó járműhöz, emiatt azután túl erősen fékeznek. Ha a következő jármű előbb érkezik, semhogy a túlreagálás kikompenzálása bekövetkezhetett volna, a most leírt folyamat megismétlődik stb., amíg végül is a túlfékezések összegezett és egyre növekvő sorozata a járműoszlop valamelyik tagjának (és követőinek) meg állítását nem eredményezi.

Ami ezen dugó felszámolását illeti, erre azért nem kerül sor, mert a dugónak a haladás irányába eső frontjánál az újrainduló járművek időt veszítenek, vagyis nagyobb időközökben startolva olyan (jármű/óra egységekben kifejezett) Q_ki kiáramlást hoznak létre, amely lényegesen kisebb az egyenletes forgalom mellett maximálisan megvalósítható Q_max-nál, azaz az elméletileg várt útkapacitásnál. Látjuk tehát, hogy a Q_ki is egyfajta “dinamikus útkapacitás", amely lényegében egy önszerveződési folyamat eredményét tükröző forgalmi állandó [12].

A dugók különböző fajtáinak áttekintése

A tapasztalat azt mutatja, hogy legtöbb forgalmi akadály autópályák becsatlakozásai (vagy egyéb szűk keresztmetszetei) “felett" található. Igen jelentős kapacitáscsökkenést (az elméleti Q_max-hoz képest) a forgalom kicsiny (fluktuációszerű) változásai is okozhatnak, ha a csatlakozás előtti Q_be pályaforgalom (az autópálya felől) és a lényegesen kisebb (becsatlakozó út felőli) forgalom összege nagyobb, mint az előző fejezetben bevezetett Q_ki dinamikus kapacitás (2. ábra). A zavart még a forgalom átmeneti csökkenése is kiválthatja. Minden, a kritikus amplitúdónál nagyobb zavar amplitúdója mindenképpen nő. A következő történik: Amíg kicsiny a zavar, a járművekkel együtt azok haladásánál irányában mozdul el, ezért azt remélhetnénk, hogy eltávolodik a kiváltó megzavarás helyétől, majd el is tűnik a rendszerből. A valóságban azonban a járműsűrűség növekedésével egy időben a sűrűség maximumának (a hullámhegynek) sebessége csökken, sőt megfordul, mert a dugó elülső frontján a járművek eltávoznak, hátul azonban újabb járművek olvadnak bele a dugóba. Végeredményben tehát a zavar bumerángszerűen visszajön. Amikor visszaér a becsatlakozás helyére, ott megbénítja a forgalmat, illetve a kapacitást a dinamikus Q_ki értékre csökkenti.

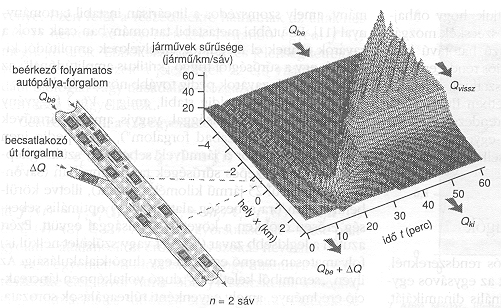
2. ábra. Kétsávos autópálya modellezése. Az autópályára ráhajtó járművek sűrűségének átmeneti csökkenése az x = 0 koordinátájú becsatlakozásánál “bumeráng-jelenséget" vált ki és ez t = 30 perc múlva leblokkolja a becsatlakozási hely előtti forgalmat, ugyanis egy kialakuló és hátrafelé terjedő dugó ekkor és vissza az x = 0 helyre.

Ha tehát a Q_be+ összforgalom nagyobb az autópálya Q_ki dinamikus kapacitásánál, a bumerángszerűen visszatért dugó a becsatlakozás helyén túl is terjed “felfelé" az autópályán, miközben egyre nő. Ezen dugón belüli járműáramlás Q_vissz = Q_ki - .

Mármost [13] öt eset lehetséges (3. ábra): (1) Ha a csatlakozás előtti dugóban a Q_vissz lineárisan stabil, akkor homogén, “lépésben egyenletesen haladó" forgalom alakul ki (tipikus hétvégi dugó). A kisebb értékei mellett Q_vissz lineárisan instabil. Ilyenkor vagy az történik, hogy (2) periodikusan változó sebességű, (1)-nek megfelelő forgalom (“stop-and-slow forgalom") alakul ki, vagy pedig (3) “stop-and-go forgalom", amikor is több dugó található e pályaszakaszon, köztük a “szabad forgalom" szakaszaival. Ebben az esetben minden dugóhullám úgy hozza létre a következőt, hogy egy kicsiny zavart kelt a becsatlakozás helyén, amely először “lefelé" terjed és növekszik, majd (bumeráng!) visszatér a becsatlakozás helyére. Ehhez azonban szükséges, hogy a becsatlakozás
alatt a forgalom lineárisan instabil legyen. Ha viszont metastabil (aminek feltétele a még kisebb forgalom), akkor egy dugóhullám nem tudhat egy következőt kiváltani. Ekkor (4) egyetlen egy dugóhullám fut felfelé a becsatlakozás helye feletti autópályaszakaszon, vagy pedig (5) egyetlen dugó “vesztegel" a becsatlakozás helyén, ami akkor következik be, ha a becsatlakozás feletti szakaszon a forgalom stabil, úgyhogy itt nem futhat visszafelé dugóhullám.

A rohanás célszerűtlensége

Új jelenségek figyelhetők meg, ha többsávos autópályán olyan járművek haladnak azonos irányban, amelyeknek modellparaméterei (v⁰_i , stb.) különbözőek, például személygépkocsik és kamionok. Az előzések és sávváltások nincsenek megtiltva, feltéve, hogy biztonsági szempontból kifogástalan módon hajtják végre (és persze, ha a gyorsabb haladást szolgálják). Modellkísérletek kiderítik - ami várható is - hogy a személygépkocsik gyorsabban haladnak, mint a kamionok, legalább is (1) kis járműsűrűségeknél, valamint (2) közepes sűrűségeknél, amikor a stop-and-go forgalomban akadnak rések, amelyek előzést tesznek lehetővé. Van azonban olyan (keskeny) sűrűségtartomány (közvetlenül a sávonkénti 20 jármű/km felett) amelyben meglepő módon a személygépkocsik nem haladnak gyorsabban, mint a kamionok (4. ábra, baloldalt). Ilyenkor minden jármű - mintha összefüggő tömb része lenne - azonos sebességgel halad [14]. A jelenség magyarázata a következő: Ilyen járműsebességeknél a személygépkocsik amúgy sem haladhatnak sokkal gyorsabban, mint a kamionok, ha be akarják tartani a biztonságos követési távolságot. A csökkent sebességkülönbség és a kisebb szabad úttest-felület miatt már csak nagyon kevés lesz a sávváltásra és előzésre felhasználható rések száma, ennek megfelelően az előzések gyakorisága is drasztikusan csökken (4. ábra, jobb oldalt) és a személygépkocsik kénytelenek ugyanolyan lassan hajtani, mint a kamionok. Meg kell jegyeznünk, hogy ez az állapot (amelynek előfordulását a tapasztalatok is igazolják) nem is olyan előnytelen; a forgalom sűrűsége magas és stabil, a balesetveszély pedig csekély.

3. ábra. Egy autópálya x = 0 km-nél levő szűk keresztmetszetének szomszédságában kialakuló ötféle járműforgalmat modellező 5 diagram. Mind az 5 típusnak közös kialalakítója egy nagy visszafelé (x < 0) terjedő dugó. A közös “térkép" két független változója: (lásd az 1. ábránál) és Q_be Mindkettőnek dimenziója: jármű/km/sáv. a leszűkítés mértéke, Q_be az autópályán beérkező folyamatos járműforgalom erőssége.

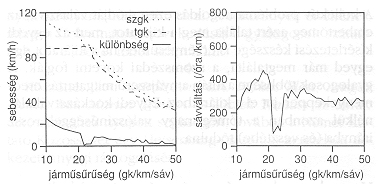
4. ábra. Baloldalt: A kétféle (szgk = személygépkocsi, illetve tgk = kamion) forgalom átlagos sebességének függése a járművek sűrűségétől. Egy keskeny sűrűség-intervallumban a kétféle jármű sebessége alig különbözik, amit a sávváltások számának (jobboldalt ábrázolt) radikális csökkenése az említett sűrűség-intervallumban megmagyaráz.

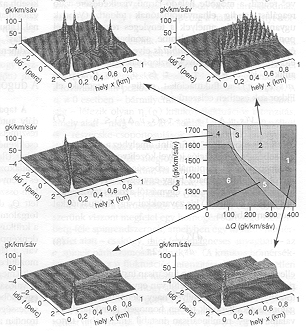
Érdemes még megvizsgálni, mi történik, ha egy sáv lezárása miatt útszűkület jön létre. ( http://www.theo2.physik.uni-stuttgart.de/treiber/MicroApplet/ , Szenario 3: Lane Closing alatti Java-Applet.) Amennyiben az autópályát csak kamionok használják, minden jármű ugyanazzal a kis sebességgel cammog tovább. Ha az összforgalom nem túl nagy, minden járműnek sikerül a szűkület előtt sávot cserélnie és a le nem zárt sáv igénybevételével az egész forgalom dugó képződése nélkül lebonyolítható. (5. ábra, baloldalt). Ha a (lassú) kamionok felét (gyors) személygépkocsikra cseréljük ki, változatlan összforgalom mellett azt várnók, hogy az átlagos járműsebesség megnövekszik. A valóságban azonban ennek pontosan az ellenkezője történik: a kétféle jármű vezetési stílusában várható (és valóban tapasztalt) különbség, különösképpen pedig az eltérő sebességek megzavarják a járművek áramlásának egyenletességét, és végül is megbénítják a forgalmat (5. ábra, jobboldalt). Ezt egyébként - enyhébb formában - zavaró szűkületek nélküli autópálya-szakaszokon is tapasztaljuk, amikor a forgalom intenzitása megközelíti a dinamikus kapacitásnak megfelelő értéket. Így érthető, hogy szakszerűen kiszámított és betartatott sebességkorlátozás - a járműsebességekben fellépő változásnak ezzel járó csökkenése miatt - megnöveli egy adott útszakasz áteresztő kapacitását.

5. ábra. Szűkület előtt megfigyelhető eltérő forgalomtípusok egyenlő forgalomkapacitások mellett. A baloldali kép szerint a forgalom “szabad", amikor minden jármű egyforma (kicsiny - a kamionokra jellemző) sebességgel halad. A jobboldali kép a forgalom leblokkolását mutatja, amely bekövetkezik, ha az szgk személygépkocsik és a tgk kamionok eltérő sebességgel haladnak.

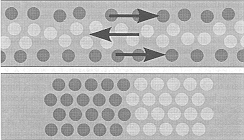
6. ábra. Fent: Folyosóban ellentétes irányba igyekvő gyalogosok forgalma sávossá szerveződik, ha a fluktuáció kismértékű. Lent: Nagyobb fluktuációk esetében a “freezing by heating" (fűtés okozta befagyás) figyelhető meg: kristályos blokkoló állapot alakul ki.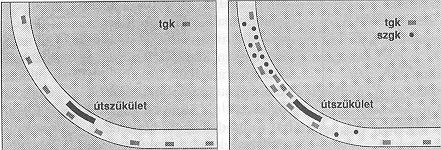

Gyalogosok forgalmának önszerveződése

További érdekes jelenségek figyelhetők meg kétdimenziós, kétirányú forgalomban, például folyosóban ellenkező irányba igyekvő gyalogosok részéről. Mivel gyalogosok felgyorsulási ideje 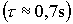nagyon kicsi, a továbbiakban a túlcsillapított esetnek megfelelő (4) egyenlettel számolunk; itt a 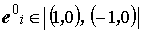célirány minden i gyalogosnál ugyanaz. Ezen kívül az egyszerűség kedvéért feltételezzük, hogy a cél-sebességek is azonosak (vagyis v⁰_i = v₀) és hogy a peremfeltételek periodikusak. A

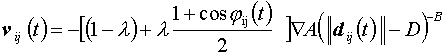  (9)

egyenlet (ahol és figyelembe veszi, hogy egy másik (j) gyalogossal való v_ji(t) kölcsönhatás annál gyengébb, minél kevésbé “van útban a j az i-nek", vagyis minél kevésbé látszik a j az i gyalogos e⁰_i célirányában levőnek. A, B és a D “gyalogosátmérő" pozitív állandók.

A számítások szerint közepes gyalogos-sűrűségek mellett gyorsan alakulnak ki az azonos irányban mozgók sávjai (6. ábra, fent). Az érdeklődő olvasó maga is lejátszhatja ezt a jelenséget ( http://www.theok.physik.uni-stuttgart.de/helbing/Pedestrians/corridor.html Java-Applet), de az utcán is megfigyelheti. A sávok kialakulása egyébként nem tételez fel olyan aszimmetriát, mint például azt, hogy a gyalogosok valamelyik oldalon szívesebben haladnak előre. Fontos viszont első sorban az, hogy az ellenkező irányba mozgó gyalogosok relatív sebessége nagyobb, emiatt ezeknek kitérő mozdulataira gyakrabban kerül sor mindaddig, amíg a sávok el nem különültek. Az így kialakult kollektív mozgásforma tehát minimalizálja a kitérő elmozdulások számát és maximalizálja az átlagos sebességeket a két választott irányban. Márpedig mindkét tény az egész rendszerre képzett átlagokban jut kifejezésre, noha modellünk még azt sem tételezi fel, hogy a gyalogosok legalább lokálisan optimalizálásra törekednek. Amint ki lehetett mutatni, ez azzal függ össze, hogy az ellentétes irányba törekvő gyalogosok között szimmetrikusak a kölcsönhatások. Ennél tovább is lehetett menni és kimutatni [15], hogy a meghajtott részecskék nagy rendszereinek több osztálya olyan, hogy amennyiben egyáltalán önszervező, úgy egyben optimalizálni is próbálja az állapotát. Ilyet már a személygépkocsik és a kamionok összefüggő tömbként való haladásában vehettünk észre, amikor is a sávváltások száma ezzel minimalizálódott [14].

Pánikba esett gyalogosok

Érdekes megfigyelni, mi történik, ha gyalogosok egyre idegesebben viselkednek, vagyis a fluktuációk intenzitása észrevehetően nő (a “hőmérséklet" emelkedik). Ilyen körülmények között nem tudnak sávok kialakulni (a “cseppfolyós állapot" nem marad fent). Meglepő módon az új halmazállapot nem “gáznemű", hanem nagyobb (!) összenergiájú “szilárd", “megfagyott" állapot (6. ábrán alul). Önhajtott sokrészecske-rendszereknél fellépő szokatlan jelenséget “freezing by heating"-nek nevezzük [16]. Lehetséges, hogy ez a magyarázata a pánikhelyzetekben gyakran tapasztalt, végzetes blokkolt állapotoknak.

Kézenfekvő kérdés, hogy mi lenne a legjobb stratégia, amivel tűzvész esetén a füst miatt láthatatlan kijáratok felé igyekezve, a tájékozódás lehetőségétől megfosztott embertömegnek sikerülhetne elhagynia a helyiséget. Kiderült, hogy a legjobb megoldás egyaránt tételezi fel az egyedi döntéshozatalt és a nyájszerű viselkedést. Modellező vizsgálataink szerint [17] célszerű, ha a gyalogosok az (5) egyenlet szerinti módon szomszédaikhoz igazodnak, de “némi" ()-szörös súlyozású sztochasztikus egyedi választás szerinti e^*_i irányítottsággal is mozognak:

  (10)

7. ábra. Baloldalt: Ellentétes irányba igyekvő gyalogosok szűk keresztmetszeten való áthaladásánál oszcillációk alakulnak ki. Jobboldalt: A szűk keresztmetszeten két irányban áthaladt részecskeszám különbségének időbeli alakulása nagyon hasonlít a Dow Jones index húszéves (némileg kisimított) alakulásához.

A kollektív problémamegoldás ezen módját választva, az embertömeg azért találja meg a kijáratot, mert az egyedi kísérletezési készsége is érvényesülhet: ha a kijáratot egy egyed már megtalálta, a szomszédai követni fogják. A gyalogosok többsége azután a nyájszerű magatartás eredményeképpen jut el a kijárathoz. Egyedi kockázatvállalás nélkül azonban a tömeg nagy valószínűséggel rossz irányba (és vesztébe) tódulna.

Van-e hasonlatosság a részvénypiacokkal?

Előrebocsátjuk, hogy a továbbiakban nem a pánikszerű viselkedést (a piac “összeomlását") tételezzük fel a részvénypiacon. Vizsgáljuk meg a tőzsdefolyamatok mindennapi dinamikáját minimalizálási alapon. Mondhatjuk, versengés folyik optimista (az árfolyamok emelkedésében bízó) spekulánsok (“bikák") és pesszimista (az árfolyamok csökkenésével számoló) spekulánsok (“medvék") között. Előbbiek veszik a részvényeket, növelik a keresetet (ezzel felhajtják az árakat), utóbbiak eladják a részvényeket, növelik a kínálatot (ezzel nyomják az árakat). Az optimisták és pesszimisták tehát ellentétes irányban hatnak az árak alakulására és eközben “példát mutatva" mintegy magukkal is ragadják kollegáikat, vagyis velük azonos vásárlási, illetve eladási döntésekre “csábítják". Ugyanakkor azonban a tranzakciók volumenére vonatkozólag némi korlátozások is vannak érvényben, amelyeket peremfeltételekkel (például szűkületekkel) lehetne modellezni.

Fentiek alapján el tudnánk képzelni párhuzamok vonását gyalogosok tömegének viselkedésével, amikor is az optimisták és pesszimisták előbbi tranzakcióinak megfelelhetnének a gyalogosok ellentétes irányba való mozgásai, a részvények árfolyamváltozásainak pedig megfelelne az ellentétes irányban áthaladó gyalogosok számának különbsége.

Gyalogosok dinamikus viselkedése szűk keresztmetszeteknél

A gyalogosok áramaiban ténylegesen megfigyelhető oszcilláció (vagyis a váltakozó irányú, csoportos áthaladás szűk keresztmetszeteken) a 7. ábrán baloldalt látható. ( http://www.theo2.physik.uni-stuttgart.de/helbing/Pedestrians/Door.html. Java-Applet) A magyarázat hasonló, mint a gyalogos-sávok kialakulásáé: egyszerűbb egy gyalogosnak követni valamelyik társát (például az ajtón át), mint az árammal szemben haladni. Hogyha azonban valamely gyalogosnak “némi szerencsével" (fluktuáció!) sikerül a vele szemben érkező tömegben frissen képződött résen át a saját választott irányában továbbhaladnia, akkor vele együtt ez több-kevesebb társának is fog sikerülni. Az ilyen oszcillációk - főleg, ha a modell peremfeltételei nyitottak rendszertelenek, csakúgy, mint a részvények árfolyamainak változásai. A részvények értékének átlagos (folyamatos) növekedését a gyalogosok számának növelésével lehet szimulálni.

Köszönet illeti Czirók Andrást, Farkas Illést, Ansgar Hennecket, Martin Treilert és Vicsek Tamást az ábrák elkészítéséhez nyújtott segítségért, továbbá a Német Kutató Közösséget egy Heisenberg ösztöndíj keretében érkezett anyagi támogatásért.

Irodalom

1. D. HELBING, H.J. HERRMANN, M. SCHRECKENBERG, D.E. WOLF (eds.): Traffic and Granular Flow '99 - Social, Traffic, and Granular Dynamics, Springer, Berlin (2000); in print.
2. K.L. SCHICK, A.A. VERVEEN - Nature 251 (1974) 599
3. E.E. EHRICHS, H.M. JAEGER, G.S. KARCZMAR, J.B. KNIGHT, V.Y. KUPERMAN, S.R. NAGEL, -Science 267(1995) 1632
4. P.B. UMBANHOWAR, F. MELO, H.L. SWVINNEY - Nature 382 (1996) 793
5. F.SCHWEITZER, W EBELING, B. TILCH - Phys. Rev. Lett. 80 (1998) 5044
6. T. VICSEK, A. CZIRÓK, E. BEN JACOB, I. COHEN, O. SHOCHET - Phys. Rev. Lett. 75 (1995) 1226
   E.V. AIBANO - Phys. Rev. Lett. 77(1996) 2129
7. TONER AND Y. TU - Phys. Rev. Lett. 75 (1995) 4326
8. CZIRÓK, M. VICSEK, T. VICSEK - Physica A 264 (1999) 299
9. CZIRÓK, A.-L. BARABÁSI, T. VICSEK - Phys. Rev. Lett. 82(1999) 209
10. M. BANDO, K. HASEBE, A. NAKAYAMA, A. SHIBATA, Y. SUGIYAMA - Phys. Rev. E 51 (1995) 1035
11. B.S. KERNER, P. KONHÄUSER - Phys. Rev. E 50 (1994) 54;
    M. BANDO, K. HASEBE, K. NAKANISHI, A. NAKAYAMA, A. SHIBATA, Y. SUGIYAMA - J. Phys. I France 5 (1995) 1389
12. B.S. KERNER, H. REHBORN - Phys. Rev. E 53 (1996) R1297
    M. TREIBER, A. HENNECKE, D. HELBING. in Ref. (1).
13. D. HELBING, A. HENNECKE, M. TREIBER - Phys. Rev. Lett. 82 (1999) 4360
14. D. HELBING, B.A. HUBERMAN - Nature 396(1998) 738
15. D. HELBING, T. VICSEK - New Journal of Physics 1 (1999) 13 (see http://www.njp.org/)
16. D. HELBING, I. FARKAS, T. VICSEK - Phys. Rev. Lett. 84 (2000) 1240
17. D. HELBING, I. FARKAS, T. VICSEK - Nature, submitted (2000)

________________________

Előadás az Ortvay Kollokviumon: Fordította Haiman Ottó.