Fizikai Szemle honlap |
Tartalomjegyzék |
Fizikai Szemle 2000/10. 329.o.
Dirk Helbing, Farkas Illés és Vicsek Tamás
a Nature 2000. szeptember 28-i számában megjelent írása alapján
A kollektív emberi magatartás egyik legkataszrofálisabb megjelenési formája az a pánik okozta, tömeges, fejvesztett menekülés, mely gyakran halálos kimenetelű balesetekhez is vezet, minthogy a tömeg embereket nyom össze vagy tipor el. Ezt a viselkedést néha életveszélyes szituációk váltják ki, mint például egy tűzeset egy zsúfolt épületben. Máskor az ülőhelyekért siető emberek között alakul ki ez a pánikszerű rohanás, megint máskor pedig látszólag minden ok nélkül. Bár a mérnökök folyamatosan dolgoznak ki módszereket az efféle szerencsétlenségek mértékének csökkentésére, ahogy a tömeges események száma és mérete egyre nő, ezek gyakorisága is emelkedni látszik. A pánikviselkedéssel szisztematikusan foglalkozó tanulmányokat és az ehhez hasonló tömegmozgások előrejelzésére alkalmas kvantitatív elméleteket mégis ritkán látni. A következőkben a gyalogosviselkedés modelljén keresztül fogjuk vizsgálni a tömegben jelentkező pániknak és a koordinálatlan mozgás előidézte összezsúfolódásnak mechanizmusait (és előfeltételeit). Szimulációnk gyakorlati megoldásokat ajánl a tömeg veszélyes nyomásának megelőzésére. Sőt, mi több, optimális stratégiát találunk a füsttel telt termekből való menekülésre, amely stratégia az egyéni viselkedés és a kollektív “csordaösztön" keverékét veszi alapul.
A pánikot mint a kollektív magatartásnak a megfelelő források hiányában vagy azok fogytán kialakuló, sajátos formáját ezideig elsősorban szociálpszichológiai szempontból vizsgálták. A pánikba eső egyének jellemzően alkalmazkodni képtelen és könyörtelen tömegmagatartást tanúsítanak, mint amilyen az összetorlódás és életveszélyes túlzsúfolódás. A megfigyelt összetorlódás koordinálatlan mozgás (“inkoordináció") eredménye, és függ az elérni kívánt előny jellegétől.
A menekülési pánik karakterisztikus tulajdonságait a következőképpen összegezhetjük:
(1) az emberek jelentősen gyorsabban mozognak vagy próbálnak mozogni a normálisnál;
(2) lökdösődni kezdenek, így az emberek közti kölcsönhatások fizikai természetűvé válnak;
(3) egy útszűkületben való mozgás - különösen a keresztülhaladás - koordinálatlanná válik;
(4) a kijáratoknál ívképződés és elakadás figyelhető meg;
(5) torlódások alakulnak ki;
(6) az összezsúfolt tömegben a fizikai kölcsönhatások összeadódnak veszélyes nyomást okozva ezzel, ami elérheti a 4450 N m-1-t is, amely elég egy acélkorlát elgörbítéséhez vagy egy téglafal ledöntéséhez;
(7) a menekülést tovább lassítják az elesett vagy sérült személyek, akik akadályt képeznek;
(8) az emberek hajlandóságot mutatnak a tömegmagatartásra, azaz arra, hogy azt tegyék, amit a többiek;
(9) a pótkijáratok gyakran vagy elkerülik a menekülők figyelmét, vagy nincsenek megfelelően kihasználva.
Ezek a megfigyelések arra ösztökéltek bennünket, hogy a menekülési pánik társadalmi jelenségét az önjáró sokrészecskés rendszerek mintájára modellezzük. A gyalogos tömegek dinamikáját modellező számítógépes szimulációink egy általánosított erőmodellre épülnek, mely főként a pánik során megfigyelt nyomás fatális következményének leírására alkalmas. Olyan szociopszichológiai és fizikai hatások keverékét vezetjük be, melyek a tömegben mutatott viselkedést befolyásolják: N gyalogos minden mi tömegű i tagja adott ![]() kívánt sebességgel szeretne haladni, adott
kívánt sebességgel szeretne haladni, adott ![]() irányban, ezért igyekszik ennek megfelelően alakítani valódi vi sebességét bizonyos karakterisztikus
irányban, ezért igyekszik ennek megfelelően alakítani valódi vi sebességét bizonyos karakterisztikus ![]() idő alatt. Ezzel egyidejűleg sebességfüggő távot próbál tartani a többi j gyalogostól és az F falaktól. Ezt egyénenként fij és fiF “kölcsönhatási erők" segítségével modellezhetjük. Matematikai megfogalmazásban: a sebesség t idő alatti megváltozását ekkor a gyorsulási egyenlet adja meg
idő alatt. Ezzel egyidejűleg sebességfüggő távot próbál tartani a többi j gyalogostól és az F falaktól. Ezt egyénenként fij és fiF “kölcsönhatási erők" segítségével modellezhetjük. Matematikai megfogalmazásban: a sebesség t idő alatti megváltozását ekkor a gyorsulási egyenlet adja meg
![]() (1)
(1)
miközben az ri(t) elmozdulást a sebesség adja meg vi(t) = dri /dt.
Két gyalogos, i és j azon pszichológiai tendenciáját, hogy igyekeznek egymástól távol maradni, egy Aiexp[(rij dij)/Bi] nij taszító kölcsönhatási erővel írjuk le, ahol Ai és Bi konstans. dij = |ri - rj| jelöli a gyalogosok tömegközéppontjai közötti távolságot, nij = (nij1, nij2) = (ri - rj)/dij pedig a j-ből i-be mutató egységvektor. A gyalogosok akkor érnek egymáshoz, ha dij távolságuk kisebb, mint az ri és rj sugarak rij = (ri + rj) összege. Ez esetben bevezetünk további két erőt a szemcsés rendszerek kölcsönhatásainak mintájára, amelyek elengedhetetlenek a pánikoló tömegben mutatkozó sajátos jelenségek megértéséhez: egy k (rij- dij) nij “térfogati erőt", ami a testkompresszió ellen hat és egy ![]() “csúszási súrlódást", ami a relatív tangenciális mozgást akadályozza, ha az i gyalogos közel kerül j-hez. Itt
“csúszási súrlódást", ami a relatív tangenciális mozgást akadályozza, ha az i gyalogos közel kerül j-hez. Itt ![]() jelenti a tangenciális irányt
jelenti a tangenciális irányt ![]() pedig a tangenciális sebességkülönbséget, míg k és
pedig a tangenciális sebességkülönbséget, míg k és ![]() nagy konstansokat jelöl. Összegezve az
nagy konstansokat jelöl. Összegezve az
![]() (2)
(2)
egyenlethez jutunk, ahol a g(x) függvény zérus, ha a gyalogosok nem érnek egymáshoz (dij > rij), máskülönben egyenlő az x argumentummal.
Ezzel 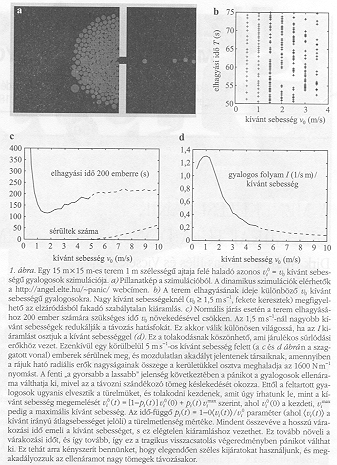 analóg módon kezeljük a falakkal történő kölcsönhatást, azaz ha diF jelenti az F faltól való távolságot, niF jelöli a rá merőleges irányt, és tiF a tangenciálist, akkor a megfelelő kölcsönhatási erőt a fallal a következő egyenlet adja meg
analóg módon kezeljük a falakkal történő kölcsönhatást, azaz ha diF jelenti az F faltól való távolságot, niF jelöli a rá merőleges irányt, és tiF a tangenciálist, akkor a megfelelő kölcsönhatási erőt a fallal a következő egyenlet adja meg
![]() (3)
(3)
Valószínűleg annak következtében, hogy a menekülési pánik váratlan és veszélyes esemény, ami kizárja az in vivo kísérletet, nem találtunk modellünk kvantitatív ellenőrzéséhez alkalmas adatokat. Ez az adathiány megköveteli a megbízható modellt. A paramétereket ezért a következőképpen határoztuk meg: m = 80 kg tömeggel reprezentálunk egy átlagos focirajongót. A ![]() kívánt sebesség meghaladhatja az 5 ms-1-ot (egész 10 ms-1-ig), de egy szoba elhagyásakor megfigyelt szabad sebességek nyugodt körülmények között
kívánt sebesség meghaladhatja az 5 ms-1-ot (egész 10 ms-1-ig), de egy szoba elhagyásakor megfigyelt szabad sebességek nyugodt körülmények között ![]() ~ 0,6 ms-1, normális helyzetben
~ 0,6 ms-1, normális helyzetben ![]() ~ 1 ms-1, ideges állapotban pedig
~ 1 ms-1, ideges állapotban pedig ![]() ~ 1,5 ms-1 szerint alakul. A gyorsulás idejére elfogadható becslés a
~ 1,5 ms-1 szerint alakul. A gyorsulás idejére elfogadható becslés a ![]() = 0,5 s. Ai = 2 x 103 N és Bi = 0,08 m mellett reprodukálhatjuk a normális kívánt sebességeknél tartott távolságot és illeszthetjük adatainkat a mért áramláshoz egy útszűkületben, ami annyi mint 0,73 személy másodpercenként egy 1 m nyílásszélességű ajtón
= 0,5 s. Ai = 2 x 103 N és Bi = 0,08 m mellett reprodukálhatjuk a normális kívánt sebességeknél tartott távolságot és illeszthetjük adatainkat a mért áramláshoz egy útszűkületben, ami annyi mint 0,73 személy másodpercenként egy 1 m nyílásszélességű ajtón ![]() ~ 0,8 ms-1 feltétel mellett. A k = 1,2 x 105 kgs-2 és a
~ 0,8 ms-1 feltétel mellett. A k = 1,2 x 105 kgs-2 és a ![]() = 2,4 x 105 kgm-1s-1 paraméter határozza meg az eltömődési effektust fizikai kölcsönhatások esetén. Bár a valóságban a legtöbb paraméter egyénről egyénre változik, minden gyalogosra azonos értékeket választottunk, hogy a kalibrálás és a hibatűrés érdekében minimalizáljuk a paraméterek számát, és hogy kizárjuk a paraméterek variációja miatt adódó természetellenes kiáramlást. Mindamellett ahhoz, hogy elkerüljük a modellből származó műtermékeket (a szimmetrikus konfigurációk pontosan kiegyensúlyozott erői miatti darabosságot), egy kis mértékű egyébként majdnem önkényes - egyenetlenségre van szükség. Ezt az egyenetlenséget a gyalogosok 2ri átmérőjének a [0,5 m; 0,7 m] intervallumon való egyenletes elosztásával vezettük be, ami közelítőleg a focirajongók vállszélességének eloszlása.
= 2,4 x 105 kgm-1s-1 paraméter határozza meg az eltömődési effektust fizikai kölcsönhatások esetén. Bár a valóságban a legtöbb paraméter egyénről egyénre változik, minden gyalogosra azonos értékeket választottunk, hogy a kalibrálás és a hibatűrés érdekében minimalizáljuk a paraméterek számát, és hogy kizárjuk a paraméterek variációja miatt adódó természetellenes kiáramlást. Mindamellett ahhoz, hogy elkerüljük a modellből származó műtermékeket (a szimmetrikus konfigurációk pontosan kiegyensúlyozott erői miatti darabosságot), egy kis mértékű egyébként majdnem önkényes - egyenetlenségre van szükség. Ezt az egyenetlenséget a gyalogosok 2ri átmérőjének a [0,5 m; 0,7 m] intervallumon való egyenletes elosztásával vezettük be, ami közelítőleg a focirajongók vállszélességének eloszlása.
A fenti 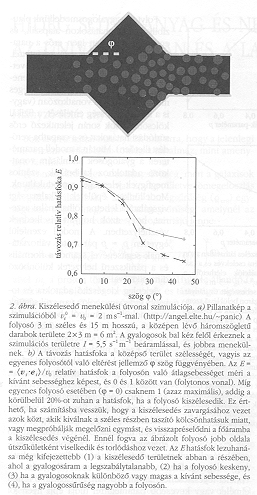 feltevésekkel élve a modellben most a menekülési pánik számos fontos jelenségét fogjuk szimulálni, melyek a paraméterek kis változásaira érzéketlenek, de szerencsére kevésbé kifejezettek lesznek széles kijáratoknál.
feltevésekkel élve a modellben most a menekülési pánik számos fontos jelenségét fogjuk szimulálni, melyek a paraméterek kis változásaira érzéketlenek, de szerencsére kevésbé kifejezettek lesznek széles kijáratoknál.
(1) Koordinálatlanság kialakulása elakadás miatt, A teremből való szimulált kiáramlás jól koordinált és szabályszerű, amennyiben a ![]() = v0 kívánt sebességek normálisak. Ám ha a kívánt sebesség 1,5 ms-1 felett van, azaz siető emberek esetében, a kijárat ívszerű eltorlaszolásának és az ív megtörésekor a termet elhagyó gyalogosok lavinaszerű csoportjainak irreguláris sorozatát tapasztaljuk
(1.a, b. ábra). Ez a jelenség összeegyeztethető a fent említett empirikus megfigyelésekkel, és a szemcsés áramlások tölcséren vagy öntőgaraton megfigyelhető szakaszos eltömődéseihez hasonlítható. (Mindenesetre megjegyezzük, hogy az efféle eltömődést a részecskék statikus súrlódásának tulajdoníthatjuk távoli kölcsönhatások feltételezése nélkül, illetve, hogy inkább az elég kicsi nyílások esetén figyeltek meg ilyen eltömődést, mint a hajtóerő variációjának okán.)
= v0 kívánt sebességek normálisak. Ám ha a kívánt sebesség 1,5 ms-1 felett van, azaz siető emberek esetében, a kijárat ívszerű eltorlaszolásának és az ív megtörésekor a termet elhagyó gyalogosok lavinaszerű csoportjainak irreguláris sorozatát tapasztaljuk
(1.a, b. ábra). Ez a jelenség összeegyeztethető a fent említett empirikus megfigyelésekkel, és a szemcsés áramlások tölcséren vagy öntőgaraton megfigyelhető szakaszos eltömődéseihez hasonlítható. (Mindenesetre megjegyezzük, hogy az efféle eltömődést a részecskék statikus súrlódásának tulajdoníthatjuk távoli kölcsönhatások feltételezése nélkül, illetve, hogy inkább az elég kicsi nyílások esetén figyeltek meg ilyen eltömődést, mint a hajtóerő variációjának okán.)
(2) A türelmetlenségből eredő “a gyors a lassabb jelenség". Mivel az eltömődéshez késlekedés társul, az, hogy az egyének gyorsabban igyekszenek mozogni (azaz emelni ![]() -t), lelassíthatja a terem elhagyásának átlagos sebességét, amennyiben a
-t), lelassíthatja a terem elhagyásának átlagos sebességét, amennyiben a ![]() súrlódási paraméter elég nagy
(1.c, d. ábra). Ez az effektus különösen tűz jelenlétében végzetes, miután a menekülő emberek a saját túlélési esélyeiket csökkentik. Az e miatti haláleseteket a tűz frontja által elért gyalogosok számával becsülhetjük
http://angel.elte.hu/~panic/.
súrlódási paraméter elég nagy
(1.c, d. ábra). Ez az effektus különösen tűz jelenlétében végzetes, miután a menekülő emberek a saját túlélési esélyeiket csökkentik. Az e miatti haláleseteket a tűz frontja által elért gyalogosok számával becsülhetjük
http://angel.elte.hu/~panic/.
Mivel a súrlódási tényezőnknek a tömegben átlagosan semmiféle fékező hatása nincsen, ha a falak elegendően messze vannak, az eltömődési effektus mélyén lévő ívképződés két effektust követel meg: egyrészt egy útszűkület - például egy ajtó - okozta lassulást, másrészt erős személyek közti súrlódást, mely akkor válik dominánssá, mikor a gyalogosok túlságosan közel kerülnek egymáshoz. Következésképp az eltömődés veszélye minimálisra csökkenthető az útszűkületek kerülésével a stadionok és más nyilvános épületek tervezésekor. Azt viszont meg kell jegyeznünk, hogy a torlódás a menekülési útvonalak kiszélesedésénél is bekövetkezhet. Ezt a meglepő eredményt illusztrálja a 2. ábra. A kiáramlást javíthatjuk a kijáratok előtt aszimmetrikusan elhelyezett oszlopok segítségével, amelyek a végzetes nyomás kialakulását is megakadályozzák ( http://angel.elte.hu/~panic/).
(3) Tömegmagatartás. Olyan szituációt fogunk vizsgálni, melyben a gyalogosok egy füsttel telített szobát próbálnak elhagyni, de ehhez előbb rá kell találniuk az egyik rejtett kijáratot
(3. ábra). Minden egyes i gyalogos választhat egyéni e; irányt vagy követheti adott Ri sugáron belüli j szomszédjainak átlagos ![]() irányát, vagy megpróbálkozhat e kettő keverékével. Feltesszük, hogy mindkét lehetőség szerepel valamilyen pi paraméterrel súlyozva
irányát, vagy megpróbálkozhat e kettő keverékével. Feltesszük, hogy mindkét lehetőség szerepel valamilyen pi paraméterrel súlyozva
![]() , (4)
, (4)
ahol Norm(z) = z / |z| a z vektor egységvektorát jelenti. Ebből következik, hogy egyéni cselekvést kapunk, ha pi kicsi, de csordamagatartást, ha pi nagy. Ezért pi az i egyén pánikállapotának mértékét tükrözi.
Modellünk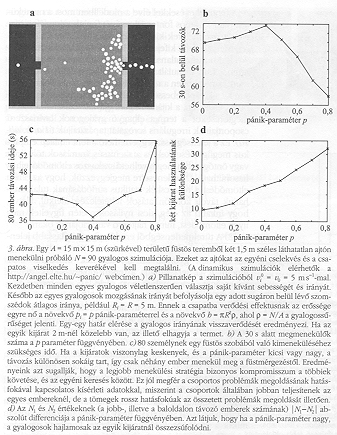 azt sugallja, hogy sem az egyéni cselekvés, sem a csordamagatartás nem hatékony
(3.b ábra). A tisztán egyéni viselkedés azt jelenti, hogy mindenki csak véletlenszerűen talál kijáratot, míg a tisztán csordamagatartás oda vezet, hogy végül is az egész tömeg ugyanabban a valószínűleg elzáródott - irányban halad, így aztán nem használják ki hatékonyan a rendelkezésre álló kijáratokat
(3.d ábra), ami egyezik a megfigyelésekkel. Ahogy azt
a 3.b és 3.c ábra mutatja, az optimális túlélési esélyt az egyéni és a csordamagatartás olyan keverékénél várjuk, ahol az individualizmus lehetővé teszi, hogy néhányan rátaláljanak a kijáratokra, a csapatba verődés pedig garantálja, hogy a többiek kövessék a sikeres megoldást. Ha a gyalogosok követik a falakat, ahelyett, hogy “visszaverődnének" róluk, azt várhatjuk, hogy a tömeg követése szintén torlódást okoz, és megint csak az ajtók rossz kihasználását
(1. ábra), az ellenkező irányban haladó egyéni mozgásúak pedig egymást akadályozzák.
azt sugallja, hogy sem az egyéni cselekvés, sem a csordamagatartás nem hatékony
(3.b ábra). A tisztán egyéni viselkedés azt jelenti, hogy mindenki csak véletlenszerűen talál kijáratot, míg a tisztán csordamagatartás oda vezet, hogy végül is az egész tömeg ugyanabban a valószínűleg elzáródott - irányban halad, így aztán nem használják ki hatékonyan a rendelkezésre álló kijáratokat
(3.d ábra), ami egyezik a megfigyelésekkel. Ahogy azt
a 3.b és 3.c ábra mutatja, az optimális túlélési esélyt az egyéni és a csordamagatartás olyan keverékénél várjuk, ahol az individualizmus lehetővé teszi, hogy néhányan rátaláljanak a kijáratokra, a csapatba verődés pedig garantálja, hogy a többiek kövessék a sikeres megoldást. Ha a gyalogosok követik a falakat, ahelyett, hogy “visszaverődnének" róluk, azt várhatjuk, hogy a tömeg követése szintén torlódást okoz, és megint csak az ajtók rossz kihasználását
(1. ábra), az ellenkező irányban haladó egyéni mozgásúak pedig egymást akadályozzák.
Folytonos gyalogosmodellünk plauzibilis kölcsönhatásokon alapszik, és egyszerűsége miatt igen erős a paraméterek variációjára való tekintettel. Épp ezért alkalmas arra, hogy következtetéseket vonjuk le belőle a menekülési pánik mélyén rejlő, lehetséges mechanizmusokra vonatkozóan (vagyis a kívánt sebesség emelését, a fizikai kölcsönhatások során jelentkező erős súrlódási hatásokat és a csapatba verődést illetően). Miután a modell paramétereit a gyalogosok áramlására vonatkozó adatokhoz kalibráltuk, számos megfigyelt jelenséget reprodukáltunk. Modellünket épületek alkalmassági vizsgálatára lehetne fölhasználni aszerint, hogy azok hogyan viselkednek vészhelyzetben. A modell ezenfelül egyetlen pi = p paraméter változtatásának segítségével számol a normális és a pánikszerű helyzetek különböző dinamikájával is.
Jelenleg kiegészítő adatokra és további videóanyagokra van szükségünk a
 menekülési pánikról, hogy modellünket mennyiségileg ellenőrizhessük, és alternatív modellekkel vethessük össze. Ezek a modellek figyelembe vehetik például a személyek közti irány- és
menekülési pánikról, hogy modellünket mennyiségileg ellenőrizhessük, és alternatív modellekkel vethessük össze. Ezek a modellek figyelembe vehetik például a személyek közti irány- és
sebességfüggő kölcsönhatásokat, részletezhetik a paraméterek egyénenkénti variációját, tanulmányozhatják a fluktuáció hatását, figyelembe vehetik a földre hulló embereket, beépíthetik a szóbeli információcserét, összetettebb stratégiát, illetve bonyolultabb kölcsönhatásokat vihetnek végig (akár háromdimenziósakat), vagy megengedhetik a stratégiák közötti váltogatást. Az elmélet fejlesztésének három útja van. A magasabb rendű elmélet vagy kevesebb paraméterrel tudja épp ilyen jól reprodukálni a vizsgálati eredményeket, vagy azonos számú paraméter mellett magasabb fokú egyezést ér el az adatokkal, vagy további megfigyeléseket reprodukál majd.
_____________________
Dirk Helbing a