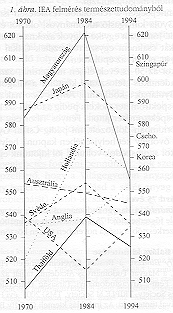
1. ábra IEA felmérés természettudományból
Fizikai Szemle honlap |
Tartalomjegyzék |
Fizikai Szemle 2001/1. 26.o.
A magyar tanulók fizikatudása egy nemzetközi vizsgálatban
Papp Katalin
Szegedi Tudományegyetem,
Kísérleti Fizikai Tanszék
Nemrégiben a fizikát szeretők, értők enyhén szólva felszisszentek, amikor a televízió egyik közkedvelt vetélkedő műsorában a tizenéves játékos, akinek feladata a munka mértékegységének négy alternatíva közül való kiválasztása volt, nem volt biztos tippjében, ezért kérte egyetemet végzett ismerősének segítségét. Az agrárvégzettségű szakember a "newtont" választotta, amit a játékos - talán a felnőttek iránti tekintélytisztelet miatt - el is fogadott.
Mennyire tükrözi ez a szégyenteljes esemény, amely az ünnepek miatt valószínű nagy nézőszám előtt zajlott, a társadalom fizikatudását? Vajon a szakembereken kívül hányan érezték a nézők közül, hogy ez az ismerethiány hasonló (vagy súlyosabb) kategóriájú, mint például Fortinbras nemzetiségének (norvég?, dán?) nem tudása? Valóban ennyire gyenge a magyar társadalom, a fiatalok fizikatudása?
Ez a kérdésfölvetés (is) adhatja az apropót: vizsgáljuk meg nemzetközi összehasonlításban, milyen a magyar tanulók természettudományos tudása, hogyan tudják az iskolai fizikatanítás során szerzett ismereteiket alkalmazni konkrét problémák megoldásánál. Ehhez jó lehetőséget kínál az IEA (International Association for the Evaluation of Educational Achievement) által szervezett tudásszintmérő vizsgálatok eredményeinek ismerete.
A természettudományos tudást mérő első felméréssorozat az IEA szervezésében az 1970-es évek elején volt (FISS: First International Science Study), majd megismétlődött a nyolcvanas években (SISS: Second International Science Study), lehetővé téve a változások megfigyelését is. A felmérést ismét elvégezték az 1994/95 tanévben, (TIMSS: Third International Mathematics and Science Study), ami a trendekkel és a következményekkel kapcsolatban felmerült további kérdések megválaszolását tette lehetővé.
Az IEA vizsgálatokban fiatalok százezreinek tudásszintjét mérik öt kontinens sok-sok országából, általában három korosztályban. Szakértők úgy tekintik az IEA felméréseit, mint legfontosabb és legrészletesebb adatanyagot a különböző országok oktatási rendszereinek teljesítmény-összehasonlításához. A felmérések volumenéből adódóan hatalmas adathalmaz áll rendelkezésre, a következtetéseket is tartalmazó kiadványok több kötetnyit tesznek ki [5, 6, 10].
Magyarország az IEA szervezésű vizsgálatokba - szerencsére - már korán bekapcsolódott, így mindhárom természettudományos felmérés magyar vonatkozásai is rendelkezésre állnak.
Az 1. ábrán a 14 éves korosztály (2. populáció) természettudományos teszten elért eredményességét mutatjuk be az említett három (1970, 1984, 1995) felmérés esetén. Ez az összehasonlítás (akár időben, akár országok közötti rangsorban) azért érdekes, mert ez a korcsoport érdemli talán a legnagyobb figyelmet, hiszen teljesítményük az alapoktatás eredményét tartalmazza. A legtöbb vizsgált országban 14 éves korban a teljes korcsoport jár iskolába, így a vizsgálat a teljes népesség természettudományos tudásáról ad információt.
Az adatok azt mutatják, hogy a magyar 14 évesek teljesítménye 1984-ben
volt a "csúcson", de a közelmúlt (1995) 5. helyezése sem szégyellnivaló az országok rangsorában. Az 1995-ös felmérésben szereplő magyar tanulók eredményeit a pedagógiai szaksajtóban többféle szempontból elemezték, értelmezték
[1, 7, 11]. A következőkben a fizikai ismereteket igénylő konkrét feladatokból válogatunk, azok eredményességével foglalkozunk a 14 és a 18 éves korosztályban.
TIMSS, 2. populáció (13-14 évesek),
fizika
A felmérés körülményeiről. A 2. populáció mintáját a 7. és 8. évfolyamra járó 14 éves tanulók alkották, összesen 45 országban, országonként 2000-6000 közötti elemszámmal!

1. ábra IEA felmérés természettudományból
A természettudományos teszt különböző tartalmú és szintű kérdéseket tartalmazott (összesen 135 item), a szakterületenkénti megoszlás a következő volt: földtudomány: 16%, biológia: 30%, fizika: 30%, kémia: 14%, környezetvédelem és természetismeret: 10%.
Az 1. táblázatban azon országok tanulóinak átlagos eredményeit tüntettük fel pontértékben, amelyek a reprezentativitás követelményének eleget tettek.
Az adatokból látható, hogy tanulóink mindkét évfolyamon a nemzetközi átlag fölött teljesítettek. A teljes adathalmaz mélyebb vizsgálata alapján megállapítható, hogy a magyar tanulók előtt 4 ország tanulói teljesítettek szignifikánsan jobban, 10 ország közel azonos teljesítményt mutatott és 26 ország tanulói érték el szignifikánsan rosszabb eredményt, mint a magyar nyolcadikosok [2].
A 2. táblázat tartalmi területenként mutatja be a tanulói teljesítményeket %-ban 8. osztályos tanulók esetén.
|
1. táblázat A 7. és 8. évfolyamra járó tanulók természettudományos teszten nyújtott teljesítménye |
||||
|
Ország |
8. évfolyam |
7. évfolyam |
||
|
Pontátlag |
Életkor |
Pontátlag |
Életkor |
|
|
Szingapúr |
607 (5,5) |
14,5 |
545 (6,6) |
13,3 |
|
Csehország |
574 (4,3) |
14,4 |
533 (3,3) |
13,4 |
|
Japán |
571 (1,6) |
14,4 |
531 (1,9) |
13,4 |
|
Korea |
565 (1,9) |
14,2 |
535 (2,1) |
13,2 |
|
Magyarország |
554 (2,8) |
14,3 |
518 (3,2) |
13,4 |
|
Anglia |
552 (3,3) |
14,0 |
512 (3,5) |
13,1 |
|
Belgium |
550 (4,2) |
14,1 |
529 (2,6) |
13,0 |
|
Szlovákia |
544 (3,2) |
14,3 |
510 (3,0) |
13,3 |
|
Oroszország |
538 (4,0) |
14,0 |
484 (4,2) |
13,0 |
|
Írország |
538 (4,5) |
14,4 |
495 (3,5) |
13,4 |
|
Svédország |
535 (3,0) |
13,9 |
488 (2,6) |
12,9 |
|
USA |
534 (4,7) |
14,2 |
508 (5,5) |
13,2 |
|
Kanada |
531 (2,5) |
14,1 |
499 (2,3) |
13,1 |
|
Norvégia |
527 (1,9) |
13,9 |
483 (2,9) |
12.9 |
|
Új-Zéland |
525 (4,4) |
14,0 |
481 (3,4) |
13,0 |
|
Hong-Kong |
522 (4,7) |
14,2 |
495 (5,5) |
13,2 |
|
Svájc |
522 (2,5) |
14,2 |
484 (2,5) |
13,1 |
|
Spanyolország |
517 (1,7) |
14,3 |
477 (2,1) |
13,2 |
|
Franciaország |
498 (2,5) |
14,3 |
451 (2,6) |
13,3 |
|
Izland |
494 (4,0) |
13,6 |
462 (2,8) |
12,6 |
|
Lettország |
485 (2,7) |
14,3 |
435 (2,7) |
13,3 |
|
Portugália |
480 (2,3) |
14,5 |
428 (2,1) |
13,4 |
|
Irán |
470 (2,4) |
14,6 |
436 (2,6) |
13,6 |
|
Ciprus |
463 (1,9) |
13,7 |
420 (1,8) |
12,8 |
|
Nemzetközi átlag |
516 |
479 |
||
Zárójelben az átlagértékekhez tartozó szórás nagyságát tüntettük fel.
|
2. táblázat Természettudományos eredményesség (%) tantárgyanként (8. osztály) |
||||||
|
Ország |
Teljes term. tud. teszt átlaga (135 item) |
Föld tudomány
(22 item) |
Élő tudomány
(40 item) |
Fizika
(40 item) |
Kémia
(19 item) |
Körny. véd. term. ism. (14 item) |
|
Szingapúr* |
70 (1,0) |
65 (1,1) |
72 (1,0) |
69 (0,8) |
69 (1,2) |
74 (1,1) |
|
Korea* |
66 (0,3) |
63 (0,5) |
70 (0,4) |
65 (0,5) |
63 (0,6) |
64 (0,8) |
|
Japán* |
65 (0,3) |
61 (0,4) |
71 (0,4) |
67 (0,3) |
61 (0,5) |
60 (0,7) |
|
Csehország |
64 (0,8) |
63 (1,2) |
69 (0,8) |
64 (0,7) |
60 (1,2) |
59 (1,1) |
|
Anglia* |
61 (0,6) |
59 (0,8) |
64 (0,8) |
62 (0,8) |
55 (0,8) |
65 (1,0) |
|
Magyarország |
61 (0,6) |
60 (0,8) |
65 (0,7) |
60 (0,6) |
60 (0,8) |
53 (0,8) |
|
Belgium (Fl) |
60 (1,1) |
62 (1,3) |
64 (1,2) |
61 (1,1) |
51 (1,3) |
58 (1,5) |
|
Szlovákia |
59 (0,6) |
60 (0,7) |
60 (0,6) |
61 (0,6) |
57 (0,8) |
53 (0,9) |
|
Svéd |
59 (0,6) |
62 (0,7) |
63 (0,7) |
57 (0,5) |
56 (0,7) |
52 (0,8) |
|
Kanada* |
59 (0,5) |
58 (0,6) |
62 (0,6) |
59 (0,4) |
52 (0,7) |
61 (0,7) |
|
Írország* |
58 (0,9) |
61 (1,1) |
60 (1,1) |
56 (0,8) |
54 (1,0) |
60 (1,1) |
|
USA* |
58 (1,0) |
58 (1,0) |
63 (1,1) |
56 (0,8) |
53 (1,2) |
61 (1,0) |
|
Oroszország |
58 (0,8) |
58 (0,8) |
62 (0,7) |
57 (0,9) |
57 (1,3) |
50 (0,8) |
|
Új-Zéland* |
58 (0,8) |
56 (0,9) |
60 (1,0) |
58 (0,7) |
53 (1,1) |
59 (1,2) |
|
Norvégia* |
58 (0,4) |
61 (0,6) |
61 (0,5) |
57 (0,4) |
49 (0,6) |
55 (0,8) |
|
Hong Kong* |
58 (1,0) |
54 (1,0) |
61 (0,9) |
58 (0,9) |
55 (1,0) |
55 (1,3) |
|
Svájc* |
56 (0,5) |
58 (0,6) |
59 (0,6) |
58 (0,5) |
50 (0,7) |
51 (0,8) |
|
Spanyolország* |
56 (0,4) |
57 (0,5) |
58 (0,5) |
55 (0,4) |
51 (0,7) |
53 (0,6) |
|
Franciaország |
54 (0,6) |
55 (0,8) |
56 (0,8) |
54 (0,5) |
47 (0,9) |
53 (0,9) |
|
Írország |
52 (0,9) |
50 (1,2) |
58 (1,0) |
53 (0,9) |
42 (0,8) |
49 (1,0) |
|
Lettország |
50 (0,6) |
48 (0,8) |
53 (0,7) |
51 (0,7) |
48 (0,8) |
47 (1,0) |
|
Portugália |
50 (0,6) |
50 (0,7) |
53 (0,6) |
48 (0,5) |
50 (0,9) |
45 (0,8) |
|
Litvánia |
49 (0,7) |
46 (0,9) |
52 (0,9) |
51 (0,7) |
48 (0,9) |
40 (1,0) |
|
Irán* |
47 (0,6) |
45 (0,6) |
49 (0,6) |
48 (0,7) |
52 (0,8) |
39 (1,1) |
|
Ciprus* |
47 (0,4) |
46 (0,6) |
49 (0,5) |
46 (0,4) |
45 (0,6) |
46 (0,8) |
|
Ausztria |
61 (0,7) |
62 (0,8) |
65 (0,7) |
62 (0,7) |
58 (1,1) |
55 (0,9) |
|
Németország |
58 (1,0) |
57 (1,0) |
63 (1,1) |
57 (1,0) |
54 (1,3) |
51 (1,3) |
|
Nemzetközi átlag |
56 (0,1) |
55 (0,1) |
59 (0,1) |
55 (0,1) |
51 (0,2) |
53 (0,2) |
Zárójelben az átlagértékekhez tartozó szórás nagyságát tüntettük fel.
* Integrált természettudományos oktatás, nincs tantárgyakra bontás.
Az adatokból látható, hogy a magyar tanulók tantárgyanként is a nemzetközi átlag fölött teljesítettek. A legjobb az eredmény kémiából és biológiából (4 ország végzett előttünk), földrajzból és fizikából 9, illetve 8 ország végzett előttünk, a környezeti és természetismereti kérdésekből viszont éppen
"hoztuk" az átlagot, előttünk 13 ország tanulói értek el jobb eredményt. A táblázatban
"*"-gal jelöltük meg azokat az országokat, amelyekben a 14 éves korosztályban integrált természettudományos tárgy (SCIENCE) keretében, nem külön tantárgyak formájában szerepelnek a természettudományos ismeretek. Érdemes ennek tudatában megvizsgálni az eredményeket. Megállapítható, hogy a táblázatban szereplő 27 ország közül az első 15 között Csehország, Magyarország, Belgium, Szlovákia, Svédország és Oroszország azok az országok, ahol a tanulók nem integrált tantárgyként tanulják a természettudományt.
Különbségek nemek és évfolyamok
között
Az adatok lehetővé teszik, hogy összehasonlítsuk a tanulók természettudományos teljesítményét nemektől függően. Általánosságban megállapítható, hogy a matematika eredményekkel ellentétben (ahol a magyar fiúk és a lányok azonos teljesítményt nyújtottak!) a természettudományos teszten a fiúk jobb eredményt értek el, mint a lányok, ez alól Thaiföld és Ciprus volt kivétel. A magyar tanulók esetében a 8. évfolyamos lányok 59%-os, a fiúk 63%-os teszteredményt értek el, a legkisebb a különbség biológiából (lányok 65%, fiúk 66%). Fizikából a nemzetközi trendhez hasonlóan a fiúk teljesítettek jobban, a legtöbb országban ez a különbség szignifikáns, így nálunk is: fiúknál 63%, lányoknál 56%-os az eredményesség. Érdemes megjegyezni, hogy legkisebb a két nem eredménye között a különbség a "Környezetvédelem és természetismeret" kérdéseknél, ahol sok helyütt a lányok voltak az eredményesebbek (nálunk: fiúk 55%, lányok 52%).
A hetedikeseknél hasonló tendenciákat tapasztalunk, csak kisebbek a különbségek a nemek között, a magyar tanulóknál az "összteszten" a fiúk eredménye 57%-os, a lányoké 54%. A legnagyobb a különbség a fizika tárgy esetén (fiúk 57%, lányok 51%), biológiából azonos a teljesítmény (fiúk, lányok 61%), viszont a Környezetvédelem-természetismeret kategóriában a lányok, ha kicsivel is (49%), de jobban teljesítettek (fiúk: 48%). A nemzetközi eredményeket figyelembe véve úgy tűnik, hogy a fiúk-lányok közötti különbség - a fiúk javára - az életkor előre haladtával növekszik.
Ha nemtől függetlenül vizsgáljuk a teljesítmények évolyam szerinti különbségét, akkor mint ahogy az várható, azt tapasztaljuk, hogy a magasabb évfolyamok tanulói jobban teljesítettek. A tudás gyarapodásának "mértéke" azonban már a különböző országok esetén igen különböző, Magyarország a 36-os különbséggel a középmezőnyben helyezkedik el, előttünk szerepel például Litvánia (73), Szingapúr (63), Anglia (40), utánunk pedig például az USA (26).
A magyar tanulók fizikából mutatott teljesítményét hat konkrét fizikafeladaton keresztül mutatjuk be, amely további tanulságok levonására ad lehetőséget.
1. feladat "Távolság-idő grafikon"
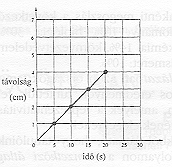
A grafikon egy hangya egyenes menti mozgását jellemzi. Ha feltételezzük, hogy sebessége állandó, milyen messzire jut a mozgás 30-ik másodpercében?
Válaszok: A) 5 cm, B)OK 6 cm, C) 20 cm, D) 30 cm
Ez a feladat egy egyszerű, ismeretalkalmazást igénylő, grafikon elemzéses feladat volt, amelyet a magyar tanulók 83%-os eredményességgel teljesítettek (8. osztály), ami a nemzetközi átlaggal éppen megegyezett. A hetedikes tanulók teljesítménye 81%-os, amely a nemzetközi átlag (79%) fölött volt. Ha az országok rangsorát tekintjük, akkor ezt a feladatot a hetedikeseknél 18 ország, a nyolcadikosoknál 28 ország tanulói oldották meg nálunk sikeresebben! Az egyenes vonalú egyenletes mozgás felismerése csak 3 ország esetén okozott igazán nehézséget (Irán, Kolumbia, Kuvait), amelyek 50% alatt teljesítettek, az országok 3/4 része az átlag fölött teljesített.
2. feladat "IZZÓ az áramkörben"
Az ábrákon egy elem és egy izzó kapcsolását mutatják be különböző anyagú rövidzár esetén. Melyik esetben világít az izzó? (rövidzárak: 1: levegő, 2: acélszeg, 3: rézpénz, 4: radírgumi)
Válaszok: A) 1 és 2, B)OK 2 és 3, C) 3 és 4, D) 1, 2 és 3, E) 2, 3 és 4.
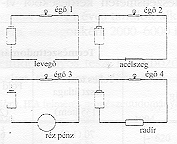
A zárt áramkör feltételének ismeretét, az anyagok vezetőképességét egyszerű alkalmazási szinten követelő feladatot a magyar tanulók 77% (7. osztály) és 85%-os (8. osztály) eredményességgel teljesítették. Ez a nemzetközi átlagot (69% 7. osztály, és 78% 8. osztály) jóval meghaladó teljesítmény az országok közötti rangsorban a 15., illetve a 12. helyezésre volt elegendő. Az életkorból adódó teljesítmény különbség viszonylag nagy volt ennél a feladatnál, amely az évfolyamok szerinti tananyag elrendezéssel magyarázható.
Megjegyezzük, hogy nem volt nehéz sikeres választ adni erre a feladatra az osztrák tanulóknak (91%-os teljesítmény), akiknek tankönyvében [4] a következő ábra szerepel:

3. feladat "Hang a térben"
A tengeren két hajó legénysége kiáltással kommunikál egymással. Miért nem lehetséges ugyanez két űrhajó legénysége esetén, ha a távolság a világűrben ugyanakkora?
Válaszlehetőségek:
Az ismeretek alkalmazását új szituációban igénylő feladat esetén a magyar tanulók átlag felett teljesítettek, hetedikeseknél 73% (nemzetközi átlag: 67%), nyolcadikosoknál 82% (nemzetközi átlag: 70%) volt az eredmény, előttünk 9 ország (7. osztály), illetve 3 ország (8. osztály) végzett. Ennél a feladatnál Korea (88%) és Japán (90%) teljesített kiemelkedően az országok között.
4. feladat "Az eső alma"
Az ábra egy földre eső almát mutat. A három jelölt helyzet közül melyikben hat a gravitáció az almára?
Válaszok: A) csak 2, B) 1 és 2, C) 1 és 3, D)OK 1, 2 és 3
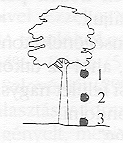
A gravitációs mező és a test kölcsönhatásának megértés-szintű ismeretét igénylő feladatot a tanulóknak körülbelül fele oldotta meg jól, a nemzetközi átlag 49% (7. osztály) és 55% (8. osztály). A kölcsönhatás szemléletet ismerő magyar tanulók teljesítménye átlag fölötti (69% és 72%), amivel a hetedikesek a harmadik, a nyolcadikosok a 2. helyezést értek el az országrangsorban. Mindkét évfolyamon Csehország tanulói értek el kimagasló eredményt. A megoldások tipikus hibája a B) lehetőség választása volt, amely azt a tévképzetet mutatja, hogy a Földön nyugalomban levő testre nem hat a gravitáció.
5. feladat "Hatásosabb gép"
Egy terület tisztítására A és B gépet használják. A táblázat mutatja, hogy milyen nagyságú területeket tisztítanak meg egy óra alatt és mennyi üzemanyagot fogyasztanak. Melyik gép alakítja át nagyobb hatásfokkal az üzemanyag energiáját munkává? Magyarázd meg válaszodat!
|
1 óra alatt megtisztított terület |
1 óra alatt fölhasznált üzemanyag |
|
|
A gép |
2 hektár |
3/4 liter |
|
B gép |
1 hektár |
1/2 liter |
Ennek a feladatnak a helyes megoldása gondot jelentett a tanulóknak.
Tipikusan az "ismeretalkalmazás új szituációban" kategóriájú, ahol két paraméter (terület, üzemanyag fogyasztás) hatását kellett figyelembe venni. (Tulajdonképpen arra kellett rájönni, hogy a 3/8 kisebb, mint az 1/2!) A 36%-os (8. évfolyam) és 29%-os (7. évfolyam) nemzetközi átlag úgy alakult ki, hogy csak kilenc ország volt a 27 között, ahol a tanulóknak legalább fele teljes választ adott. Magyarország eredménye a 8. évfolyamon éppen a nemzetközi átlag (36%), a hetedikeseknél 22%, ez jóval az átlag alatti. A feladatot Anglia nyolcadik évfolyamos tanulói oldották meg legjobban (51%), a magyar hetedikesek mellett még alacsony teljesítményt ért el Lettország, Litvánia és Spanyolország.
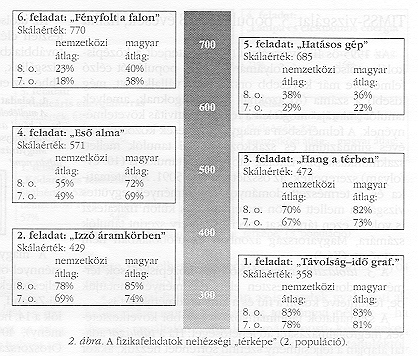
2. ábra A fizikafeladatok nehézségi "térképe" (2. populáció)
6. feladat "Fényfolt a falon"
Ha zseblámpával közelről világítunk falra, akkor kisebb fényfoltot kapunk, mintha távolról tennénk ugyanezt. Azt jelenti ez, hogy távolabbról világítva több fény jut a falra? Magyarázd meg válaszod!
Ismét egy "alkotó alkalmazás" típusú feladat, ahol a helyes megoldáshoz magas szintű gondolkodási műveletre (analízis, absztrakció) van szükség. Ez a feladat találtatott a legnehezebbnek, a tanulók kevesebb mint 1/4-e válaszolt helyesen, a nemzetközi átlag 18% (7. évfolyam) és 23% (8. évfolyam) volt. Örvendetes és meglepő, hogy a magyar tanulók ennél a feladatnál teljesítettek relatíve legjobban (38%, 40%), az országok közötti rangsorban, magasan a nemzetközi átlag fölött. A 7. évfolyamnál csak egy ország végzett előttünk (Irán), a nyolcadikosoknál pedig a 27 ország közül első helyen végeztünk.
A feladatokat, amelyek tükrözik a TIMSS fizikafeladatainak típusait és tartalmi területeit, a tanulói teljesítmények alapján egy "nehézségi skálán" helyezhetjük el.
Az így kialakított "nehézségi térkép" ( 2. ábra összesítve mutatja a nemzetközi és a magyar teljesítményeket. Az adatokból látható, hogy néhány feladatnál (1., 4., 6.) a magyar tanulóknál kicsi a különbség a hetedikes és nyolcadikos eredmények között, a 2. és s 5. feladatnál viszont igen nagy. Fontosabb megállapítás, hogy a magyar tanulók a magasabb szintű, értékesebb problémamegoldást igénylő feladatoknál jobban teljesítettek (3., 4., 6. feladat). Ez a következtetés, vagyis, hogy az ismereteket új helyzetben, köznapi problémák megoldására sikeresen alkalmazzák a magyar tanulók, nem cseng össze a 18 évesek nyújtotta teljesítménnyel, illetve a pedagógiai szakirodalomban ismertetett más hasonló felmérések eredményeivel
[3, 8]. A különbség okainak felderítése, a különbözőség magyarázata a konkrét feladatok összehasonlító elemzésével tanulságos lehet.
TIMSS-vizsgálat, 3. populáció, 18 évesek, fizika
Az 1995-ös IEA vizsgálat (TIMSS) kiterjedt a középiskolák utolsó éves évfolyamára is. A 3. populációt célzó felmérésre már kevesebb ország (21) vállalkozott, még kisebb a száma (8) azoknak az országoknak, amelyek tanulói "mintája" megfelelt a reprezentativitás követelményének: A felmérésben a magyar 18 évesek között utolsó éves gimnáziumi és szakközépiskolai tanulók mellett szakmunkásképző iskolák utolsó éves tanulói is (10. évfolyam) szerepeltek; az összlétszámuk: 5091. A matematika és a természettudományos teljesítmények együttes vizsgálata mellett külön matematika és külön fizikateszt is volt az ezen tárgyakat speciális tanterv szerint tanulók számára, Magyarország azonban ez utóbbiakban nem vett részt. (Kár!)
A 3. táblázatban az utolsó éves középiskolások természettudományos teszten elért eredményeit mutatjuk be, feltüntetve külön a fiú és a lány eredményeket is.
A számadatok tanulmányozása további következtetések megfogalmazására ad lehetőséget. Ha a táblázat adatai alapján a teljesítmény szerinti sorrendet nézzük, akkor a magyar tanulók (átlag: 471) az országok közötti sorrendben 18. helyen végeztek, eredményük a nemzetközi átlag (500) alatti, Litvánia, Ciprus és Dél-Afrika van csak utánunk. A fiúk és a lányok teljesítménye közötti változó különbségek (nemzetközi átlag: 39) azt mutatják, hogy minden felmért országban a fiúk teljesítettek jobban, a magyar tanulók ezen adata 29, amellyel a középmezőnyben helyezkednek el.
|
3. táblázat |
|||||
|
Utolsó éves középiskolások teljesítménye a természettudományos teszten |
|||||
|
Ország |
Pontátlag |
Fiú/lány arány |
Fiú |
Lány |
Különbség |
|
Svédország |
|
49/51 |
585 (5,9) |
534 (3,5) |
50 |
|
Új-Zéland |
|
49/51 |
543 (7,1) |
515 (5,2) |
28 |
|
Svájc |
|
56/44 |
540 (6,1) |
500 (7,8) |
40 |
|
Csehország |
• 487 (8,8) |
51/49 |
512 (8,8) |
460 (11,0) |
28 |
|
Oroszország |
|
38/62 |
510 (5,7) |
463 (6,7) |
47 |
|
Magyarország |
|
52/48 |
484 (4,2) |
455 (4,3) |
29 |
|
Litvánia |
|
36/65 |
481 (6,4) |
450 (7,3) |
31 |
|
Ciprus |
|
45/55 |
459 (5,8) |
439 (3,0) |
20 |
|
Ausztrália |
• 527 (9,8) |
42/58 |
547 (11,5) |
513 (9,4) |
34 |
|
Ausztria |
|
39/61 |
554 (8,4) |
501 (5,8) |
53 |
|
Kanada |
|
47/53 |
550 (3,6) |
518 (3,8) |
32 |
|
Franciaország |
• 487 (5,1) |
47/53 |
508 (6,7) |
468 (4,8) |
39 |
|
Izland |
|
48/52 |
572 (2,7) |
530 (2,1) |
41 |
|
Olaszország |
|
46/54 |
495 (6,7) |
458 (5,6) |
37 |
|
Norvégia |
|
51/49 |
574 (5,1) |
513 (4,5) |
61 |
|
USA |
|
50/50 |
492 (4,5) |
469 (3,9) |
23 |
|
Németország |
• 497 (5,1) |
56/44 |
514 (7,9) |
478 (8,5) |
35 |
|
Dánia |
• 509 (3,6) |
45/55 |
532 (5,4) |
490 (4,1) |
41 |
|
Hollandia |
|
52/48 |
582 (5,7) |
532 (6,2) |
49 |
|
Szlovénia |
• 517 (8,2) |
51/49 |
541 (12,7) |
494 (6,4) |
47 |
|
Dél-Afrika |
|
49/51 |
367 (11,5) |
433 (3,9) |
23 |
|
Nemzetközi átlag: |
500 |
|
521 |
482 |
39 |
Zárójelben az átlagértékekhez tartozó szórás nagyságát tüntettük
fel
 : az ország teljesítménye szignifikánsan magasabb a nemzetközi átlagnál.
: az ország teljesítménye szignifikánsan magasabb a nemzetközi átlagnál.
 : az ország teljesítménye szignifikánsan alacsonyabb a nemzetközi átlagnál
: az ország teljesítménye szignifikánsan alacsonyabb a nemzetközi átlagnál
• : nincs szignifikáns különbség az ország teljesítménye és a nemzetközi átlag között
Az utolsó éves középiskolások természettudományos teszten elért teljesítménye további elemzést igényel. A továbbiakban négy konkrét fizikafeladat kapcsán azt vizsgáljuk, hogyan járultak hozzá a fizikateljesítmények ehhez az eredményhez.
1. feladat "Kő és tenisziabda hatása"
A mellékelt ábrán két ablakot látunk. A baloldalit egy repülő kő törte be. A kővel azonos tömegű és sebességű teniszlabda ütközött a másik, azonos nagyságú és anyagi minőségű ablaknak, de az nem tört be.
Magyarázd meg, mi az oka, hogy a kő betörte az ablakot, a teniszlabda nem!
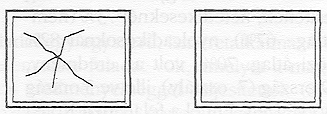
A magyar tanulók ezt a feladatot 54%-os teljesítménnyel oldották meg, az országok átlaga 57% volt. Jól teljesítettek (helyes válaszok aránya nagyobb, mint 70%) Új-Zéland, Svédország, Ausztrália tanulói, a magyar tanulók a 14. helyen végeztek (USA és Szlovénia azonos eredmény), 40% alatt teljesítettek között például Litvániát, Oroszországot és Ciprust találjuk.
A feladat az ütközés jelenségének konkrét gyakorlati alkalmazását követelte meg, ahol az ütközési idő-erő, a deformálhatóság, az ütközési felület nagyságának hatását kellett a két esetben végiggondolni.
2. feladat "Cipősarok a padlón"
Vannak magas sarkú cipők, amelyek a padlót koptatják. Az ilyen tűsarkú cipők sarok-átmérője 0,5 cm, míg a hagyományos cipők sarka körülbelül 3 cm átmérőjű. Magyarázzuk meg, hogy a magas sarkú cipő miért koptatja jobban a padlót!
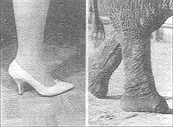
A feladatot sikeresen megoldó tanulók (a teljes választ adók %-a) az országok átlagában 41%, a magyar tanulók 47%-os eredményt értek el, előttünk nyolc ország végzett. Az első helyeken Hollandia (55%), Ausztrália (53%) és Németország (52%) található, nálunk jóval gyengébb eredményt ért el például Csehország (28%), USA (24%) és Szlovénia (20%).
A feladat megoldásához a nyomás, a nyomóerő, a nyomott felület fogalmait, kapcsolatát kellett alkalmazni mindennapos gyakorlati szituációban. A magyar teljesítmény a nemzetközi átlag fölötti ugyan, de a szükséges ismeretek egyszerűsége alapján jobb eredmény is elvárható lett volna. Talán, ha a magyar tankönyvekben szerepelt volna a következő ábra, akkor ezt a feladatot sikeresebben oldják meg (Ausztria tanulóinak eredménye ennél a feladatnál 51%).
3. feladat "Nukleáris energiaforrás"
Nukleáris energiát állíthatunk elő maghasadással és magfúzióval. A fúziót nem használják jelenleg energia forrásként a reaktorokban. Mi ennek az oka?
A helyes megoldások nemzetközi átlaga 40%, a magyar tanulók 41%-os eredményt értek el, tehát az átlag felett egy kicsivel. Ezzel az eredménnyel a 9. helyen végeztünk az USA tanulóival együtt, viszonylag jól szerepelt Svédország (54%), Dánia (51%), a sor végén találjuk Izlandot (28%), Szlovéniát (29%).
A felelet választásos formájú feladat magyarázatot, indoklást nem igényelt, mégis nehézséget okozott a tanulóknak. Felvetődhet a kérdés, hogy a gyenge teljesítményt vajon az iskolában szerzett tudás hiányának vagy az ismeretterjesztés (például TV) elégtelenségének tudhatjuk-e be?
4. feladat "Lámpa és az elektromos energia"
A lámpák üzemeltetésére elektromos energiát használunk. Választ kell adni, hogy a nyert fényenergia mennyisége több kevesebb, vagy ugyanakkora, mint a felhasznált elektromos energia? Indokold válaszod?
Ez az ismeretek gyakorlati alkalmazását igénylő, feleletválasztásos formájú feladat megoldása jelentette a középiskolások számára a legnagyobb nehézséget nemzetközi szinten (átlag: 21%) és a magyar tanulók számára (átlag: 16%) egyaránt. Helyes Választ a vizsgálatban részt Vett tanulók alig 1/5-e adott, az országrangsort vezető Szlovénia teljesítménye is csak 35%. Alacsony teljesítményt értek el például az USA tanulói (11%).
A lámpa melegedése, a mindennapi életben közvetlenül is tapasztalható hőveszteség "élménye" úgy tűnik hiányzik a tanulóknak, talán ez lehet a magyarázata az igen gyenge teljesítménynek.
A feladatok nehézségi fokát illusztráló 3. ábrán az összesített teljesítményeket is feltüntettük.
Nehéz a konklúzió megfogalmazása a magyar tanulók teljesítményéről a Vázolt négy feladat vonatkozásában. A gyenge eredmény lehetséges okai közül szerepeljen itt néhány:

3. ábra A fizikafeladatok nehézségi "térképe" (3. populáció)
A TIMSS vizsgálat ezen részében nemcsak a magyar 18 éves korosztály, hanem a többi ország tanulói is alacsony teljesítményt nyújtottak (lásd nemzetközi átlagok). Ez persze nem vigasztalhat bennünket, és az sem, hogy az alacsonyabb korosztály (2. populáció, 7., 8. évfolyam) - mint ahogy korábban láttuk -, magasabb teljesítményt mutatott.
A számszerű eredmények mélyebb analízise, például a helytelen tanulói válaszok elemzése, segítséget adhat a további okok kiderítéséhez és a teendők megfogalmazásához.
A teszten elért teljesítményt befolyásoló tényezők - tantárgyi vonzódás és a tanulói környezet
hatása
Természettudományos attitűd és a teljesítmény
A rendelkezésünkre álló adathalmaz lehetőséget ad arra, hogy megvizsgáljuk, a természettudományos tárgyakhoz való kötődés (attitűd) és a felmérés során elért teljesítmény milyen kapcsolatban van egymással. A kérdéskör tárgyalását és vázlatos bemutatását azért is fontosnak, a témához szorosan illeszkedőnek érezzük, mert saját hazai attitűdvizsgálataink [9] eredményeihez kapcsolódhatunk. A trendek, a kapcsolatok bemutatásához most nem a felmérés teljes adatállományát, hanem csak kiragadott országok jellemzőit használjuk fel, a TIMSS-ben alkalmazott tanulói és tanári kérdőívek adatai alapján.
|
4. táblázat |
|||||
|
14 éves tanulók véleménye a tantárgyak szeretetéről |
|||||
|
Ország |
A "szeretem" és a "nagyon szeretem" kategóriát választó tanulók aránya %-ban |
Teljesítmény (pontátlag) |
|||
|
Integrált term. tud. |
Biológia |
Földrajz |
Fizika |
||
|
Anglia |
78 |
- |
- |
- |
552 |
|
Ausztrália |
60 |
- |
- |
- |
527 |
|
Ausztria |
- |
70 |
55 |
49 |
520 |
|
Csehország |
- |
65 |
65 |
44 |
487 |
|
Irán |
93 |
- |
- |
- |
470 |
|
Japán |
56 |
- |
- |
- |
571 |
|
Korea |
59 |
- |
- |
- |
565 |
|
Magyarország |
- |
73 |
69 |
49 |
554 |
|
Portugália |
- |
90 |
- |
81 |
480 |
|
Szingapíu |
92 |
- |
- |
- |
607 |
|
Szlovákia |
- |
69 |
72 |
51 |
544 |
|
Svédország |
- |
61 |
66 |
63 |
535 |
|
USA |
71 |
- |
- |
- |
534 |
|
5. táblázat |
|||||
|
Végzős középiskolások véleménye a tantárgyak szeretetéről |
|||||
|
Ország |
A "szeretem" és a "nagyon szeretem" kategóriát választó tanulók aránya %-ban |
Teljesítmény (pontátlag) |
|||
|
Biológia |
Kémia |
Földrajz |
Fizika |
||
|
Ausztrália |
60 |
37 |
53 |
34 |
527 |
|
Ausztria |
72 |
38 |
61 |
36 |
520 |
|
Csehország |
60 |
29 |
66 |
26 |
487 |
|
Dél-Afrika |
67 |
49 |
68 |
47 |
349 |
|
Izland |
86 |
59 |
65 |
51 |
549 |
|
Kanada |
70 |
50 |
71 |
44 |
532 |
|
Magyarország |
63 |
24 |
61 |
28 |
471 |
|
Szlovénia |
54 |
29 |
69 |
35 |
517 |
|
Svájc |
65 |
46 |
71 |
44 |
523 |
|
Svédország |
69 |
46 |
72 |
47 |
559 |
|
Új-Zéland |
63 |
38 |
55 |
35 |
529 |
|
USA |
67 |
49 |
68 |
47 |
480 |
Mennyire szeretik a tanulók a természettudományos tárgyakat?
A fenti kérdésre adott tanulói válaszok (a "nem szeretem"-től a "nagyon szeretem"-ig terjedtek) közül a szeretem, és nagyon szeretem alternatívát választók %-os arányát tüntettük fel a 4. táblázatban.
Megállapíthatjuk, hogy az integrált természettudomány (science) formájában tanult természettudományi. ismeretek esetén pozitívabb kötődés alakul ki (táblázat 1. oszlopa) a tanulókban. A szeparált tantárgyi formában tanító országoknál a legkedvezőbb a biológia tantárgy megítélése (60% fölötti), és igen kedvezőtlen a fizikatárgyról alkotott vélemény (Csehország, Ausztria, Magyarország):
Szoros korrelációt a tantárgyi hozzáállás és a teszten nyújtott teljesítmény között nem tapasztalunk, a "pozitív kötődés - jó teljesítmény"-re épp úgy találhatunk példát (Szingapúr), mint a "nagyon szeretem", de kevésbé eredményes teljesítményre (például Irán, Portugália). Ha részletesebben megvizsgáljuk az attitűd háttérváltozó hatását attól függően, hogy fiúk vagy lányok nyilatkoztak, akkor az adatok részletes ismertetése nélkül megállapítható, hogy a fiúk általában kedvezőbb hozzáállásúak, a legnagyobb, szignifikáns különbség a fiúk javára fizikatárgy megítélésénél tapasztalható, ezen belül is a szlovák, a holland és a német leánytanulók szeretik legkevésbé a fizikatárgyat:
Az adatok tanulmányozása során szembeötlik, hogy az egyes tantárgyak "tetszési indexe" milyen széles intervallumon belül változik, a legszélsőségesebb megítélés a fizikatárgynál tapasztalható (Csehország 44%, Portugália 81%).
Hasonló eredményt mutat ugyanezen háttérváltozó hatása a teljesítményre a 3. populáció esetén, az adatokat az 5. táblázat tartalmazza.
A tantárgyak kedveltségi sorrendje teljesen megegyezik ugyanezen korosztály számára szervezett saját empirikus vizsgálatunk eredményével [9], nevezetesen a biológia tantárgy a legkedveltebb a természettudományos tárgyak közül, a kémia és a fizika lényegesen kisebb "népszerűségnek örvend". A legalacsonyabb érték fizikából a cseh tanulók véleménye alapján adódott (csak 26%-uk nyilatkozott úgy, hogy szereti, illetve nagyon szereti a fizikát), az "“abzolút" negatív kötődést a magyar tanulók kémia megítélése szolgáltatta (24%). A fiú-lány vélemények összehasonlítása ugyancsak megerősíti hazai vizsgálatunkat: a biológiát a lányok jobban szeretik, a kémiát, fizikát a fiúk szeretik jobban, a legkedvezőtlenebb hozzáállása a cseh, a magyar, az ausztrál és az új-zélandi leány tanulóknak van fizikatantárgyból.
|
6. táblázat |
||||
|
Számítógépes környezet - természettudományi teszten nyújtott teljesítmény, 8. évfolyam |
||||
|
Ország |
Van-e számítógép otthon? |
|||
|
Igen |
Nem |
|||
|
Tanulói arány % |
Pontátlag |
Tanulói arány % |
Pontátlag |
|
|
Anglia |
89 |
553 |
11 |
558 |
|
Portugália |
73 |
554 |
27 |
525 |
|
Ausztria |
59 |
565 |
41 |
548 |
|
Csehország |
36 |
593 |
64 |
563 |
|
Irán |
4 |
474 |
96 |
472 |
|
Korea |
39 |
584 |
61 |
553 |
|
Lettország |
13 |
487 |
87 |
485 |
|
Magyarország |
37 |
581 |
63 |
539 |
|
Oroszország |
35 |
542 |
65 |
536 |
|
Románia |
19 |
504 |
81 |
482 |
|
Szingapúr |
49 |
626 |
51 |
590 |
|
Szlovákia |
31 |
561 |
69 |
537 |
|
USA |
59 |
555 |
41 |
506 |
|
7. táblázat |
|||||||
|
A számítógép iskolai alkalmazásának gyakorisága és a természettudományos és matematika teszten elért teljesítmény, 18 évesek |
|||||||
|
Ország |
Számítógép-használat az iskolában |
Összes tanuló teljesítménye (pontátlag) |
|||||
|
Nagyon ritkán, soha |
Hetente |
Naponta |
|||||
|
Tanulói arány % |
Pontátlag |
Tanulói arány % |
Pontátlag |
Tanulói arány % |
pontátlag |
||
|
Ausztrália |
25 |
498 |
28 |
534 |
34 |
544 |
527 |
|
Ausztria |
34 |
496 |
39 |
529 |
20 |
546 |
520 |
|
Csehország |
62 |
450 |
20 |
524 |
9 |
552 |
487 |
|
Dánia |
18 |
501 |
41 |
529 |
27 |
549 |
509 |
|
Kanada |
21 |
500 |
34 |
535 |
28 |
544 |
532 |
|
Litvánia |
69 |
460 |
19 |
481 |
4 |
482 |
461 |
|
Magyarország |
65 |
471 |
19 |
500 |
12 |
525 |
471 |
|
Oroszország |
47 |
468 |
32 |
483 |
12 |
504 |
481 |
|
Szlovénia |
38 |
492 |
26 |
531 |
21 |
546 |
517 |
|
Svájc |
38 |
501 |
24 |
549 |
28 |
550 |
523 |
|
Svédország |
32 |
518 |
31 |
566 |
19 |
614 |
559 |
|
USA |
27 |
435 |
27 |
485 |
31 |
494 |
480 |
Terjedelmi okok miatt nem közöljük azon tanulócsoport eredményeit, akik nyilatkozatuk szerint havonta találkoznak számítógéppel az
iskolában.
Tanulói környezet és a természettudományos teljesítmény
A TIMSS vizsgálat során a tudásmérés mellett az IEA hagyományainak megfelelően információt kapunk további háttérváltozókról, amelyeket tanulói, tanári, iskolairányítói kérdőívek segítségével gyűjtöttek össze. Többek között a számítógépes környezet, az osztály mérete, a tanár életkora, tapasztalata, a tanári és tanulói kísérletek gyakorisága a tanulók iskolán kívüli tevékenysége témákban juthatunk értékes információkhoz. Ezekből az adathalmazokból a számítógép alkalmazását és a tanulók televízió-nézési szokásait emeljük ki.
|
8. táblázat |
|||||||
|
Televíziózási, videózási szokások és a teljesítmény, 14 évesek |
|||||||
|
Ország |
Napi televízió-, videonézési idő |
Összes tanuló teljesítménye (pontátlag) |
|||||
|
Kevesebb mint egy óra |
3-5 óra |
Több mint 5 óra |
|||||
|
Tanulói arány % |
Pontátlag |
Tanulói arány % |
Pontátlag |
Tanulói arány % |
Pontátlag |
||
|
Anglia |
20 |
545 |
31 |
558 |
11 |
530 |
552 |
|
Ausztrália |
24 |
556 |
27 |
541 |
9 |
502 |
545 |
|
Ausztria |
25 |
562 |
17 |
558 |
5 |
522 |
558 |
|
Csehország |
15 |
578 |
31 |
571 |
9 |
546 |
574 |
|
Izrael |
9 |
507 |
44 |
532 |
14 |
513 |
524 |
|
Japán |
9 |
579 |
30 |
564 |
9 |
547 |
571 |
|
Korea |
32 |
574 |
20 |
555 |
7 |
534 |
565 |
|
Litvánia |
12 |
469 |
32 |
476 |
12 |
467 |
476 |
|
Magyarország |
11 |
569 |
33 |
552 |
15 |
522 |
554 |
|
Oroszország |
12 |
526 |
32 |
544 |
14 |
538 |
538 |
|
Szingapúr |
7 |
633 |
37 |
597 |
6 |
582 |
607 |
|
Svájc |
45 |
534 |
9 |
502 |
2 |
- |
522 |
|
USA |
22 |
542 |
25 |
533 |
13 |
493 |
534 |
Terjedelmi okok miatt a táblázatokban nem tüntettük föl azon tanulócsoport eredményeit, akik nyilatkozatuk szerint 1-2 órát nézik naponta a
televíziót.
Változatos képet mutat a tanulók otthoni számítógép ellátottsága (6. táblázat), ez alapján az országok akár be is sorolhatók gazdag (például Anglia), kevésbé gazdag (például Magyarország), szegény (például Románia) csoportokba. Azok a tanulók, akik számítógéppel rendelkeznek otthon, a természettudományos teszten lényegesen jobb eredményt értek el (például Magyarország, Szingapúr, Korea és USA).
A számítógép iskolai alkalmazásának gyakorisága (7. táblázat) és a természettudományos teszten nyújtott teljesítmény között szignifikáns kapcsolatot találunk, amely legmarkánsabbnak Magyarország, Csehország, Szlovénia és USA esetén mutatkozik.
Különösen tanulságos annak tanulmányozása, hogy i széles határok között változik például
a "nagyon soha" kategóriát választó tanulók aránya az országok között (például Dánia 18%, Magyarország 65%), illetve milyen, a nemzeti átlagot jóval meghaladó teljesítményt értek el azok a tanulók, akik nyilatkozatuk szerint naponta találkoznak számítógép-alkalmazással az iskolában (például Magyarország, Csehország, Svédország).
Televízió-nézés, és a természettudományos teszten nyújtott
teljesítmény
Természettudományos tudás és a TV előtt eltöltött idő kapcsolata, összehasonlítása nem kézenfekvő, kétkedésre, vitára ösztönözheti a szakembereket, laikusokat egyaránt. Hogy zárásként mégis ezt a kapcsolatot mutatjuk be mindkét korosztálynál (8., 9. táblázat), annak az oka az, hogy ez az a háttérváltozó (TV előtt eltöltött idő), amely érték alapján Magyarország vezeti az országok közötti rangsort. Úgy gondoljuk, ezt a “dicsőséget" szívesen átengednénk más országoknak, talán az igazi gondot ez okozza.
A sok adatból jól látszik, hogy a TV előtt eltöltött idő növekedése kedvezőtlenül befolyásolja a teszten nyújtott teljesítményt. A magyar 14 évesek 15%-a nyilatkozott úgy, hogy naponta több mint 5 órát nézi a televíziót (videót), ez igen magas arány, ugyanez a szám például Svájc esetén 2%, Ausztria esetén 5%. A 8. és 9. táblázat utolsó oszlopában a feltüntetett nemzeti átlagok segítenek a különböző tanulócsoportok teljesítményeinek összehasonlításában.
Végezetül annak illusztrálására, hogy a bemutatott statisztikákból levont általánosítások mennyire helytállóak és időtállóak, a legfrissebb 1999-es IEA-szervezésű természettudományos vizsgálat 14 évesekre vonatkozó felméréséből a következőket emeljük ki ( http://timss.bc.edu): Magyarország 38 ország közül az előkelő 3. helyen szerepel az országok rangsorában a természettudományos teszten elért eredmény alapján. Tantárgyanként a magyar tanulók földrajzból az 1., biológiából 6., fizikából 5., kémiából 2. helyet érték el, mindenütt magasan a nemzetközi átlag fölött teljesítettek. Vészharang, Vagy örömmámor? A tudásszint mérés eredményeinek globális megítélése óvatosságra int, a lényeg a részletekben, a számszerű eredmények mögött van.
|
9. táblázat |
|||||||
|
Televíziózási, videózási szokások és a teljesítmény, 18 évesek |
|||||||
|
Ország |
Napi televízió-, videonézési idő |
Összes tanuló teljesít-ménye (pontátlag) |
|||||
|
Kevesebb mint egy óra |
3-5 óra |
Több mint 5 óra |
|||||
|
Tanulói arány % |
Pontátlag |
Tanulói arány % |
Pontátlag |
Tanulói arány % |
Pontátlag |
||
|
Ausztrália |
34 |
532 |
17 |
527 |
5 |
476 |
527 |
|
Ausztria |
37 |
532 |
14 |
507 |
2 |
- |
520 |
|
Csehország |
21 |
512 |
22 |
450 |
5 |
429 |
487 |
|
Dánia |
32 |
541 |
15 |
519 |
2 |
- |
509 |
|
Kanada |
38 |
531 |
15 |
512 |
3 |
502 |
532 |
|
Litvánia |
21 |
473 |
24 |
459 |
6 |
439 |
461 |
|
Magyarország |
31 |
505 |
19 |
451 |
6 |
426 |
471 |
|
Oroszország |
15 |
490 |
31 |
469 |
7 |
451 |
481 |
|
Szlovénia |
44 |
520 |
10 |
486 |
3 |
484 |
517 |
|
Svájc |
55 |
545 |
8 |
505 |
2 |
- |
523 |
|
Svédország |
33 |
576 |
15 |
526 |
1 |
- |
559 |
|
Új-Zéland |
28 |
537 |
20 |
511 |
7 |
506 |
529 |
|
USA |
40 |
483 |
15 |
458 |
5 |
424 |
480 |
Terjedelmi okok miatt a táblázatban nem tüntettük föl azon tanulócsoport eredményeit, akik nyilatkozatuk szerint 1-2 órát nézik naponta a
televíziót. Irodalom