Barabási Albert-László:
A WEB FIZIKÁJA

	Térkép 100000 Internet routerről és fizikai kapcsolataikról. Ezt a térképet számtalan adatcsomag követésével kaptuk, miközben egyik gépről a többire küldtük. Felfedi, hogy a pár erősen csatolt csomópont tartja egybe a hálózatot.
A szociológusok eszközöket kölcsönöznek a hálózatkutatóktól, hogy jobban bemutathassák az emberek csoportjainak viszonyát egymással. Az ábra egy szociális hálózatot mutat be Canberrából (Ausztrália).

1. ábra. (a) Az Erdős-Rényi véletlen-gráf modell N pontból áll, melyek mindegyike p valószínűséggel kapcsolódik a másikhoz. Erre a hálózatra N = 10 és p = 0,2. Ha 45 párt tudunk alkotni, akkor körülbelül 9 kapcsolatot várunk. (b) A skálafüggetlen-modell feltételezi, hogy a hálózat folyamatosan nő új pontok hozzáadásával. Az új pont (piros) hozzákapcsolódik két meglevő ponthoz (fekete) a t+1. időpontban. Az új csomópont nagyobb valószínűséggel kapcsolódik erősen kapcsolt csomóponthoz a preferenciális kapcsolódás elve szerint. (c) A hálózat kapcsoltsága a P(k) valószínűséggel írható le, ahol a csomópontnak k kapcsolata van. Véletlen-gráfok esetében a P(k)-nak erős maximuma van (k)-nál és exponenciálisan cseng le nagy k esetén. (d) Skálafüggetlen-modellben nincs P(k)-nak csúcsa, és hatványfüggvény szerint cseng le, P(k) ~ K- nagy k esetén. (e) A véletlen-gráf igen homogén, vagyis a legtöbb csomópontnak azonos a fokszáma. (f) A legtöbb csomópontnak a skálafüggetlen-modellben egy vagy két kapcsolata van, míg egy néhánynak viszont igen sok kapcsolata van, ez garantálja, hogy a rendszer teljesen kapcsolt. A csomópontok több mint 60%-a elérhető az erősen kapcsolt pontokból, míg ez csak 27% a véletlen hálózatok esetében. Ez azt bizonyítja, hogy a hubok esetében a skálafüggetlen-modell a kulcstényező. Mindkét hálózat 130 csomópontot és 430 kapcsolatot tartalmaz.

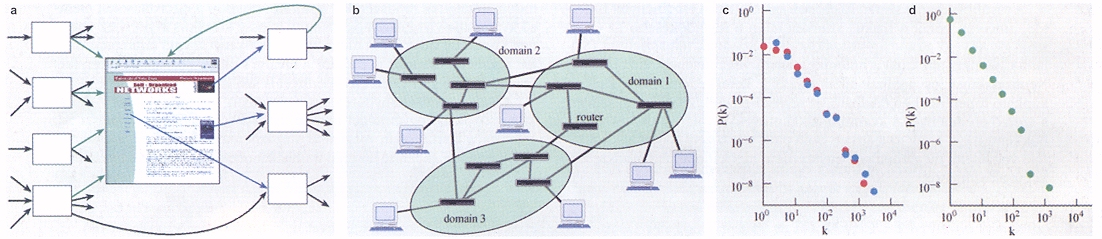
2. ábra. (a) A World Wide Web esetében a Web dokumentumok a csomópontok és mindegyikük az úgynevezett URL-lel van egyértelműen azonosítva. A legtöbb dokumentum, így a mi website-unk is, a www.nd.edu/~networks, is tartalmaz URL-t, melyek egy másik weboldalra mutatnak. Ezek az URL-ek kimenő linkek kki, három közülük az ábrán is látható kék nyíllal jelölve. Jelenleg 80 dokumentum mutat világszerte a lapunkra, kbe, bejövő zöld nyíllal jelölve. Miközben csak rajtunk múlik a kimenő linkek száma, a bejövő linkek számát más emberek választják meg, ami meghatározza a weboldal népszerűségét. (b) Az Internet másrészt a routerek hálózata, melyek adatcsomagokat navigálnak egyik számítógépről a másikra. A routerek egymás között is össze vannak kötve számos fizikai és drótnélküli kapcsolattal és domain csoportokba vannak szervezve. (c) A valószínűségi eloszlás, hogy egy weboldal kbe (zöld) és kki (kék) kapcsolattal rendelkezik hatványfüggvényt követ; Ez az eredmény Hawoong Jeong által 325 000 weboldal összegyűjtött adatán alapul. (d) Az eloszlás foka router-szinten, ahol k a router más routerekkel levő kapcsolatainak számát jelöli. Ez a kutatás Ramesh Govindan (University of Southern California) 260000 routeren végzett vizsgálatán alapul és bemutatja, hogy az Internet hatványfüggvény jellegű viselkedést mutat.

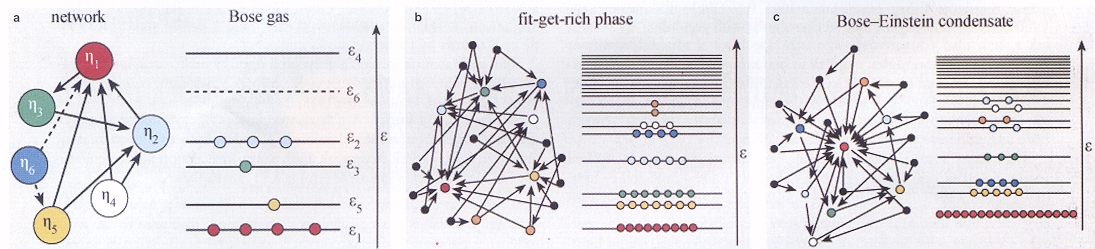
3. ábra. A sematikus ábrázolás a skálafüggetlen-modell fitness-szel kibővített változatát és a Bose-gáz kapcsolatát mutatja (a). A hálózatban minden csomópont véletlenül választott fitness-értéket kap és különböző színekkel jelöltük. A fitness értéke azt mutatja, hogy a csomópont milyen valószínűséggel képes új kapcsolatokat szerezni, a rátermettebb több kapcsolatot létesít, ahogy a hálózat nő. Összerendeltük az energia értéket a csomópontok fitness-értékével az formulát felhasználva, hogy Bose-gázt kapjunk véletlen energiaszintekkel. A leképezésben a rátermettebb csomópont (nagy ) alacsonyabb (kicsi ) értéket eredményez. Egy kapcsolatot a hálózatban i-től j-ig megfeleltethetünk a Bose-gázban egy részecskének az e; energiaértéken. A hálózat fejlődik idővel új csomópont () hozzáadásával, mely két csomóponthoz is kapcsolódik (szaggatott vonal). A Bose-gázban ez megfelel egy új energiaszint hozzáadásának (), és két új részecske hozzáadásának , és energiaszinteken, melyekhez kapcsolódik. Ahogy a hálózat nő, az energiaszintek és a részecskék száma lineárisan nő. A számítás szerint két eset lehetséges, attól függően, hogy milyen eloszlást választottunk az energia szintekből (fitness-értékekből). (b) A “jobb gazdagabb lesz" fázis, ahol nincs tiszta győztes. A részecskesűrűség csökken, ahogy az energiaszint nő. (c) Ezzel ellentétben, ha a Bose-Einstein-kondenzáció veszi át a szerepet, akkor a legjobb csomópont szerzi meg a kapcsolatok jelentős részét. Ez a csomópont erősen telített, míg magasabb energiákon alig van betöltöttség.

4. ábra. A komplex hálózat hiba és kiesés elleni robusztusságát tesztelhetjük, ha megfigyeljük a csomópontok elvételének hatását. (a) A körrel jelölt csomópontok elvétele a hálózat szétesését okozza. (b) A legnagyobb klaszterméret 22-ről 7-re csökken, ha elveszünk három, azaz 14 %-nyi csomópontot. (c) A perkolációelmélet jóslata szerint a véletlen hálózat fc kritikus frakció elvétele után esik szét kis hálózatokra. Ez a jóslat nem érvényes skálafüggetlen-hálózatokra, ahogy az az ábrán látható. A legnagyobb frakció méretét ábrázoltuk az elvont pontok arányában. A számítások azt mutatják, hogy a klaszterméret csak akkor válik nullává, ha minden csomópontot elvonunk (zöld). Habár, ha a legnagyobb fokszámú csomópontokat vonjuk el, akkor a hálózat kis fc értéknél már szétesik. (d) Ha az Internetről véletlenül vonunk el pontokat, akkor úgy találtuk, hogy a pontok 80%-ának elvétele után esik szét kisebb fragmentumokra (zöld). Ha azonban a hackerek a legnagyobb fokszámú csomópontokat támadják meg (piros), akkor ugyanazt a hatást érhetik el a csomópontok kis részét felhasználva.