Fizikai Szemle honlap |
Tartalomjegyzék |
ZONGORAHANGOK ANALÍZISE, KOMPRESSZIÓJA ÉS SZINTÉZISE KARHUNEN-LOEVE-TRANSZFORMÁCIÓVAL
Szalay András
Panda-Audio Kft.
AKAI Professional Musical Instruments Ltd.
A zongora méltán az egyik legnépszerűbb hangszer, hiszen magas fokú polifóniával és széles dinamikatartományban játszható. Széles körű alkalmazásának azonban bizonyos adottságok határt szabnak:
1. Igen súlyos, nehezen szállítható, szállításkor elhangolódik.
2. Egyébként is hangolódik, behangolása komoly szaktudást igényel.
3. Környezeti hatásokra (hőmérséklet, páratartalom) kényes.
4. Lakásban történő használatát behatárolja, hogy nagy és hangos.
5. Drága.
Ezen tulajdonságok miatt kézenfekvőek egy elektronikus zongora előnyei, amelynél a fenti tulajdonságok egyike sem szükségszerű.
Ha egy akusztikus hangszer hangját szintetikusan akarjuk előállítani, két alapvető lehetőség kínálkozik. Egyszerűbb módszer, ha az eredeti hangszer hangjait mikrofonnal felvesszük, és ezt a digitalizált hangot játsszuk vissza a hangszer elektronikus verziójával. Másik, lényegesen bonyolultabb módszer, ha megpróbáljuk a hangszer fizikai működését szimulálni. Ez utóbbi módszer bonyolultsága miatt csak körülbelül az utóbbi 8 évben kezdett elterjedni. Mivel a különböző hangszerek működési elve más és más, mai napig csak az egyszerűbben modellezhető hangszerek fizikai szimulációjára léteznek használható modellek. Például a legtöbb fúvós hangszer hangja ma már fizikai modell alapján is elég jó minőségben előállítható, de a zongora szimulációja egyelőre használhatatlan.
Szerencsére a zongorán leütött hang hangja már a leütés pillanatában meghatározott a leütött billentyű megválasztása és a leütés dinamikája révén, ezen a zenész később már nem tud változtatni (kivéve a pedálok használatát). Ezért a zongora hangja jó minőségben reprodukálható hangminták segítségével, amennyiben megfelelően sok billentyűtartományban (esetleg billentyűnként) és dinamikai szinten veszünk mintákat. Könnyen belátható, hogy ez, például fúvós hangszerek esetében még elvileg sem áll fenn, hiszen a zenész a hang tartása közben is rengeteg módon tudja a hangzást befolyásolni, és ezeknek a lehetőségeknek a követése hangminták közötti váltásokkal lehetetlen lenne.
Ha kiszámoljuk hogy egy kompromisszumoktól mentes zongorahanghoz mennyi memória szükséges, meglepően nagy számot kapunk: 88 billentyű x 8 dinamika szint x átlagosan 8 s mintahossz = 5600 másodperc minta. Az ehhez szükséges memória: 5600 s x 44,1 kHz mintavételi frekvencia x 2 byte/minta = 500 Mbyte. Ugyan a memória ára évről évre elképesztő mértékben csökken, de vegyük figyelembe, hogy itt ROM memóriát kell használjunk (hacsak nem építünk be a gépbe egy harddiszket, ami viszont nem praktikus). A ROM az olcsó RAM-oknál legalább négyszer drágább. Ezért az elektronikus zongorák konstruktőrei trükköket használnak a memóriaigény csökkentésére. Ezek a trükkök természetesen jelentősen befolyásolják a minőséget.
A legfontosabb ilyen trükk, hogy a hangnak csak igen rövid részletét veszik fel, amely részlet alatt a hang spektrálisan erősen változik (0,2-1,5 s), utána az utolsó rezgési periódust ismétlik végtelen hurokban, miközben a hang az eredeti amplitúdó karakterisztikának megfelelően elhalkul. Ennek a módszernek két lényeges hibája van. Egyrészt a spektrum, ha kevésbé is, de mindig folytonosan változik. Másrészt a zongora hangjában, különösen a mély tartományban a hangok felhangjainak frekvenciája eltér az alaphang ideális egészszámú többszörösétől:
![]()
ahol F0 az alaphang frekvenciája, n a felhang indexe, B egy konstans, ami a húr anyagától, de a rezgés amplitúdójától is függ. A végtelenül ismételt hurok értelemszerűen csak az ideális harmonikus felhangszerkezetet tudja visszaadni. Emiatt az így előállított hangban feltűnő, észrevehető, amikor a hang "befagy" a hurokban.
Másik legfontosabb trükk, hogy általában minden billentyűhöz csak egy dinamikaszintű felvétel tartozik forte vagy fortissimo -, az alacsonyabb dinamikájú hangokat úgy állítják elő, hogy vagy egyszerűen halkabb szinten szólal meg ugyanaz a hang, vagy ami egy fokkal jobb, egy vezérelt aluláteresztő szűrő a hangot annál jobban letompítja, minél alacsonyabb dinamika szinten lett a billentyű megütve. Mivel a zongora halk és hangos dinamikájú megszólalása között a spektrális különbség bonyolult, egyszerű szűrővel nem modellezhető, ezért ez az egyszerűsítés lényeges minőségvesztéssel jár.
A WERSI-zongora alapvető terveit négyen készítettük el 1988-89-ben (három fizikus, egy matematikus). A tervek kivitelezésén körülbelül 20 fő dolgozott. Az akkor kialakított koncepciónk megítéléséhez azt is figyelembe kell venni, hogy a memóriaárak akkor még körülbelül 2 nagyságrenddel magasabbak voltak, mint ma, tehát egy kompromisszumoktól mentes hangmintalejátszó-rendszer gazdaságilag teljesen lehetetlen lett volna. Ezért olyan adatkompressziós módszert fejlesztettünk ki, ami lehetővé tette, hogy a hangok keltéséhez felhasznált körülbelül 500 Mbyte hangminta a hangszerben csupán 2 Mbyte-ra komprimálva van jelen.
Az általunk kifejlesztett módszer, amely a Karhunen-Loeve-transzformáció nevű matematikai eljáráson alapul, a matematikai részletek tárgyalása nélkül egy egyszerű gondolatkísérlettel szemléltethető. Először is tételezzük fel, hogy a hang tisztán harmonikus. Ekkor egy hangot előállíthatunk tisztán harmonikus Fourier-transzformációval is, azaz vegyünk annyi szinuszgenerátort, ahány felhangot elő akarunk állítani. Az eredeti hangok analízisével határozzuk meg ezeknek a burkológörbéjét, majd a burkológörbe adatok megengedhető legdurvább időbeni és amplitúdó kvantizálásával csökkentsük le a felhasznált adatmennyiséget. Ezzel a módszerrel egy alapvető baj van: mivel a nem elhanyagolható felhangok száma igen nagy, ez a módszer olyan mennyiségű szinuszgenerátort igényelne, ami messze túl van a realitás határain. Itt azt is vegyük figyelembe, hogy a zongorista legalább 8 hangot tud lenyomni egyszerre, de lenyomott sostenuto-pedál mellett a minimálisan szükséges polifónia ennél is lényegesen nagyobb, legalább 20-30 hang.
A módszer, amit kifejlesztettünk, ezt az igen nagy generátorszámot csökkenti le hangonként maximálisan 8-ra. Ennek az ára csupán annyi, hogy az egyes komponensek jelalakja nem szinusz lesz, hanem valami más; ez viszont a digitális hangkeltés számára teljesen közömbös. Képzeljük el, hogy van egy egyszerű hangunk, aminek csak három szinuszkomponense van, F0, 2 x F0, és 3 x F0, frekvenciával. A hang pillanatnyi spektrumát szemléltethetjük, mint egy pontot egy háromdimenziós koordinátarendszerben, amelynek bázisvektorai a három komponenst reprezentálják. A hang időbeli lefutása ebben a koordinátarendszerben térgörbével ábrázolható, amely valamilyen pályát leírva végül az origóba tart. Könnyen belátható, hogy ha ez a térgörbe adott esetben jó közelítéssel egy a térben kifeszíthető síkon fekszik, akkor egy koordináta-transzformációval elérhetjük, hogy új koordinátarendszerünk első két bázisvektora ezt a síkot feszítse ki. Ebben az esetben a harmadik koordinátát egyszerűen elhagyhatjuk. Tehát ezzel elértük, hogy a generátoraink számát háromról kettőre tudtuk csökkenteni, viszont a generátorok most már nem tisztán szinuszrezgést keltenek, hanem az eredeti komponensek valamilyen lineáris kombinációját, ami a koordináta-transzformációból adódik. A Karhunen-Loeve-transzformáció egy sokdimenziós vektorsokasághoz megkeresi azt a koordináta-transzformációt, amellyel a vektorok az új koordinátarendszerben a lehető legkevesebb bázisvektorral úgy közelíthetők, hogy a közelített értékek négyzetes eltérése az eredeti értékektől a lehető legkisebb legyen. A félig automatizált zongorahanganalízis-program az eredeti hangokból a Karhunen-Loeve-transzformáció segítségével kiszámolja ezeket az új bázisvektorokat, valamint a komponensek burkológörbéit, ezzel létrehozza az adatkompressziót.
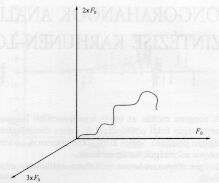
A hang időbeli lefutása origóba tartó térgörbével ábrázolható
Az itt elmondott eljárással csak egy probléma van: mint az a példából is világos volt, ez a módszer csak tisztán harmonikus hangokra alkalmazható. A zongora hangjai két vonatkozásban is lényegesen eltérnek ettől. Az egyik sajátságról már volt szó: a felhangok az alaphangnak nem pontosan egész számú többszörösei. Ez a probléma elhanyagolható a magas hangok tartományában, ahol a hallható felhangok száma alacsony, de igen lényeges a mély tartományban. A másik probléma az, hogy a zongora hangjának igen lényeges alkotórésze kalapácsütésének hangja, ami zajszerű, egyáltalán nem illeszthető a harmonikus spektrumba. Ez a kalapácszaj természetesen a zongora minden hangmagasságában jelen van, azonban korántsem mindenütt hallható. A mély tartományban a spektrum mély részét is igen sűrűn borító felharmonikusok teljesen elfedik a kalapácszajt, így ez itt egyáltalán nem hallható. A magas hangok tartományában egyrészt a spektrum alaphang alatti része eleve nincs elfedve, ezért jól hallható, másrészt a spektrumvonalak távol vannak egymástól, ezért a közöttük levő tartomány tú1 széles, ahhoz hogy akusztikailag teljesen fedve legyen. Ezen okok miatt különböző hangmagasságokban az előbb leírt eljárás különbözőképpen optimalizált verzióit alkalmaztuk.
A mély hangok tartományában a spektrum két részre lett vágva, a két tartományon belül a felhangok sorozatából az analízis program külön-külön számolt ki egy-egy "átlagos" alaphangot. Ebből a magas tartományhoz tartozó rész virtuális alaphangja lényegesen eltért az igazi sorozat alaphangjától. Így a két tartománybeli hangok szuperpozíciója igen pontosan vissza tudja adni a zongora hangjainak élő, folyton picit változó hangzását, aminek pontosan a felhangok eltolódása az oka.
A magas hangok tartományában igen lényeges a kalapácszaj, ami harmonikus módszerrel nem állítható elő. Ezért az analízisprogram szétválasztotta a hangokat harmonikus és nem harmonikus részre. A nem harmonikus kalapácszajnak kicsi a sávszélessége (körülbelül 1500 Hz), ezért ezt alacsony mintavételezési frekvenciával lehet tárolni. Másrészt a kalapácszaj időben rövid, sokkal rövidebb, mint a hang harmonikus része. Az alacsony mintavételezési frekvenciának és a rövid hossznak köszönhetően a kalapácszaj tárolása is igen kevés memóriát igényel.
_______________________________________
Előadás az ELTE Ortvay-kollokviumán. Sajnos az elektroakusztikai bemutatásokat itt nem tudjuk közölni.