Fizikai Szemle 2002/10-11. 297.o.
WIGNER JENŐ NÉMETORSZÁGBAN
- ALAPOZÓ TANULMÁNYOK ÉS KORAI SIKEREK
Helmut Rechenberg
Max Planck Fizikai Intézet, München
Wigner Jenő Pál utolsó gimnáziumi évei az újkori magyar történelem viharos szakaszába estek: 1918 őszén az I. Világháború a szövetséges német és osztrák-magyar birodalom totális katonai vereségével ért véget. Ennek volt egyik folyománya a Magyar Köztársaság megalakulása. Ezt azonban hamarosan szétzilálta előbb Kun Béla kommunista rezsimjének, majd Horthy Miklós tengernagy jobboldali restaurációjának hatalomra kerülése. Végül is 1920 júniusában, a Trianoni Békeszerződés értelmében Magyarország elveszítette területeinek és lakosságának kétharmadát, amely (részben ekkor létrehozott) nemzeti államoknak (Romániának, Csehszlovákiának és Jugoszláviának) jutott. Ily módon Magyarországból (ugyanúgy, mint az osztrák monarchia németnyelvű részéből) két kicsiny ország alakult Közép-Európában.
Nyilvánvaló, hogy - ellentétben a háború előtti helyzettel - a magyarországi tehetséges fiatalok akkori perspektívái a gazdasági és tudományos jövő vonatkozásában egyaránt nem voltak rózsásak és ennek megfelelően a tehetséges fiatalok közül a bátrabbak nagy része külföldi karrier után nézett. Wigner Antal (Jenő édesapja), aki egy Budapest-közeli nagy bőrcserző gyár igazgatója volt, szintén úgy látta helyesnek, hogy Jenő fiát külföldön járatja egyetemre. Úgy tervezte, hogy a hazaiaknál jobbnak vélt Berlini Műegyetemen (Technische Hochschule - TH) a vegyészmérnöki tanulmányokat elvégezve és hazatérve, fia vezető pozíciót foglalhat el a gyárában. Jenő - bár a kutatói pályát előnyben részesítette volna - mégis édesapja terve szerint folytatta tanulmányait, annál is inkább, mivel apa és fia egyetértettek abban, hogy Magyarországon meglehetősen kevés egyetemi tanári poszttal lehetne csak számolni. Így hát Wigner Jenő a Budapesti Műegyetemen végighallgatott első tanulmányi év után Berlinben iratkozott be a TH-ra és ott folytatta a vegyészmérnöki tanulmányait.
Berlin, a kémia (és fizika) fővárosa
A szóban forgó időben Berlin, mint kétségtelenül a kémiai tudományok egyedülálló centruma, több mint szerencsés választásnak számíthatott vegyészi tanulmányok folytatása szempontjából. Igaz, hogy Poroszország Rajna-melléki részeiben és Németország délnyugati tartományaiban jelentősebb volt a nagy vegyi üzemek tömörülése, de az ország fővárosában nagyobb számú intézetben folyt kutatás a kémia minden területén. A Kaiser Wilhelm Institut (KWI) különböző szakosodott egységei és az egyetemek osztozhattak mind tapasztalt szakemberek, mind feltörekvő tehetségek nagy számán, és Wigner, az új magyar diák ebből profitált is. Diplomavezetője, Hermann Mark (1895-1993) például - aki 1922-ben Bécsből került a Berlini Műegyetemre - 1926-ban osztályvezető lett a KWI für Silikatforschungban (és 1927-től 1938-ig külső tudományos munkatárs a KWI für Faserstoffchemie-ben). Doktori munkájának vezetője, Polányi Mihály már 1920 óta dolgozott a KWI für Faserstoffchemie-ben, 1927-ben pedig osztályvezető lett Haber intézetében. Végül Karl Weissenberg (1893-1976), akivel Wigner később együtt dolgozott, a KWI für Physik (Einstein intézetének) tudományos munkatársa volt 1929-től 1933-ig. Sehol másutt, mint Berlinben nem volt olyan szoros kapcsolat a Wigner apja által kiszemelt kémia és a Wignert szerfelett érdeklő modern fizika között.
További említést érdemel, hogy Wigner egyetemi éveiben (valamint ezt követően németországi tudományos karrierjének korai éveiben) a kvantumelmélet húszas években megindult fejlődésének köszönhetően további, minden eddiginél nagyobb mértékben összefonódott a fizika és a kémia.
Wigner beiratkozása idején a TH Berlinen mind az oktatás, mind a kutatás vonatkozásában a gyakorlati alkalmazások követelményei és szempontjai voltak mérvadók: okleveles mérnököket (Diplomingenieur) képeztek a vegyipari technológia minden ágazata részére. A kutatások célja pedig az ipari termelés technológiájának tudományos megalapozása volt. Az újonnan érkezett Wigner annak rendje és módja szerint először a szervetlen kémia alapozó előadásait és az ezekkel párhuzamos gyakorlatokat vette fel. Évek múlva is emlékezett arra és emlegette, hogy a HZS gáz (a klasszikus vegyelemzés fontos reagense, ford. megj.) analitikájával kapcsolatos, részletekre is kiterjedő munkát végzett. Ezek után következtek a szerves kémia és más, a bőrcserzéssel (mint általa szem előtt tartott feladattal) összefüggő tárgyak. Ezek képzésének legfontosabb elsajátítani valója lényegében a legtágabb értelemben vett vegyelemzés módszerei voltak. Wigner azonban mást is megtanult, ami ténylegesen befutott (fizikusi) karrierje során fontosnak bizonyult: "a kémiai analízis elsajátítása közben tudatosodott bennem, hogy a természetben törvények uralkodnak".
Vegyészi tanulmányai mellett Wigner szabad idejének legnagyobb részét otthon töltötte könyvek és cikkek olvasásával, amelyek első sorban elméleti fizika tárgyú, sőt ezen is "túlmenő" művek voltak. Így például Sigmund Freud "Traumdeutung" (Álomfejtés) című könyvének hatására élete végéig tartó érdeklődést tanúsított az emberi tudat problémái iránt. Néha barátok társaságában is olvasott könyveket. Berlinben akkor több honfitársa is élt és járt egyetemre, például Szilárd Leó (1898-1964), aki már 1919-ben kezdte (villamosmérnöki) képzését a TH-n, de fokozatosan fizikussá vedlett át. Wigner a Fizikai Kémiai Intézetben találkozott először Szilárddal és kettőjük között azonnal szoros kapcsolat létesült. Wigner emlékei szerint "Amint Szilárdban tudatosodott, hogy igazán csak a fizika érdekli, a rá jellemző közvetlenséggel Albert Einsteinhez fordult. Azt hiszem, hogy lényegében Szilárdnak köszönhettük, hogy Einstein statisztikai mechanika tárgyú szemináriumot hirdetett, amelyen Szilárdon kívül néhány barátja, köztük Gábor Dénes és én magam is részt vettünk. Einstein virtuozitása egyaránt megnyilvánult abban, ahogyan a valójában megoldatlan problémákra mutatott rá, valamint abban is, ahogyan az elmélet ténylegesen elért eredményeit és szellemét értékelte. A szeminárium legtöbb résztvevője úgy érezhette, hogy rendkívüli élményben részesül, azon kívül pedig Szilárd doktori disszertációjához is inspiráló hatású lehetett."
Wigner is hamarosan személyes kapcsolatba került Einsteinnel csakúgy, mint honfitársa, Gábor Dénes (1900-1978), aki Berlinben (mint Szilárd) villamosmérnöki diplomát (1924), majd doktorátust (1927) szerzett. "Ugyanakkor azonban - mint Gábor 1971. évi Nobel-díjas előadásában megjegyezte - amikor csak lehetett, átosontam a Berlini Egyetemre, amely azokban az években (Einsteinnek, Plancknak, Nernstnek és Lauénak köszönhetően) a fizika fellegvára volt." Wigner vonzódása hasonló lehetett, bár ő nem járt át egyetemi előadásokat hallgatni. Rendszeresen részt vett azonban a híres Berlini Fizikai Kollokviumon, amelyet Max von Laue a következőképpen vezetett. Minden alkalomra Laue kiválasztott négy-öt - az új fizikával kapcsolatosan fontosnak vélt - cikket, a Kollokvium résztvevői közül valakit megkért azok elolvasására, majd a legközelebbi csütörtökön tartandó szóbeli ismertetésére. Ez azt jelentette, hogy az illetőknek meg kellett érteniük a cikkek mondanivalóit, majd a berlini fizikusok előkelő gyülekezete előtt referálniuk. Ilyen előadásokra pedig nem csak híres fizikusok, mint például von Laue és Einstein vállalkoztak, hanem fiatalabb résztvevőket - mint egyszer Wignert is - felkértek. Wigner szerint: "Ezekre a napokra visszaemlékezve, utólag csodálkozom azon, hogy nem idegesített jobban, hogy Einsteinnek és von Lauénak fizikát kell magyaráznom. Túl fiatal voltam ahhoz, hogy felmérjem a kollokvium történelmi jelentőségét. ... Einstein derűs arccal és nyugodt figyelemmel hallgatta az előadásokat." A kollokviumok után Wigner el szokott gondolkozni a hallottakon és utánanézni az irodalomban.
A német főváros 1920-as éveinek minden krónikájában kiemelten szerepelnek politikai és társadalmi nehézségek és azok vetületei, így például Walther Rathenau külügyminiszter 1922 júniusában bekövetkezett meggyilkolása, amely miatt Einstein egy évig kerülte Németországot, vagy a katasztrofális méretű infláció, amely majdnem mindenkit érintett. Wigner ekkor még nem törődött politikával (később annál inkább), anyagilag pedig nem volt érintve, mert pénzét magyar valutában kapta, amelyet értékének megfelelően át tudta váltani.
1924-ben befejezett diplomamunkájának témaköre (a rombos kén rácsszerkezete) meglehetősen komplex röntgen-krisztallográfiai vizsgálatokat tett szükségessé, hiszen a választott kristály elemi cellája nem kevesebb, mint 128 atomot foglalt magában, ámde Wignert sohasem riasztotta vissza a hosszadalmas numerikus munka. A diplomamunkáját vezető Hermann Mark után Wigner doktori disszertációjának konzulense Polányi Mihály lett. Ezen "Statisztikai mechanika és reakciósebesség" című értekezés rövidített változatából Polányival közösen publikált cikk lett. Polányi már huzamosabb idő óta foglalkozott a molekulák képződésének és bomlásának kérdéseivel. "(Polányi) már 1920-as, Karlsruhéban végzett munkái alapján kétségbe vonta az akkortájt ismert, reakciósebességre vonatkozó elméletek helyességét, mivel a két, ellentétes irányú reakcióra kiszámított sebességek összevetése nem adta ki a termodinamika törvényeiből adódó egyensúlyi adatokat." - volt tanítóját és barátját búcsúztató cikkében Wigner így folytatja: "Valójában az ellentétes asszociációs és disszociációs reakciósebességekre vonatkozó első komoly elméletben M. Polányi és E.P. Wigner meghökkentő feltételezésekkel éltek, amelyek azonban később jogosnak bizonyultak. E feltételezések egyike szerint az asszociáció eredményeként létrejött molekulák energiája véges szélességű sávba esik, mely energiasáv
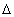 E sebessége a molekulák
E sebessége a molekulák 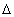 t átlagos élettartamával a
t átlagos élettartamával a 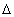 E
E 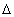 t = h reláció szerint függ össze, ahol h a Planck-állandó." Ez a reláció nem egyéb, mint előfutárja a Heisenberg által két évvel később kimondott határozatlansági relációnak. Ezen túlmenően Wigner disszertációjában egy (további) összefüggést mond ki az ütköző molekulák impulzusnyomatékai és a létrejött molekula nyomatéka között, amelyre Heisenberg nemsokára (1925 nyarán) kvantummechanikájának következményeként is eljut. Így tehát utólag a fiatal magyar vegyész elégedett lehetett a disszertációjával.
t = h reláció szerint függ össze, ahol h a Planck-állandó." Ez a reláció nem egyéb, mint előfutárja a Heisenberg által két évvel később kimondott határozatlansági relációnak. Ezen túlmenően Wigner disszertációjában egy (további) összefüggést mond ki az ütköző molekulák impulzusnyomatékai és a létrejött molekula nyomatéka között, amelyre Heisenberg nemsokára (1925 nyarán) kvantummechanikájának következményeként is eljut. Így tehát utólag a fiatal magyar vegyész elégedett lehetett a disszertációjával.
Kvantummechanika, szimmetria és a Pauli-féle kizárási elv
Doktori oklevéllel a zsebében Wigner 1925 nyarán visszaérkezett Budapestre, hogy édesapja gyárában megkezdje vegyészmérnöki munkáját. Berlinben - még elutazása előtt - Wigner a Német Fizikai Társulat (DPG = Deutsche Physikalische Gesellschaft) egyik összejövetelén megtartotta első előadását. Tagja lett a DPG-nek és előfizette ennek Zeitschrift für Physik (Z. Phys.) folyóiratát, amely akkortájt a legtekintélyesebb fizikai lapnak számított. A Z. Phys. folyamatosan érkező kiadványait esténként rendszeresen olvasva, egy számára egészen új fizikai világot fedezett fel. Egyetemi tanulmányainak évei alatt azt tapasztalta, hogy Berlinben a kvantumelmélet problémáiról mindig úgy beszéltek, mint a távoli jövőben megfejtendő rejtvényekről. Most pedig megállapította, hogy Németország "vidéki" egyetemein, jelesül Göttingában és Münchenben (és néhány más helyen Európában, például Koppenhágában) az atomelmélet rejtélyeinek megfejtése érdekében kifejtett szorgos munka folyt. Felismerte, hogy ennek eredményei messze túlmentek a régi kvantumelméletet reprezentáló, 1910-ben Bohr, Epstein és Schwarzschild által megfogalmazott kvantálási szabályokon, amelyek pedig a húszas években Berlinben még mindig érdemi viták tárgyát képezték Einstein, von Laue, és mások között.
E fordulatról Wigner az alábbi mondatokban emlékszik meg: "Egyik nap fantasztikus cikk jelent meg a Zeitschriftben. Szerzőinek, Max Bornnak és Pascual Jordannak állítása szerint a mikrofizika egyetlen feladata energiaszintek, valamint a szintek között bekövetkezhető átmenetek valószínűségeinek meghatározása. A cikk ezen kívül a Schwarzschild-Epstein féle modell helyett egy matematikailag ellentmondásmentes eljárást javasol fenti mennyiségek kiszámítására."

Wigner azt is megtudta, hogy Born és Jordan előbb említett "A kvantummechanikáról" című cikkének alapgondolata megtalálható egy korábbi cikkben, amelynek szerzője az ugyancsak Göttingában dolgozó Werner Heisenberg volt. A soron következő, a Born, Heisenberg és Jordan szerzőhármas által írt cikket ("A kvantummechanikáról II") pedig Wigner "nagy élményként, kinyilatkoztatásként és a mikrofizika igazi megértéséhez vezető első lépésként" üdvözölte. A cikk mondanivalójának szokatlan mátrixos megfogalmazása nyilván nem zavarta Wignert, aki a kristályszerkezetek leírására használt mátrixokat jól ismerte és kezelte. A továbbiakban nagy figyelemmel kísérte az új kvantummechanika gyors fejlődését, többek között Schrödinger hullámmechanikai megfogalmazásában (amely néhány hónappal később publikálódott), valamint az elmélet csodálatos sikerét, a hélium-atom háromtest-problémájának megoldását.
Itt tartott Wigner, amikor ajánlatot kapott, mely lehetővé tette, hogy a magyarországi bőrcserző ipar gondozását otthagyja a németországi izgalmas fizika kedvéért.
Polányi Mihály benyomásai Wigner Jenő képességeiről olyan jók voltak, hogy volt PhD-diákját Richard Beckernek ajánlotta, aki a TH Berlin újonnan kinevezett tanszékvezetőjeként asszisztenst keresett elméleti fizikai előadásaihoz. A felajánlott fizetés (körülbelül havi 550 márka) "borzasztóan nyomorúságosnak" tűnhetett (egy jól fizetett magyar vegyészmérnöknek) és majdnem ráment az albérletre és az élelmezésre. Wigner édesapja is nyilván fájlalta, hogy fiát elcsábítja a tudomány, de Jenő boldogan elfogadta az ajánlatot és visszament Berlinbe. Professzor főnöke azonnal ráállította egy a bécsi Karl Weissenberggel közösen végzendő kutatómunkára. Weissenberg - az idő tájt a berlini TH-n előadó - azon tűnődött, hogy kristályok az atomok végén miért rendeződnek oly gyakran szimmetriatengelyek vagy szimmetriasíkok mentén. Rövid gondolkodás után Wigner azt felelte: "Azért, mert ha egy rendszernek van szimmetriatengelye vagy szimmetriasíkja, úgy a potenciálnak ott maximuma vagy minimuma van." Weissenberg "elegánsabb" bizonyítást akart volna hallani; erre Wigner nekiült és Heinrich Weber "Az algebra tankönyve" című könyvében (1894) elolvasta a matematikai csoportelmélet elemi ismertetését. Az ennek alapján készült magyarázatot Weissenberg elfogadta, de mindketten túl egyszerűnek találták és nem is kísérelték meg a publikálását.
Csoportelmélet és atomi színképek
1927 őszén Wigner hozzálátott első kvantummechanika tárgyú munkájához. Az atomfizika egyik fontos alapfeladatának megoldására, a hélium-atom energiaszintjének - eredményesnek bizonyult - kiszámítására Heisenberg egy előző, úttörő cikkben bevezette az úgynevezett kicserélődési erőt, amely soktest-problémát reprezentáló atomi rendszerekben lép fel. Wigner azonnal felismerte, hogy "Heisenberg ezen cikke csodálatos, de - néhány más cikkéhez hasonlóan - matematikailag nem teljesen korrekt. Ezért a cikk beható elemzése után mélyebben megvizsgáltam a háromelektronos rendszerekben tapasztalható szimmetria problémáit. Eredményeimet megmutattam Becker professzornak, aki így reagált: "Közöld le! Nagyon érdekes, mellesleg egészen más, mint ahogyan én magam kezelném a problémát." Így hát Wigner megírt egy cikket, amelynek a "Nem-kombináló termek az új kvantumelméletben" címet adta. Lényegében Schrödinger hullámfüggvényeit használta (csakúgy, mint Heisenberg abban a második e tárgyú cikkében, amelyben a hélium energiaállapotait expliciten kiszámította), valamint Paul Dirac (a szimmetrikus és antiszimmetrikus hullámfüggvények, illetve a Bose- és Fermi-statisztikák közötti összefüggésre vonatkozó) eredményeire támaszkodott. Amikor Wigner a hélium-problémát megoldotta, vagyis kiszámította a háromelektronos atomok energiaállapotait, többé-kevésbé Heisenberg és Dirac útját követve hatodrendű determináns-egyenlet gyökét kellett kiértékelnie. Amikor pedig ezt a megközelítést választotta a háromnál több elektront tartalmazó atomok esetében is, felismerte, hogy fejlettebb matematikai módszerekre van szükség. Emiatt egyik, a budapesti gimnáziumban megismert barátjához, Neumann Jánoshoz fordult, aki korábban (1921-től 1923-ig) ugyancsak Berlinben járt egyetemre és - budapesti doktorálása (1926) után - visszajött Berlinbe habilitálás végett. Neumann valóban tudott segíteni. Tanácsára megismerkedett két berlini matematikus (Leo Frobenius és Issai Schur) fundamentális csoportelméleti cikkeivel, "csodálatosnak" és "könnyen érthetőnek" találta őket, és arra a meggyőződésre jutott, hogy az atomszínképek minden szabályossága forgási szimmetriára vezethető vissza. A második, "Nem-kombináló termek az új kvantumelméletben" című cikkében közli is, hogy a forgási csoport irreducibilis reprezentációinak részletes vizsgálata és alkalmazása az, aminek alapján a sokelektronos atomok minden term-rendszerének kvalitatív kiértékelése sikerülhetett.
Wigner ezen új (1926. november 26-án benyújtott) cikkének, valamint Heisenberg hasonló tárgyú (1926. december havában benyújtott) cikkének - amelyben permutációs csoportot használ az atomfizikai soktest-rendszerek leírására - megjelenésével a csoportelmélet gyökeret vert a kvantummechanikában.
Heisenberg ezt követően más irányba fordult, a kvantummechanika fundamentális fogalmaival kapcsolatos problémákkal kezdett foglalkozni. Wigner viszont lankadatlanul folytatta a csoportelmélet alkalmazását spektroszkópiai problémák megoldására és fontos eredményekre jutott. Így például soron következő (1927. május havi) publikációjában többek között levezeti Otto Laporte híres félempirikus szabályát és felfedezi, hogy az atomelméletben egy fontos szimmetriaelv érvényesül: "Ismertem a spektroszkópai szabályokat; Laporte szabálya történetesen emlékeztetett az inverzió elméletére - mindebből pedig könnyű volt az időinverzió szabályára következtetni." Cikkének végén büszkén megállapítja, hogy "viszonylag egyszerű, szimmetriával kapcsolatos megfontolások alapján a Schrödinger-egyenlettel a tisztán kvantitatív spektroszkópiai tapasztalatok nagy része megmagyarázható."
Egy év Göttingában: együttműködés Jordannal a kvantum-térelméletben
1927. május havában Arnold Sommerfeld levelet írt David Hilbert göttingai matematikusnak, aki új fizikus asszisztens után nézett, mivel eddigi asszisztense, Lothar Nordheim az angliai Cambridge-be készült (Rockefeller ösztöndíjjal): "Ami az asszisztensi állást illeti, én most nagyon alkalmas embert tudok Önnek ajánlani. Neve: Dr. Wigner, jelenleg asszisztens Richard Beckernél. Wigner matematikában nagyon erős, és minden ebbéli tudását önnön erejéből szerezte meg. A Zeitschrift für Physikben publikált dolgozatai Heisenberg régebbi cikkeiből indulnak ki és részben elébe vágnak későbbi eredményeinek. Becker is érdekelt Wigner matematikai továbbképzésében és hozzájárulna ahhoz, hogy Wigner egy évig Önnél dolgozzék."
Megállapíthatjuk, hogy most sem Hilbert asszisztensének fizetése volt az, ami Göttingába csábította Wignert, hanem az a közismert tény, hogy akkoriban Hilbert számított a világ legnagyobb matematikusának. Wigner boldogan elfogadta ezt az ajánlatot. Sajnálatos módon Hilbert a következő évben sokat betegeskedett, ezért Wigner csak nagyon kevés alkalommal találkozhatott vele, a remélt intenzív együttműködés nem alakulhatott ki.
Másrészt azonban Göttinga a modern atomfizika egyik fontos centrumának számíthatott Max Bornnal és James Franckkal az Egyetem elméleti, illetve kísérleti fizikai intézetének élén és a kutatás élvonalában. Az újonnan érkezett Wigner hamarosan megszerette Bornt, akinek kitűnő munkatársaival (jelesül Pascual Jordannal és Walter Heitlerrel, aki nemrég Zürichből, Schrödinger mellől érkezett Göttingába), valamint Born nagy nevű, Göttingában vendégeskedő fizikus ismerőseivel is lehetett tartalmas eszmecseréket folytatni.
A keményen dolgozó Wigner Neumann-nal közösen is alkotott és publikált. (Neumann azokban a napokban szintén gyakori vendég volt Göttingában, miután az előző akadémiai évet ott töltötte és Hilberttel, valamint Nordheimmel együtt könyvet írt a kvantummechanika matematikai alapjairól. Neumann később egyedül is több cikket írt, amelyben korábbi eredményeit matematikai értelemben szigorúbban - vagyis axiomatikus alapon fogalmazta meg és általánosította.)
Az atomszínképek szimmetriák alapul vételével történő leírását Wigner Göttingában is folytatta, méghozzá egy háromrészes dolgozatban, amit Neumann-nal együtt "A perdülő elektron kvantummechanikája" címmel publikált. A szerzők ambiciózus célkitűzése nem kevesebb, mint az atomszínképek teljes szerkezetének meghatározása, mégpedig a Dirac Jordan-féle statisztikai transzformáció-elméletnek, a Neumann-féle axiomatika eredményeinek, valamint az atomrendszerek mindenféle tértranszformációval (különösen: rotációival) szemben mutatott invarianciájának alapján. Wigner későbbi interjúk során beismerte: "A cikket elsősorban én írtam, de úgy éreztem, hogy kifejezésre kell juttatnom Neumann iránti hálaérzeteimet azért, hogy Frobenius és Schur munkáival megismertetett. Ezért javasoltam, hogy együtt publikáljunk. Neumann csodálatos matematikus volt: nem ismertem nálánál gyorsabb észjárású és tájékozottabb matematikust." Wigner ezen kívül egy akkortájt divatos területen (a kétatomos molekulák színképeiről van szó) kezdett dolgozni, mégpedig egy másik vendégkutatóval, az amerikai Enos E. Witmerrel együtt. Itt is a csoportelméleti megközelítés módszerét alkalmazta.
Wignerrel körülbelül egy időben Pascual Jordan is visszaérkezett Göttingába egy a Niels Bohr koppenhágai intézetében töltött félév után, amely alatt Oskar Kleinnel együtt a bozonok nemrelativisztikus kvantum-térelméletének kidolgozásán fáradozott. Jordan most Wignerrel társult annak érdekében, hogy a fermionok (például a Pauli-féle kizárási elv hatálya alá eső elektronok) esetére hasonló formalizmust kapjanak. Az együttműködés kiválóan sikerült; a szereposztást, illetve az érdemszerzésben való részesedést Wigner a következőképpen jellemezte: "Jordané az alapötlet, amelynek megvalósítását közösen publikáltuk. Tőlem származik viszont annak matematikailag korrekt bizonyítása, hogy a kommutátorok helyett anti-kommutátorok alkalmazása fermionok kvantálására az egyetlen mód ahogyan a Pauli féle kizárási elv megmagyarázható."
Jordan és Wigner azzal is próbálkoztak - sikertelenül -, hogy az elektron relativisztikus egyenletét megtalálják. Amikor Born 1928-ban megmutatta Dirac levelét az elektron új egyenletével, Jordan így szólt Wignerhez: "Csodálatos egyenlet! Kár, hogy nem mi találtuk ki, de természetesen nagyon jó, hogy valaki megtalálta."
Born intézetében Wigner az amerikai Robert Oppenheimerrel is megismerkedett, aki itt készítette doktori disszertációját. Jenő azonban leginkább Jordan és Heitler társaságát kedvelte, akikkel a kollokviumok után ebédelni szokott, amikor is "megvitattuk a kollokviumon felmerült kérdéseket. Az ilyen megvitatások nemcsak hasznosak, mert ilyenkor sokat lehet tanulni másoktól, hanem azért is, mert vita közben az ember arra kényszerül, hogy saját nézeteit világosabban fejtse ki. Erre pedig Göttingában sok alkalmam adódott." 1928 vége táján, egy évnél valamivel hosszabb távollét után Wigner erőben gyarapodva visszatért Berlinbe, ahol állása volt.
Az utolsó berlini szakasz
Berlinbe történt visszatérése után Wigner hamarosan habilitált. A fizikai tudományok terén időközben alapos változások álltak be: Először is azért, mert új, fiatal kollégák jelentek meg, akik megismerkedtek az új atomelméletekkel és ezeknek továbbfejlesztésében is részt vettek. Másrészt Erwin Schrödinger, a hullámmechanika felfedezője az Egyetem elméleti fizika professzoraként utódja lett a nyugállományba került Max Plancknak. Így tehát a modern atomelmélet Berlinben már megfelelő képviselettel rendelkezett - annak ellenére, hogy Einstein, Planck és Schrödinger filozófiai alapon még mindig ágáltak a kvantummechanika statisztikai értelmezése ellen, amelyet a Göttinga-Kopenhágai iskola (és annak védelmezői: Born, Heisenberg és Bohr) képviselt.
A TH-n Wigner az 1928/29 téli szemeszter elején "Atomszerkezet és kvantumelmélet" címen hirdetett kurzust, amelyet a következő, nyári szemeszterben is folytatott, mégpedig feladatmegoldó gyakorló órákkal kiegészítve. 1929. december hó 9-én távirat érkezett: "Princeton februártól júniusig szóló előadói megbízást ajánl Önnek. A honorárium és a költségtérítés együtt összesen 3000 $. A felszólítást igazoló levél útban van. Szíveskedjék válaszát táviratban megküldeni." A híres amerikai egyetem ezen bőkezű ajánlata meglepte Wignert, akinek akkori berlini fizetése havi 80 $-nak felelt meg, szemben az amerikai 3000 $-ral. Ezért először azt hitte, hogy a szám téves, azonban Neumann is kapott hasonló táviratot az övével megegyező számmal. Igaz ugyan, hogy az utazások költségeit a honoráriumból kellett fedeznie és hogy az Egyesült Államokban magasabbak voltak a megélhetési költségek, de a két magyar tudós így is megelégedéssel vehette tudomásul a meghívásban megnyilvánuló nagyrabecsülést. Wigner és Neumann később megtudta, hogy a meghívást Paul Ehrenfest professzornak köszönhetik, aki munkatársait olyan amerikai egyetemekre ajánlotta, amelyek a modern atomelmélet oktatásának színvonalát óhajtották emelni. A két magyar végül is nagy kedvvel vágott neki az amerikai kalandnak. A Princeton Egyetem viszont nagyon is elégedett lehetett velük, mert néhány hónappal a megérkezésük után a fizikusi kar egyik bizottsága azzal a közléssel állt elő, hogy mindkettőjüket professzori állásban alkalmaznák; a nős Neumann-nak évi 5500 $-t, a nőtlen Wignernek pedig 4500 $-t ajánlottak. A magyarok azzal az ellenjavaslattal válaszoltak, hogy mindketten félévi megbízatást vállalnának, úgy hogy a "másik" félévben Németországban dolgozhatnak. Az amerikaiak bizottsága elfogadta ezt az ellenjavaslatot.
Wigner 1931 tavaszán állt munkába, Neumann pedig 1931 őszén érkezett, ily módon ingázva a nyugodt Princeton és a turbulens Berlin között. Wigner valahogyan még 3 szabad hónapot biztosított magának magyarországi üdülés céljára.
A Göttingában töltött év után Wigner gyorsan visszaszokott Berlinhez, a mozgalmas kollokviumokhoz és nagyszámú ottani barátjához. Hírneve egyre növekedett. Együttműködött és további tudományos cikkeket publikált kollegákkal, beosztott munkatársakkal, de egyedül is.
1928-ban például, Polányival (volt PhD-vezetőjével) közösen írt és publikált egy második cikket fizikai-kémiai folyamatokról, 1932-ben H. Peltzerrel együtt egy cikket a kémiai reakciók sebességi állandóiról, valamint néhány - inkább matematika tárgyú - cikket Neumannnal együtt (az egyiket például adiabatikus folyamatokban változó energia-sajátértékekről).
Fenntartotta a Göttingai Elméleti Intézettel kialakult szívélyes kapcsolatot és Born egyik diákjával, Victor Weisskopffal közösen írt két dolgozatot, a kvantum-térelmélet két elhíresült dolgozatát a természetes vonalszélességről, amely Weisskopf 1931. évi doktori dolgozatának egyik előfutára.
Nagyobb lélegzetű vállalkozás egyik eredménye lett a "Csoportelmélet és alkalmazásai az atomszínképek kvantumelméletében" című könyv. Szilárd Leó és Max von Laue olyan magasra értékelték Wigner csoportelméleti módszereinek atomfizikai alkalmazásait, hogy kérlelték, írjon ilyen tárgyú tankönyvet. Ehhez tudni kell, hogy hasonló könyv ("Csoportelmélet és kvantummechanika") már létezett a piacon. Írója a jól ismert zürichi matematikus (egy ideig Hilbertnél diák) Hermann Weyl (1885-1955) volt, aki maga is úttörő munkát végzett a modern matematikai csoportelmélet megalapozásában.
Első cikkét a csoportelméleti módszerek atomfizikában történő alkalmazásáról körülbelül egy évvel Wigner után publikálta. A "baj" a tankönyvével azonban az volt, hogy fizikusok - különösen pedig az egyetemi hallgatók - igen nehezen boldogultak a tömör és nagyon is magas szintű szöveggel, amelynek fő feladata a matematikai csoportelmélet szerkezetének és annak az új kvantummechanikával felfedett szoros kapcsolatának bemutatása volt.
1928-ban a csoportelmélet valóban már igen hasznos matematikai eszköznek számított az atom- és molekulaelméletben. (Az utóbbi munkaterületen való alkalmazás két úttörője Göttingában Friedrich Hund, Zürichben pedig Walter Heitler volt).
Ugyanakkor azonban ellenzői is akadtak az úgynevezett "csoportpestis"-nek: a fizikusok egy része rossz szemmel nézte a "szokatlan" matematikai eszközök elterjedését a kvantummechanikában és "száműzni" akarták belőle. Ezen igyekezet ellen Hermann Weyl könyvének (második, 1930 novemberében megjelent) kiadásához írt előszavában így érvel: "... ez (a száműzés) biztosan nem lehetséges, ha a rotációkról és a Lorentz-csoportról van szó. Ami a permutációs csoportot illeti, valóban mellőzhető a Pauli-elvre való hivatkozással. De akkor sem nélkülözheti az elmélet a permutációs csoport reprezentációit, mint természetes eszközt, amely megkönnyíti a spin bevezetésének tulajdonítandó relációk megértését." Weyl ezután hangsúlyozza, hogy könyvében a matematikai tárgyalás módszerének említésére szorítkozik és szándékosan nem sorolja fel azt a nagyszámú alkalmazást, amely Hartree, Slater, Dirac és mások szellemes módszerén alapul.
Így hát annak ellenére, hogy már létezett Weyl azonos tematikájú könyve, Wigner egyetérthetett Szilárddal és von Lauéval abban, hogy egy második könyvre is szükség van, amely az elmélet egyes részleteivel és gyakorlati alkalmazásaival foglalkozik. Szilárd meggyőzte barátját, hogy ilyen könyv - ha könnyebb olvasmány, mint Weylé - megfelel mind a diákok, mind pedig az atomspektroszkópia specialistái igényeinek és ajánlotta, hogy a könyvben Wigner mind saját munkáját, mind annak eredményeit is mutassa be. Wigner célkitűzései könyvének összeszerkesztésénél - amelyet azzal fejezett be, hogy 1931 februárjában aláírta az előszót - valóban teljesen eltérők Weyl komplementárisnak nevezhető megközelítésétől. Wigner célja lényegében a fizikusok (és kémikusok) széles körének tájékoztatása egy módszerről, amely sokelektronos rendszerek hullámmechanikai egyenleteinek megoldására alkalmas, továbbá annak a bemutatása, hogy egyes partikuláris szimmetriaműveletek hogyan segítik lényegesen a megoldást. A "Gruppenpest"-tel szemben megnyilvánult ellenszenvet pedig annak hangsúlyozásával próbálja eloszlatni, hogy a szimmetriával kapcsolatos elemi megfontolások szükségképpen közelebb állnak a fizikai szemlélethez, mint a számítások. Ugyanezen okból Wigner "közelről" bemutatja a csoportelméleti formalizmus néhány "apró" részletét, mégpedig egyes példák elemzésével. A példák összeválogatásánál atomfizikai alkalmazására szorítkozik, mert "fontosnak látja egyetlen fizikai részterület minél teljesebb bemutatását, nem engedvén annak a csábításnak, hogy különböző munkaterületek legszebb engedményeit áttekintse". Wigner könyve egyaránt hasznos az egyetemi hallgatóknak és a gyakorlat embereinek: bevezeti olvasóit azon csoportelméleti módszerek világába, amelyek atomszínképek rendszerezésénél és kiszámításánál alkalmazásra kerülhetnek.
Wigner szakmai perspektívái, az új politikai helyzet Németországban
Amikor Wigner hozzálátott első könyvének megírásához eszébe juthatott Szilárd Leó tanácsa, hogy ne felejtse ki a könyv szövegéből saját tudományos eredményeinek ismertetését. Wigner ugyanis ekkor már nem láthatta eleve biztosítottnak a saját németországi egyetemi és/ vagy kutatóintézeti karrierjét.
A harmincas évek elején tovább romlott a helyzet, amit természetesen nem csak a tudomány emberei, hanem az egész lakosság érzékelhetett. A depresszió által sújtott Németországban a munkanélküliek száma több millió volt. Ehhez járult még a Weimari Köztársaság politikai rendszerének eróziója. Ahogy a szélsőséges politikai pártok tagjainak és szavazóinak száma egyre nőtt - ez kommunistákra és nemzeti szocialistákra egyaránt vonatkozott -, a fejlemények katasztrófa irányába mutattak.
Wigner ekkor kezdte magát rosszul érezni Németországban. Politikai nézeteit osztotta Szilárd Leó. Mindketten attól is tartottak, hogy a kommunizmus egész Európára kiterjeszti hatalmát - amiből némi ízelítőt körülbelül tíz évvel korábban kaptak is saját országukban -, de ugyanannyira az új fasizmustól is tartottak, amely soha nem látott mértékben agresszív antiszemitizmussal párosult. A két magyarhoz 1928-ban egy harmadik, velük azonos nézeteket valló kolléga csatlakozott. Teller Ede 1925-ben került Budapestről Karlsruhéba (egyébként ugyancsak vegyészmérnöki tanulmányok elvégzésének szándékával). Ő is fizikára váltott át (Münchenben, Sommerfeld hatása alatt) és "végül" Lipcsében Heisenberg tanítványa lett. Wigner 1928-ban találkozott először Tellerrel, akivel szoros - bár kissé rendhagyó - barátság alakult ki. Két vonatkozásban azonos nézeteket vallottak: egyrészt Heisenberg kvantummechanikájának odaadó hívei lettek (Heisenberg lipcsei szemináriumainak résztvevőiként rendszeresen találkoztak is). Másrészt politikai állásfoglalásukban is egyformán gyűlölték a kommunista és fasiszta diktatúrákat és később egyesítették is mindkét rendszer ellen forduló erőfeszítéseiket.
1932-től kezdődően Németországban a politikai helyzet rohamosan éleződött, amint a náci párt közelebb került a hatalomátvételhez - először Poroszországban, majd az 1933. január havi választáson a Birodalomban. Emiatt a kivándorlást választotta sok nemzetközileg híres (Albert Einstein, Max Born), valamint csak később elhíresült kolléga. Wigner sok barátja a náci kormány által 1933 márciusában hozott antiszemita törvény nyomán távozott. Ebben a hónapban Wigner még benyújtott egy dolgozatot (neutronoknak protonokon történt szóródásáról) a Zeitschrift für Physikhez - évtizedekre az utolsót. Ez a cikk egyben azt is jelezte, hogy Wigner a fizikának egy újabb területére lépett, amelyben hamarosan úttörő munkát végzett, nem utolsó sorban azoknak a csoportelméleti módszereknek és fizikai-kémiai ismereteknek köszönhetően, amelyeket Németországban szerzett meg és gyakorolt először.
Utóirat
1961. október 16-án, Bécsben, az Osztrák és a Német Fizikai Társulat közös rendezvényén Wigner Jenő átvette a Max-Planck-Érmet, amelyet elméleti elsősorban a fizikában megfigyelt szimmetriákkal kapcsolatos - munkájáért ítéltek neki. Friedrich Hund, akit Németországban az atom- és molekulaelmélet nagymestereként tiszteltek, laudációjában így nyilatkozott: "Az idősebb nemzedék még mindig számon tartja azt a meglepetést, amelyet 1926-ban és 1927-ben az Ön feltűnése a kvantumelmélet központi kérdéseivel foglalkozó fizikusok körében váltott ki."
Jelen beszámoló szerzője részt vett az ünnepségen, Wignert magát ott látta és hallgatta először. Később Európában és az Egyesült Államokban több alkalommal találkozott vele, amikor is közelebbről is megismerhette e nagy fizikus széles, tudományos és egyéb tárgyú érdeklődési körét és megszerette meleg, udvarias és tiszteletet parancsoló személyiségét.
______________________________
Előadás a Magyar Tudományos Akadémián (2002. november 8.). Fordította: Haiman Ottó.
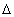 E sebessége a molekulák
E sebessége a molekulák 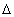 t átlagos élettartamával a
t átlagos élettartamával a 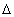 E
E 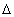 t = h reláció szerint függ össze, ahol h a Planck-állandó." Ez a reláció nem egyéb, mint előfutárja a Heisenberg által két évvel később kimondott határozatlansági relációnak. Ezen túlmenően Wigner disszertációjában egy (további) összefüggést mond ki az ütköző molekulák impulzusnyomatékai és a létrejött molekula nyomatéka között, amelyre Heisenberg nemsokára (1925 nyarán) kvantummechanikájának következményeként is eljut. Így tehát utólag a fiatal magyar vegyész elégedett lehetett a disszertációjával.
t = h reláció szerint függ össze, ahol h a Planck-állandó." Ez a reláció nem egyéb, mint előfutárja a Heisenberg által két évvel később kimondott határozatlansági relációnak. Ezen túlmenően Wigner disszertációjában egy (további) összefüggést mond ki az ütköző molekulák impulzusnyomatékai és a létrejött molekula nyomatéka között, amelyre Heisenberg nemsokára (1925 nyarán) kvantummechanikájának következményeként is eljut. Így tehát utólag a fiatal magyar vegyész elégedett lehetett a disszertációjával.