
Fizikai Szemle honlap |
Tartalomjegyzék |
Fizikai Szemle 2003/4. 122.o.
Horváth Dezső
MTA KFKI RMKI és MTA ATOMKI
Szimmetriák és megmaradási törvények
A szimmetriák a részecskefizikában még fontosabb szerepet játszanak, mint a kémiában vagy a szilárdtestfizikában. Amíg az utóbbiakban az anyagok fontos tulajdonságai vezethetők vissza a különböző atomi, molekula- és kristályrács-szimmetriákra, a részecskefizikában gyakorlatilag minden a szimmetriákból (vagy azok sérüléséből) származik: a megmaradási törvények, a kölcsönhatások, sőt a részecskék tömege is.
Szimmetriák vezetnek a megmaradási törvényeinkhez. Az energia- és impulzusmegmaradás levezethető abból a kézenfekvő szimmetriából, hogy a fizikai törvények nem függhetnek attól, hol vesszük fel az időskálánk és koordinátarendszerünk kezdőpontját, az impulzusmomentum megmaradása (amely többek között egyenesen tartja menet közben a biciklinket) pedig a koordinátarendszerünk tetszőleges szögének következménye. Az elektrodinamika egyenletei, a Maxwell-egyenletek mértékszimmetriája - amely az elektrosztatikus tér esetében a potenciál zéruspontjának szabad választását jelenti - vezet az elektromos töltés megmaradásához, a fermionok mozgását leíró Dirac-egyenlet hasonló szimmetriája pedig általában a fermionok számának megmaradásához. A legtöbb szimmetria valamilyen megmaradási törvényhez vezet, a vonatkozó megmaradási törvények pedig a kölcsönhatások fontos jellemzői, ezért is olyan fontos a szimmetriák felderítése.
Fermionok és bozonok
Az elemi részecskéket különféle szempontok szerint osztályozzuk. A legfontosabb a spin (saját impulzusmomentum) szerinti: a feles spinű (S = 1/2; 3/2; 5/2..) fermionok és az egész spinű (S = 0; 1; 2...) bozonok szimmetria- és egyéb alapvető tulajdonságai erősen különböznek. A fermionok száma megmarad, míg bozonokat büntetlenül kelthetünk vagy elnyelethetünk: egy lámpa akárhány látható bozont (fotont) kisugározhat és egy vevőantenna akárhányat elnyelhet, csak az energia és az impulzus, megmaradását kell biztosítanunk. Ugyanakkor a televízió képernyőjét felvillantó elektront, amely fermion, valahonnan oda kell vinnünk, és dolga végeztével valahová el kell vezetnünk. Érdekes és a fizika szempontjából igen lényeges különbség az is, hogy adott állapotban akárhány bozon lehet egyidejűleg, de fermionból csak egy (Pauli-elv). Ennek következtében töltenek az atomi elektronok egyre növekvő energiájú energiahéjakat, és ez akadályozza azt meg, hogy az atomok az anyagban és a nukleonok az atommagban egymásba hatoljanak; az előbbi biztosít makroszkopikus formát tárgyainknak.
A feles és egész spinű részecskék alapvetően különböző szimmetriájúak: a fermionok fizikai viselkedését leíró hullámfüggvény két azonos fermion felcserélésekor előjelet vált, szemben a bozonokéval, amely nem vált előjelet, és a korábban tárgyalt fermion-bozon különbség innen vezethető le. A részecskék spinje is furcsa szerzet; habár hozzáadódik a részecskék hagyományosabbnak tekinthető pályamomentumához, amely a különböző atomi pályákon elhelyezkedő (de nem igazán keringő) elektronok alapján kapta a nevét, az elektron esetén csak két fizikai sajátállapota van: vagy jobbra forog (azaz a spinje felfelé mutat), vagy balra (lefelé), és ez vezet a spin igencsak különös szimmetriatulajdonságaihoz.1
Részecskék és antirészecskék
A részecskéknek általában van antirészecskéjük, amely azonos tulajdonságú, de ellentétes töltésű, és kölcsönhatásuk annihilációt, sugárzásos megsemmisülésüket eredményezi. A részecske-antirészecske aszimmetria oka a Világegyetemben - azaz az, hogy miért nincs a mi világunkkal egyenértékű, de antianyagból álló antivilág - a fizika nagy kérdései közé tartozik, Ha lennének ugyanis antianyagból álló csillagrendszerek, azok antirészecskéket sugároznának. A galaxisok és antigalaxisok határán, ahol az egyik galaxis kibocsátotta részecskék a másik anyagával szétsugároznak, erős sugárzási zónát kell látnunk, de a csillagászok sehol sem észlelnek ilyen jelenséget.
Az antirészecskék érdekes tulajdonsága, hogy matematikailag úgy kezelhetők, mintha azonos tömegű, azonos nagyságú és ellentétes előjelű töltéssel rendelkező, térben és időben ellenkező irányban haladó részecskék volnának. Ez a természet fontos szimmetriája: a töltés, s tér és az idő egyidejű tükrözésétől a fizika törvénye nem változnak meg. A három tükrözési művelet angol rövidítése nyomán (charge, parity, time) ezt CPT-szimmetriának hívjuk. Az elektron és pozitron ütközésekor végbemenő folyamatokat tehát úgy írhatjuk le, mintha egy elektron bejönne a képbe, valamit csinálna, az dolga végeztével, térben és időben ellenkezőleg kihátrálna; az elektromágneses áram analógiájára ezt részecskeáramnak nevezzük.
Egyszerű részecskeütközés esetén egy ilyen oda-vissza menő részecskeáram kölcsönhatási bozont cserél egy másik hasonló árammal. Ezt Heisenberg határozatlansági relációja teszi lehetővé, amelynek értelmében egészen rövid időtartamokra, illetve távolságokon megengedett az energia-, illetve impulzusmegmaradás sérülése:
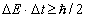 és
és 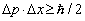 , ahol
, ahol
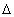 az utána álló mennyiség (kis) változását jelöli, E, p, t és x
a szóban forgó részecske energiáját, impulzusát, az eltöltött időt és a megtett úthosszat. A 2
az utána álló mennyiség (kis) változását jelöli, E, p, t és x
a szóban forgó részecske energiáját, impulzusát, az eltöltött időt és a megtett úthosszat. A 2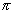 -vel osztott
Planck-állandó,
-vel osztott
Planck-állandó, 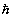 = 1,055
= 1,055  10-34 J/s kicsinysége biztosítja, hogy a makrovilágban a megmaradási törvények pontosan teljesülnek. A cserebozon lehet tehát valódi vagy virtuális aszerint, hogy teljesül-e rá az energia- és impulzusmegmaradás, azaz ténylegesen (kísérletileg megfigyelhetően) létrejön-e vagy sem.
10-34 J/s kicsinysége biztosítja, hogy a makrovilágban a megmaradási törvények pontosan teljesülnek. A cserebozon lehet tehát valódi vagy virtuális aszerint, hogy teljesül-e rá az energia- és impulzusmegmaradás, azaz ténylegesen (kísérletileg megfigyelhetően) létrejön-e vagy sem.
A CPT-szimmetria annyira alapvető a térelméletben, hogy sokak szerint nem is lehet kísérletileg vizsgálni; látszólagos kis eltérések megfigyelése esetén inkább hihetünk valamelyik megmaradási törvény sérülésében, mint a CPT-szimmetriáéban. Ennek ellenére komoly kísérleti erőfeszítés irányul ellenőrzésére. Legfontosabb tesztje a semleges K-mezon és antirészecskéje relatív tömegkülönbsége, amely a mérések szerint < 10-18. A CERN-ben 1999 végén megépült Antiproton-lassító berendezés fő célja antihidrogén-atomok (antiproton és pozitron kötött állapota) előállítása, hogy a hidrogénatommal összehasonlítva a CPT-szimmetriát ellenőrizzék. Az antiproton tömegét például két különböző kísérlet eredményéből sikerült nagy pontossággal meghatároznunk: mágneses csapdában keringő antiproton ciklotronfrekvenciája a (töltés/tömeg) arányt, az elektron helyén atomi pályára fogódott antiproton atomi átmeneteinek energiája pedig a (töltés a négyzeten x tömeg) szorzatot határozta meg.
Leptonok és kvarkok
A részecskék másik osztályozási szempontja az, hogy a jelenleg ismert négy alapvető kölcsönhatás, a gravitációs, elektromágneses, gyenge és erős közül melyekben vesznek részt. Mivel a gravitáció szerepe csak csillagászati szinten jelentős - habár valamennyi részecskére hat -, laboratóriumi szinten elhanyagolhatjuk. Ugyancsak minden részecskére hat a gyenge és minden töltéssel vagy mágneses momentummal rendelkezőre az elektromágneses kölcsönhatás. Az erős kölcsönhatásban résztvevő részecskéket hadronoknak, közöttük a fermionokat barionoknak, a bozonokat pedig mezonoknak hívjuk. Az erős kölcsönhatásban részt nem vevő részecskék a leptonok. A nevek a kezdetben megfigyelt részecskék tömegéből erednek: a leptonok (például az elektron) könnyűek, a mezonok (például a pion,
m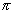 ~ 139
MeV,2 az elektron tömegének, me = 0,511 MeV, 273-szorosa) közepes tömegűek, míg a barionok (proton, neutron) nehéz részecskék (mp = 938 MeV ~ 1836 me).
~ 139
MeV,2 az elektron tömegének, me = 0,511 MeV, 273-szorosa) közepes tömegűek, míg a barionok (proton, neutron) nehéz részecskék (mp = 938 MeV ~ 1836 me).
Az egyik legkorábbi megfigyelés, amely az elemi részecskék lehetséges belső szerkezetére mutatott, a proton és a neutron hasonlósága volt: csaknem azonos a tömegük és azonosan hat rájuk az atommagot összetartó erős kölcsönhatás, csak a töltésük különbözik. Bevezették tehát a nukleon fogalmát, amelynek két állapotát, a neutront és a protont az izospin kvantumszám3 különbözteti meg. Az izospin a spinhez hasonló vektor: a nukleon két állapottal rendelkezik, a felfelé mutató izospint rendeljük a protonhoz, a lefelé mutatót a neutronhoz. A spinhez csak annyi köze van, hogy azonos szimmetriacsoport, az SU(2) írja le a tulajdonságait. Az izo előtag magfizikai eredetű: adott protonszámú elem különböző neutronszámú izotópjai, illetve az adott tömegű, tehát azonos teljes nukleonszámú, de különböző protonszámú izobár-állapotok az izospin segítségével azonosíthatók.
A kísérleti technika javulásával egyre több erős kölcsönhatásban résztvevő elemi részecskét, hadront fedeztek fel; és valamennyi rendelkezett izospinnel. A nukleon izospinje I = 1/2 , a harmadik komponense I3 = 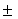 1/2 lehet a két állapotnak megfelelően. A legkönnyebb hadron, a
1/2 lehet a két állapotnak megfelelően. A legkönnyebb hadron, a 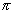 -mezon vagy pion izospinje 1, a három lehetséges sajátállapotnak (I3 = -1, 0 és +1) megfelelően háromféle töltésű pion létezik, pozitív, semleges és negatív. Az izospin tehát az elemi részecskék osztályozásának alapvető kvantumszáma lett.
-mezon vagy pion izospinje 1, a három lehetséges sajátállapotnak (I3 = -1, 0 és +1) megfelelően háromféle töltésű pion létezik, pozitív, semleges és negatív. Az izospin tehát az elemi részecskék osztályozásának alapvető kvantumszáma lett.
Azt követően, hogy felfedeztek egy újabb kvantumszámot, a ritkaságot (angolul strangeness), amely az izospinnel újabb és újabb hadronokban szabadon kombinálódik, Gell Mann és Zweig bevezették a hadronok kvarkmodelljét. Három kvark feltételezésével sikerült leírni az összes addig megfigyelt részecskét. Az első két kvark az I3 = 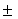 1 sajátértékének megfelelően az up (fel) és down (le) nevet kapta, a harmadik pedig a strange nevet. Jelölésük ennek megfelelően u, d és s. A kvarkmodell szerint a kvarkok kétféleképpen kapcsolódhatnak össze: három kvark bariont (és három antikvark antibariont), illetve egy kvark és egy antikvark mezont formál. A kvarkok spinje feles
(1. táblázat), tehát fermionok. Három kvark kötött állapota is fermion lesz tehát, míg a kvark+antikvark rendszer bozon. A kvarkok töltése
+2/3 és -1/3, így adja ki például a p = (uud) állapot a proton pozitív és az n = (udd) a neutron zérus töltését. Az izospin harmadik komponense tehát az u- és d-kvark töltésével van szoros összefüggésben, egységnyi növelése ugyanis azt jelenti, hogy az adott részecskében egy d-kvarkot u-kvarkra cserélünk, tehát a töltését egységgel növeljük: + 2/3 - (-1/3 ) = 1.
1 sajátértékének megfelelően az up (fel) és down (le) nevet kapta, a harmadik pedig a strange nevet. Jelölésük ennek megfelelően u, d és s. A kvarkmodell szerint a kvarkok kétféleképpen kapcsolódhatnak össze: három kvark bariont (és három antikvark antibariont), illetve egy kvark és egy antikvark mezont formál. A kvarkok spinje feles
(1. táblázat), tehát fermionok. Három kvark kötött állapota is fermion lesz tehát, míg a kvark+antikvark rendszer bozon. A kvarkok töltése
+2/3 és -1/3, így adja ki például a p = (uud) állapot a proton pozitív és az n = (udd) a neutron zérus töltését. Az izospin harmadik komponense tehát az u- és d-kvark töltésével van szoros összefüggésben, egységnyi növelése ugyanis azt jelenti, hogy az adott részecskében egy d-kvarkot u-kvarkra cserélünk, tehát a töltését egységgel növeljük: + 2/3 - (-1/3 ) = 1.
A barionokhoz bariontöltést rendelünk, amely barionokra +1, antibarionokra -1, más részecskékre pedig zérus. Ennek megfelelően a kvarkok bariontöltése 1/3 (az antikvarkoké -1/3 ); a bariontöltés a reakciók során mindig megmarad, hiszen fermionokról van szó.
A kvarkok színe
A kvarkmodell, habár sikeresen megmagyarázta az összes megfigyelt részecske tulajdonságait, azonnal komoly ellentmondásokba keveredett. Nem volt érthető például, miért csak a fenti két állapot jöhet létre belőlük, miért nincsenek szabad kvarkok, és hogyan lehetnek egy barionban azonos fizikai állapotú kvarkok, holott a Pauli-elv ezt fermionokra határozottan tiltja. A részecskefizika fejlődése során, ha valami érthetetlennel találkoztunk, gyakran bevezettünk egy új kvantumszámot. Ez történt most is: mivel három lehetséges állapotot kellett leírnunk, a színlátás három alapszínének analógiájára az új kvantumszámot színnek hívjuk.
A kvarkok három színének bevezetése az erős kölcsönhatás töltéseként az összes fenti problémát egyszeriben megoldotta. Az újabb kvantumszám feloldotta a Pauli-tiltást, és annak posztulálása, hogy a természetben csak fehér (azaz a három színt meghatározott módon tartalmazó) részecskék létezhetnek - mert a szín-szín vonzás annál erősebb, minél inkább távolodnak egymástól a színek hordozói -, megmagyarázta, miért csak a 3-kvark és kvark+antikvark állapotok megengedettek. Egyedül ezek fehérek ugyanis a lehetséges kombinációk közül.
A három fermioncsalád
A kvarkmodelltől a részecskefizika Standard Modellje felé az egyik legnagyobb lépést Glashow, Iliopoulos és Maiani (az utóbbi jelenleg éppen a CERN főigazgatója) tették 1970-ben a róluk elnevezett GIM-mechanizmus bevezetésével. Különböző kísérleti megfigyeléseken alapuló elméleti megfontolások alapján kimondták, hogy a kvarkok párokban léteznek. A három addig ismert kvark mellett tehát léteznie kell egy negyediknek, az u-kvarkhoz hasonlóan +2/3 töltéssel. A negyedik, c- (charm) kvarkot 1974-ben sikerült két csoportnak is kísérletileg megfigyelnie (az újonnan megfigyelt c 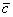 kötött állapotot a két csoport különbözőképpen jelölte, ezért máig
J/
kötött állapotot a két csoport különbözőképpen jelölte, ezért máig
J/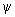 részecskének hívjuk). Ezért Richter és Ting 1976-ban megkapták a fizikai Nobel-díjat.
részecskének hívjuk). Ezért Richter és Ting 1976-ban megkapták a fizikai Nobel-díjat.
A párokba rendeződött kvarkok mellett ugyanannyi leptonpárnak kell lennie, különben elromlik az elmélet belső rendje, anomáliák lépnek fel, amikor a részecskereakciók valószínűségét számítjuk. Az anomáliák kiküszöbölése megköveteli, hogy a leptonok és kvarkok összes töltése zérus legyen, és a kvarkok háromféle színével ez a feltétel családonként teljesül: 0 -1 + 3  (⅔ - ⅓ ) = 0. Amikor tehát Perl csoportja 1975-ben felfedezett egy harmadik leptont, a
(⅔ - ⅓ ) = 0. Amikor tehát Perl csoportja 1975-ben felfedezett egy harmadik leptont, a 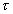 -t (Nobel-díj, 1995; ami késik, nem múlik), azonnal feltételezték egy újabb kvarkpár létezését. Így alakult ki az
1. táblázat menazsériája; azóta mindkét új kvarkot megfigyelték. A fermionok helyét a párokban a nukleonok izospinjének mintájára bevezetett gyenge izospin (T) jelzi: a felső részecskékre a gyenge izospin harmadik komponense T3 = + 1/2 , az alsókra T3 = - 1/2. A párok gyenge-izospin dublettek.
-t (Nobel-díj, 1995; ami késik, nem múlik), azonnal feltételezték egy újabb kvarkpár létezését. Így alakult ki az
1. táblázat menazsériája; azóta mindkét új kvarkot megfigyelték. A fermionok helyét a párokban a nukleonok izospinjének mintájára bevezetett gyenge izospin (T) jelzi: a felső részecskékre a gyenge izospin harmadik komponense T3 = + 1/2 , az alsókra T3 = - 1/2. A párok gyenge-izospin dublettek.
Ezen a ponton joggal vetődik fel a kérdés, vajon hány hasonló kvark-lepton-családot rejteget még a Természet. A választ a CERN és Stanford nagyenergiájú e- e+ ütközőnyalábjai4 adták meg csaknem tíz éve: semennyi, csak három család létezik. A fenti gyorsítókon előállított Z-bozon ugyanis sokféleképpen elbomolhat, és a Standard Modell valamennyi bomlási csatornát pontosan leírja; az egyetlen ismeretlen tényező a neutrínók száma. Mivel a hagyományos detektorok a neutrínót nem észlelik, ezek láthatatlan bomlási módusok. A teljes bomlási élettartam és a látható módusok mérésével megállapították a láthatatlanokét, és abból kiderült, hogy háromféle könnyű neutrínó, tehát csak a már meglevő három leptoncsalád létezik (egy esetleges nehezebb, tehát a töltött leptonokéval vagy a mezonokéval összemérhető tömegű neutrínóhoz nem okvetlenül tartozna új család).
Az 1. táblázat tehát a Standard Modell által jelenlegi tudásunk szerint megengedett, összes alapvető fermiont tartalmazza. Az olvasót ne rémítse meg a fenti kijelentés látszólag túlzott óvatossága. A Standard Modellt sokféle módon sikerült elméletileg kiterjeszteni, ami számos (sót időnként rengeteg) új, hipotetikus (azaz egyelőre csak a fizikusok képzeletében élő) részecske megjelenéséhez vezetett. Bár semmiféle kísérleti bizonyítékot nem találtunk sem a Standard Modell teljeskörű érvénye ellen, sem a kiterjesztések jósolta új jelenségek, illetve részecskék mellett, az utóbbiakat teljesen kizárni sem lehet.
A kölcsönhatások
Mint említettük, a gravitációról elfeledkezve, a részecskefizikában három kölcsönhatásról szoktunk beszélni, alapvető tulajdonságaikat a 2. táblázatban összegezzük.
A Standard Modell szerint a kölcsönhatások helyi szimmetriákból erednek, forrásuk valamilyen töltés, és bozonok közvetítik őket. Ezek a bozonok nemcsak a kölcsönhatások hordozóiként, hanem önállóan is léteznek, ugyanolyan elemi részecskék tehát, mint az 1. táblázat fermionjai, és kísérletileg is észlelhetők. Egy fermion részt vesz egy kölcsönhatásban, ha rendelkezik annak töltésével: a gyenge kölcsönhatás valamennyi feimionra hat, az elektromágneses az elektromosan töltöttekre vagy mágneses momentummal rendelkezőkre, az erős pedig a színes kvarkokra.
Az elektromágneses kölcsönhatás hordozója a foton (jele
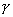 ), a gyengéé a három gyenge bozon (W+, W- és Z0).
Az erős kölcsönhatás során a két kvark színt cserél, hordozójának, a gluonnak (glue angolul ragasztó) egy színt és egy antiszínt kell hordoznia. Ez nyolc különböző gluont jelent, mert a 3
), a gyengéé a három gyenge bozon (W+, W- és Z0).
Az erős kölcsönhatás során a két kvark színt cserél, hordozójának, a gluonnak (glue angolul ragasztó) egy színt és egy antiszínt kell hordoznia. Ez nyolc különböző gluont jelent, mert a 3  3 lehetséges szín-antiszín kombinációból létrehozható egy olyan
3 lehetséges szín-antiszín kombinációból létrehozható egy olyan
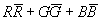 , amely fehérből fehérbe vinne át, tehát nem jelentene színcserét.
, amely fehérből fehérbe vinne át, tehát nem jelentene színcserét.
Az elektromágneses és a gyenge kölcsönhatás összehasonlítására kitűnő példa a pionbomlás. Tipikus elektromágneses folyamat a semleges pion bomlása
két fotonra: 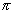 0
0 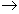
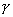
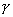 , 8
, 8  10-17 s élettartammal. A negatív pion ugyanakkor csak gyenge kölcsönhatásban tud bomlani müonra és antineutrínóra,
10-17 s élettartammal. A negatív pion ugyanakkor csak gyenge kölcsönhatásban tud bomlani müonra és antineutrínóra,
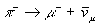 , és az élettartama ennek megfelelően 26 ns = 2,6
, és az élettartama ennek megfelelően 26 ns = 2,6  10-8 s, nyolc nagyságrenddel nagyobb a semleges pionénál: Vegyük észre, hogy az utóbbi reakcióban a bozon eltűnt, de a lepton egy antilepton társaságában keletkezett: a fermionok száma megmarad, a bozonoké nem.
10-8 s, nyolc nagyságrenddel nagyobb a semleges pionénál: Vegyük észre, hogy az utóbbi reakcióban a bozon eltűnt, de a lepton egy antilepton társaságában keletkezett: a fermionok száma megmarad, a bozonoké nem.
Az elektromágneses kölcsönhatás tulajdonságait régen ismerjük: forrása az elektromos töltés, közvetítő bozonja a foton, helyi szimmetriája, amelyből származtatható, a Maxwell-egyenletek mértékszimmetriája.5 Ez a szimmetria az elektromágneses potenciál nullpontjának szabad választásával kapcsolatos: a fizikai erő potenciálkülönbség következménye, ezt például a madarak bizonyítják, amikor nyugodtan üldögélnek a nagyfeszültségű vezetéken. Mint említettük, globális érvénye eredményezi a töltésmegmaradást. Az elektromágneses kölcsönhatást úgy származtatjuk, hogy a szabad fermiont leíró Dirac-egyenlettől megköveteljük, hogy helyről helyre változó mértéktranszformációval szemben legyen invariáns; ettől fellép egy vektortér, amelyet könnyű6 az elektromágneses vektorpotenciállal azonosítani.
Mivel a foton tömege zérus, az elektromágneses kölcsönhatás végtelen hatótávolságú; potenciálja a töltések távolságával fordítottan arányos. A fotonokat mindennapi életünk során szemünkkel és televíziós vevőkészülékünkkel is észleljük, létezésükhöz tehát nem férhet kétség.
Az erős kölcsönhatás forrása a színtöltés, közvetítője a nyolc gluon, helyi szimmetriája pedig a három színnek megfelelően az SU(3) szimmetria.7 A gluonok tömege is zérus, tehát az erős kölcsönhatás is végtelen hatótávolságú, potenciálja viszont közelítőleg a színes részecskék távolságával egyenesen arányos. Ez annak a következménye, hogy - a fotonnal ellentétben - a gluonok maguk is hordozzák a színt, a kölcsönhatás forrását, tehát saját magukkal is kölcsönhatnak. Ha tehát két kvarkot megpróbálunk egymástól elválasztani, a terük energiája a távolsággal nő, mert a gluonok egyre több újabb gluont és kvarkantikvark-párokat keltenek közöttük, a kvarkok pedig hadronokká alakulnak, amíg az összes szín el nem tűnik; ezért nem észlelünk szabad kvarkot (kvarkbezárás).
A kvarkokat mégis észleljük kísérletileg, nagyenergiájú részecskeütközések során keletkező, közel egy irányba kirepülő részecskenyalábok, hadronzáporok formájában. Elektron-pozitron ütközésnél például keletkezhetnek kvark-antikvark-párok; és a megmaradási törvények miatt - tömegközépponti rendszerben - ezeknek 180° alatt kell kirepülniük. Ahogy egymástól távolodnak, az állandóan növekvő térerő addig kelt gluonokat és újabb kvark-antikvark-párokat, amíg valamennyi részecske színtelen nem lesz. Nagyobb energiákon ez akkora részecskesokaságot jelent (10-20 részecskét egy záporban), amely semmilyen más fizikai folyamattal nem értelmezhető. A gluonok létezését a 3-hadronzáporos események észlelése bizonyította. Ezek ugyanis esak úgy jöhetnek létre, ha egy kvark-antikvark-pár egyik tagja kibocsát egy gluont, minden más hasonló folyamatot tiltanak a megmaradási törvények.
A kvarkbezárás következményeként az erős kölcsönhatás hatótávolsága gyakorlatilag igencsak véges; mintegy 1 fm, azaz 10-15 m, az atommag méretéhez közeli. Az atommagot tehát az erős kölcsönhatásnak a nukleonokból kilógó része tartja össze, hasonlóan a kémiai kötéshez, amely a semleges atomokból kilógó elektromágneses potenciál következménye.
A gyenge kölcsönhatás furcsaságai
A gyenge kölcsönhatás származtatására a gyenge izospin SU(2) szimmetriája szinte tálcán kínálja magát. A dolog azonban ennél sokkal érdekesebb: az elmélet a három közvetítő részecske, a W+, W- és Z0 gyenge bozonok tömegére is zérus tömeget jósol, noha a gyenge kölcsönhatás igen rövid hatótávolságából nagy tömegek következnek. A Heisenberg-féle határozatlansági reláció ugyanis - mint korábban említettük - lehetővé teszi, hogy egy M tömegű részecske 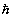 /(Mc2) ideig sértse az energiamegmaradást (itt
/(Mc2) ideig sértse az energiamegmaradást (itt 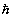 = h/2
= h/2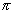 a Planck-állandó és c a fénysebesség vákuumban); így képes a 80 GeV tömegű W+-bozon közvetíteni a neutronbomlásnál,
n
a Planck-állandó és c a fénysebesség vákuumban); így képes a 80 GeV tömegű W+-bozon közvetíteni a neutronbomlásnál,
n 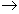 p + e-
+
p + e-
+ 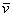 e, felszabaduló 1,3 MeV (csaknem 5 nagyságrenddel kevesebb!) energiát. A gyenge kölcsönhatás hatótávolsága R =
e, felszabaduló 1,3 MeV (csaknem 5 nagyságrenddel kevesebb!) energiát. A gyenge kölcsönhatás hatótávolsága R = 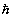 /(MW c)
/(MW c) 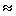 2
2  10-3 fm, közel 3 nagyságrenddel kisebb, mint az atommag átmérője.
10-3 fm, közel 3 nagyságrenddel kisebb, mint az atommag átmérője.
Ezt az ellentmondást oldotta fel a spontán szimmetriasértés elmélete (felfedezőjéről Higgs-mechanizmusnak hívjuk), amely a Standard Modellt mai formájára hozta. A Higgs-mechanizmus feltételezi egy olyan négykomponensű függvény (komplex izospin-dublett) létezését, amely hozzáadódik a fermionokat leíró függvényhez, mintha a fermionok ebben a térben mozognának. Az egyébként tömeg nélküli fermionok a Higgs-térrel kölcsönhatásban tömeget nyernek, hasonlóan ahhoz, ahogy egy töltött részecske folyadékban sokkal nehezebben mozog, mint vákuumban, mert az elektrosztatikus vonzás következtében magával kell hurcolnia a környezetében levő, polarizált molekulákat.
A Higgs-tér sérti az SU(2)-szimmetriát, és ezzel - a szilárdtestfizika kvázirészecskéihez hasonlóan - olyan új részecskéket hoz létre, amelyek közül három az elmélet zérus tömegű közvetítőrészecskéinek tömeget teremt, létrehozva a három áhított, nehéz gyenge bozont. A negyedik komponense pedig, melléktermékként, újabb nehéz részecskét hoz létre, a Higgs-bozont. A Higgs-mechanizmusnak még számos jótékony hatása van, amely teljesen kezelhetővé teszi az addig ellentmondásokkal terhes modellt: lehetőséget teremt arra, hogy kiszámoljuk a folyamatok valószínűségeit. Nélküle az egyenletekben végtelen tagok lépnek fel, a hatására azonban kölcsönösen kiejtik egymást.
Adósok vagyunk még az 1. táblázatban szereplő két jel, az L index és a kvarkok jele melletti aposztróf magyarázatával: mindkettő a gyenge kölcsönhatás különlegessége.
Az egyik a paritássértés. Ha egy karórát úgy építünk meg, hogy a tervrajzát tükörben nézzük, azaz tükrözzük, valószínűleg pontosan jár majd, legfeljebb a mutatója forog majd ellenkező irányban és a számai-betűi lesznek az általunk megszokottak tükörképei. Sokáig azt hittük, hogy a fizika valamennyi törvénye tükörszimmetrikus, amíg C.S. Wu asszony kísérlete meg nem mutatta, hogy mágneses térben a kobalt atommag gyenge bomlása során a térrel ellenkező irányban bocsátja ki bomlási elektronjait.
A másik két kölcsönhatás megőrzi a rendszerek paritását, azaz emlékszik rá, jobbra vagy balra (azaz a mozgás irányban vagy azzal ellenkezőleg) volt-e polarizálva, míg a gyenge maximálisan sérti azt. Ez abban nyilvánul meg, hogy a gyenge kölcsönhatás során a részecskék inkább balra, az antirészecskék pedig jobbra polarizálva keletkeznek, amennyire azt a megmaradási törvények engedik: ezt jelképezi az 1. táblázat dublettjei melletti L (angolul left = bal). A neutrínó esete extrém: ha zérus a tömege, a neutrínó csak balra polarizálva, az antineutrínó pedig csak jobbra polarizálva létezhet. Az elmélet természetesen tartalmazza a nemzérus tömegű fermionok jobbkezes változatát is, izospin-szingulettként.
A paritássértés felfedezése után sokáig azt hitték, hogy a CP-szimmetria, tehát a fizikai törvények változatlansága a töltés és paritás egyidejű tükrözésével szemben, általános érvényű; egészen 1964-ig, amikor Cronin és Fitch (Nobel-díj, 1980) felfedezték, hogy a gyenge kölcsönhatás azt is sérti, ha nem is maximálisan, mint a paritást, csak egy icipicit. Mint említettük, a CPT-szimmetriát abszolútnak tartjuk. A CP-sértés elvi lehetőséget nyújt arra, hogy megkülönböztessük a világot az antivilágtól, és valószínűleg kapcsolatban van az anyag-antianyag aszimmetriával. Visszatérve a karóra példájára, a térbeli (P) tükrözés a jobb-bal cserét jelenti, a töltéstükrözés (C) azt, hogy az órát antianyagból csináljuk, az időtükrözés (T) pedig azt, mintha az óramutató mozgását rögzítő videofelvételt ellenkező irányban játszanánk le.
A gyenge kölcsönhatás a kvarkok fajtáját sem tiszteli, ellentétben a másik kettővel: az erős kölcsönhatásban keletkezett kvarkok a gyenge kölcsönhatás szempontjából a három családból vett állapotok keverékei.8 Praktikus szempontból elég vagy az alsó, vagy a felső típusú kvarkokat keverteknek feltételeznünk; megállapodás szerint az alsókat keverjük, és erre utal az alsó kvarkok jelei feletti vessző. Ha a neutrínóknak tényleg nullától különböző a nyugalmi tömege, amire mutatnak kísérleti jelek, akkor a leptonállapotok is keveredhetnek.
A részecskeállapotok keveredését keveredési szögekkel jellemezzük. A három alsó kvarkot egy háromdimenziós tér koordinátatengelyeinek képzelve, a rendszert három szöggel kell elforgatnunk a három tengely körül, hogy megkapjuk az összes lehetséges kvarkkeveredést. A három szögből pedig megkapjuk a (d,s,b) vektort (d',s',b')-be transzformáló Cabibbo-Kobayashi-Maskawa-mátrixot. A CP-sértés a három keveredési szög mellett negyedik paraméterként egy fázisszöget visz a CKM-mátrixba.
Másik nevezetes keveredés a gyenge és elektromágneses kölcsönhatás egyesítésekor (Glashow, Weinberg és Salam: Nobel-díj, 1979) fellépő gyenge keveredés. A részecskefizikában, ha két állapot keveredését nem tiltja valamilyen törvény, akkor keverednek, azaz a természetben előforduló állapotok a kiindulók lineáris kombinációi lesznek. Ez történik a gyenge kölcsönhatás semleges árama és az ugyancsak semleges elektromágneses áram között. Az utóbbi semlegessége viccesen hangzik, hiszen az elektromos áram elektromos töltések árama, viszont mint áram semleges, mert a foton nem hordoz töltést, tehát a kölcsönhatás folyamán a rendszer töltésállapota nem változik meg. A foton és a semleges gyenge bozon keveredésekor csak egy szög lép fel, a Weinberg-szög (vagy weak = gyenge keveredési szög), amelyet így
két okunk is van
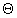 W-vel jelölni.9 A gyenge keveredés miatt lesz a gyenge bozonok tömege különböző: a Z0 valamivel nehezebb a W
W-vel jelölni.9 A gyenge keveredés miatt lesz a gyenge bozonok tömege különböző: a Z0 valamivel nehezebb a W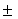 -nál, mert a foton besegít.
-nál, mert a foton besegít.
Valamennyi keveredési szög szabad paraméter, tehát nem elméletileg megjósolható, hanem kísérletileg megállapítandó érték.
A Standard Modell jelene és kilátásai
A Standard Modell alapvető alkatrészei tehát a kétszer három fermioncsalád és a három helyi szimmetria, amelyből a három kölcsönhatás és 1 + 3 + 8 közvetítő bozonja származtatható a szimmetriasértő Higgs-tér áldásos közreműködésével, amely utóbbi melléktermékeként megjelenik a Higgs-bozon.
Nem tudjuk, miért éppen az említett három szimmetria hozza létre a három kölcsönhatást, de azt igen, hogy az elektromágneses kölcsönhatás U(1) szimmetriája az elektromos töltés skalár (azaz egykomponensű) voltával, a gyenge kölcsönhatás SU(2) szimmetriája a kétkomponensű gyenge izospinével, az erős kölcsönhatás SU(3) szimmetriája pedig a háromféle színével van összefüggésben.
A Standard Modell helyességét számtalan kísérleti megfigyelés igazolja. Mindjárt megszületésekor számszerűen megjósolta a gyenge bozonok tömegét és más tulajdonságait, amit a kísérlet később teljes mértékben igazolt (C. Rubbia és társai, Nobel-díj, 1984). A létrehozása óta eltelt csaknem 30 év alatt a kísérlet minden jóslatát teljes mértékben igazolta, semmiféle olyan megfigyelésünk nincs, amely ellentmondana neki. A Higgs-bozon kivételével valamennyi alkatrészét megfigyeltük, utoljára a t-kvarkot, és a Természet vakon engedelmeskedni látszik neki. Még az az új megfigyelés sem mond igazán ellent a Standard Modellnek, hogy a neutrínóknak lehet némi (igen kicsi) tömege.
Joggal merül fel tehát a kérdés, mi szükség van még gyorsítókra, és egyáltalán részecskefizikusokra, ha egyszer ilyen, mindent helyesen leíró elmélettel rendelkezünk. A válasz a Standard Modell nevében rejlik: nem teljes elmélet, csak modell, amelyről nem igazán értjük, miért működik ilyen jól. Három remek elméletet, a három kölcsönhatásét, jónéhány szabad paraméterrel ellátva összeházasítottunk; megfejeltük egy ad hoc Higgs-mechanizmussal, mert különben nem működik; mesterségesen hozzátettük a fermionok tömegét, és annak örülünk, hogy mindezt hagyja, azaz nem vezet elméleti ellentmondásokra. Nem sikerült még észlelnünk a modell kulcsfiguráját, a Higgs-bozont, amelynek léte és tulajdonságai bizonyítanák a Standard Modell érvényét.
Vannak jelei annak, hogy a Standard Modell mögött egységes, mélyebb elmélet lehet. Erre vall az a megfigyelés, hogy a három kölcsönhatás erőssége, azaz csatolási állandója az energia növelésével hasonló érték felé tart, tehát mintha egy univerzális kölcsönhatásra lennének visszavezethetők. Az elmúlt 3 évtizedben a Standard Modellnek számos kiterjesztése született, és a jövő kísérleteinek kell döntenie, melyik írja le közülük helyesen a mikrovilágot. Közülük ma a szuperszimmetria (SUSY) a legnépszerűbb, bár igazát egyelőre semmiféle kísérleti megfigyelés nem bizonyítja. Szimmetriát feltételez a fermionok és bozonok között, tehát azt, hogy minden ismert fermionnak és bozonnak van szuperszimmetrikus partnere: a feles spinű leptonoknak és kvarkoknak zérus spinű szleptonok (szelektron, szmüon, sztau és szneutrínóik) és szkvarkok, a kölcsönhatásokat közvetítő, egyes spinű bozonok (foton, W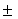 , Z0 és a 8 gluon) szuperpartnerei a feles spinű fotínó, wínó, zínó és a gluínók, a zérus spinű Higgsbozoné pedig az ugyancsak feles spinű higgszínó.
, Z0 és a 8 gluon) szuperpartnerei a feles spinű fotínó, wínó, zínó és a gluínók, a zérus spinű Higgsbozoné pedig az ugyancsak feles spinű higgszínó.
A Standard Modell lehető legegyszerűbb szuperszimmetrikus kiterjesztése, a Minimális Szuperszimmetrikus Standard Modell (MSSM) az elmélet csaknem valamennyi problémáját tetszetősen megoldja, de igen nagy áron: a rengeteg új részecske mellett igen sok új paraméter bevezetésével. Az utóbbi években érdekes versenyfutásnak vagyunk tanúi a kísérleti és elméleti kutatók között: a kísérletiek hiába igyekeznek megfigyelni a megjósolt új szuperpartnereket, és eközben mind nagyobb részeket zárnak ki a lehetséges paraméterértékek terében; eközben az elméletiek, számításaik, modelljeik finomításával egyre növelik az elméleti alapon megengedett és kísérletileg még nem tanulmányozott paramétertartományokat.10
Ajánlott irodalom
SIMONYI KÁROLY: A fizika kultúrtörténete - Gondolat, Budapest, 1986, 5.5.
fejezet
LEON LEDERMAN: Az isteni a-tom, avagy mi a kérdés, ha a válasz a Világegyetem -Typotex, Budapest, 1996 (Fordította: Vassy Zoltán)
KISS DEZSŐ, HORVÁTH ÁKOS, KISS ÁDÁM: Kísérleti atomfizika - ELTE Eötvös Kiadó, Budapest, 1998
Rengeteg közérthető információ található a KFKI honlapján: http://www.kfki.hu/
_______________________
Megjelent a "Nukleáris Tudomány és a 20. század" című MTA kiadványban (Budapest, 2001). A jelen közlés Vértes Attila szerkesztő hozzájárulásával történik.
_______________________
1
A megfelelő szimmetriacsoportaz SU(2) a 2 x 2-es speciális (egységnyi determinánsú) unitér (U' U=1, a mátrix transzponált-konjugáltja egyenlő az inverzével) komplex mátrixok csoportja. Ha a szabadsági fokok számát növeljük, hasonló tulajdonságú, magasabb szimmetriacsoportokat kapunk, az SU(3) elő is fordul majd a későbbiekben.2
Az Einstein-féle tömegformula, E = mc2, értelmében a részecskék tömegét energiával fejezzük ki. 1 eV az a mozgási energia, amelyet egységnyi töltésű részecske 1 V potenciálkülönbség átszelése során szerez; nagyobb egységei a MeV = 106 eV és a GeV = 109eV.3
Kvantumszám: a mikrovilág olyan fizikai jellemzője, amely csak bizonyos meghatározott adagokkal kvantumokkal változhat; ilyen például az elektromos töltés és az impulzusmomentum.4
A hagyományos gyorsítók részecskenyalábja álló céltárgyba ütközik, így hoz létre új részecskéket. Sokkal tisztább körülmények között, sokkal nagyobb energiákat lehet elérni, ha két részecskenyalábot gyorsítanak egymással szemben, és egy észlelőrendszer közepén ütköztetik.5
Az unitér (U'U= 1) 1 x 1-es mátrixok (azaz komplex számok) U(1) szimmetriacsoportja.6
Főleg, ha nagyon akarjuk.7
3 x 3-as speciális (egységnyi determinánsú) unitér mátrixok szimmetriacsoportja.8
Precízebben fogalmazva: a kvarkok erős kölcsönhatás szerinti saját állapotai nem egyeznek a gyenge szerintiekkel.9
A részecskefizikusok kedvenc görög betűje a szi.gif igyekszünk minden szöget azzal jelölni.10
Ebből a megfogalmazásból az olvasó számára nyilvánvalóvá kell válnia, hogy a szerző maga kísérleti kutató.