A LEVEGŐSZENNYEZŐDÉS SZÁRAZ KIHULLÁSÁNAK FIZIKAI MODELLEZÉSE

Márki-Zay János
Vásárhelyi Cseresnyés Kollégiumok
Hódmezővásárhely

A környezetvédelmi ismeretek tanítása, fontosságánál fogva, az iskolai képzés nem elhagyható része, ugyanakkor még hiányosak a jelenségek megértését szemléltető módszerek. A mai kor egyik legnagyobb környezeti ártalmát jelentő levegőszennyeződések, az aeroszolok többsége rendkívül kicsiny, szabad szemmel nem látható részecskékből áll. Az ilyen apró részecskékre a térfogatukhoz mérten viszonylag igen nagy felület a jellemző. Ez adta az ötletet, hogy a hétköznapi életben gyakran használt, de látható méretű, ugyancsak viszonylag nagy felületű papírlappal kíséreljem meg a modellezésüket. A hasonlóság több vonatkozásban is szembeötlő. A modellezés érdekes paradoxona, hogy modellezéshez használt papír felületét csökkentve, egyre nagyobb porszemcsét modellezhetek. Az alapvető modellkísérlet mellett megemlítek néhány további kísérletet is, amelyekkel az aeroszolok környezetvédelmi szerepét fokozottabban megismerhetjük.

A modellkísérlet leírására egészében jellemző az integráló megközelítés, bár tanári szakomnak megfelelően, elsősorban a matematikai (testesség) és a fizikai vonatkozásokat (ülepedési sebesség, a tehetetlenségi és a viszkózus erők aránya, Brown-féle hőmozgás, elektrosztatikai feltöltődés, fényelnyelés stb.) emeltem ki, de felhívom a figyelmet néhány fontos kémiai vonatkozásra is (gyúlékonyság, szubsztitúciós reakció). A matematika és fizika tanításához kapcsolható analógiákon kívül az aeroszolok biológiai és kémiai vonatkozásban is érdeklődésre tarthatnak számot.

A leírt modellkísérlet egyszerűségénél fogva emberközelbe hozza a mai tudományban és az oktatásban is egyre nagyobb jelentőségű modellmódszert mint a valóság megismerésének és megértésének korszerű és nélkülözhetetlen eszközét.

Jelen cikkből kiderül, hogy a levegőszennyeződések témájának középiskolai szakköri feldolgozása során magam is kipróbáltam a modellt. A kísérletek és a hozzájuk tartozó mérések és grafikonok elkészítésébe, az eredmények kiértékelésébe a szakkör tagjait is bevontam. A szakköri feldolgozás során igen kedvező tapasztalatokra tettem szert. Sikerült a tanulók érdeklődését felkeltenem a környezetvédelem fontosságával kapcsolatban, és megértetnem a levegőszennyeződések szerepét életünkben. A tanulók bevonása arra is lehetőséget ad, hogy jártasságra tegyenek szert a kísérletezésben és a kísérlethez szükséges mérések elvégzésében. Másrészt, mint könnyen és gyorsan bemutatható kvalitatív kísérlet, nemcsak a tanári szemléltetést segítheti, hanem - akár házi feladatként - lehetőséget ad a tanulók otthoni kísérletezésére és tapasztalatok levonására.

Az alábbiakban részletezett modellező eljárást saját ötlet alapján dolgoztam ki a savasodásért nagyobb mértékben felelős száraz ülepedésre vonatkoztatva, de a modell a hasonlóság miatt a nedves ülepedésre is tartalmaz hasznosítható elemeket. A száraz ülepedés következtében az élővizek aszályos időjárási viszonyok közepette is savasodhatnak. A savasodás vizsgálata során nem is lehet tökéletesen elkülöníteni a folyton eső száraz csapadékot és a csapadék nedves formáját. Maga a kísérlet kvantitatív formában igen röviden bemutatható, de úgy érzem, szükséges részletesebben is leírnom.

Számomra a levegőben lebegő részecskék egyik legfontosabb tulajdonságának az látszott, hogy kicsiny méretük miatt roppant nagy a relatív felületük, azaz rendkívül kicsiny a testességük.¹ Ez adta az ötletet, hogy a láthatóság határa alá eső aeroszol egyes részecskéit látható, de ugyancsak kicsiny testességű, azaz térfogatukhoz képest nagy felülettel rendelkező papírlapokkal modellezzük. (Gondolva a matematika és a fizika iránt mélyebb érdeklődést mutató olvasókra és a szaktanárokra a modell egyszerűsége ellenére sem mellőztük a matematikai és a fizikai összefüggéseket, a mérési eredményeket és a grafikonokat.)

A kísérletekhez - amelyeket részben szakköri foglalkozáson a tanulókkal együtt végeztünk - közönséges írólapokat használtunk. Így a modellezés nemcsak rendkívül egyszerűnek, de nagyon olcsónak is bizonyult.

Az ejtési kísérleteim során használt 14,5 cm széles, 20,8 cm hosszú (A/5-ös méretű) és 0,008 cm vastag papírlap felülete (praktikusan csak az alap kétszeresét számítva): 0,06032 m², térfogata pedig 2,4128 10^-6 m³.

Így a felület/térfogat arány 25000 m^-1, a testességük pedig 0,00004 m (4 10^-5 m). Az alkalmazott modell és a valóságos aeroszol testességének jelentős eltérése miatt a modellkísérletek elvégzését követően nagy várakozással tekintettem a mért eredményekre. Könnyen kiszámítható, hogy testessége alapján a papírlap egy 1,2 10^-4 m sugarú aeroszol gömböt, azaz óriás részecskét modellez, amely a valódi aeroszol részecskék testességét átlagosan több nagyságrenddel is meghaladja, akkor is, h a az aeroszolok alakját önkényesen gömbnek tekintem (azaz adott térfogat mellett maximális testességűnek):

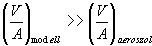
A levegőben lebegő aeroszol részecskéket ugyanis méreteik alapján három csoportba szokás sorolni:

1. Aitken (éjtkën)-féle részecskék: ha a gömb alakúnak tekintett részecske sugara kisebb, mint 0,1 mikron. Felület/térfogat arányuk 30000000 m^-1, testességük pedig 3,33 10^-8 m.
2. Nagy részecskék: ha a sugár 0,1 és 1 mikron közé esik. Felület/térfogat arányuk hárommillió m^-1 és harmincmillió m^-1 közé, testességük pedig 3,33 10^-8 m és 3,33 10^-7 m közé esik.
3. Óriás részecskék: ha a sugár nagyobb 1 mikronnál. Felület/térfogat arányuk kisebb, mint 3000000 m^-1. Testességük nagyobb, mint 3,33 10^-7 m.

A modellezés matematikai szempontjait megvilágítva, egyértelmű, hogy matematikaóráinkon elsősorban a testmértannal való ismerkedés során érinthetjük a térfogat és felület arányának jelentőségét, megemlítve, hogy az egyenlő térfogatú testek között a gömbnek a legkisebb a felszíne. Itt szót ejthetünk az első közelítésben gömbszerűnek tekintett aeroszolokról, amivel összefüggésben felszín- és térfogatszámítási feladatokat végeztethetünk tanulóinkkal. A hasonló testek (például aeroszolok) felszínének és térfogatának arányával kapcsolatban kitűzött feladatok haszonnal illeszthetők a tananyagba is. Érdemes már itt is megemlíteni, hogy a matematikai hasonlóság (az edtérő testesség következtéhen) nem jelent egyhen fizikai hasonlóságot is, s ez - mint példák sorával igazolhatjuk - az egyik legnehezebb gondot jelenti a modellalkotásban. Mivel a testességnek, továbbá a vele rokon variációszámítási problémakörbe tartozó problémáknak (mint például az izoperimetria) a gyakorlati jelentősége igen nagy, de a jelenlegi tantervek szerint erről még a középiskolai matematikaórákon is csak érintőlegesen lehet szó (csak szakköri foglalkozás keretében képzelhető el a téma részletesebb tárgyalása az érdeklődő tanulóink számára).

A környezetvédelmi s így például a levegőszennyeződéssel kapcsolatos problémáknak másik természetszerű felhasználási lehetőségét a függvénytan biztosítja. Mind az egyenes arányosságra, mind a fordított arányosságra vonatkozóan találhatunk szemléletes példát. Lehetőségünk van az aeroszolokkal összefüggő függvénykapcsolatok vizsgálatára, illetve ábrázolására. Így például a felszín és térfogat (a testesség) függvény, vagy a v= v(r) függvény ábrázolása (ahol az elmélet szerinti fordított arányosságra jellemző hiperbolát igen jól közelíti a modellkísérletek mérési adatai alapján készített grafikon) stb.

Hidy és Brock nyomán az aeroszolok négy jellemző fizikai tulajdonságát vetem össze a papírmodell tulajdonságaival.

Mivel modellalkotásunk alapjának a testességet fogadtuk el, ezért a fizikai vizsgálódásunk alkalmával tekintettel kell lennünk arra, hogy az aeroszolok ülepedését kiváltó nehézségi erő nem a test térfogatával, hanem tömegével arányos. Ez könnyen áthidalható, ha elfogadjuk egyszerűsítő feltételként, hogy az aeroszolokat homogénnek (azonos sűrűségűnek) tekintjük, s ekkor a testesség is egyenesen arányos a tömeg és felület arányával. További egyszerűsítő feltevést alkalmazva az aeroszol részecskéket egységesen r sugarú gömbnek tekintjük, amelyek belső súrlódással rendelkező (viszkózus) gázban (vagy folyadékban) mozognak v sebességgel. Ekkor a Stokes féle ellenállástörvény értelmében a közeg a részecskére F_e = 6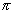vrv nagyságú ellenállást fejt ki. Így a gömb alakúnak tekintett részecske mozgása csak addig lesz gyorsuló, amíg a részecskéket mozgató nehézségi erő a mozgást akadályozó erővel egyensúlyba nem kerül, azaz 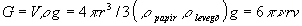ahonnan , ha a részecske sűrűségénél jóval kisebb levegősűrűséget nem vesszük figyelembe . A levegő belső súrlódása 20 °C-on 1,81 10^-4 poise (1 poise = 0,1 kg/ms).

Ha nem vesszük figyelembe a tengerszint feletti magasságot és a légkör konvektív és turbulens mozgásait, akkor a talajhoz közel átlagosan 0,1 m/s sebességgel szokás számolni, ami körülbelül 30 mikron = 3 10^-5 m sugarú részecskére vonatkozik, amelynek testessége:

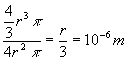
Az írólapokkal végzett modellkísérletek esetében először ejtési kísérletek alapján út-idő grafikont készítettem, ahonnan a sebesség meghatározható. Zárt térben (a zavaró légmozgásokat kiküszöbölve) a papírlapokat rendre 7,5 m, 2 m, 1,5 m és 1 m magasságból leejtve mértem meg az esés idejét. Az ejtési kísérleteket öt különböző felületű, de azonos tömegű papírlappal végeztem el úgy, hogy a papírlapokat rendre a felére, a negyedére, a nyolcadára és végül a tizenhatodára hajtottam össze. A kapott mérési eredményeket átlagoltam. A kísérletsorozat alapján nyilvánvaló, hogy a legnagyobb felületű lapok kihullása történik a leglassabban, amelyek nagyságukkal ellentétben a relatíve nagy felület/térfogat aránynak megfelelően a legapróbb porszemcséket modellezik, míg az egyre jobban összehajtogatott papírlapok egyre nagyobb részecskéket modelleznek a felület/térfogat arány csökkenésének megfelelően. (Testességük alapján a kísérletsorozatban alkalmazott papírlapok rendre 1,2 10^-4 m; 2,4  10^-4 m; 4,8 10^-4 m; 9,6 10^-4 m; 1,92 10^-3 m sugarú gömböknek feleltethetők meg.)

Az ejtési kísérletek során zavaró tényezőként számolni kell azzal, hogy a rendre ismétlődő hajtogatások által, azaz a méretek (a felület) csökkentésével a merevség növekszik. A modellkísérletek során a megadott papírvastagság mellett a légellenállás deformáló hatásának tulajdonítható lényeges, szemmel is érzékelhető alakváltozást csak a még nem összehajtott papírlapok esetében tapasztaltam.

A kísérleti feltételek analóg jellegének megőrzése érdekében - a deformáció mértékének növekedése miatt feltehetően nem érdemes sokkal nagyobb papírlapokkal próbálkozni, bár erre vonatkozó ellenőrző kísérleteket nem végeztem.

Másik oldalról a túlságosan összehajtott papírlapok esetében a felület/térfogat arány nagyon lecsökken, és a papírlap már nem alkalmas az aeroszolok kihullásának modellezésére, hanem egyre inkább a szabadesés törvényének megfelelően esik.

Ha a méretekre vonatkozó alsó és felső határokat figyelembe vesszük, akkor olyan eredmények születnek, amelyek egybeesnek a modellezni kívánt jelenségekre vonatkozó ismereteinkkel. A modellkísérletek mérési eredményei ezt alátámasztották.

Az út-idő grafikon alapján megállapítható, hogy az esési sebesség nagyon hamar eléri a relatív felület/térfogat arányra jellemző mértéket, s ettől kezdve az esési sebesség egyenletesnek tekinthető.

A tehetetlenségi és a viszkózus erők arányát a részecskék úgynevezett Reynolds-féle száma (Re) adja meg. Jelöljük a tehetetlenségi erőt T-vel! T = ma = Vt²/r. A viszkózus (súrlódási) erőt jelöljük S-sel! S = Vv/r². A két erő aránya dimenzió nélküli puszta szám: R_e = T/S = pvr/, ahonnan következik, hogy v r = konstans, ami azzal egyenértékű, hogy a v= v(r) függvény képe hiperbola.

Annak megfelelően, hogy a szemcséket gömbszerűeknek tekintjük, papírlapjainkat - azok vastagságától eltekintve - kétdimenziós gömböknek, azaz köröknek tekinthetjük, amelyek sugara a felület négyzetgyökével arányos. Ez a megfeleltetés azért is elvégezhető, mert a c (lég)ellenállási tényezőt a körlapnál 1-nek véve, értéke a gömbre nézve 0,4, azaz csak egy konstans szorzóban térnek el egymástól. Így a papírlapok esetében is kiszámítható az r sugár hozzávetőleges értéke, és ábrázolható a v = v(r) függvény, ami jó közelítéssel csakugyan hiperbola.

Ha a mérési adatok alapján 7,5 m magasról ejtve a papírlapokat, az utolsó 5,5 m megtételéhez szükséges időt figyelembe véve kiszámítom az átlagsebességeket az egyes köralakra átszámított papírlapokra, akkor az összetartozó sugár és a sebesség értékekre a következő táblázatot kaphatom:

Az adatok alapján elsősorban a II., III. és IV. méretek esetében az r v szorzat megközelítőleg állandó.

Az aeroszolokra ez a tulajdonság igazán akkor teljesül, ha sugaruk kisebb, mint 0,5 mikron. A részecskék sugarának csökkenésével a térfogathoz viszonyított felület nő, s így relatíve nagyobb felület ütközik a levegőmolekulákkal, s ezáltal lesz az aeroszolok hőmozgása is viszonylag nagy. Ha r = 5 10^-2 m, akkor gömbalakra vonatkoztatva a felület/térfogat arány mértékszámát 3/r értéke adja meg, azaz értéke 6 10⁶ m^-1 , vagy másként 6 millió m^-1.

Számításba véve, hogy papírlapunk esetében a felület/térfogat arány csak 25 000 m^-1 volt, így ennek a feltételnek a teljesüléséhez a papírlapot 240-szeresére kellene nagyítanunk. Ez egy 7,219 m² alapterületű, azaz körülbelül 2,246 m x 3,222 m-es lapot jelentene legalább, s ez még csak a legnagyobb részecskének megfelelő legkisebb lap lenne. Természetesen nem célszerű modellünket ilyen mértékben megnövelni.

Nagy koncentrációjú, kicsiny részecskéknél a Brown-féle hőmozgás miatt bekövetkező ütközések a részecskék nagyobb részecskévé való egyesülésével jár (termikus koaguláció). Ez a gyorsan végbemenő folyamat jelentős szerepet játszik a csapadékképződésben is.

Az úgynevezett Aitken-féle részecskék felső határára vonatkoztatva, ha r kisebb, mint 0,1 mikron, akkor a gömbnek tekintett részecskére nézve is a felület/térfogat arány (3/r) 3 10⁷ m^-1 = 30 millió m^-1. Szabálytalan, üreges felszín esetén ennél jóval nagyobb.

Ennek következményeként az egyébként nem tűz-, illetve robbanásveszélyes anyag finom porai könnyen felrobbanhatnak (nagy az oxidációs felület), amit az is elősegíthet, hogy az elektrosztatikus feltöltődés szempontjából is kedvező a nagy felület.

A 30 milliós felület/térfogat arány eléréséhez a változatlanul 0,00008 m vastag papírlapot 12000-szeresre nagyítva kellene elképzelnünk, amely így 15,88 m széles és 22,79 m hosszú lenne, s a teljes felszíne 723,81 m² lenne.

Az írólapokkal is jól demonstrálható, hogy a felület/térfogat aránytól hogyan függ az anyag gyúlékonysága. Tapasztalhatjuk, hogy a papírlapot egyre jobban összehajtogatva, az egyre nehezebben gyullad meg, s ismert, hogy például a könyvek nem is tartoznak a fokozottan tűzveszélyes anyagok sorába.

<>

A mérések alapján elkészített grafikonok szemléletesen igazolják a modell és a valóság analógiáját, és a tanulók számára érthetőbbé tehetik a szennyező anyagok légkörbeli viselkedését. A modellező eljárás jelentős előnyének tartom, hogy a valósággal analóg módon történik a modellezés. Az ilyen modellt nevezik félmodellnek (a “fél” azonban itt egyáltalán nem pejoratív jelző, hiszen azt jelenti, hogy félig már a valóság).

Az átlagtól nagyobb mértékben is eltérő mérési eredmények a jelenség statisztikus szemlélettel való megközelítését indokolják.

További didaktikai és gazdasági előny, hogy a kísérletek elvégzéséhez csak egy papírlapra és egy stopperórára van szükség, ezért bátran ajánlható felhasználásuk tanórákon, tanulókísérletként és szakköri foglalkozásokon. Kvalitatív kísérletként általános iskolás korú tanulók számára is ajánlható. Mivel a téma szoros kapcsolatban van a mindennapi élettel, azért motiváló hatása erős, s kitűnően felhasználható a tanulók aktivizálására. Saját gyakorlatomban szakköri foglalkozáson csoportmunkában mint mérőkísérletet dolgoztam fel az anyagot. Néhány esetben az átlagtól nagyobb mértékben is eltérő mérési eredmény elősegítheti a tanulók statisztikus szemléletének kialakulását.

Elméletileg a lehulló papírlapokra ható légellenállás forgatónyomatékának eredője a papírlapot az esés irányára merőleges helyzetbe hozza. A nem kellően merev papírlapok azonban könnyen deformálódnak, s ez esetben valamely szabad tengelyük mentén forgásba jönnek. Az esetek többségében ez a forgás csak csekély mértékben lassítja az esést.

A természetben néhány termés, így például a juharfa termésének esésekor annak forgása az esés idejének növekedését eredményezi. A juhartermés forgását az idézi elő, hogy a szárnyas termés tömege zömmel a juhartermés magrészében összpontosul, míg a könnyű propellerszárny a magtól, s a sülyponttól viszonylag távolra kiterjed.

Kísérleteimben nyolc méter magas erkélyszintről leejtve csak 16 másodperc alatt ért földet a termés, azaz átlagsebessége csupán 0,5 m/s volt. Ha a propellerszárny kétharmadát letörtem, akkor már 4 s alatt földet ért. Ezekből a kísérletekből kiderül, hogy a juhartermés esésekor a helyzeti energia nagyobb hányada nem a mozgási energiát növeli, hanem forgási energiává alakul. A termés lelassult esése eredményesen szolgálja a juhar elterjesztését. A propellerszárny forgása ugyanúgy fékezi a termés esését, ahogyan a helikoptercsavar forgása lehetővé teszi a gép sima leereszkedését. Az aeroszolok esetében hasonló módon kialakuló forgató hatás fellépte nem elképzelhetetlen ugyan, de semmi esetre sem játszhat fő szerepet a száraz ülepedés sebességének mértékénél.

<>

A kísérletezésre használt zárt térben 7,5 m magasról a tanulók néhány papírrepülőt is útnak indítottak. Tapasztalataink szerint a papírrepülők repülése csak térben, s nem időtartamban nyúlt meg. Természetesen egészen más a helyzet a szabad légtérben, ahol a légáramlatok a papírsárkányokat órák hosszat is a levegőben tarthatják.

A modellkísérletek a levegőben lévő szennyeződések száraz kihullásán túlmenően tanulságosak lehetnek a folyadékokba, elsősorban a vizekbe került vagy hullott szennyeződések ülepedésére vonatkozóan is.

<>

A savasodást okozó levegőszennyeződések mértékének megnövekedését esetenként vizuálisan is észlelni tudjuk, mert a levegőszennyeződés következtében megnövekedő fényelnyelődés frekvenciafüggő. Legkevésbé a vörös sugarak nyelődnek el, majd a narancsszínű, a sárga, a zöld, a kék, s végül a legnagyobb frekvenciájú ibolyaszín sugarak. Ezzel magyarázható a lenyugvó Nap vörös színe, de az is, hogy a szennyezett levegő erős alkony- vagy hajnalpírt eredményez. Másrészt, a poros vagy párás levegőben az égbolt szürkés vagy fehéres színűnek látszik, mert a molekuláknál nagyságrendileg nagyobb méretű porszemek és vízcseppek a napfény minden hullámhosszúságú sugarát szórják.

A nagyvárosok és iparilag szennyezett térségekben alacsony napálláskor tapasztalható, s a távolabbi környezettől látványosan eltérő, jellegzetes fényelnyelődés és fényszórás segít a szennyező források azonosításában.