VI. SZILÁRD LEÓ NUKLEÁRIS TANULMÁNYI VERSENY

Sükösd Csaba
BME Nukleáris Technika Tanszék

2003 tavaszán hatodik alkalommal rendezte meg a Szilárd Leó Tehetséggondozó Alapítvány és az Eötvös Loránd Fizikai Társulat a Szilárd Leó Nukleáris Tanulmányi Versenyt. A versenyt Marx György akadémikus hozta létre 1998-ban a Szilárd-centenárium évében, s azóta is az ő vezetésével történt mind a feladatok előkészítése, mind pedig a verseny lebonyolítása. Sajnos ebben az évben a Versenybizottságnak már Marx György segítsége nélkül kellett végeznie munkáját. A Szilárd Leó Tehetséggondozó Alapítvány és az Eötvös Loránd Fizikai Társulat elnöksége Marx György halála után Sükösd Csabát (BME) bízta meg a Versenybizottság munkájának irányításával. Az új versenybizottság a verseny folytonosságának biztosítását és korábbi színvonalának megőrzését tekintette elsődleges célnak, ezért a tavaly felvetődött, a versenyt továbbfejlesztő ötleteket (nemzetközi kiszélesítés, illetve külön verseny indítása a fiatalabb korosztály számára) későbbre halasztotta.

Ebben az évben 374 középiskolás indult csaknem félszáz iskolából, az eredmények tanúsága szerint jó felkészültséggel. A hagyomány szerint az első forduló (válogató verseny) 10 példáját az iskolákban lehetett megoldani 3 óra alatt. Kijavítás után a tanárok azokat a megoldásokat küldték be az Eötvös Társulatba, ahol a 9-10. osztályos (junior) versenyzők legalább 40%-os, a 11-12. osztályos (szenior) versenyzők legalább 60%-os eredményt értek el. Ezeket ellenőrizve a bírálóbizottság a legjobb 10 junior versenyzőt és a legjobb 20 szenior versenyzőt hívta be a paksi Energetikai Szakközépiskolában tartott döntőre. A versenyeken bármilyen segédeszköz használható volt (mobiltelefon és Internet kivételével).

Megoldás: először a reakcióra gondolt. Mivel a ⁸Be magától szétesik 2 -részecskére, ezért azt remélte, hogy n-besugárzással ki lehet lökni a ⁹Be-t éppen csak stabilizáló többletneutront, s így neutronsokszorozó magreakciót nyerünk.

Megoldás: A fólia -sugárforrás és detektor között halad át, és a sugárzás intenzitásának változása alkalmas a vastagság ellenőrzésére.

b) Egy mezőgazdász tudni akarja, hogy paradicsombokraiba miként szívódik fel a frissen kihintett foszfortrágya. Megoldás: A foszfortartalmú műtrágyát 14,3 napos felezési idejű, -bomló ³²P izotóppal jelölik meg, és a növényekben felhalmozódott izotóp aktvitását és az aktivitás időbeli változását mérik.

c) Egy kutatóorvos csökkenteni akarja a bizonyos területeket megfertőző légyraj nagyságát. (Célzás: a hímnemű legyekre rossz sors vár.) Megoldás: A hímnemű legyeket sugárzással sterilizálják. Ez a megoldás jobb, mintha megölnék őket, mert egy hímnemű légy nagyon sok nőneművel párosodik, de a nőneműek csak egyetlen hímmel. Ezért azoknak a nőnemű legyeknek, amelyek a sterilizált hímekkel párosodtak, nem lesznek utódaik. Ha pedig a befogott hímeket elpusztították volna, akkor a nőstények találtak volna más hímeket, és tovább szaporodtak volna.

d) Egy agysebész a daganat helyét kívánja megállapítani. Megoldás: A szervezetbe valamilyen pozitronbomló anyagot (pl. ¹⁸F-t) tartalmazó cukortartalmú vegyületet (glükózt) juttatunk. A rákos sejtek anyagcseréje gyorsabb, mint az egészségesé, több tápanyagra van szükségük, a glükóz feldúsul bennük. A daganat helyét a pozitron-bomlást követő annihiláció gamma fotonpárjainak detektálásával lehet meghatározni. Az izotóp feldúsulásának a helyét a több irányból detektált fotonpárok által meghatározott egyenesek metszéspontja adja (ez a pozitron-emissziós tomográfia - PET - alapelve).

3. Uránbányászoknál tapasztalták a tüdőrák gyakoribbá válását, ha nem megfelelő a bánya szellőztetése. Hogyan okozhat a radon tüdőrákot, hiszen nemesgáz, és rövid a felezési ideje, tehát belélegezzük, majd kilélegezzük, mint a nitrogént? Megoldás: A radon bomlásából származó leányelemek rövid felezési idejű fémizotópok, ezek kitapadnak a levegőben lévő aeroszolokra, porszemekre. Ezeket belélegezzük, a tüdőben megtapadnak, és többségük a-bomló lévén, az általuk kibocsátott sugárzás a tüdő hólyagocskáinak falát roncsolva rákot okozhat.

4. Egy, a szájhagyomány szerint legalább 100 éve elsüllyedt hajót átkutatva a búvár az egyik kabinban bontatlan whiskysüveget talált, amelyről azonban leázott a címke. Amikor egy laboratóriumban megmérték ennek a whiskynek a tríciumtól származó aktivitáskoncentrációját, azt találták, hogy az mindössze 3%-a az üzletben frissen vásárolt és 7 éves címkével ellátott whisky aktivitáskoncentrációjának. Igazolható-e ezzel, hogy 100 éve süllyedt el a hajó? A trícium felezési ideje 12,3 év. Megoldás: a radioaktív bomlástörvény segítségével egyszerűen meghatározható, hogy a hajó legfeljebb 70 éve lehet víz alatt.

5. Tegyük fel, hogy egy stabilis alumínium atommagot elemi részeiből (protonokból és neutronokból) építünk fel. Mennyi energia szabadul fel? Mekkora lesz a nukleononkénti kötési energia? Az ²⁷Al atom tömege: m_a = 26,9815 u. Megoldás: A kötési energia összesen 33,48 pJ, a nukleononkénti kötési energia 1,24 pJ. A helyes megoldáshoz figyelembe kellett venni, hogy az atomtömegben a 13 db. elektron tömege is benne van.

6. Az ²³⁵U és az ²³⁸U izotópok diffúziós szétválasztásánál, amely a részecskék relatív sebességkülönbségén alapuló eljárás, gáz halmazállapotú UF₆ (urán-hexafluorid) vegyületet használnak.

a) Az ²³⁵U-t vagy az ²³⁸U-t tartalmazó molekulának nagyobb-e a sebessége? Megoldás: a ²³⁵U-t tartalmazó molekulának.

b) Mekkora a sebességek aránya? Megoldás: 1,0043.

7. Megmérték egy múmiából vett minta ¹⁴C-től származó aktivitását. Ebből meg lehetett állapítani, hogy a mintában a ¹⁴C/¹²C arány csak 69,2 százaléka annak, mint amit a mai növényekben mérnek. (A ¹⁴C felezési ideje: 5730 év.)

a) Becsülje meg a múmia korát? Megoldás: a radioaktív bomlástörvény alapján 3044 év.

b) Milyen tényezőkre kell figyelni, amikor a minta mért aktivitásából a ¹⁴C/¹²C arányra akarunk következtetni? Megoldás: ki kell nyerni a minta széntartalmát, minden egyéb összetevőtől mentesen. Ezt legtöbbször égetéssel teszik meg, de még itt is el kell választani a keletkezett CO₂-t a többi égésterméktől.

8. A Paksi Atomerőmű éves trícium-aktivitáskibocsátása 15 TBq, amely a hűtővízzel távozik.

a) Mekkora tömegű trícium kerül ki a környezetbe 1 év alatt az erőműből? (A trícium felezési ideje 12,26 év.) Megoldás: az aktivitásból és a felezési időből a kibocsátott tríciummagok száma meghatározható, s ebből a keresett tömeg: 0,04 g.

b) Átlagosan hány százalékkal növeli ez meg a Duna vizének természetes (1 Bq/liter) trícium-aktivitáskoncentrációját? (Tegyük fel, hogy az összes kibocsátott trícium a Dunába kerül, és a kibocsátás évközben egyenletes. A Duna átlagos vízhozama 2000 m³/s.) Megoldás: az egy év alatt átfolyt víz természetes aktivitása az adatokból egyszerűen kiszámítható, s így megkaphatjuk, hogy az aktivitáskoncentráció körülbelül 24%-kal nő.

Z(protonszám)	N(neutronszám)	Magok száma
páros	páros	141
páratlan	páros	45
páros	páratlan	51
páratlan	páratlan	5

Tegyük fel, hogy a Föld keletkezésekor a különböző urán atommagok is ezen arányoknak megfelelően keletkeztek. Jelenleg a természetes uránban az ²³⁵U aránya 0, 71 %. Az ²³⁵U felezési ideje , a ²³⁸U felezési ideje . Becsülje meg a Föld életkorát ezen ismeretek felhasználásával? Megoldás: Mára az ²³⁵U-ös mennyisége a maradék urán 0,71%-a része, tehát: , azaz N₁ = 0,00715 N₂. A jelenlegi ²³⁵U és ²³⁸U atommagok N₁, illetve N₂ száma a "kezdeti" N₁(0), illetve N₂(0) segítségével a radioaktív bomlástörvény alapján felírható, ezért az arányukra vonatkozóan kapjuk:

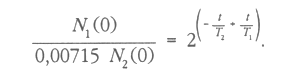
A feladatban megfogalmazott feltételezés szerint N₁(0)/ N₂(0) = 51/141, ezért ebből az egyenletből már csak t ismeretlen, s ez logaritmálással meghatározható: .

10. Ismeretes, hogy nyugalmi tömeggel rendelkező részecske nem érheti el a vákuumbeli fénysebességet. Semmi sem tiltja azonban, hogy egy részecske gyorsabban haladjon egy közegben, mint a fény az adott közegben. Ha ez elektromos töltésű részecskével következik be, érdekes jelenség történik: a fénynél gyorsabban haladó részecske fényt bocsát ki. Ez a Cserenkov-sugárzás. Atomreaktorok hűtővize szép kék színnel világít az aktív zóna közelében a Cserenkov-sugárzás következtében. Ez "térfogati" jellegű sugárzás, nem a fűtőelemek felszíne világít!

a) Milyen részecskéktől származhat ez a sugárzás? Megoldás: Mivel ezt a fajta sugárzást csak elektromos töltésű részecskék válthatják ki, ezért csak elektronok (pozitronok), hasadványok és meglökött atommagok jöhetnek szóba. A Cserenkov-sugárzás kiváltásához nagyon nagy sebességű, s ezért nagy mozgási energiájú részecskék kellenek. Minél nagyobb egy részecske tömege, annál nagyobb a mozgási energiája is, azonos sebesség mellett. A fénysebességhez közeli sebességű elektronok is már elég nagy energiájúak (ld. b) pont), ezért a nehezebb részecskéknek még sokkal nagyobb energiájúaknak kellene lenniük. Ilyen nagy energiájú részecskék jelenlétét kizárhatjuk, ezért az atomreaktorokban nagy sebességű elektronok okozzák a Cserenkov-sugárzást.

b) Legalább mekkora energiájúnak kell lenni ezeknek a részecskéknek ahhoz, hogy a vízben Cserenkov-sugárzást hozzanak létre? Megoldás: Mivel a víz törésmutatója 4/3, ezért a vízben a fény v terjedési sebességére: v² / c² = (3/4)² = 9/16. Tehát az elektronok mozgási energiája (relativisztikus képletet kell használnunk):

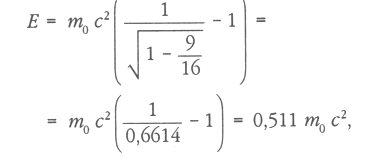
(ahol m₀ az elektron nyugalmi tömege), ezért az elektronnak legalább E= 262 keV energiájúnak kell lennie ahhoz, hogy Cserenkov-sugárzást hozhasson létre.

c) Vajon honnan vannak ilyen energiájú részecskék a reaktorok hűtővizében az aktív zóna közelében? Megoldás: Az első ötlet az, hogy a hasadási termékek bétabomlásakor kilépő elektronok kijutnak a fűtőelemekből, és ezek okoznak Cserenkov-sugárzást a vízben. Ha így lenne, akkor ez a sugárzás csak a fűtőelemek felszíne közelében lenne megfigyelhető, tőle néhány mm-re már nem, hiszen az ilyen energiájú elektronok hatótávolsága vízben körülbelül ekkora. A megfigyelések szerint azonban a Cserenkov-sugárzás "térfogati" jellegű, és nem korlátozódik a fűtőelemek felszínének a közelébe. Ezért a sugárzást létrehozó elektronok nagy részének már a vízben kell keletkezniük! A fűtőelemek erős gamma-sugárzása a vízben Compton-szórással, illetve fotoeffektussal elektronokat lök meg, amelyek így nagy energiára tesznek szert, nagyobbra, mint 262 keV. Mivel a gamma-sugarak hatótávolsága vízben sokkal nagyobb, mint az elektronoké, ezért ez azt is megmagyarázza, hogy miért nem csak a fűtőelemek felületének a közelében figyelhető meg ez a sugárzás.

1. A Paksi Atomerőmű működése óta 2002. december31-ig 240231 GWh energiát termelt. Mennyi oxigént fogyasztottak volna a szénerőművek, ha ezt az energiát szénerőművekkel állítottuk volna elő? (Az energiaátalakítás átlagos hatásfokát vegyük 30%-nak). Megoldás: a szén fűtőértékétől függően 600-700 millió tonna az eredmény.

2. Egy beteg 3,33 MBq aktivitású ¹³¹I injekciót kapott. A ¹³¹I felezési ideje 8,1 nap.

a) 30 nap elteltével mekkora aktivitású izotóp marad a beteg testében, ha az anyagcsere folyamatok 128 nap alatt ürítik ki a jód felét a szervezetből? Megoldás: a jód kiürülése a szervezetből két folyamat, a radioaktív bomlás és az anyagcsere következtében történik. A két folyamat egymástól független, ebből a bomlás lényegében két exponenciális szorzataként írható le. Ennek segítségével a maradék aktivitás kiszámítható: 0,217 MBq.

b) Vajon miért adták be a betegnek ezt a különleges izotópot? Megoldás: Mivel a jód a pajzsmirigyben gyűlik fel, a betegnek valószínűleg valamilyen pajzsmirigybetegsége van.

3. Egy 1 MeV kezdeti energiával keletkezett hasadási neutron grafit-moderátorban bolyong, és sorozatosan ütközik szén atommagokkal. Az egyszerűség kedvéért tegyük fel, hogy a szén atommagok nem mozognak (0 K közelére hűtött grafit), valamint, hogy minden ütközés egyenes ütközés.

a) Mozgási energiájának hányad részét veszíti el a neutron az első ütközésben? Megoldás: az egyenes, rugalmas ütközésnél az ütközés utáni és az ütközés előtti sebességek aránya: v / u = (M-m)/(M+ m), azaz behelyettesítve a szén és a neutron tömegét: v / u = 0,8453 A mozgási energiák aránya a sebességek négyzetének aránya, tehát 0,8453^2. = 0,7145, azaz az energiaveszteség 28,54%.

b) Legalább hányszor kell ütköznie, hogy mozgási energiája 0,025 eV ("szobahőmérséklet" alá csökkenjen? Megoldás: Az ütközések során a maradék energia a feladat által megadott ideális esetben egy mértani sorozat elemeiként számítható, amelynek hányadosa 0,7145. Ebből a szükséges ütközések számára 53 adódik.

4. Egy Geiger-Müller-számláló holtideje az az idő, amely eltelik egy részecske érzékelése után addig, amíg a cső újra képes lesz a detektálásra. Egy adott csőnél ez a holtidő . Egy mérés során ez a cső átlagosan beütést számolt percenként. Becsüljük meg, hogy mekkora a tényleges beütésszám? Megoldás: az összes holtidő egy perc alatt , az "élőidő" tehát 60-6 = 54 s. A teljes beütésszám egyszerű arányossággal adódik: .

5. A CANDU reaktorokban a moderáló közeg nagy tisztaságú (pl. 99,9%) nehézvíz. Ilyen nagy dúsítást csak több lépésben lehet előállítani. A Turnu Severinben (Románia) működő nehézvízüzemben a dúsítás első lépése azon a tapasztalati tényen alapul, hogy a kénhidrogén (H₂S) gáz és a folyékony halmazállapotú H₂O közötti folyadék-gáz határfelületen izotópcsere játszódik le. Az izotópcsere iránya függ a hőmérséklettől: 30 °C körüli hőmérsékleten a könnyű hidrogén megy a gázba a nehézhidrogén helyére, 130 °C körüli hőmérsékleten pedig a csere fordított irányú.

a) Tervezzünk ezek alapján olyan körfolyamatot, amelynek segítségével a nehézhidrogén aránya feldúsítható! Megoldás: a kénhidrogént mint "hordozót" kell használni, körfolyamatban. A dúsítatlan vizet két részre bontjuk: az egyik részből 130 °C-on a gáz "kivonja" a deutériumot (a távozó víz "szegényített" lesz). Ezt a "dúsított" gázt a víz másik, 30 °C-on lévő részén átbuborékoltatva a gázban lévő deutérium a víznek átadódik: dúsított víz és dúsítatlan kénhidrogén távozik. Végeredményben azt értük el, hogy a víz egyik része szegényített, a másik pedig deutériumban dúsított lesz, miközben a H₂S körfolyamat záródott. Sok ilyen fokozatot egymás után kapcsolva megfelelő dúsítás érhető el.

b) Milyen egyéb módszereket ismer a nehézhidrogén dúsítására? Megoldás: Elektrolízis, víz vákuumban történő desztillációja, folyékony hidrogén desztillációja, ammónia és hidrogén közötti katalizált izotópcsere.

6. A légkör felső rétegében a kozmikus neutronok nitrogén atommagokkal történő ütközésekor keletkeznek a radioaktív ¹⁴C (radiokarbon) atommagok az alábbi magreakcióval Tekintsünk egy 1 cm² alapterületű hasábot, amely felnyúlik a Föld felszínétől egészen a légkör felső határáig. Ebben a hasábban átlagosan 2 új radiokarbon atommag keletkezik másodpercenként a fenti reakció eredményeképpen. A keletkezett radioaktív szénizotóp szén-dioxiddá oxidálódik, és részt vesz a légkör és a földi élővilág közötti körforgásban. Hosszú idő alatt egyensúly áll be a légkörben lévő radiokarbon atommagok bomlása és a fenti reakcióval történő keletkezése között. Ennek eredményeképpen a radiokarbon atommagok aránya a stabil szén atommagokhoz időben állandónak tekinthető. Ennek értéke .

a) Becsüljük meg, hogy mekkora tömegű radioaktív ¹⁴C izotóp van a hidro-, bio- és atmoszférában együttesen?

Megoldás: Mivel egyensúly van, másodpercenként ugyanannyi radiokarbon atommagnak kell keletkeznie, mint amennyi elbomlik. A másodpercenként keletkezett atommagok száma a Föld felszínéből és a feladat által megadott 2/cm²-ből meghatározható. Az egyensúly miatt a teljes radiokarbon mennyiség aktivitása is ekkora. Ebből a ¹⁴C atommagok száma és így a teljes tömeg is kiszámítható: 60,3 tonna. Ez azért adja meg a hidro-, bio- és atmoszférában együttesen lévő radiokarbon atommagok tömegét, mert a radiokarbon körforgása a természetben - és így eloszlása a hidro-, bio- és atmoszférában is - sokkal gyorsabb, mint a radiokarbon 5730 éves felezési ideje.

b) Az emberi tevékenység (pl. ipari, közlekedési széndioxid-kibocsátás) hogyan változtatja meg az előbb említett arányt? Megoldás: A fosszilis üzemanyagok elégetése során olyan szén szabadul fel, amelyikben a radiokarbon már elbomlott, koncentrációja csökkent. Így ezzel felborul a természetes arány, kisebb lesz a ¹⁴C aránya.

c) A b) pontban említett változás okozhat-e hibát a ¹⁴C-en alapuló régészeti kormeghatározásokban? Indokoljuk meg a választ. Igen válasz esetén azt is mondjuk meg, hogy fiatalabbnak vagy idősebbnek látszanak-e a régészeti leletek a valódi koruknál? Megoldás: Mivel így a mai levegőben a radiokarbon koncentrációja kisebb, mint régen volt, a leletekben lévő arány magasabbnak tűnik, emiatt fiatalabbnak látszanak. Az északi sarki ismert életkorú - jégből mélyfúrással mintát vesznek, és a benne lévő légbuborékok összetétele alapján korrigálni lehet a méréseket.

7. Milyen lenne a világ, ha a magerő éppúgy hosszú hatótávolságú lenne, mint a Coulomb-erő és a gravitáció? (kitűzte: Marx György †) Megoldás: A magerők töltésfüggetlenek (egyformán hatnak protonok és neutronok között) és mindig vonzók (ilyen szempontból hasonlóak a gravitációhoz). Ha tehát ugyanolyan lenne az erőtörvényük, mint a gravitációnak és a Coulomb-erőnek, akkor a "nukleáris erővonalak" leárnyékolhatatlanok lennének. Mivel a kölcsönhatás erőssége még az elektromosnál is erősebb, ezért semmi sem tudná megakadályozni, hogy ez az erős kölcsönhatás a nukleonokat egymáshoz rántsa. Következésképpen a világon található összes nukleon (protonok, neutronok) egyetlen hatalmas "atommaggá" egyesülnének, amely valószínűleg egy óriási fekete lyukat alkotna.

8. A ²³⁵U hasadásából származó neutronok átlagos élettartama egy reaktorban nagyon rövid, mindössze néhányszor tíz mikroszekundum . Tehát a neutrongenerációk nagyon gyorsan követik egymást, a láncreakció nagyon gyors lefolyású. Az atomreaktorokban a szabályozó rudak elektromechanikus eszközök, amelyek mozgatása másodperces időskálán mérhető. Hogyan lehetséges mégis, hogy ilyen lassú eszközökkel biztonságosan szabályozni lehet a láncreakciót? Megoldás: a késő neutronok teszik lehetővé.

9. Elektronok igen nagy energiára történő felgyorsításához lineáris gyorsítóban kevesebb energia szükséges, mint ciklikus berendezésekkel. Vajon miért? Hasonlítsuk össze ilyen szempontból az ugyanolyan energiára felgyorsított protonokat és elektronokat! Megoldás: A ciklikus berendezésekben a felgyorsított részecskék körpályán mozognak, s így centripetális gyorsulásuk van. A gyorsuló töltések sugárzást bocsátanak ki, s ez energiaveszteséget okoz. Az egy keringésre jutó energiaveszteség a tömeg negyedik hatványával fordítottan arányos, így az elektron gyorsítása ilyen szempontból veszteségesebb folyamat, mint a protoné, mégpedig körülbelül 10¹³ arányban.

10. Képzeljünk el egy kétdimenziós világot! Melyek lennének ebben a világban a mágikus atommagok? Megoldás: Kétdimenziós világban az atommagok állapotait körlapon kialakuló állóhullámokkal lehet modellezni. Minden lényegesen különböző állapotba - a Pauli-elvnek megfelelően - két részecske férne be. Az állapotok energiáját a mozgási energia tag határozza meg, ezért az állapotok sorrendje az energia szempontjából: 1s, 2p, 2s, 3d 3p, 3s, .... Ezekbe az állapotokba rendre a következő számú részecske "fér be": 2, 4, 2, 4, 4, 2, ... . Ha ezek az állapotok mind jól elkülönülnek egymástól energiában, akkor a mágikus számok: 2, 6, 8, 12, 16, 18, ... . Ha például a 2s és a 3d állapotok energiája közel esne egymáshoz ("sd-héj" alakulna ki), akkor a 8-as "kimaradna" a fenti számsorból. A magasabb kvantumszámú állapotoknál az állapotok energia szerinti "sorrendjét" nehéz megjósolni, ezért a további mágikus számok sem adhatók meg biztosan.

A feladat egy atomerőmű-szimulátor működtetése volt. A működés során a megadott határértékek túllépése hibapontokat eredményezett, durva túllépés a reaktor vészleállásához vezetett. A versenyzőknek azzal is számolniuk kellett, hogy egyes szerkezeti elemek (pl. generátorok) túlterhelése növelte azok meghibásodási valószínűségét. A cél az volt, hogy egy körülbelül 300 napos "kampány" során minél több energiát termeljenek, miközben minél kevesebb hibapontot szerezzenek. A szimulált kampány körülbelül 40 perc alatt teljesíthető volt. A számítógépes feladatra rendelkezésre álló 90 perc első részében a versenyzők a program működésével és kezelésével ismerkedhettek meg.

A versenyzők rendelkezésére állt egy felületi szennyezettséget mérő készülék. Ennek a segítségével kellett öt porkeveréket tartalmazó csomagot azonosítaniuk. További információként tudták, hogy négy csomag tömege egyenként 100 g, egy csomagé pedig 200 g volt. A négy 100 g-os csomag közül háromban KCl volt a következő koncentrációkban: 100%, 50%, 25%. A negyedik csomag koncentrációja ismeretlen. A 200 g-os csomagban ugyancsak az ismeretlen koncentrációjú anyag volt. A feladat nemcsak a csomagok azonosítása volt, hanem az ismeretlen koncentráció minél pontosabb meghatározása is.

<>

A verseny döntőjének délelőttjén a tíz elméleti feladat megoldására 3 óra, délután a számítógépes feladatra másfél óra, a kísérleti feladatra szintén másfél óra állt a versenyzők rendelkezésére. Egy-egy feladat teljes megoldása 5 pontot, a számítógépes feladat teljes megoldása 30 pontot, a kísérleti feladat teljes megoldása 20 pontot hozhatott, ez összesen 100 pont lehetett. A versenyzők felkészültségét jellemzi, hogy a legjobb 10 szenior versenyző 69 pont felett teljesített, a legkiválóbb 85 pontot ért el. A legjobb 5 junior versenyző 63 pont felett teljesített, legjobbjuk 71 pontot ért el. Ez a példakitűzőket megnyugtatta: a nem könnyű feladatok megfeleltek a döntőben résztvevők magas fokú felkészültségének. A döntőbeli példák nehézségének összehasonlítására közöljük, hogy szinte minden feladatra érkezett jó megoldás. A legjobb helyezetteket egyetemi felvételi vizsga nélkül felveszik a Budapesti Műszaki és Gazdaságtudományi Egyetem, valamint a tudományegyetemek.

I. díj: KOVÁCS ISTVÁN (85 pont), Berze Nagy János Gimnázium, Gyöngyös, tanára: Kissné Császár Erzsébet

II. díj: RUPPERT LÁSZLÓ (84), Janus Pannonius Gimnázium, Pécs, Keresztesné B. S.

III. díj: BALOGH LÁSZLÓ (81), Fazekas Mihály Fővárosi Gyakorló Gimnázium, Budapest, Horváth Gábor

A legjobb 10 versenyző közt volt egy leány is: Komjáthy Júlia (76 pont) Szekszárdról.

I. helyezett: HEISENBERGER VIKTOR (71), Leöwey Klára Gimnázium, Pécs, Simon Péter

II. helyezett: HANDBAUER PÉTER (69), Leöwey Klára Gimnázium, Pécs, Simon Péter

III. helyezett: DOMJÁN DÁNIEL (66), Zrínyi Miklós Gimnázium, Zalaegerszeg, Pálovics Róbert

A verseny után a példák megoldását Sükösd Csaba (BME) ismertette. Egyúttal tájékoztatást adott a megjelenteknek a paksi 2. sz. reaktorblokknál áprilisban történt üzemzavar lefolyásáról is.

A záróülésen Sükösd Csaba megemlékezett a közelmúltban elhunyt Marx György professzorról, a verseny megalapítójáról és korábbi vezetőjéről. A résztvevők néma felállással tisztelegtek Marx György emlékének. A tanulói díjak átadása után került sor az idei Delfin-díj átadására, amelyet minden évben a tanárok pontversenyében a legjobb eredményt elért tanárnak ítél oda a versenybizottság. Ebben az évben a Delfin-díjat KOVÁCS LÁSZLÓ, a Ságvári Endre Gyakorló Gimnázium (Szeged) tanára kapta.

Az Országos Szilárd Leó Verseny Versenybizottsága egy új díjat is alapított - a Marx György Vándordíjat -, amelyet minden évben a pontversenyben legkiválóbb eredményt elért iskolának ítél oda a Versenybizottság. 2003-ban a Marx György Vándordíjat a ZRÍNYI MIKLÓS GIMNÁZIUM (Zalaegerszeg) nyerte el.

Az ünnepi beszédek után Sükösd Csaba köszönetét fejezte ki a versenyt támogató Paksi Atomerőműnek és a paksi Energetikai Szakközépiskolának, különösképpen Csajági Sándor tanárnak, aki önzetlenül vállalta a szervezés terheinek legnagyobb részét. A versenyt 2004-ben is megrendezzük. A Versenybizottság döntése alapján azonban a verseny tematikáját a nukleáris ismereteken túl kibővítjük a modern fizika egyéb területeivel is.