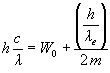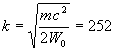Fizikai Szemle 2004/9. 311.o.
VII. SZILÁRD LEÓ NUKLEÁRIS TANULMÁNYI VERSENY
2004 tavaszán rendezte meg a Szilárd Leó Tehetséggondozó Alapítvány és az Eötvös Loránd Fizikai Társulat hetedik alkalommal a Szilárd Leó Nukleáris Tanulmányi Versenyt. A Versenybizottság a 2004-es verseny meghirdetésekor kibővítette a hagyományos tematikát: a nukleáris témák mellé egyéb "modern fizikai" területeket is bevontak a verseny tematikájába.
Ebben az évben 345 középiskolás indult csaknem félszáz iskolából, az eredmények tanúsága szerint jó felkészültséggel. Néhány esetben érzékelhető volt, hogy a tematika kibővítése "meglepte" mind a felkészítő tanárokat, mind pedig a versenyzőket. Az új területekről kitűzött feladatokra kevesebb jó megoldás érkezett, mint a "hagyományos" nukleáris feladatokra. Ez jól mutatja, hogy a versenyeknek milyen fontos szerepük van az oktatott tananyagterületek formálásában. Erős biztatás ez a jövő számára, mert remélhető, hogy a tematika kibővítésével a nukleáris alapismeretek mellé egyéb modern fizikai területek oktatása is felzárkóztatható.
Az első forduló (válogató verseny) 10 példáját az iskolákban lehetett megoldani 3 óra alatt. Kijavítás után a tanárok azokat a megoldásokat küldték be az Eötvös Társulatba, ahol a 9-10. osztályos (junior) versenyzők legalább 40%-os, a 11-12. osztályos (szenior) versenyzők legalább 60%-os eredményt értek el. Ezeket ellenőrizve a bírálóbizottság a legjobb 8 junior versenyzőt és a legjobb 20 szenior versenyzőt hívta be a paksi Energetikai Szakközépiskolában 2004. április 17-én megrendezett döntőre. A behívott szenior versenyzők közül ketten nem tudtak megjelenni, így 18 szenior és 8 junior versenyző vett részt a döntőn. A versenyeken bármilyen segédeszköz használható volt (mobiltelefon és az Internet kivételével). Az alábbiakban ismertetjük a válogató verseny, valamint a döntő feladatait, és a megoldások lényeges gondolatait.
A válogató verseny feladatai
1. feladat. Atomos hidrogéngázt elektronokkal gerjesztünk egy kisülési csőben úgy, hogy a gáz világít. Elegendő-e a gerjesztéshez olyan sebességű elektronokat a gyorsítótérben előállítani, amelyeknek energiája megegyezik a látható fény fotonjainak energiájával? (Válaszát indokolja!)
Megoldás: Nem elegendő a látható fotonokkal megegyező elektronenergia, mivel a többségében alapállapotú atomokat legalább a 3. energiaszintre kell gerjeszteni, hogy a 3 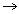 2 atomi elektronátmenet a Balmer-sorozat első látható vonalát létrehozza. Ehhez viszont E3-E1 energiára van szükség, amely 6,4 szerese az E3-E2 kibocsátott foton energiájának.
2 atomi elektronátmenet a Balmer-sorozat első látható vonalát létrehozza. Ehhez viszont E3-E1 energiára van szükség, amely 6,4 szerese az E3-E2 kibocsátott foton energiájának.
2. feladat. Magyarázzuk meg, miért nincs 158-as rendszámú atommag!
Megoldás: A magerők rövid hatótávolságúak, a protonok Coulomb-taszítása viszont hosszú hatótávolságú. Ezért a nagy rendszámú atommagoknál az egyre erősebbé váló Coulomb-taszítás instabillá teszi a magot, és az alfa-bomlással, vagy spontán maghasadással kisebb rendszámú maggá (magokká) bomlik. A megoldásban a 158-as számnak nincs szerepe, csak az a lényeg, hogy "nagy" legyen.
3. feladat. Egy fotocella áramkörébe kondenzátort helyezünk. A bárium-katódot 540 nm hullámhosszúságú fénnyel világítjuk meg.
- Mekkora feszültségre töltődik fel a kondenzátor?
- Hány elektron tölti fel az 5 nF-os kondenzátort?
Adat: a bárium-katód kilépési munkája: 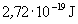
Megoldás: a kondenzátor addig töltődik, amíg a létrehozott elektromos mező meg nem akadályozza, hogy a fotokatódból kilépő elektronok elérjék az anódot. Ekkor eU = Ee, ahol U a kondenzátor feszültsége, Ee pedig az elektronok mozgási energiája a katódból való kilépéskor. Ez utóbbit a fény hullámhosszának és a bárium kilépési munkájának ismeretében az Einstein-egyenletből meghatározhatjuk: 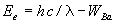 . Az U feszültség ismeretében már a kondenzátor feltöltéséhez szükséges elektronok száma is könnyen kiszámítható.
. Az U feszültség ismeretében már a kondenzátor feltöltéséhez szükséges elektronok száma is könnyen kiszámítható.
4. feladat. A 35000 km/s sebességű elektron olyan homogén mágneses mezőbe jut, amelynek mágneses indukciója merőleges a sebességre és nagysága 17,5 mT.
- Milyen sugarú körpályára kerül az elektron?
- Mekkora frekvenciájú szinkrotronsugárzást bocsát ki a körpályán mozgó részecske?
Megoldás: az elektron körpályán tartásához szükséges centripetális erőt a Lorentz-erő adja:
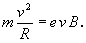
Ebből a körpálya sugara:
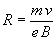 .
.
Körpályán történő mozgás két, egymásra merőleges rezgésből tehető össze: mindkét rezgés frekvenciája = 1/T, ahol T a körülfordulási idő
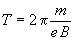 .
.
Az elektron ilyen frekvenciájú sugárzást bocsát ki, hiszen úgy viselkedik, mint egy antenna, amelyben töltések periodikus mozgást végeznek ezen a frekvencián. Bár az elektron sugároz és ezáltal veszít az energiájából, a körülfordulási idő nem változik (hiszen nem függ sem a sebességtől, sem pedig a pálya sugarától). Ezért az elektron ilyen frekvencián mindaddig sugároz, amíg csak bele nem zuhan a középpontba. (A Versenybizottság helyesnek fogadta el azokat a megoldásokat is, amelyek elhanyagolták az elektron folyamatos energiavesztését.)
5. feladat. A neutron bomlásának mérése céljából atomreaktorból származó neutronokat először egy "monokromátorra" ejtünk, amely - hasonlóan a fény- és a röntgensugarak diffrakciójához - csak jól meghatározott 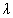 de Broglie-hullámhosszúságú neutronokat enged tovább. Ezt a neutronnyalábot ezután egy hosszú "repülési csövön" vezetjük végig, és a cső 1 méteres szakaszán mérjük a neutronok bomlástermékeit (ld. ábra).
de Broglie-hullámhosszúságú neutronokat enged tovább. Ezt a neutronnyalábot ezután egy hosszú "repülési csövön" vezetjük végig, és a cső 1 méteres szakaszán mérjük a neutronok bomlástermékeit (ld. ábra).
Legalább hány neutronnak kell végigfutni másodpercenként a repülési csövön, ha azt akarjuk, hogy a detektorunk óránként legalább 36 eseményt számláljon?
Adatok: a szabad neutron felezési ideje: T1/2 = 12,8 perc, tömege: 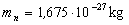 , a monokromátorból kijövő neutronnyaláb hullámhossza:
, a monokromátorból kijövő neutronnyaláb hullámhossza: 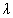 = 0,396 nm, a bomlás detektálásának teljes hatásfoka 1%.
= 0,396 nm, a bomlás detektálásának teljes hatásfoka 1%.
Megoldás: Mivel a detektálás hatásfoka 1%, ezért a csőben óránként 3600 bomlásnak - azaz másodpercenként egy bomlásnak - kell történnie. A csőben lévő neutronok "aktivitása" tehát éppen 1 Bq. Ebből a csőben állandóan lévő neutronok száma meghatározható az
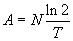
összefüggés segítségével: N = 1108. A neutronok sebessé- ge a de Broglie-összefüggés segítségével meghatározható, és v ~ 1000 m/s adódik. Ez azt jelenti, hogy egy neutron körülbelül 0,001 s-ig tartózkodik a csőben. Azaz 0,001 s alatt kell 1108 neutront "pótolni", vagyis másodpercenként körülbelül 1,1 millió neutronnak kell végigfutnia a csövön.
6. feladat. A Szaturnusz felé utazó Cassini űrhajón a 238Pu-izotóp 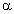 -bomlásakor keletkező hőt használják fel elektromos energia előállítására. Az űrhajó berendezéseinek működéséhez 630 W elektromos teljesítmény szükséges a Szaturnusz körüli pályán.
-bomlásakor keletkező hőt használják fel elektromos energia előállítására. Az űrhajó berendezéseinek működéséhez 630 W elektromos teljesítmény szükséges a Szaturnusz körüli pályán.
- Legalább mekkora tömegű 238Pu-ot használtak fel az áramforrás építéséhez?
- A 238Pu-ot mely tulajdonságai alapján választhatták ki?
Adatok: A 238Pu felezési ideje 88 év. A 238Pu tisztán 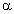 -bomló. Bomlásakor
-bomló. Bomlásakor 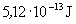 energia szabadul fel, amelynek 90%-a alakul hővé. A hőt pedig 7% hatásfokkal lehet elektromos energiává alakítani.
energia szabadul fel, amelynek 90%-a alakul hővé. A hőt pedig 7% hatásfokkal lehet elektromos energiává alakítani.
Megoldás: a) A hatásfokok figyelembevételével a másodpercenként felszabaduló energia, majd ebből a forrás aktivitása könnyen meghatározható. Az aktivitás ismeretében az
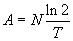
összefüggés segítségével a preparátumban lévő atomok száma, s ebből a preparátum tömege kiszámítható. Eredmény: 30,9 kg.
- A 238Pu tisztán
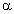
-bomló, ezért a felszabaduló energia könnyen "összegyűjthető", és a sugárzás sem hagyja el a forrást. A felezési idő is fontos: túl hosszú felezési idejű izotópból túl nagy tömeget kellene vinni, túl rövid felezési idejű pedig túl hamar lebomlana.
7. feladat. Mekkora frekvenciájú a hidrogén vonalas színképe Balmer-sorozatának az a spektrumvonala, amelynek hullámhossza 1,19-szorosa a sorozathoz tartozó legkisebb hullámhossznak? Hányadik vonala ez a spektrumnak?
Megoldás: A Balmer-sorozat vonalainak száma végtelen, s a tagok hullámhossza egyre kisebb:
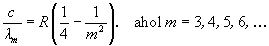
"Legkisebb hullámhossznak" a végtelen, csökkenő sorozat határértékét kell tekintenünk, amikor 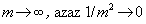 . Tehát
. Tehát
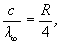
ahol 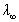 "legkisebb hullámhossz". A feladat szerint
"legkisebb hullámhossz". A feladat szerint 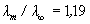 . Ebből m = 5 adódik. Ez azonban csak harmadik vonala a sorozatnak, mivel az első vonalra m = 3.
. Ebből m = 5 adódik. Ez azonban csak harmadik vonala a sorozatnak, mivel az első vonalra m = 3.
8. feladat. A természetben található uránban csupán minden 140-ik atom magja a könnyen hasadó 235U-izotóp (a többi a nehezen hasadó 238U-magot tartalmazza). Ezért az atomreaktorok urán üzemanyagában többszörösére (5-6-szorosára) növelik a 235U-izotópok arányát, azaz dúsítják az uránt.
- Hányszorosára nő meg a dúsított urán aktivitáskoncentrációja (tömegegységenkénti aktivitása) a természetes uránhoz képest, ha a dúsítás mértéke 6-szoros (vagyis az 235U-magok aránya az eredetinek hatszorosára nő)?
- Hány százalékkal csökken a dúsító üzemekben visszamaradó "szegényített urán" aktivitáskoncentrációja, ha a benne visszamaradó 235U-izotópok százalékos aránya 0,7%-ról 0,1%-ra, (azaz az eredeti arány 1/7-re) csökken?
Adatok: Az 238U felezési ideje 4,5 milliárd év, az 235U-é pedig 710 millió év.
Megoldás: a) A teljes aktivitás növekedési aránya csupán 18%-os (ha az aktivitás csak a 235U-tól származna, akkor 600%-os növekedést várnánk).
- Az 1/7 részben szegényített urán aktivitása csupán 97%-ra csökken le. (Ha az aktivitás csak az 235U-tól származna, akkor 1/7
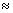
14 %-ra való lecsökkenést várnánk.)
9. feladat. Egy kőzet vizsgálata során az 238U bomlási sorából az alábbi izotópok aktivitását sikerült meghatározni. Értelmezze az eredményt!
Tábl.
Megoldás: Radioaktív bomlási sorban hosszú idő alatt egyensúly áll be, az egymást követő tagok aktivitása megegyezik. Ez a 226Ra-ig teljesülni látszik a fenti táblázatban (az "ingadozások" mérési bizonytalanságokból erednek). Itt van egy "ugrás", az aktivitás hirtelen lecsökken, és a további tagoknál már kisebb értékeket mértek. Az is feltűnik, hogy a táblázatból hiányzik a 226Ra-ot követő 222Rn. Ennek az aktivitását (valószínűleg az alkalmazott mérési módszerek miatt) nem határozták meg. Az "ugrás" magyarázata az, hogy a kőzetből a keletkezett radon egy része - nemesgáz lévén - megszökött, és ezért csak a maradék radon bomlástermékeit találhatjuk meg.
10. feladat. George Gamow: Tompkins úr kalandjai a fizikával című könyvében olyan biliárdgolyókkal játsszák a kvantumbiliárd nevű játékot, amelyek a kvantumőserdőből származó elefántok agyarából készülnek. Így látszik a golyók elmosódottsága, mozgás közben szétterjednek a golyók, valamint a biliárdnál használt fa háromszögbe helyezett, magára hagyott golyó kitölti a háromszöget. Becsüld meg, legalább mekkora ebben a világban a Planck-állandó!
Adatok: A golyó körülbelül 5 cm átmérőjű gömb, tömege 0,15 kg. Ha v = 10 m/s (±10%) sebességgel halad, akkor 2 mm-es elmosódottságot láthatunk a golyó határain.
Megoldás: A Heisenberg-féle határozatlansági összefüggés segítségével h 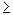 0,015 Js adódik, ami 32 nagyságrenddel nagyobb a Planck-állandó valódi értékénél.
0,015 Js adódik, ami 32 nagyságrenddel nagyobb a Planck-állandó valódi értékénél.
A döntő versenyfeladatai
A Versenybizottság a döntővel kapcsolatban két új elemet vezetett be. Már az első Szilárd Leó-versenyen, 1998-ban a junior kategória versenyfeladatai részben eltértek a "nagyok" feladataitól. Ezt a gyakorlatot a Versenybizottság visszaállította. A másik új elem formai: a feladatok mellé megjelöltük azt is, hogy a feladat kinek az ötlete alapján készült.
1.feladat (mindkét kategória számára, kitűzte: Sükösd Csaba): Egy neutrongenerátor a következő fúziós reakció alapján állítja elő a nagyenergiájú neutronokat: 2H+3H 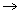 4He + n. Ebben a fúziós reakcióban 2,82 pJ energia szabadul fel. A 200 kV feszültséggel felgyorsított deutérium ionnyaláb áramerőssége 1 mA. Ez a nyaláb olyan céltárgyra esik, amelyben fémben (cirkóniumban) elnyeletett tríciumatomok vannak.
4He + n. Ebben a fúziós reakcióban 2,82 pJ energia szabadul fel. A 200 kV feszültséggel felgyorsított deutérium ionnyaláb áramerőssége 1 mA. Ez a nyaláb olyan céltárgyra esik, amelyben fémben (cirkóniumban) elnyeletett tríciumatomok vannak.
- A nyaláb részecskéinek hányad része okoz fúziót, ha a neutrongenerátor másodpercenként 1010 neutront kelt?
- Másodpercenként mennyi fúziós energia szabadul fel?
- Hogyan aránylik ez az energia ahhoz, amekkora energiával a nyaláb melegíti a céltárgyat?
Megoldás:
- minden fúziós eseményben egyetlen neutron keletkezik, ezért a másodpercenkénti fúziók száma is 1010. Mivel minden fúzióhoz egyetlen deuteron kell, ezért másodpercenként 1010 deuteron okoz fúziót. A nyaláb áramerősségéből a másodpercenként beérkező deuteronok száma kiszámítható:
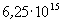 , és így a keresett arány:
, és így a keresett arány: 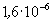 .
.
- A fúziós teljesítmény: 0,0282 J/s.
- A nyaláb teljesítménye
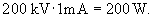 Ezért a keresett arány:
Ezért a keresett arány: 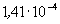
.
2. feladat (mindkét kategória számára, kitűzte: Ujvári Sándor ): A CERN új gyorsítójában (LHC = Large Hadron Collider, Nagy Hadronütköztető) két, egymással szemben futó nyalábban protonokat és antiprotonokat ütköztetnek egymással. Mindkét nyalábban a részecskék lendülete: 7 TeV/c 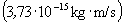 .
.
- Ha egyetlen részecske keletkezne, mekkora lenne ennek tömege?
- Milyen egyéb tulajdonságai lennének ennek a részecskének?
Megoldás:
- Mivel egymással szemben azonos lendülettel futó nyalábok ütközéséről van szó, a keletkezett egyetlen részecske a laboratóriumi rendszerben állna, azaz a teljes rendelkezésre álló (relativisztikus) energia ennek a részecskének a tömegére fordítódna, azaz a részecske tömegére Mc2 = 14 TeV (itt elhanyagoltuk a proton és az antiproton nyugalmi tömegét, amelyek figyelembe vétele tízezreléknyi kis korrekciót jelentene).
- Ha egyetlen részecske keletkezne, a megmaradási tételek miatt a következő tulajdonságokkal kellene rendelkeznie:
- töltése: 0 (elektromosan semleges)
- bariontöltése: 0 (azaz nem lehetne barion)
- leptontöltése: 0 (azaz nem lehetne lepton sem).
Ilyen részecskéket ismerünk. Az egyik ilyen a foton, de annak 0 a nyugalmi tömege, ezért ezt kizárhatjuk. A másik ilyen részecskecsalád a mezonok családja. Ismerünk nehéz mezonokat is, bár ilyen nehezeket még nem. Ha tehát egyáltalán ilyen "egyetlen" részecskére vezető reakció létrejönne, annak igen nehéz, elektromosan semleges mezont kellene létrehoznia.
3. feladat (mindkét kategória számára, kitűzte: Vastagh György): A maghasadás során keletkező 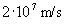 sebességű neutronokat nehézvízzel 1 km/s sebességűre akarjuk lefékezni. Legalább hány ütközés szükséges ehhez?
sebességű neutronokat nehézvízzel 1 km/s sebességűre akarjuk lefékezni. Legalább hány ütközés szükséges ehhez?
Megoldás: Egyetlen egyenes ütközésben a neutron a sebességének legfeljebb 2/3-ad részét veszíti el (marad az eredeti sebességének 1/3-ad része). Ezt a rugalmas ütközések elemi mechanikájával láthatjuk be. Feltételezve, hogy minden ütközés egyenes ütközés, a neutron sebessége mértani sort alkot, ahol az egymást követő tagok hányadosa 1/3. N db ütközés után tehát a neutron sebessége:
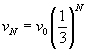 .
.
Ismerve a "végsebességet", ebből logaritmálással N > 9 adódik. A neutronnak tehát legalább 10-szer kell ütköznie. (A valóságban az ütközések nagyobb része nem egyenes ütközés, ezért azokban a neutron energiavesztesége kisebb. Tehát 10-nél biztosan több ütközésre van szükség.)
4. feladat (mindkét kategória számára, kitűzte: Sükösd Csaba): Rutherford abból következtetett az atommagok kis méretére, hogy az aranyfóliára ejtett alfa-részecskék egy része nagy szögben térült el, szinte visszapattant. Vajon hogyan győződhetett meg Rutherford arról, hogy ez a nagyszögű eltérülés nem abból származott, hogy az alfarészecskék egy része sok atommal ütközött a fóliában, és a sok egymás utáni (kisszögű) eltérülés adódott össze, és hozta létre végeredményben a nagyszögű eltérülést?
Megoldás: Gondolatban szeleteljük fel a fóliát olyan vékony rétegekre (pl. atomi rétegek), amelyeken már biztosan nem szóródhatnak az alfa-részecskék egynél többször (lehet, hogy egyszer sem, de legfeljebb egyszer). Vegyünk most egy N ilyen rétegből álló fóliát, és tekintsük csak azokat a részecskéket, amelyek pontosan egyszer szóródtak. Ezeknek a száma arányos lesz N-nel, hiszen N-féleképpen választhatjuk ki azt az egyetlen réteget, amelyen a szóródás történt.
Tekintsük most azokat a részecskéket, amelyek áthaladásuk során pontosan kétszer szóródtak!
Ezeknek a száma arányos lesz
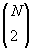
értékével, hiszen ennyiféleképpen választhatunk ki két réteget az N-ből. Ez a szám N másodfokú függvénye, hiszen
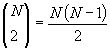
Vegyük észre, hogy a "atomi rétegek száma" (N) tulajdonképpen a fólia vastagságával arányos. Ezért az egyszer szórt részecskék száma a fólia vastagságának lineáris függvénye, a kétszer szórtaké a fólia vastagságának másodfokú függvénye stb. Rutherfordnak tehát meg kellett vizsgálnia az eltérült részecskék számát különböző vastagságú fóliákra. Ha egyenes arányosságot talált, biztos lehetett abban, hogy a nagyszögű eltérülés egyedi eseményektől (egyszeres szórásból) származik, és nem többszörös szórásból. Rutherford ezeket a kísérleteket elvégezte, és a kísérleti eredmények egyértelműen az alfarészecskék egyszeri szóródását bizonyították. (A mai kísérletekben is hasonló módszerrel vizsgálják meg, hogy egy céltárgy "elegendően vékony-e" az adott kísérletben, azaz, hogy ott is csak egyszeri kölcsönhatások játszódnak-e le.)
5. feladat (mindkét kategória számára, kitűzte: Berta Miklós ): Amikor egy töltött részecske átlátszó közegben nagyobb sebességgel mozog, mint a fény közegbeli terjedési sebessége, Cserenkov-sugárzást bocsát ki. Tegyük fel, hogy egy részecskenyaláb, amelyben 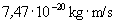 lendületű mü-mezonok és pi-mezonok keveréke halad, átlátszó közegből készült detektorra esik. Mekkorára válasszuk a detektor anyagának törésmutatóját, hogy a detektor csak a mü-mezonokat detektálja a Cserenkovsugárzás segítségével?
lendületű mü-mezonok és pi-mezonok keveréke halad, átlátszó közegből készült detektorra esik. Mekkorára válasszuk a detektor anyagának törésmutatóját, hogy a detektor csak a mü-mezonokat detektálja a Cserenkovsugárzás segítségével?
Adatok: 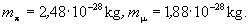
Megoldás: Mivel a detektornak csak a kisebb tömegű, ezért nagyobb sebességű mü-mezonokat kell detektálnia, ezért a közegbeli fénysebességnek a mü-mezonok sebességénél kisebbnek, de a pi-mezonok sebességénél nagyobbnak kell lennie. Tehát:
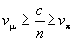 .
.
A részecskék sebességét a relativisztikus képletből lehet meghatározni a lendületük és a nyugalmi tömegük ismeretében:
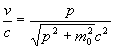 .
.
Behelyettesítés után az eredmény: 1,25 < n < 1,41.
6. feladat (mindkét kategória számára, kitűzte: Szűcs József ): Egy W0 = 0,64 aJ kilépési munkájú fémet monokromatikus fénnyel világítunk meg.
- Milyen hullámhosszúságú (milyen színű) fényt használjunk, hogy a fény hullámhosszának és a fémből kilépő maximális sebességű elektron de Broglie-hullámhosszának aránya a legnagyobb legyen?
- Határozzuk meg az arány maximális értékét!
Megoldás: a) A fotoeffektus
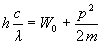
egyenletébe helyettesítsük be az elektron de Broglie-féle hullámhosszát:
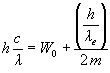
Ebből
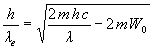 .
.
Szorozzuk be mindkét oldalt 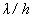 -val, s kapjuk a hullám hosszak arányát:
-val, s kapjuk a hullám hosszak arányát:
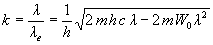 .
.
Kiemelés után kapjuk:
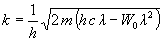 .
.
A gyök alatti, (a fény hullámhosszát tekintve másodfokú) kifejezésnek a zérushelyei 0 és hc/W0 (ez éppen a 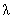 H határhullámhossz). A szélső érték
H határhullámhossz). A szélső érték 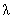 H / 2-nél, azaz
H / 2-nél, azaz 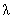 max = hc / 2W0
max = hc / 2W0 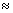 620 nm-nél van. Ez körülbelül piros fény.
620 nm-nél van. Ez körülbelül piros fény.
b) A maximumértékére pedig a
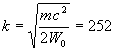
értéket kapjuk.
7. feladat (mindkét kategória számára, kitűzte: Sükösd Csaba): Andris és Brigitta vitatkoznak:
A: Olvastam, hogy újabban egyre jobb eredményeket érnek el a hidrogén üzemanyagként való hasznosításában. Vannak olyan üzemanyagcellák, amelyek a hidrogén segítségével közvetlenül elektromos áramot állítanak elő. Az autóiparban is át lehetne térni a benzinről a hidrogénmeghajtásra. Ha ez megvalósulna, el lehetne felejteni az üvegházhatást okozó széndioxid-problémát, mert sem a hidrogén égésekor, sem pedig az üzemanyagcellákban nem keletkezik szén-dioxid!
B: Szerintem a kérdés nem ilyen egyszerű. A hidrogéntechnológia bevezetése önmagában még nem oldja meg az üvegházhatást, mert …. Ahhoz az kellene, hogy ….
Vajon hogyan érvelt Brigi?
Megoldás: A hidrogén nem energiaforrás, hiszen természetes állapotban nem áll rendelkezésre a Földön, csak energiahordozó. Ez azt jelenti, hogy előbb elő kell valahogyan állítani, és csak ez után lehet használni (mint ahogyan a villamos energia sem energiaforrás, csak energiahordozó). A hidrogén előállításához (pl. víz elektrolízise) energia kell, legalább annyi, mint amennyi energiát a hidrogén elégetésével majd visszanyerünk. A széndioxid- kibocsátás tehát csak akkor lenne mérsékelhető a hidrogéntechnológiával, ha a hidrogén előállításához is szén-dioxidmentes energiaforrást (vízenergia, atomenergia) használnánk.
8. feladat (mindkét kategória számára, kitűzte: Sükösd Csaba): Álmodban különös világban jártál: nem léteztek gömbölyű dolgok. Minden szögletes volt, még az atomok is kocka alakúak voltak. Fizikaórán felszólítottak, és megkérdezték, hogy milyen rendszámú az első két nemesgáz? Már majdnem rávágtad az ébrenlétből ismert választ, amikor hirtelen rájöttél, hogy ez a válasz itt nem lenne jó…
Milyen két számot mondanál az álombeli tanárnak?
Megoldás: Természetesen a kockavilágban is a legalacsonyabb energiájú állapot a csomómentes állapot, s mivel ebből csak egyféle van, ebbe itt is 2 elektron "fér el" a Pauli-elvnek megfelelően. Ezért az első nemesgáz rendszáma itt is 2. A kocka alakú világban, ahol semmi "gömbölyű" nincs, nincsenek csomógömbök sem, csak csomósíkok. Ezért a következő állapot az egy csomósíkos állapot. Ebből azonban 3 db lényegesen különböző lehet (a tér három irányának megfelelően), s a kocka szimmetriája miatt ezek azonos energiájúak. Ezek mindegyikébe a Pauli elvnek megfelelően 2-2 elektron fér. Ez összesen 6 elektront jelent az egy csomósíkos állapotokban. Ezért a következő "nemesgáz" elektronjainak száma: 8.
9. feladat (a junior kategória számára, kitűzte: Kopcsa József ): A 222,02 u magtömegű 222Rn izotóp 5,48 MeV 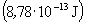 energiájú és 4,0015 u tömegű alfa-részecske kibocsátásával bomlik. Milyen sebességgel lökődik vissza a maradékmag?
energiájú és 4,0015 u tömegű alfa-részecske kibocsátásával bomlik. Milyen sebességgel lökődik vissza a maradékmag?
Adat: az atomi tömegegység u = 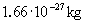
Megoldás: Az atommag-reakció: 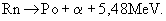 Ebből előbb a Po atommag tömege határozható meg, majd a lendületmegmaradás alapján a visszalökődött mag sebességét kapjuk.
Ebből előbb a Po atommag tömege határozható meg, majd a lendületmegmaradás alapján a visszalökődött mag sebességét kapjuk.
10. feladat (a junior kategória számára, kitűzte Kaszás Dezső): A Duna vizében a trícium aktivitáskoncentrációja átlagosan 6 Bq/liter. Számolja ki, hogy a vízben lévő hidrogénizotópok hányadrésze a trícium! (A trícium felezési ideje 12,3 év.)
Megoldás: 18 g vízben Avogadro-számnyi vízmolekula, és dupla annyi hidrogénatom van. Ugyanennyi víz aktivitásából a tríciummagok száma meghatározható, amiből a keresett arány azonnal adódik. Eredmény: 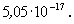
9. feladat (a szenior kategória számára, Károlyházi Frigyes feladata alapján kitűzte: Sükösd Csaba): p = mv lendületű, vízszintesen haladó elektronnyalábot nagy kiterjedésű fémlemezre ejtünk, amelyen kis, d átmérőjű kör alakú nyílás van. A lemez mögött L távolságra lévő fényképezőlemezt a becsapódó elektronok megfeketítik.
- Mekkora legyen a nyílás d átmérője, hogy a folt a lehető legkisebb legyen?
- Mekkora lesz ekkor a folt átmérője?
Segítség: gondoljon az elektronok de Broglie-hullámhosszára, és a Heisenberg-féle határozatlansági összefüggésre.
Megoldás: Ha az elektronsugár a klasszikus fizika szabályai szerint viselkedne, akkor egy párhuzamos nyaláb a d átmérőjű nyíláson áthaladva éppen d átmérőjű foltot hagyna az ernyőn. A foltátmérő csökkentése érdekében tehát csökkenteni kell a d átmérőt nagyon kicsire. Az átmérő csökkentésével azonban egyre inkább számításba kell venni az elektronok hullámtulajdonságát is, hiszen kis résen (lyukon) a részecskehullám elhajlik, és behatol a rés mögé. Nagyon kis rés tehát nagyon nagy elhajlást okoz, és emiatt az ernyőn megjelenő folt is egyre nagyobb lesz.
Az elhajlást a Heisenberg-féle határozatlansági összefüggés segítségével becsülhetjük meg. Tekintsük most csak az egyik dimenziót, az ernyő síkjában. (A másik dimenzióra vonatkozóan hasonló a helyzet.) A lyukon áthaladó részecskéket "beszorítottuk" a lyuk méretére, a helyüket - például x irányban - d pontossággal meg tudjuk mondani, azaz  x = d. Ennek megfelelően a résen áthaladt hullám lendületvektorának is lesz egy
x = d. Ennek megfelelően a résen áthaladt hullám lendületvektorának is lesz egy
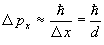
bizonytalansága. A rajz alapján
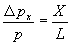
(hasonló háromszögek). A folt átmérője tehát:
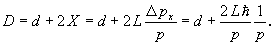
Szorozzunk végig d 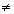 0-val, és rendezzük át az egyenletet:
0-val, és rendezzük át az egyenletet:
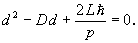
A másodfokú egyenlet diszkriminánsa:
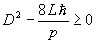
kell ahhoz, hogy az egyenlet megoldható legyen. Ebből kapjuk:
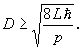
A folt átmérője éppen akkor a legkisebb, amikor
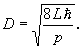
Mivel a diszkrimináns ekkor éppen 0, ezért a lyuk átmérője
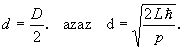
Megjegyzés: A minimum helyét természetesen a
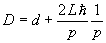
egyenlet első deriváltjának 0 helye alapján egyszerűbben meg lehetne keresni, de a differenciálás - sajnos - nem középiskolai tananyag.
10. feladat (a szenior kategória számára, kitűzte Sükösd Csaba): Vajda János írta Az Üstökös című versében:
Az égen fényes üstökös; uszálya
Az ég felétől, le a földre ér.
Mondják, ez ama "nagy", melynek pályája
Egyenes, vissza hát soha se tér.
Haladhat-e egyenes pályán egy test a Naprendszerben anélkül, hogy a Napba zuhanna? Indokolja meg a választ! (A bolygók hatását hanyagoljuk el!)
Megoldás: A Naptól R távolságra levő, m tömegű objektumra a Nap
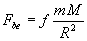
vonzóerőt gyakorol. Ez az erő a Nap középpontja felé - "befelé" - mutat. A Nap azonban - sugárzása révén - kifelé mutató erőt is tud gyakorolni, a fénynyomás segítségével. A fénynyomás abból ered, hogy a Napból származó fotonok ütköznek a testtel. Ha elnyelődnek, p lendületet adnak át a testnek, ha pedig visszaverődnek, akkor 2p lendületet adnak át. Ha a Nap időegységenként N fotont bocsát ki, akkor egy A felületű, a Naptól R távolságra lévő testre időegység alatt
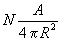
foton esik. Ezzel lesz arányos a fénynyomásból származó, a Naptól kifelé mutató erő:
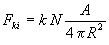
(k egy arányossági tényező). A kiszemelt testre ennek a két erőnek az eredője hat (hiszen a bolygók hatásától eltekintünk a feladat szerint). A két erő eredője:
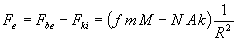 .
.
Innen látható, hogy ha valamilyen pontban e két erő eredője éppen 0, azaz
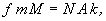
akkor ez a Naptól bármilyen távolságra is 0 lesz. Akárhol halad is tehát ez a test, a rá ható erők eredője mindig 0 lesz, azaz egyenes pályán fog mozogni.
A fénynyomás nagyon kis erőket tud csak létrehozni. Ezért ahhoz, hogy az erők egyensúlya teljesüljön, az objektumnak kis m tömegűnek (kis gravitációs vonzás) és nagy A felületűnek (sok foton csapódjon be időegység alatt) kell lenni. Gömbszimmetrikus testek esetén a test tömege a sugár köbével csökken, a felülete azonban csak a sugár négyzetével. Ezért elegendően kicsiny objektumok esetén a fénynyomásból származó erő akár meg is haladhatja a gravitációs vonzóerőt, és "kifújhatja" a Naprendszerből ezeket a parányi részecskéket. Tehát az "egyenes pályájú" égi objektum nagyon kicsike…
Számítógépes feladat: Mikroszkóp látóterébe porlasztott olajcseppek elektromos töltését kellett megmérni egy Millikan-kísérletet szimuláló program segítségével. A programhoz részletes használati utasítást kaptak a versenyzők. A feladat végrehajtása során a versenyzők nem az elméleti tudásukat mérték össze. Mivel a kísérlet végrehajtásához, a mérési adatok kiértékeléséhez, valamint a jegyzőkönyv megírásához rendelkezésre álló idő mindössze 90 perc volt, a használati utasításban az olajcsepp töltésének meghatározásához szükséges elméleti összefoglalót is megadtuk, a képletekkel együtt. Voltak versenyzők, akik a 90 perc alatt 6-8 olajcsepp töltését is megmérték és az elemi töltést meglepően pontosan meg tudták határozni.
Kísérleti feladat: A feladat béta-sugarak különböző fémlemezekről történő visszaverődésének vizsgálata volt. A versenyzők rendelkezésére állt egy GM-csöves detektor, valamint egy egyik oldalán zárt, vékony alumínium csőbe helyezett, szabad szintnél kisebb aktivitású 90Sr sugárforrás. A versenyzőkkel közöltük, hogy a 90Sr tisztán bétasugárzó. Az asztalon voltak még különböző anyagokból (Al, Fe, Cu, Pb) készült, 2 mm vastag fémlemezek, valamint Bunsen-állványok fogókkal, amelyekkel a forrást, a detektort és a fémlemezeket különböző geometriai elrendezésben rögzíteni lehetett. Két kérdést tettünk fel a versenyzőknek:
- Milyen geometriai elrendezés mellett kapunk optimális jel/háttér arányt? A "jel" itt a visszavert béta-intenzitást jelenti.
- A kiválasztott geometriai elrendezésben milyen intenzitást találnál egy Au-lemezről történő visszaverődésnél?
Értékelés
A verseny döntőjének délelőttjén a tíz elméleti feladat megoldására 3 óra, délután a számítógépes feladatra másfél óra, a kísérleti feladatra szintén másfél óra állt a versenyzők rendelkezésére. Egy-egy feladat teljes megoldása 5 pontot, a számítógépes feladat teljes megoldása 25 pontot, a kísérleti feladat teljes megoldása 25 pontot hozhatott, ez összesen 100 pont lehetett. Úgy tűnt, hogy a versenyzőket a döntőben is meglepte a kibővített tematika, mert az idén valamivel alacsonyabb pontszámok születtek, mint 2003-ban. A legkiválóbb szenior versenyző 78 pontot ért el (tavaly 83 pont volt a legjobb eredmény). A legjobb junior versenyző 83 pontot ért el (tavaly 71 pont volt a legjobb). Legnehezebbnek a szenior versenyzők 9. és 10. feladata bizonyult - ahogyan arra a Versenybizottság számított is. De még a 9. feladatra is érkezett két helyes megoldás. A számítógépes feladat az idén is sikert aratott: a programot sok diák és tanár kérte el Sükösd Csabától. A Versenybizottságnak meglepetést okozott a kísérleti készség vártnál is nagyobb hiánya. Biztosak vagyunk abban, hogy a diákok legnagyobb része a döntőben már olyan elméleti felkészültségű, hogy pontosan tudják, hogy a béta-sugarak nem hatolnak át fémlemezeken (hacsak az a lemez nem nagyon vékony, de ilyenkor fóliának nevezzük). Ugyanakkor a kísérlet során a kísérletet felügyelő tanároknak egy idő után be kellett avatkozni, és megmondani a versenyzőknek, hogy a csőből csak a nyitott végén jön ki a béta-sugárzás, mert sokan más irányokkal próbálkoztak. Hasonlóan, fel kellett arra hívni a figyelmet, hogy a sugárzás, ami kijön a csőből, többé-kevésbé kollimált, irányított. Ez jó példa arra, hogy a diákok gyakran nem tudják a gyakorlatban "aprópénzre" váltani a fejükben lévő elméleti tudást. Ezen valószínűleg lehetne segíteni több (modern fizikai) tanulói kísérlettel az iskolákban.
A legjobb helyezettek - a hagyományoknak megfelelően - felvételi kedvezményeket kapnak a Budapesti Műszaki és Gazdaságtudományi Egyetemen, valamint a tudományegyetemeken mérnök-fizikus, fizikus és fizikatanár szakokon.
2003-ban a Szilárd Leó-verseny első helyezettje (KOVÁCS ISTVÁN, Gyöngyös) meghívást kapott Csermely Péter egyetemi tanártól, a Kutató Diákokért Alapítvány vezetőjétől arra, hogy vegyen részt a Kutató Diákok Országos Konferenciáján, a káptalanfüredi táborban. Hadd idézzem Csermely Péter professzornak a Szilárd Leó-verseny versenybizottságához 2004 tavaszán írt levelének részletét:
"… Nagyon köszönöm, hogy tavaly értesített a Szilárd Leó-verseny győzteséről. Hadd mondjam el, hogy a tavalyi győztes, Kovács István (aki jelenleg évfolyamelső a fizikus szakon) közben a laboratóriumomban vállalt diákkörös munkát, és amerikai professzortársaim szerint is igen közel áll ahhoz, hogy élete első igen komoly tudományos közleményét megírja. A fentieken felbuzdulva hadd kérjem arra, hogy idén is küldje el nekünk a verseny győztesének nevét, e-mail-címét, postacímét és mobiltelefon-számát, hogy a diákot a Kutató Diákok VIII. Országos Konferenciájára (változatlanul ingyenesen) meghívhassuk 2004. július 12 és 17 között…"
Ennek alapján a Szilárd Leó-verseny szenior kategóriájának idei győztese az idén is részt vehet a tábor munkájában.
2004-ben a díjakat a következő diákok kapták:
Szenior kategória:
- VÍGH MÁTÉ (78 pont), PTE Babits M. Gimnázium (Pécs), tanára Koncz Károly,
- PAPP GERGELY (73), Batthyányi K. Gimnázium (Szigetszentmiklós), Bülgözdi László,
- BORSÓS DÁVID (60), Boronkay Gy. Műszaki Középiskola és Gimnázium (Vác), Jendrék Miklós.
A döntő résztvevői közt egy leány volt: Lantos Judit Hódmezővásárhelyről.
Junior kategória:
- SZÉCHENYI GÁBOR (83), Verseghy F. Gimnázium (Szolnok), Pécsi István,
- MOLNÁR KRISTÓF (63), Zrínyi M. Gimnázium (Zalaegerszeg), Pálovics Róbert,
- VINCZE JÁNOS (44) Fazekas M. Gimnázium (Debrecen), Takács Kálmán.
A záróülésen a tanulói díjak és oklevelek átadása után került sor az idei Delfin-díj átadására, amelyet minden évben a tanárok pontversenyében a legjobb eredményt elért tanárnak ítél oda a versenybizottság. Ebben az évben a Delfin-díjat SIMON PÉTER, a Leöwey Klára Gimnázium (Pécs) tanára kapta. A Marx György Vándordíjat - amelyet minden évben a pontversenyben legkiválóbb eredményt elért iskolának ítél oda a Versenybizottság - idén a BORONKAY GY. MŰSZAKI KÖZÉPISKOLA ÉS GIMNÁZIUM (Vác) nyerte el.
Az ünnepi beszédek után Sükösd Csaba köszönetét fejezte ki a versenyt támogató Paksi Atomerőműnek és a paksi Energetikai Szakközépiskolának, különösképpen Csajági Sándor tanárnak, aki 2004-ben is önzetlenül vállalta a szervezés terheinek legnagyobb részét. A versenyt 2005-ben is megrendezzük. A versenyfelhívást és a tematikát alább közöljük.
Bátorítjuk a határon túli magyar tannyelvű iskolák tanulóit is arra, hogy nevezzenek be az Országos Szilárd Leó Fizikaversenyre.
Sükösd Csaba
BME Nukleáris Technika Tanszék
![]() 2 atomi elektronátmenet a Balmer-sorozat első látható vonalát létrehozza. Ehhez viszont E3-E1 energiára van szükség, amely 6,4 szerese az E3-E2 kibocsátott foton energiájának.
2 atomi elektronátmenet a Balmer-sorozat első látható vonalát létrehozza. Ehhez viszont E3-E1 energiára van szükség, amely 6,4 szerese az E3-E2 kibocsátott foton energiájának. 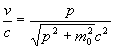 .
.