Fizikai Szemle honlap |
Tartalomjegyzék |
Perjés Zoltán
KFKI, RMKI
Az egyetemes tömegvonzás törvényeit a XX. század első évtizedeiben fogalmazta meg Einstein. A gravitációs törvények keretelmélete az általános relativitáselmélet, amelyben e jelenségkör a tér és az idő geometriai tulajdonságaival válik egyenértékűvé. A relativitáselmélet a kor természettudományos gondolkodóinak heves vitái közepette keletkezett, és az eltelt közel egy évszázad során ezek a viták meg-megújultak a szakértők körében, de laikusok soraiból is gyakran hangzik el kétkedő hang az elmélet érvényességét illetően. Ennek ellenére az elmélet - a kvantumfizikával együtt - a természettudományok alapvető tanításává érett. Miképpen magyarázható, hogy - a kvantumelmélettel ellentétben, melynek fontossága nem csekélyebb - az általános relativitáselmélet újból és újból kivívja a közönség figyelmét? Ebben az egyik kétségtelen tényező az a merészség, amellyel az emélet az olyan alapvető fogalmakhoz nyúl hozzá, mint a tér és az idő. Az ennek befogadásához szükséges szemléletváltás nemcsak a fizika területén kívül tevékenykedők, de még az abban jártas fizikusok számára is komoly kihívást jelent.
Az első szemléleti akadályt a távolságok mérésekor kell leküzdenünk. Derékszögű koordinátákkal az (x, y,z) pont és a szomszédos (x+dx, y+dy, z+dz) pont ds távolságát a Pitagorasz-tétellel kapjuk meg:
![]()
![]()
Itt c a fény sebessége. Ezzel a módosított távolságmérési utasítással olyan természetleírást érünk el, amely - különösen a fény sebességét megközelítő rendszerekre - a korábbi leírásnál sokkal pontosabb lesz. Ez a pontos leírás ma már nemcsak az alapkutatásban, de számos műszaki alkalmazásban is nélkülözhetetlen. Példaként említhetjük a részecskegyorsítók tervezését vagy a globális helymeghatározó rendszer (GPS) működtetését.
Az ekvivalenciaelv
A szemléletváltás másik fordulata a tömegvonzás leírásához szükséges. Ennek alapja az a megfigyelés, hogy mindenfajta test azonos módon mozog a gravitációs térben. Ennek merész magyarázata Einstein nyomán az, hogy a tömegvonzás voltaképpen a tér és az idő geometriájának következménye. A gyenge ekvivalenciaelv azt állapítja meg, hogy a gravitációs gyorsulás független az anyagi minőségtől. Az elvet úgy ellenőrizhetjük, hogy összehasonlítjuk két különböző anyagú test gravitációs gyorsulását. Legyen a két test, A és B, tehetetlen tömege m és súlyos tömege M. Bevezetjük az Eötvös-paramétert a következőképpen:
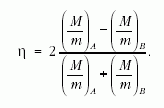
E paraméter segítségével jellemezhetjük az ekvivalenciaelv ellenőrzésére végrehajtott kísérletek pontosságát ( 1. táblázat ).
A PPN keretelmélet
Az általános relativitáselméletben kiteljesedik Bolyai János víziója, aki már a XIX. században kikövetkeztette a görbült terek létezését. Ilyen görbült terekben nem tartható fenn a távolságmérés derékszögű háromszögeken alapuló módszere. Az (1) mérési eljárás helyett az általánosabb
![]()
mérési utasítást kell végrehajtani az ![]() és
és ![]() koordináták segítségével. Einstein nyomán az itt kétszer előforduló indexekre összegeznünk kell. Az (1) és (2) képletek összehasonlításával látjuk, hogy gravitáció távollétében és derékszögű koordinátákban a gik mértéktenzor komponensei: és a többi komponense zérus. Más esetekben (például polárkoordináták választásakor) a komponensek más értéket vesznek fel. Az általános relativitáselméletben a gravitációs egyenletek határozzák meg minden esetben a komponensek alakját.
koordináták segítségével. Einstein nyomán az itt kétszer előforduló indexekre összegeznünk kell. Az (1) és (2) képletek összehasonlításával látjuk, hogy gravitáció távollétében és derékszögű koordinátákban a gik mértéktenzor komponensei: és a többi komponense zérus. Más esetekben (például polárkoordináták választásakor) a komponensek más értéket vesznek fel. Az általános relativitáselméletben a gravitációs egyenletek határozzák meg minden esetben a komponensek alakját.
Az elmúlt évtizedek szellemi áramlataiban sokféle elmélet látott napvilágot a gravitációs jelenségek leírására. Ezek a javaslatok általában megkérdőjelezték a relativitáselmélet valamely posztulátumát, és más számszerű következményeket vezettek le a megfigyelhető gravitációs jelenségekre. Velük egy időben igen sok kísérleti ellenőrzést hajtottak végre a kérdéses jelenségekre. Amint ezek a mérések egyre javuló hibával ellenőrizték az elméletek jóslatait, az alternatív elméletek jóslatai sorra helytelennek mutatkoztak, és az általános relativitáselmélet megerősödve került ki ebből a versenyből.
Ahhoz, hogy egy ilyen alternatív elmélet járható legyen, három kritériumot kell kielégítenie: önkonzisztencia, teljesség és hogy összhangban legyen a korábbi kísérletekkel. A kísérletek újra és újra megerősítenek további két kritériumot a gravitációelméletekkel szemben: 1) A téridőnek van (2) mértéktenzora, és 2) ez a metrika kielégíti
| 1. táblázat Az ekvivalenciaelv ellenőrzése |
||||
| év | kísérlet | módszer | vizsgált anyag | 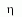 |
| 1686 | Newton | inga | különféle | 10-3 |
| 1832 | Bessel | inga | különféle | 10-5 |
| 1922 | Eötvös, Pekár és Fekete [4] | torziós inga | különféle | 2×10-9 |
| 1935 | Renner | torziós inga | különféle | 2×10-9 |
| 1964 | Roll, Krotkov és Dicke[5] | torziós inga | Au és Al | 10-11 |
| 1972 | Briginszkij és Panov [6] | torziós inga | Pt és Al | 10-12 |
| 1976 | Worden | mágneses lebegtetés | Ni és a Föld | 2×10-5 |
| 1982 | Keiser és Faller | úsztatás | Cu és W | 6×10-12 |
| terv | Worden és Everitt [7] | mesterséges hold | különféle | 10-15-10-9 |
A tíz PPN-paraméter |
||
| paraméter | mit mér a relativitáselmélethez képest | értékeaz ált. rel.elm.-ben |
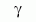 |
Mennyire görbíti a 3-dimenziós teret egységnyi tömeg | 1 |
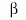 |
g00 szuperpozíciós törvénye mennyire nemlineáris | 1 |
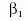 |
Mennyi gravitációt (g00) kelt egységnyi kinetikus energia | 1 |
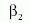 |
Mennyi gravitációt (g00) kelt egységnyi potenciális energia | 1 |
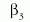 |
Mennyi gravitációt (g00) kelt egységnyi nyugalmi (belső) energia | 1 |
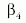 |
Mennyi gravitációt (g00) kelt egységnyi nyomás | 1 |
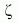 |
Mennyivel több gravitációt (g00) kelt egységnyi radiális kinetikus energia (a megfigyelő irányában), mint a transzverzális kinetikus energia | 0 |
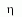 |
Mennyivel több gravitációt (g00) kelt a radiális feszültség, mint a transzverzális | 0 |
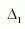 |
Mennyire vonszolja magával a tehetetlenül mozgó koordinátákat (g00) egységnyi impulzusmomentum | 1 |
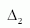 |
Mennyivel erősebben vonszol az impulzus radiális irányban, mint transzverzálisan | 1 |
Áttekintés a vöröseltolódás méréseiről |
|||
| év | kísérlet | módszer | 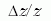 |
| 1960-65 | Pound-Rebka-Snider [8] | Mössbauer-emitterről lehulló fotonok | 10-2 |
| 1962 | Brault | Nap Na D1-vonala | 5×10-2 |
| 1969 | Jenkins | kristály oszcillátoróra a GEOS-1 fedélzetén | 9×10-2 |
| 1972 | Hafele és Keating | céziumórák repülőgépeken | 10-1 |
| 1977 | Allez és társai | rubídiumórák repülőgépeken | 2×10-2 |
| 1976 | Vessot és Levine | hidrogénmézer rakétán | 2×10-4 |
| terv | Nordtvedt | hidrogénmézer vagy SCSO napközeli szondán | 10-6 |
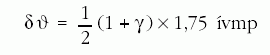
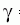 = 1 PPN-paraméter jellemzi. A newtoni gravitációelméletben
= 1 PPN-paraméter jellemzi. A newtoni gravitációelméletben
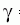 = 0. Az általános relativitáselmélet első kísérleti
igazolását 1919-ben végezték el egy teljes napfogyatkozás
alkalmával. Ezek a mérések meglehetősen pontatlanok
voltak, de mintegy harminc százalékos hibán belül
igazolták a relativitáselmélet jóslatát. Egy későbbi mauritániai
napfogyatkozás során (1973-ban) a (1+
= 0. Az általános relativitáselmélet első kísérleti
igazolását 1919-ben végezték el egy teljes napfogyatkozás
alkalmával. Ezek a mérések meglehetősen pontatlanok
voltak, de mintegy harminc százalékos hibán belül
igazolták a relativitáselmélet jóslatát. Egy későbbi mauritániai
napfogyatkozás során (1973-ban) a (1+ 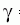 )/2 =
0,95
)/2 =
0,95 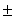 0,11 értéket mérték. 1967-ben Shapiro igen hosszú
alapvonalú módszerrel megmérte a 3C273 és a 3C279 jelű
kvazárok sugarainak elhajlását a napkorong közelében.
Ez a két pontszerű égi rádióforrás minden év október
8-án egészen közel kerül a Nap korongjához. A 3C279-et
rövid ideig el is takarja a Nap. A rádiócsillagászok 1969
óta ezen a napon minden évben megfigyelik a két kvazár
sugarainak elhajlását. Ez a két kvazárral történő differenciális
mérés csökkenti a légkör okozta
pontatlanságokat. További javaslatok a
pontosság növelésére:
0,11 értéket mérték. 1967-ben Shapiro igen hosszú
alapvonalú módszerrel megmérte a 3C273 és a 3C279 jelű
kvazárok sugarainak elhajlását a napkorong közelében.
Ez a két pontszerű égi rádióforrás minden év október
8-án egészen közel kerül a Nap korongjához. A 3C279-et
rövid ideig el is takarja a Nap. A rádiócsillagászok 1969
óta ezen a napon minden évben megfigyelik a két kvazár
sugarainak elhajlását. Ez a két kvazárral történő differenciális
mérés csökkenti a légkör okozta
pontatlanságokat. További javaslatok a
pontosság növelésére:
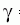 -paramétert szolgáltatja. A késés logaritmikusan
függ a Naptól mért szögtávolságtól. A Mariner-6, -7 és
-9 űrszondák megfigyelését használták az időkésés mérésére.
Egy másik módszer a Merkúr, Vénusz és Mars
felszínéről visszaverődő radarjelek mérése. Ha például
a Vénusz, a Nap és a Föld egy vonalban helyezkednek
el, a Vénuszról visszavert radarjelek összesen körülbelül
1000 másodpercig utaznak. Az általános relativitáselmélet
szerint a Nap gravitációs tere 0,0002 másodperccel
hosszabbítja meg ezeknek a hullámoknak a menetidejét.
A különféle gravitációelméletek szerint ez az időkésés
más és más értékű, de egyenesen arányos a fényelhajlás
értékével. A fényelhajlás és az időkésés mérésének
átlagolásával a (1+
-paramétert szolgáltatja. A késés logaritmikusan
függ a Naptól mért szögtávolságtól. A Mariner-6, -7 és
-9 űrszondák megfigyelését használták az időkésés mérésére.
Egy másik módszer a Merkúr, Vénusz és Mars
felszínéről visszaverődő radarjelek mérése. Ha például
a Vénusz, a Nap és a Föld egy vonalban helyezkednek
el, a Vénuszról visszavert radarjelek összesen körülbelül
1000 másodpercig utaznak. Az általános relativitáselmélet
szerint a Nap gravitációs tere 0,0002 másodperccel
hosszabbítja meg ezeknek a hullámoknak a menetidejét.
A különféle gravitációelméletek szerint ez az időkésés
más és más értékű, de egyenesen arányos a fényelhajlás
értékével. A fényelhajlás és az időkésés mérésének
átlagolásával a (1+ 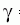 )/2= 0,993
)/2= 0,993 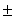 0,014 paraméterértéket
kapjuk.
Perihéliummozgás
A newtoni gravitációelméletben a bolygópályák önmagukba
visszatérő ellipszisek. Más metrikus gravitációelméletekben
a perihélium (a Naphoz legközelebbi pont)
keringésenként eltolódik. A különbséget a
0,014 paraméterértéket
kapjuk.
Perihéliummozgás
A newtoni gravitációelméletben a bolygópályák önmagukba
visszatérő ellipszisek. Más metrikus gravitációelméletekben
a perihélium (a Naphoz legközelebbi pont)
keringésenként eltolódik. A különbséget a 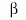 - és
- és 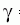 -paraméterek
mérik. A perihéliumpont szögsebességét a következőképpen
kapjuk a bolygópálya a fél nagytengelye
és e excentricitása segítségével:
-paraméterek
mérik. A perihéliumpont szögsebességét a következőképpen
kapjuk a bolygópálya a fél nagytengelye
és e excentricitása segítségével:
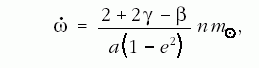
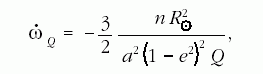
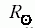 a Nap sugara. A kvadrupólmomentumot 1974-ben Hill és Stebbins mérte meg optikai úton [10]. A mért
lapultság 10,4
a Nap sugara. A kvadrupólmomentumot 1974-ben Hill és Stebbins mérte meg optikai úton [10]. A mért
lapultság 10,4 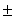 12,4 ezred ívmásodperc. Ennél pontosabb
mérés végezhető (10-8 relatív pontosság)perihélium mérésével
(Nordtvedt, Anderson és Colombo, 1977).
Gravitációs vöröseltolódás
A gravitációs vöröseltolódás a kibocsátott és elnyelt
elektromágneses rezgések frekvenciakülönbségében mutatkozik
meg. Ez az eltolódás akkor lép fel, ha a két pont
között a hullámok gravitációs potenciálban haladnak. A
vöröseltolódás a geometria görbültségét jellemzi (3.
táblázat ).
Az impulzusmomentum precessziója
A Föld körül keringő pörgettyű tengelye precessziós
mozgást végez annak következtében, hogy a Föld a tengelye
körül forog. A precesszió szögsebessége [11]:
12,4 ezred ívmásodperc. Ennél pontosabb
mérés végezhető (10-8 relatív pontosság)perihélium mérésével
(Nordtvedt, Anderson és Colombo, 1977).
Gravitációs vöröseltolódás
A gravitációs vöröseltolódás a kibocsátott és elnyelt
elektromágneses rezgések frekvenciakülönbségében mutatkozik
meg. Ez az eltolódás akkor lép fel, ha a két pont
között a hullámok gravitációs potenciálban haladnak. A
vöröseltolódás a geometria görbültségét jellemzi (3.
táblázat ).
Az impulzusmomentum precessziója
A Föld körül keringő pörgettyű tengelye precessziós
mozgást végez annak következtében, hogy a Föld a tengelye
körül forog. A precesszió szögsebessége [11]:
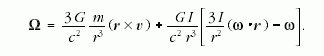
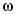 a Föld szögsebessége és I
a Föld tehetetlenségi nyomatéka. A jobb oldalon az első
tag a geodetikus precesszió. A mesterséges hold 500 km
magasságú sarki pályája esetén ez a tag 6,9 ívmásodperc/
év járulékot ad. A második tag a Lense-Thirringtag
[12] vagy tömegáramtag, amely erre a pályára 0,05
ívmásodperc/év. Ezt a kísérletet Leonard Schiff javasolta
45 évvel ezelőtt [13]. Mesterséges holdra a cseppfolyós
hélium hőmérsékletére hűtött pörgettyűket helyeznek
el. A négy pingponglabda nagyságú pörgettyűt olvasztott
kvarcból készítették el a skóciai Glasgowban.
Ezek a világ legpontosabb golyói. Felszínüket szupravezető
nióbiumréteg borítja. A pörgettyűk forgástengelyének
helyzetét a mágneses dipólmomentumuk (London-nyomaték)
segítségével mérik. A mágneses tér erősségét
10-7 Gaussra csökkentik le az erővonalak váltakozó fefúvása
és összeszorítása útján. A módszert van Kann és
Cabrera dolgozta ki. A műholdat sikeresen Föld körüli
pályára juttatták, és jelenleg folynak a tudományos mérések
előkészületei. Ennek során a műhold távcsövét a
Pegasus csillagkép egyik csillagára irányították rá, és 16
parányi rakéta segítségével ezt az irányt tartósan biztosítják.
A mérések egy éven át tartanak majd.
A fenti áttekintés alátámasztja, hogy a fizikai tudomány
- mint a természettudományok és a műszaki tudományok
általában - az ellenőrizhetőség és az áttekinthetőség
szilárd alapjára épül. Az érvek és a mérések mindenki
számára hozzáférhetők. Ez az átláthatóság teszi különösen
stabillá fizikai világképünket.
Irodalom
a Föld szögsebessége és I
a Föld tehetetlenségi nyomatéka. A jobb oldalon az első
tag a geodetikus precesszió. A mesterséges hold 500 km
magasságú sarki pályája esetén ez a tag 6,9 ívmásodperc/
év járulékot ad. A második tag a Lense-Thirringtag
[12] vagy tömegáramtag, amely erre a pályára 0,05
ívmásodperc/év. Ezt a kísérletet Leonard Schiff javasolta
45 évvel ezelőtt [13]. Mesterséges holdra a cseppfolyós
hélium hőmérsékletére hűtött pörgettyűket helyeznek
el. A négy pingponglabda nagyságú pörgettyűt olvasztott
kvarcból készítették el a skóciai Glasgowban.
Ezek a világ legpontosabb golyói. Felszínüket szupravezető
nióbiumréteg borítja. A pörgettyűk forgástengelyének
helyzetét a mágneses dipólmomentumuk (London-nyomaték)
segítségével mérik. A mágneses tér erősségét
10-7 Gaussra csökkentik le az erővonalak váltakozó fefúvása
és összeszorítása útján. A módszert van Kann és
Cabrera dolgozta ki. A műholdat sikeresen Föld körüli
pályára juttatták, és jelenleg folynak a tudományos mérések
előkészületei. Ennek során a műhold távcsövét a
Pegasus csillagkép egyik csillagára irányították rá, és 16
parányi rakéta segítségével ezt az irányt tartósan biztosítják.
A mérések egy éven át tartanak majd.
A fenti áttekintés alátámasztja, hogy a fizikai tudomány
- mint a természettudományok és a műszaki tudományok
általában - az ellenőrizhetőség és az áttekinthetőség
szilárd alapjára épül. Az érvek és a mérések mindenki
számára hozzáférhetők. Ez az átláthatóság teszi különösen
stabillá fizikai világképünket.
Irodalom