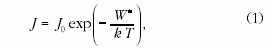
Fizikai Szemle honlap |
Tartalomjegyzék |
Gránásy László, Pusztai Tamás, Börzsönyi Tamás MTA SZFKI, Budapest
Legtöbb szerkezeti anyagunk polikristályos szerkezetű, azaz nagyszámú kristályszemcséből épül fel, amelyeknek méret, összetétel, alak stb. szerinti eloszlása, a mikroszerkezet határozza meg az adott anyag fizikai és korróziós tulajdonságait. A fémekkel kapcsolatos több ezer éves gyakorlat és a több mint száz évre visszatekintő tudományos vizsgálatok ellenére a polikristályos anyagok képződésének részletei csak kevéssé ismertek. A polikristályos anyagokat formálisan az alábbi két csoportba sorolhatjuk be: a) Anyagok, melyeket a nukleálódó és egymással ütköző egykristályok kölcsönhatása során létrejövő "habszerű" szemcsehatár-hálózat jellemez. Ez a mikroszerkezet a legtöbb anyagtudós jó ismerőse, minthogy gyakori jelenség az öntéssel létrehozott kristályos anyagokban. b) Polikristályos növekedési alakzatok, melyeknél új, eltérő kristálytani orientációjú szemcsék képződnek a megszilárdulási fronton. Az 1. ábra a polikristályos szerzetek morfológiai gazdagságát illusztrálja. Az egymással versengő nukleációval és növekedéssel létrejövő habszerű szemcsehatár-hálózat az 1.a ábrán látható. Polikristályos dendrites mintázat figyelhető meg az 1.b ábrán, mely elegendően hosszú idő után az 1.a ábrán látható alakzathoz hasonlóvá válhat. Polikristályos növekedési formák láthatók az 1.c-1.i ábrákon. A közelmúltban végzett kísérletek szerint kristályos szemcsék hozzáadásával az egykristály dendrites megszilárdulási forma polikristályos „szédelgő” dendritté alakítható (1.c ábra). Jellegzetes polikristályos növekedési mintázat a műanyag bevásárlószatyrok anyagában is megtalálható szferolit (1.d ábra). Ez az alakzat az anyagok meglehetősen széles körében figyelhető meg, többek között elemi szelénben (Se), noduláris öntöttvasban és különféle ásványokban is. Egyes esetekben a szferolitok képződése a két végén szétterülő kristálykévék (1.e ábra) létrejöttével kezdődik, melyek aztán ke- vésbé térkitöltő, virágszerű mintázatokká fejlődhetnek (lásd 1.f és 1.g ábrák). Közel merőleges elágazás esetén úgynevezett kvadritok jönnek létre (1.h ábra). A rendezetlen polikristályos növekedés gyakran fraktálszerű, ágas-bogas szerkezetekre vezet (1.i ábra). Bár az 1. ábrán látható bonyolult alakzatokat létrehozó mikrofolyamatok általában kevéssé ismertek, a kristálycsíra-képződés (kristálynukleáció ), a diffúziós instabilitások, a kristályszimmetriák és az idegen részecskék várhatóan fontos szerepet játszanak létrejöttükben.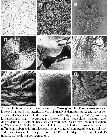 A polikristályos megszilárdulás leírásához
tehát olyan elméletre van szükség, amely alkalmas
mind a kristálycsíra-képződés, mind a
kristálynövekedés leírására. A modern statisztikus
fizikai módszerek és a rohamosan növekvő
számítástechnikai kapacitás kombinációjával
korábban megoldhatatlannak tűnő problémákra
találhatunk megoldást. Az elmúlt évtized
tapasztalatai alapján a fázismező-elmélet
(phase field theory ) a számítógépes anyagtudomány
egyik leghatékonyabb módszerének
bizonyult [1, 2]. Ebben az egyszerű, klasszikus
térelméleti modellben a kristály-folyadék átmenetet
a lokális fázisállapotot jellemző
A polikristályos megszilárdulás leírásához
tehát olyan elméletre van szükség, amely alkalmas
mind a kristálycsíra-képződés, mind a
kristálynövekedés leírására. A modern statisztikus
fizikai módszerek és a rohamosan növekvő
számítástechnikai kapacitás kombinációjával
korábban megoldhatatlannak tűnő problémákra
találhatunk megoldást. Az elmúlt évtized
tapasztalatai alapján a fázismező-elmélet
(phase field theory ) a számítógépes anyagtudomány
egyik leghatékonyabb módszerének
bizonyult [1, 2]. Ebben az egyszerű, klasszikus
térelméleti modellben a kristály-folyadék átmenetet
a lokális fázisállapotot jellemző
 fázismező írja le, melynek időfejlődése más,
lassan változó mezők (pl. összetétel, hőmérséklet,
orientáció) időfejlődéséhez csatolódik.
fázismező írja le, melynek időfejlődése más,
lassan változó mezők (pl. összetétel, hőmérséklet,
orientáció) időfejlődéséhez csatolódik.
 A továbbiakban azt vizsgáljuk, hogy ez a
modell alkalmas-e a kristálycsíra-képződés, illetve
polikristályos megszilárdulás leírására. Ennek
kapcsán összefoglaljuk a kristálynukleáció és polikristályos
megszilárdulás térelméleti modellezése területén
elért legújabb eredményeinket [3-7]. Olyan bonyolult jelenségeket
tárgyalunk, mint az eltérő kristálytani orientációjú
kristályszemcsék képződése és egymással versengő
növekedése, illetve komplex polikristályos megszilárdulási
mintázatok képződése. Ez utóbbi keretében a rendezetlen
("szédelgő") dendritek, szferolitok és fraktálszerű polikristályos
aggregátumok kialakulását vizsgáljuk. Végül olyan
idegen anyag ("fal") jelenlétében zajló folyamatokat modellezünk,
mint a heterogén nukleáció, idegen részecskék
és a kristályosodási front kölcsönhatása, illetve korlátozott
térben (csatornákban, ill. porózus közegekben) végbemenő
fagyás. Mielőtt a fázismező-elméleti eredmények ismertetését
megkezdenénk, felidézünk néhány, a polikristályos
megszilárdulás alapvető folyamataival, a nukleációval és
kristálynövekedéssel kapcsolatos eredményt.
A továbbiakban azt vizsgáljuk, hogy ez a
modell alkalmas-e a kristálycsíra-képződés, illetve
polikristályos megszilárdulás leírására. Ennek
kapcsán összefoglaljuk a kristálynukleáció és polikristályos
megszilárdulás térelméleti modellezése területén
elért legújabb eredményeinket [3-7]. Olyan bonyolult jelenségeket
tárgyalunk, mint az eltérő kristálytani orientációjú
kristályszemcsék képződése és egymással versengő
növekedése, illetve komplex polikristályos megszilárdulási
mintázatok képződése. Ez utóbbi keretében a rendezetlen
("szédelgő") dendritek, szferolitok és fraktálszerű polikristályos
aggregátumok kialakulását vizsgáljuk. Végül olyan
idegen anyag ("fal") jelenlétében zajló folyamatokat modellezünk,
mint a heterogén nukleáció, idegen részecskék
és a kristályosodási front kölcsönhatása, illetve korlátozott
térben (csatornákban, ill. porózus közegekben) végbemenő
fagyás. Mielőtt a fázismező-elméleti eredmények ismertetését
megkezdenénk, felidézünk néhány, a polikristályos
megszilárdulás alapvető folyamataival, a nukleációval és
kristálynövekedéssel kapcsolatos eredményt.
 Kristálycsíra-képződés
Az olvadáspontjuk alá hűtött homogén folyadékok fagyása
heterofázisú fluktuációk véletlen kialakulásával kezdődik,
melyek belsejében a kristályoshoz hasonló atomi rend figyelhető
meg (2. ábra) [8-11]. A heterofázisú fluktuációk
szabadenergiája durván két részre bontható, egy negatív
térfogati és egy pozitív felületi tagra. Kis méreteknél az
utóbbi dominál, így a heterofázisú fluktuációk szabadenergiája
maximumot mutat a méret függvényében. A maximumnak
a kritikus fluktuáció vagy nukleusz felel meg,
melynek képződési szabadenergiája W* . Azok a
fluktuációk, melyek nagyobbak ennél a kritikus méretnél, jó
eséllyel tovább növekednek, míg a kisebbek nagy valószínűséggel
elbomlanak. Másképp fogalmazva, a kristályos fázis
megjelenéséhez a rendszernek véletlen fluktuációkkal át
kell jutnia egy termodinamikai gáton. Ez a folyamat a kristálycsíra-
képződés, vagy más néven kristálynukleáció. Az
emberi időskálán zajló kristályosodási folyamatok esetén a
kritikus fluktuációk néhányszor tíz - néhányszor száz molekulát
tartalmaznak. Minthogy a kristály-folyadék határréteg
vastagsága néhány molekulaátmérő (3. ábra) [12], a
kritikus fluktuációk lényegében csak határrétegből állnak.
A nukleáció sebessége (egységnyi idő alatt, egységnyi térfogatban
képződő kritikus fluktuációk száma) a kritikus
fluktuáció szabadenergiájával hozható kapcsolatba:
Kristálycsíra-képződés
Az olvadáspontjuk alá hűtött homogén folyadékok fagyása
heterofázisú fluktuációk véletlen kialakulásával kezdődik,
melyek belsejében a kristályoshoz hasonló atomi rend figyelhető
meg (2. ábra) [8-11]. A heterofázisú fluktuációk
szabadenergiája durván két részre bontható, egy negatív
térfogati és egy pozitív felületi tagra. Kis méreteknél az
utóbbi dominál, így a heterofázisú fluktuációk szabadenergiája
maximumot mutat a méret függvényében. A maximumnak
a kritikus fluktuáció vagy nukleusz felel meg,
melynek képződési szabadenergiája W* . Azok a
fluktuációk, melyek nagyobbak ennél a kritikus méretnél, jó
eséllyel tovább növekednek, míg a kisebbek nagy valószínűséggel
elbomlanak. Másképp fogalmazva, a kristályos fázis
megjelenéséhez a rendszernek véletlen fluktuációkkal át
kell jutnia egy termodinamikai gáton. Ez a folyamat a kristálycsíra-
képződés, vagy más néven kristálynukleáció. Az
emberi időskálán zajló kristályosodási folyamatok esetén a
kritikus fluktuációk néhányszor tíz - néhányszor száz molekulát
tartalmaznak. Minthogy a kristály-folyadék határréteg
vastagsága néhány molekulaátmérő (3. ábra) [12], a
kritikus fluktuációk lényegében csak határrétegből állnak.
A nukleáció sebessége (egységnyi idő alatt, egységnyi térfogatban
képződő kritikus fluktuációk száma) a kritikus
fluktuáció szabadenergiájával hozható kapcsolatba:
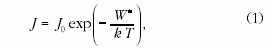
 A nukleációt követően a kristályszemcse növekedésnek
indul. Amennyiben a növekedést termikus vagy kémiai
diffúzió kontrollálja, a növekedés fokozatosan lassul a
megszilárdulási front előtt felhalmozódó hő vagy a folyadékfázisban
feldúsuló komponens miatt. Ez az állapot
azonban instabil a felületi fluktuációkkal szemben (Mullins
-Sekerka-instabilitás): egy kidudorodás például nagyobb
térszögben adja le a hőt (4. ábra), így gyorsabb
növekedésre van módja. Ennek megfelelően diffúziókontrollált
ujjasodás lép fel - amely a felületi szabadenergia
és/vagy a molekulák szilárd fázishoz való csatlakozását
leíró kinetikus együttható anizotrópiája miatt jól meghatározott
kristálytani irányokban történik - és ez dendrites
szerkezet kialakulására vezet (4. ábra). A fázismezőelmélet
egyik látványos sikere ezen bonyolult szerkezet
kialakulásának pontos leírása [2] (4. ábra).
A fázismező-elmélet
Anélkül, hogy teljességre törekednénk, a továbbiakban
röviden körvonalazzuk a fázismező-elmélet néhány alapvető
vonását. Az érdeklődők részletesebb képet kaphatnak
az [1, 2] irodalmi összefoglalókból. A fázismező-modell
olyan fenomenologikus térelméleti leírás, melyben
az anyag lokális állapotát több rendparaméter segítségével
jellemezzük. Ezek olyan lokálisan átlagolt fizikai tulajdonságok,
melyek lényegesen eltérnek a két fázisban, és
segítségükkel a szabadenergia kifejezhető. A kristályfolyadék
átmenetet a
A nukleációt követően a kristályszemcse növekedésnek
indul. Amennyiben a növekedést termikus vagy kémiai
diffúzió kontrollálja, a növekedés fokozatosan lassul a
megszilárdulási front előtt felhalmozódó hő vagy a folyadékfázisban
feldúsuló komponens miatt. Ez az állapot
azonban instabil a felületi fluktuációkkal szemben (Mullins
-Sekerka-instabilitás): egy kidudorodás például nagyobb
térszögben adja le a hőt (4. ábra), így gyorsabb
növekedésre van módja. Ennek megfelelően diffúziókontrollált
ujjasodás lép fel - amely a felületi szabadenergia
és/vagy a molekulák szilárd fázishoz való csatlakozását
leíró kinetikus együttható anizotrópiája miatt jól meghatározott
kristálytani irányokban történik - és ez dendrites
szerkezet kialakulására vezet (4. ábra). A fázismezőelmélet
egyik látványos sikere ezen bonyolult szerkezet
kialakulásának pontos leírása [2] (4. ábra).
A fázismező-elmélet
Anélkül, hogy teljességre törekednénk, a továbbiakban
röviden körvonalazzuk a fázismező-elmélet néhány alapvető
vonását. Az érdeklődők részletesebb képet kaphatnak
az [1, 2] irodalmi összefoglalókból. A fázismező-modell
olyan fenomenologikus térelméleti leírás, melyben
az anyag lokális állapotát több rendparaméter segítségével
jellemezzük. Ezek olyan lokálisan átlagolt fizikai tulajdonságok,
melyek lényegesen eltérnek a két fázisban, és
segítségükkel a szabadenergia kifejezhető. A kristályfolyadék
átmenetet a 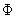 fázismező írja le, melynek értéke
egy és nulla között folyamatosan változik a kristály-folyadék
határfelületen keresztül.
fázismező írja le, melynek értéke
egy és nulla között folyamatosan változik a kristály-folyadék
határfelületen keresztül.
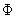 c. Fontos lokális jellemző
lehet a T hőmérséklet is. Többnyire azonban a termikus
kiegyenlítődés gyorsan végbemegy,
így jogos az állandó hőmérsékletű,
izoterm közelítés használata. Az inhomogén
kristályosodó folyadék szabadenergiáját
több tag összegeként írhatjuk
fel. Az egyik a fázismező térbeli
változásához rendelhető többlet szabadenergia
(ebből ered a felületi energia),
míg a második tag a lokális fázismező,
illetve összetétel értékekhez
tartozó szabadenergia. Ez utóbbi legalább
két minimummal rendelkezik,
melyek a makroszkopikusan megvalósuló
stabil és metastabil állapotoknak felelnek meg. A
túlhűtött folyadék kristályosodása esetén például a rendszer
a túlhűtött (metastabil) folyadékot jellemző lokális
minimumból a stabil kristályos fázist jellemző abszolút
minimumba kerül át, mely folyamat során át kell jutnia a
két minimum közt található szabadenergia-gáton. A rendszer
időbeli fejlődése a szabadenergia-felület alakjától (a
gát magasságától) és az atomi mozgékonyságtól függ. A
folyamatot leíró mozgásegyenletek erősen nemlineárisak,
meglehetősen bonyolultak, és megoldásukra csak a számítástechnika
utóbbi évtizedben tapasztalt látványos fejlődése
ad lehetőséget.
c. Fontos lokális jellemző
lehet a T hőmérséklet is. Többnyire azonban a termikus
kiegyenlítődés gyorsan végbemegy,
így jogos az állandó hőmérsékletű,
izoterm közelítés használata. Az inhomogén
kristályosodó folyadék szabadenergiáját
több tag összegeként írhatjuk
fel. Az egyik a fázismező térbeli
változásához rendelhető többlet szabadenergia
(ebből ered a felületi energia),
míg a második tag a lokális fázismező,
illetve összetétel értékekhez
tartozó szabadenergia. Ez utóbbi legalább
két minimummal rendelkezik,
melyek a makroszkopikusan megvalósuló
stabil és metastabil állapotoknak felelnek meg. A
túlhűtött folyadék kristályosodása esetén például a rendszer
a túlhűtött (metastabil) folyadékot jellemző lokális
minimumból a stabil kristályos fázist jellemző abszolút
minimumba kerül át, mely folyamat során át kell jutnia a
két minimum közt található szabadenergia-gáton. A rendszer
időbeli fejlődése a szabadenergia-felület alakjától (a
gát magasságától) és az atomi mozgékonyságtól függ. A
folyamatot leíró mozgásegyenletek erősen nemlineárisak,
meglehetősen bonyolultak, és megoldásukra csak a számítástechnika
utóbbi évtizedben tapasztalt látványos fejlődése
ad lehetőséget.
 A fenti probléma tovább bonyolódik, ha több kristály
egymással versengő növekedésének leírására van szükség,
ekkor ugyanis meg kell különböztetnünk a különféle
kristálytani orientációkat, azaz azt is meg kell adnunk,
hogy az egyes kristályszemcsék esetén a gyors növekedés
iránya milyen irányba mutat. Két dimenzióban ezt a Kobayashi,
Warren és Carter [13] által bevezetett újabb, úgynevezett
orientációs rendparaméter teszi lehetővé, amely
azt adja meg, hogy milyen irányban állnak a szerkezetet
jellemző kristálysíkok. Két eltérő orientációjú kristályszemcse
között kialakuló szemcsehatáron az orientációs
rendparaméter értéke élesen változik, amelyhez a javasolt
szabadenergia kifejezés extra energiát (a szemcsehatárenergia)
rendel. Kobayashi és munkatársai [13] csak a kristályban
értelmezték az orientációs rendparamétert. Valójában
azonban a kristályos rend és ennek részeként a kristályorientáció
is fokozatosan alakul ki a kristály-folyadék
határrétegben. A folyadék felé haladva "fellazul" a kristályos
rend és ennek részeként az orientációs rendezettség.
A folyadékbeli atomi mozgások számítógépes szimulációja
szerint, elsősorban geometriai megszorítások miatt, a
lokális atomi környezet (elsőszomszéd-környezet) még
egyszerű folyadékokban sem teljesen rendezetlen, hanem
többé-kevésbé hasonlít a kristályos elsőszomszéd-környezetre.
Így, ha megkeressük azt az irányt, melynél a tökéletes
kristályos környezet a legjobban hasonlít a vizsgált
folyadékatom elsőszomszéd-környezetére (a szögkorrelációt
vizsgáljuk), minden egyes folyadékatomhoz hozzárendelhetünk
egy pillanatnyi orientációt. Ez az orientáció
időben és térben ingadozik. Ugyanez az eljárás a kristályos
tartományokhoz jól meghatározott orientációt rendel.
A kristályosodási fronton áthaladva pedig a folyadékbeli
véletlenül ingadozó lokális orientáció fokozatosan beáll
az adott kristályszemcsére jellemző rögzített irányba. Ha
alacsony szimmetriájú (kevéssé szimmetrikus) molekulájú
folyadékkal van dolgunk, az orientációs rendparaméter a
molekulák pillanatnyi lokális irányultságát adja meg. A
szabadenergia kifejezés harmadik összetevőjeként fellépő
orientációs szabadenergiát úgy választottuk meg, hogy az
hűen reprodukálja ezeket a jelenségeket. Az ebből a tagból
eredő orientációs mozgásegyenlet csak azokban a
tartományokban vezet rendeződésre, ahol a fázismező
eltér a folyadékra jellemző értéktől [3]. Az orientációs rend
kialakulásához időt az orientációs mozgékonyság határozza
meg. Ha ez a mozgékonyság alacsony, akkor gyors
megszilárdulás esetén nincs idő a tökéletes orientációs
rend kialakítására, s így orientációs hibák, szemcsehatárok
képződnek.
A fenti probléma tovább bonyolódik, ha több kristály
egymással versengő növekedésének leírására van szükség,
ekkor ugyanis meg kell különböztetnünk a különféle
kristálytani orientációkat, azaz azt is meg kell adnunk,
hogy az egyes kristályszemcsék esetén a gyors növekedés
iránya milyen irányba mutat. Két dimenzióban ezt a Kobayashi,
Warren és Carter [13] által bevezetett újabb, úgynevezett
orientációs rendparaméter teszi lehetővé, amely
azt adja meg, hogy milyen irányban állnak a szerkezetet
jellemző kristálysíkok. Két eltérő orientációjú kristályszemcse
között kialakuló szemcsehatáron az orientációs
rendparaméter értéke élesen változik, amelyhez a javasolt
szabadenergia kifejezés extra energiát (a szemcsehatárenergia)
rendel. Kobayashi és munkatársai [13] csak a kristályban
értelmezték az orientációs rendparamétert. Valójában
azonban a kristályos rend és ennek részeként a kristályorientáció
is fokozatosan alakul ki a kristály-folyadék
határrétegben. A folyadék felé haladva "fellazul" a kristályos
rend és ennek részeként az orientációs rendezettség.
A folyadékbeli atomi mozgások számítógépes szimulációja
szerint, elsősorban geometriai megszorítások miatt, a
lokális atomi környezet (elsőszomszéd-környezet) még
egyszerű folyadékokban sem teljesen rendezetlen, hanem
többé-kevésbé hasonlít a kristályos elsőszomszéd-környezetre.
Így, ha megkeressük azt az irányt, melynél a tökéletes
kristályos környezet a legjobban hasonlít a vizsgált
folyadékatom elsőszomszéd-környezetére (a szögkorrelációt
vizsgáljuk), minden egyes folyadékatomhoz hozzárendelhetünk
egy pillanatnyi orientációt. Ez az orientáció
időben és térben ingadozik. Ugyanez az eljárás a kristályos
tartományokhoz jól meghatározott orientációt rendel.
A kristályosodási fronton áthaladva pedig a folyadékbeli
véletlenül ingadozó lokális orientáció fokozatosan beáll
az adott kristályszemcsére jellemző rögzített irányba. Ha
alacsony szimmetriájú (kevéssé szimmetrikus) molekulájú
folyadékkal van dolgunk, az orientációs rendparaméter a
molekulák pillanatnyi lokális irányultságát adja meg. A
szabadenergia kifejezés harmadik összetevőjeként fellépő
orientációs szabadenergiát úgy választottuk meg, hogy az
hűen reprodukálja ezeket a jelenségeket. Az ebből a tagból
eredő orientációs mozgásegyenlet csak azokban a
tartományokban vezet rendeződésre, ahol a fázismező
eltér a folyadékra jellemző értéktől [3]. Az orientációs rend
kialakulásához időt az orientációs mozgékonyság határozza
meg. Ha ez a mozgékonyság alacsony, akkor gyors
megszilárdulás esetén nincs idő a tökéletes orientációs
rend kialakítására, s így orientációs hibák, szemcsehatárok
képződnek.
 Itt jegyezzük meg, hogy az orientációs mobilitás az
orientációs egyensúly kialakulásának időskáláját meghatározó
rotációs diffúziós állandóval arányos. Ezzel szemben
a növekedési sebességet meghatározó fázismezőmobilitás
a transzlációs diffúziós állandóval arányos.
Komplex folyadékokban alacsony hőmérsékleten a rotációs
diffúziós állandó jelentősen lecsökken a transzlációs
diffúziós állandóhoz képest. Ennek tulajdonítható a polikristályos
növekedési mintázatok megjelenése nagy túlhűtéseknél.
A fent említett a folyamatokban alapvető szerepet játszanak
a véletlen atomi mozgások. A nemegyensúlyi statisztikus
fizika elvei szerint az átlagos viselkedésre származtatott
mozgásegyenleteink determinisztikusak. A folyamatok
statisztikus jellegének figyelembevételéhez alkalmas
"zajt" (megfelelő eloszlású és amplitúdójú véletlen
számokat) adunk a mozgásegyenletekhez. Ez a zaj hozza
létre véletlen helyen, időben és orientációval a kritikus
méretű kristályszemcséket, melyek aztán a felületi energia
anizotrópiája és az anyag-, illetve energiatranszport instabilitásainak
megfelelően fejlődnek tovább. Az eltérő orientációjú
kristályszemcsék létrejöttének beépítésével egy
új világ tárul ki előttünk. Olyan bonyolult polikristályos
mintázatok leírása válik lehetővé, melyek modellezése
korábban elképzelhetetlennek tűnt [3-7].
Kristálycsíra-képződés a fázismező-elméletben
Itt jegyezzük meg, hogy az orientációs mobilitás az
orientációs egyensúly kialakulásának időskáláját meghatározó
rotációs diffúziós állandóval arányos. Ezzel szemben
a növekedési sebességet meghatározó fázismezőmobilitás
a transzlációs diffúziós állandóval arányos.
Komplex folyadékokban alacsony hőmérsékleten a rotációs
diffúziós állandó jelentősen lecsökken a transzlációs
diffúziós állandóhoz képest. Ennek tulajdonítható a polikristályos
növekedési mintázatok megjelenése nagy túlhűtéseknél.
A fent említett a folyamatokban alapvető szerepet játszanak
a véletlen atomi mozgások. A nemegyensúlyi statisztikus
fizika elvei szerint az átlagos viselkedésre származtatott
mozgásegyenleteink determinisztikusak. A folyamatok
statisztikus jellegének figyelembevételéhez alkalmas
"zajt" (megfelelő eloszlású és amplitúdójú véletlen
számokat) adunk a mozgásegyenletekhez. Ez a zaj hozza
létre véletlen helyen, időben és orientációval a kritikus
méretű kristályszemcséket, melyek aztán a felületi energia
anizotrópiája és az anyag-, illetve energiatranszport instabilitásainak
megfelelően fejlődnek tovább. Az eltérő orientációjú
kristályszemcsék létrejöttének beépítésével egy
új világ tárul ki előttünk. Olyan bonyolult polikristályos
mintázatok leírása válik lehetővé, melyek modellezése
korábban elképzelhetetlennek tűnt [3-7].
Kristálycsíra-képződés a fázismező-elméletben
 A komplex megszilárdulási morfológiák tárgyalása előtt
érdemes megvizsgálni, milyen pontosság várható ettől a
lényegében fenomenologikus leírástól. Minthogy a nukleációs
sebesség igen érzékeny az alkalmazott közelítésekre,
így a fázismező-elméletet a kritikus fluktuáció tulajdonságainak
közvetlen számításával teszteljük. A kritikus
fluktuáció instabil egyensúlyi állapotban van a környezetével,
ennek megfelelően a szabadenergia szélsőértékének
felel meg [3, 5], melyet az alábbi határfeltételek
mellett keressük. A távoltérben az olvadáspontja alá hűtött,
kiinduló folyadék található, míg a fluktuáció közepén,
szimmetriamegfontolások alapján, a térgradiensek
zéró értéket vesznek fel. Az egykomponensű határesetben
a szabadenergia-funkcionál mindössze két paramétert
tartalmaz. Amennyiben a felületi szabadenergia és a
határréteg vastagsága stabil egyensúlyban (ti. az olvadásponton)
ismert, akkor ez a két paraméter rögzíthető, és a
nemegyensúlyi állapothoz tartozó kritikus fluktuáció tulajdonságai,
beleértve a fluktuáció W* szabadenergiáját
is, illesztő paraméter nélkül határozhatók meg. Amennyiben
ezen a bemenő adatok mellett a nukleációs gát magassága
is ismert, az elmélet pontosságának közvetlen
ellenőrzésére nyílik mód. Az egyszerű folyadékokéhoz
hasonló viselkedést mutató keménygömb-rendszer esetén
ez a helyzet. A számítógépes szimulációk alapján a
határréteg tulajdonságai (vastagsága [12], ill. szabadenergiája
[14]) és a nukleációs gát magassága [11] egyaránt
nagy pontossággal ismertek.
A komplex megszilárdulási morfológiák tárgyalása előtt
érdemes megvizsgálni, milyen pontosság várható ettől a
lényegében fenomenologikus leírástól. Minthogy a nukleációs
sebesség igen érzékeny az alkalmazott közelítésekre,
így a fázismező-elméletet a kritikus fluktuáció tulajdonságainak
közvetlen számításával teszteljük. A kritikus
fluktuáció instabil egyensúlyi állapotban van a környezetével,
ennek megfelelően a szabadenergia szélsőértékének
felel meg [3, 5], melyet az alábbi határfeltételek
mellett keressük. A távoltérben az olvadáspontja alá hűtött,
kiinduló folyadék található, míg a fluktuáció közepén,
szimmetriamegfontolások alapján, a térgradiensek
zéró értéket vesznek fel. Az egykomponensű határesetben
a szabadenergia-funkcionál mindössze két paramétert
tartalmaz. Amennyiben a felületi szabadenergia és a
határréteg vastagsága stabil egyensúlyban (ti. az olvadásponton)
ismert, akkor ez a két paraméter rögzíthető, és a
nemegyensúlyi állapothoz tartozó kritikus fluktuáció tulajdonságai,
beleértve a fluktuáció W* szabadenergiáját
is, illesztő paraméter nélkül határozhatók meg. Amennyiben
ezen a bemenő adatok mellett a nukleációs gát magassága
is ismert, az elmélet pontosságának közvetlen
ellenőrzésére nyílik mód. Az egyszerű folyadékokéhoz
hasonló viselkedést mutató keménygömb-rendszer esetén
ez a helyzet. A számítógépes szimulációk alapján a
határréteg tulajdonságai (vastagsága [12], ill. szabadenergiája
[14]) és a nukleációs gát magassága [11] egyaránt
nagy pontossággal ismertek.
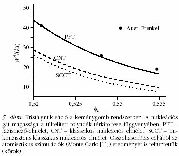
 Eredményeink arra utalnak, hogy a fázismező-elmélet
- illesztő paraméter nélkül - igen jól közelíti a számítógépes
szimulációkból adódó W* értékeket (5. ábra )
[5]. Ezzel szemben az anyagtudományban széles körben
alkalmazott klasszikus nukleációs elméletben használt
cseppmodell, amely éles határ és makroszkopikus termodinamikai
tulajdonságok feltételezésén alapul, lényegesen
alulbecsüli a nukleációs gát W* magasságát.
Ennek oka elsősorban az, hogy a határréteg vastagsága
összemérhető a kritikus fluktuáció
méretével, s így makroszkopikus kristálytulajdonságok
sehol sem figyelhetők
meg a kritikus fluktuáció belsejében
[5].
A mozgásegyenletekhez adott (termikus
fluktuációkat reprezentáló) numerikus
zaj segítségével a fázismezőelmélet
a nukleáció szimulálására is
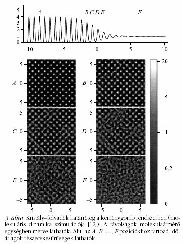
alkalmazható. A 6. ábrán látható pillanatfelvétel-
sorozat anizotróp rendszerben
történő kristálynukleációt mutat
be. Amint véletlen fluktuációval létrejön
egy szilárd tartomány a folyadékban,
azonnal megindul az orientációs
rendeződés. A végső kristálytani orientáció
akkor rögzül, amikor a kristályszemcse
elegendően naggyá válik ahhoz,
hogy a makroszkopikus kristálytulajdonságok
kialakuljanak. Ez az automatizmus lehetővé
teszi az 1.a és 1.b ábrán látható polikristályos megszilárdulási
morfológiák modellezését.
Polikristályos megszilárdulás: versengő
nukleáció és szemcsenövekedés
Az állandó nukleációs és növekedési sebesség esetén az
X kristályos hányad időfüggése a Johson-Mehl-Avrami-
Kolmogorov-skálázást követi:
Eredményeink arra utalnak, hogy a fázismező-elmélet
- illesztő paraméter nélkül - igen jól közelíti a számítógépes
szimulációkból adódó W* értékeket (5. ábra )
[5]. Ezzel szemben az anyagtudományban széles körben
alkalmazott klasszikus nukleációs elméletben használt
cseppmodell, amely éles határ és makroszkopikus termodinamikai
tulajdonságok feltételezésén alapul, lényegesen
alulbecsüli a nukleációs gát W* magasságát.
Ennek oka elsősorban az, hogy a határréteg vastagsága
összemérhető a kritikus fluktuáció
méretével, s így makroszkopikus kristálytulajdonságok
sehol sem figyelhetők
meg a kritikus fluktuáció belsejében
[5].
A mozgásegyenletekhez adott (termikus
fluktuációkat reprezentáló) numerikus
zaj segítségével a fázismezőelmélet
a nukleáció szimulálására is
alkalmazható. A 6. ábrán látható pillanatfelvétel-
sorozat anizotróp rendszerben
történő kristálynukleációt mutat
be. Amint véletlen fluktuációval létrejön
egy szilárd tartomány a folyadékban,
azonnal megindul az orientációs
rendeződés. A végső kristálytani orientáció
akkor rögzül, amikor a kristályszemcse
elegendően naggyá válik ahhoz,
hogy a makroszkopikus kristálytulajdonságok
kialakuljanak. Ez az automatizmus lehetővé
teszi az 1.a és 1.b ábrán látható polikristályos megszilárdulási
morfológiák modellezését.
Polikristályos megszilárdulás: versengő
nukleáció és szemcsenövekedés
Az állandó nukleációs és növekedési sebesség esetén az
X kristályos hányad időfüggése a Johson-Mehl-Avrami-
Kolmogorov-skálázást követi:
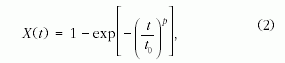
 Vizsgálataink szerint a dendritcsúcs csak akkor térül
el, ha pontosan eltalálja az idegen szemcsét, illetve ha az
idegen szemcse nagyobb, mint egy, a dendritcsúcs sugarával
összemérhető kritikus méret [4]. A kísérleti és fázismező-
szimulációs alakzatokat a 9. ábrán hasonlítjuk
össze. A kísérletek agyaggal adalékolt polimer rétegeken
történtek a National Institute of Standards and Technology
intézet Polimer Osztályán (Gaithersburg, Maryland,
USA). A szimulációkat nominálisan azonos körülmények
között, de különböző véletlen számokkal végeztük (az
MTA SZFKI-ban). A véletlen számok amplitúdója és szórása
azonos volt, csak a véletlenszám-generátor inicializálásában
tértek el. A bemutatott alakzatokat harminc szimuláció
közül a kísérleti mintázatokhoz való hasonlóság
alapján választottuk ki. Minthogy ezek az alakzatok a
természetben sem ismétlődnek meg, csak statisztikus
hasonlóság várható el kísérlet és elmélet között.
Vizsgálataink szerint a dendritcsúcs csak akkor térül
el, ha pontosan eltalálja az idegen szemcsét, illetve ha az
idegen szemcse nagyobb, mint egy, a dendritcsúcs sugarával
összemérhető kritikus méret [4]. A kísérleti és fázismező-
szimulációs alakzatokat a 9. ábrán hasonlítjuk
össze. A kísérletek agyaggal adalékolt polimer rétegeken
történtek a National Institute of Standards and Technology
intézet Polimer Osztályán (Gaithersburg, Maryland,
USA). A szimulációkat nominálisan azonos körülmények
között, de különböző véletlen számokkal végeztük (az
MTA SZFKI-ban). A véletlen számok amplitúdója és szórása
azonos volt, csak a véletlenszám-generátor inicializálásában
tértek el. A bemutatott alakzatokat harminc szimuláció
közül a kísérleti mintázatokhoz való hasonlóság
alapján választottuk ki. Minthogy ezek az alakzatok a
természetben sem ismétlődnek meg, csak statisztikus
hasonlóság várható el kísérlet és elmélet között.
 Az idegen részecskék számának növelésével egyre
rendezetlenebb alakzatok jönnek létre, és fokozatos átmenet
figyelhető meg a szabályos dendrites forma, a
"szédelgő" dendritek és a "moszatszerű" (seaweed) morfológia
között (10. ábra). Ez utóbbi általában az elhanyagolható
kristályanizotrópiával rendelkező rendszerekben
figyelhető meg. A dendrites megszilárdulásra képes, anizotróp
rendszerekben csak amiatt valósulhat meg, mivel
a nagyszámú, kisméretű szemcse anizotrópiájának hatása
kiátlagolódik a megszilárdulási front mentén [6].
Az idegen részecskék számának növelésével egyre
rendezetlenebb alakzatok jönnek létre, és fokozatos átmenet
figyelhető meg a szabályos dendrites forma, a
"szédelgő" dendritek és a "moszatszerű" (seaweed) morfológia
között (10. ábra). Ez utóbbi általában az elhanyagolható
kristályanizotrópiával rendelkező rendszerekben
figyelhető meg. A dendrites megszilárdulásra képes, anizotróp
rendszerekben csak amiatt valósulhat meg, mivel
a nagyszámú, kisméretű szemcse anizotrópiájának hatása
kiátlagolódik a megszilárdulási front mentén [6].
 Érdekes módon hasonló morfológiai átmenet megy
végbe akkor is, ha a rotációs diffúziós állandóval arányos
orientációs mobilitást csökkentjük (11. ábra). Ha az orientációs
mobilitás elég kicsi a fázismező mobilitásához
képest, akkor a rendszer nem képes egyazon orientációt
kialakítani a megszilárdulási front mentén, csupán lokális
rendeződés lehetséges, s így részleges orientációs rend
fagy be a kristályba (különféle lokális orientációk és a
köztük kialakuló szemcsehatárok). Ebben az esetben is a
csökkenő szemcseméret okozta kiátlagolódás felelős a
globálisan izotróp viselkedés megjelenéséért [6]. A sztatikus
(idegen szennyezők) és a dinamikus heterogenitások
(befagyott orientációs rendezetlenség) ezen dualitása
általános jelenségnek tűnik.
Érdekes módon hasonló morfológiai átmenet megy
végbe akkor is, ha a rotációs diffúziós állandóval arányos
orientációs mobilitást csökkentjük (11. ábra). Ha az orientációs
mobilitás elég kicsi a fázismező mobilitásához
képest, akkor a rendszer nem képes egyazon orientációt
kialakítani a megszilárdulási front mentén, csupán lokális
rendeződés lehetséges, s így részleges orientációs rend
fagy be a kristályba (különféle lokális orientációk és a
köztük kialakuló szemcsehatárok). Ebben az esetben is a
csökkenő szemcseméret okozta kiátlagolódás felelős a
globálisan izotróp viselkedés megjelenéséért [6]. A sztatikus
(idegen szennyezők) és a dinamikus heterogenitások
(befagyott orientációs rendezetlenség) ezen dualitása
általános jelenségnek tűnik.
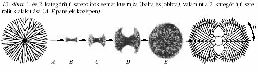 Hasonló okok felelősek az anizotrópia látszólagos
elvesztéséért a gyakorlatban használt anyagokban sűrűn
előforduló szferolitos növekedési forma esetén is (1.d
ábra). Érdemes megjegyezni, hogy szferolitnak nemcsak
a ténylegesen gömb alakú polikristályos alakzatokat szokás
nevezni, hanem azokat is, melyek lazább térkitöltésűek,
de az alakzat külső burkoló felülete gömbszerű. A
szferolitokat két csoportba osztják (12. ábra): Az 1. kategóriájú
szferolitok radiálisan megnyúlt formájú kristályszemcsékből
állnak össze, és fejlődésük minden fokozatában
gömbszerűek. Ezzel szemben a 2. kategóriájú szferolitok
kialakulásakor, egyetlen tukristály végeinek fokozatos,
többszöri elágazásával először legyezőszerűen
szétterülő végű kristálykéve alakul ki, majd további elágazással
gömbszerű (2 dimenzióban körszerű) alakzat jön
létre, melyben a kiinduló tűkristály körül gyakran egy
nem kristályos, gyűrű alakú csatorna (2 dimenzióban a
kezdeti tűkristály két oldalán nem kristályos "szemek")
figyelhető meg (12. ábra). Mindkét alakzattípus kialakulásában
alapvető szerepet játszik a tűkristályok krisztallográfiai
elágazása, melynek során az új ág meghatározott
krisztallográfiai irányban történő orientációváltással
és szemcsehatár kialakulásával jön létre (12. ábra).
Ennek a mechanizmusnak a modellezésére olyan orientációs
szabadenergia-tagot vezettünk be, amelynél az
állandó orientációjú növekedés
mellett egy második, metastabil
minimum is jelen van egy előre
meghatározott eltérülési szögnél.
Így a kristályoknak módjuk
nyílik adott szögben történő,
véletlen elágazásra. A metastabil
minimum mélysége és iránya,
valamint a felületi szabadenergia
és a fázismező-mobilitás anizotrópiájának
variálásával változatos, a kísérletekben is megvalósuló megszilárdulási
morfológiák modellezhetők (13. ábra).
Hasonló okok felelősek az anizotrópia látszólagos
elvesztéséért a gyakorlatban használt anyagokban sűrűn
előforduló szferolitos növekedési forma esetén is (1.d
ábra). Érdemes megjegyezni, hogy szferolitnak nemcsak
a ténylegesen gömb alakú polikristályos alakzatokat szokás
nevezni, hanem azokat is, melyek lazább térkitöltésűek,
de az alakzat külső burkoló felülete gömbszerű. A
szferolitokat két csoportba osztják (12. ábra): Az 1. kategóriájú
szferolitok radiálisan megnyúlt formájú kristályszemcsékből
állnak össze, és fejlődésük minden fokozatában
gömbszerűek. Ezzel szemben a 2. kategóriájú szferolitok
kialakulásakor, egyetlen tukristály végeinek fokozatos,
többszöri elágazásával először legyezőszerűen
szétterülő végű kristálykéve alakul ki, majd további elágazással
gömbszerű (2 dimenzióban körszerű) alakzat jön
létre, melyben a kiinduló tűkristály körül gyakran egy
nem kristályos, gyűrű alakú csatorna (2 dimenzióban a
kezdeti tűkristály két oldalán nem kristályos "szemek")
figyelhető meg (12. ábra). Mindkét alakzattípus kialakulásában
alapvető szerepet játszik a tűkristályok krisztallográfiai
elágazása, melynek során az új ág meghatározott
krisztallográfiai irányban történő orientációváltással
és szemcsehatár kialakulásával jön létre (12. ábra).
Ennek a mechanizmusnak a modellezésére olyan orientációs
szabadenergia-tagot vezettünk be, amelynél az
állandó orientációjú növekedés
mellett egy második, metastabil
minimum is jelen van egy előre
meghatározott eltérülési szögnél.
Így a kristályoknak módjuk
nyílik adott szögben történő,
véletlen elágazásra. A metastabil
minimum mélysége és iránya,
valamint a felületi szabadenergia
és a fázismező-mobilitás anizotrópiájának
variálásával változatos, a kísérletekben is megvalósuló megszilárdulási
morfológiák modellezhetők (13. ábra).
 Megszilárdulás fal jelenlétében
Amennyiben a falnál áramlásmentes ("no-flux") határfeltételt
írunk elő a fázismezőre (azaz, amikor a fázismező
gradiensének falra merőleges komponense eltűnik),
olyan egyszerű, éles határfelületű falat definiálhatunk
[15], melynél a kristály-folyadék határra vonatkoztatott
kontaktszög 90° (vagyis a kristály-folyadék határ derékszöget
zár be a fallal). Ezt az ötletet a kétalkotós, orientációs
mezővel kiegészített modellünkre adaptálva, olyan
kémiailag inert falat kapunk, melynek kristálytani orientációját
változtathatjuk. Az így definiált "falak" bevezetésével
az idegen részecskéken, durva felületeken történő
heterogén kristálynukleációt, illetve a korlátozott térrészekben
(porózus anyagban, csatornákban) végbemenő
fagyási folyamatokat vizsgálhatjuk
(14. ábra ).
Megszilárdulás fal jelenlétében
Amennyiben a falnál áramlásmentes ("no-flux") határfeltételt
írunk elő a fázismezőre (azaz, amikor a fázismező
gradiensének falra merőleges komponense eltűnik),
olyan egyszerű, éles határfelületű falat definiálhatunk
[15], melynél a kristály-folyadék határra vonatkoztatott
kontaktszög 90° (vagyis a kristály-folyadék határ derékszöget
zár be a fallal). Ezt az ötletet a kétalkotós, orientációs
mezővel kiegészített modellünkre adaptálva, olyan
kémiailag inert falat kapunk, melynek kristálytani orientációját
változtathatjuk. Az így definiált "falak" bevezetésével
az idegen részecskéken, durva felületeken történő
heterogén kristálynukleációt, illetve a korlátozott térrészekben
(porózus anyagban, csatornákban) végbemenő
fagyási folyamatokat vizsgálhatjuk
(14. ábra ).
 Számítástechnikai igény
Végül megjegyezzük, hogy a
fázismező-elméleti szimulációk
meglehetősen számításigényesek.
A megfelelő számítástechnikai
kapacitás biztosítására az
MTA SZFKI-ban felépítettünk
egy 76 PC-ből álló számítógépklasztert,
melynek további bővítése
folyamatban van. A 6., 7.,
9-11., 13. és 14. ábrán látható
szimulációk mindegyike ezen a
klaszteren készült.
Összefoglalás
A fázismező-elmélet általunk kifejlesztett
változata lehetőséget
nyújt a bonyolult polikristályos
megszilárdulási alakzatok leírá-
sára. A modell háromdimenziós kiterjesztése termodinamikai
adatbázisokkal, illetve hidrodinamikával összekombinálva
a számítógépes anyagtervezés egyik hatékony
eszközévé válhat. Ez azonban további komoly erőfeszítéseket
igényel.
Köszönetnyilvánítás
Köszönetet mondunk J.F. Douglasnak és V. Ferreironak a 8. és 9. ábrán
látható kísérleti felvételekért. Köszönet illeti amerikai társszerzőinket, J.A.
Warrent és J.F. Douglast a értékes diszkussziókért. A fenti vizsgálatok az
OTKA (T037323), valamint az ESA Prodex (14613/00/NL/SFe, 90109) és
ESA PECS (98005) programok támogatásával történtek. Pusztai Tamás
megköszöni a Bolyai János-ösztöndíj által nyújtott támogatást.
Irodalom
Számítástechnikai igény
Végül megjegyezzük, hogy a
fázismező-elméleti szimulációk
meglehetősen számításigényesek.
A megfelelő számítástechnikai
kapacitás biztosítására az
MTA SZFKI-ban felépítettünk
egy 76 PC-ből álló számítógépklasztert,
melynek további bővítése
folyamatban van. A 6., 7.,
9-11., 13. és 14. ábrán látható
szimulációk mindegyike ezen a
klaszteren készült.
Összefoglalás
A fázismező-elmélet általunk kifejlesztett
változata lehetőséget
nyújt a bonyolult polikristályos
megszilárdulási alakzatok leírá-
sára. A modell háromdimenziós kiterjesztése termodinamikai
adatbázisokkal, illetve hidrodinamikával összekombinálva
a számítógépes anyagtervezés egyik hatékony
eszközévé válhat. Ez azonban további komoly erőfeszítéseket
igényel.
Köszönetnyilvánítás
Köszönetet mondunk J.F. Douglasnak és V. Ferreironak a 8. és 9. ábrán
látható kísérleti felvételekért. Köszönet illeti amerikai társszerzőinket, J.A.
Warrent és J.F. Douglast a értékes diszkussziókért. A fenti vizsgálatok az
OTKA (T037323), valamint az ESA Prodex (14613/00/NL/SFe, 90109) és
ESA PECS (98005) programok támogatásával történtek. Pusztai Tamás
megköszöni a Bolyai János-ösztöndíj által nyújtott támogatást.
Irodalom