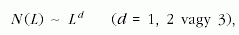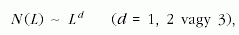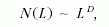Fizikai Szemle 2005/6. 221.o.
FRAKTÁLOK
Ha körülnézünk a szobánkban, elsőre csupa ismerős,
szabályos, "euklideszi" formát látunk: az asztal lábai
hasáb vagy henger alakúak, a teteje egy négyzet, vagy
téglalap, a kicsit komplikáltabb tárgyak, mint például egy
telefon vagy számítógép is néhány egyszerű forma kombinációjából
áll. Persze ha szemünk rátéved a falon függő
tájképre, már változik a helyzet, hiszen azon általában
mindenféle kusza, cizellált formák is előfordulnak: a felhők
pereme többnyire nagyon kacskaringós, és a bokrok,
fák, hegygerincek ábrázolásai is gazdag, szabálytalan
részleteket tartalmaznak.
Tehát az ember egyszerű, szabályos alakú tárgyakat
készít, de az élő és élettelen természetben tipikusan nem
szabályos, egyszerű formák fordulnak elő, hanem sokkal
jellemzőbb rájuk a sok kis részlet, az adott szabályszerűség
szerint ismétlődő mintázat. A komplikált alakzatok
geometriájának ugyanis megvannak a saját törvényei.
Döntő többségük önhasonló, ami azt jelenti, hogy egy kis
részletük közelről nézve olyan, mint az egész objektum.
Képzeljünk el egy tipikus, nagyméretű fakoronát,
ahogy az télen kinéz: nagyon bonyolult, hiszen sok ezer
kisebb-nagyobb ágat tartalmaz. Ha most képzeletben
kiragadjuk a fa valamelyik ágát, és éppen annyival nézzük
közelebbről, mint ahányszor kisebb, mint az eredeti
fa, akkor nagyjából (úgy mondjuk: statisztikai értelemben
véve) ugyanazt látjuk, mintha az eredeti fát néznénk. Ezt
a tulajdonságot hívjuk önhasonlóságnak, és a tipikus
fraktálok önhasonlóak. Ha ugyanezt valamilyen egyszerűbb
alakzattal próbáljuk megcsinálni, nagyon mást tapasztalunk.
Vegyünk például egy számot, a 8-at. "Középtávolságról"
egy értelmes jelet, magát a számot látjuk. Ha
kivágjuk egy részét, akkor vagy egy kis x-szerűséget,
vagy valamiféle görbe vonaldarabot kapunk. Aztán meg,
minél közelebbről nézzük (minél kisebb darabját vágjuk
ki), annál inkább kezd hasonlítani az, amit látunk, egy
egyenes vonaldarabkára. Ezeket azután hiába nagyítjuk
fel az eredeti 8-as méretére, az alakjuk teljesen más lesz.
A mellékelt képet ennek a cikknek az írása közben
készítettem (lementem az utcára és kerestem egy a célnak
megfelelő fát, majd egy képszerkesztővel kivágtam
és felnagyítottam belőle részeket), ezzel is próbálván
demonstrálni, hogy mennyire spontán módon kerülhetünk
kapcsolatba fraktálokkal, és győződhetünk meg
geometriájuk önhasonlóságáról.
Ha most a hagyományos eszközeinkkel jellemezni
akarnánk a fa geometriáját, és a burkolójára koncentrálnánk,
gömbszerűnek neveznénk, míg ha az ágacskákat
tartanánk jellemzőbbnek, akkor inkább a vonal fogalmát
használnánk, bár nyilvánvaló, hogy a valódi szerkezet
valahol a kettő között van. A gömb háromdimenziós, a
vonal egydimenziós, de hány dimenziós a fa koronája?
Képzeljük most el, hogy az alakzataink kis egységekből
állnak. Ha most összehasonlítjuk, hogy egy kétszer akkora
lineáris kiterjedésű vonalban hányszor több részecske
van, azt találjuk, hogy kétszer annyi. Egy kétszer akkora
kiterjedésű (átmérőjű) gömbben pedig nyolcszor annyi
részecske van, mert a közönséges objektumokban levő
részecskék száma N (L ) (tömegük, térfogatuk) a kiterjedésük
(L) egész számú hatványával nő:
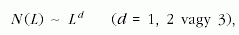
ahol ~ az arányosság jele. Ha azonban most elképzeljük,
hogy a fa koronájának egyre nagyobb kiterjedésű részeiben
határozzuk meg a "részecskék" számát (az ágakat úgy
tekinthetjük, mintha egységnyi térfogatú kis részekből állnának),
azt tapasztaljuk, hogy az így mért részecskeszámra
(tömegre, térfogatra) az alábbiösszefüggés áll fent:
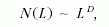
ahol D egy tört szám valahol 1 és 3 között. Ez a szám tört
(latinul fractio ), és az alakzat tömegének mérésére használt
formulánkban ott szerepel, ahol euklideszi alakzatokra
a közönséges dimenzió, ezért D-t fraktáldimenzió -
nak nevezzük. Egy fa jellegű, nagyon komplikált, önhasonló
alakzat dimenziója tehát tört szám. Ezt nehéz elképzelni,
de ugyanakkor ésszerűnek is tűnik. Az eredmény,
amit a dimenzióra kapunk, ugyanis valahol a vonalra
jellemző 1 és a gömbre vonatkozó 3 között van, és
valóban, ez igaz arra a benyomásra, amit a fa koronája
kelt bennünk.
Ha csak a fák és a felhők volnának fraktálszerkezetűek,
valószínűleg nem volna az érdeklődés olyan nagy az
ilyen fajta geometria iránt. Azonban számos olyan fizikai
és élővilágbeli folyamat van, amelyek fraktáltulajdonságai
meghatározóak a hétköznapjaink szempontjából is. Az
áramlásokkal és az általuk nagyban befolyásolt időjárással
kapcsolatos jelenségek számos törtdimenzójú struktúrát
generálnak. Elég a turbulens folyadékok által kirajzolt
komplex örvénymintázatokra vagy a rövid, de középtávon
is véletlenszerűen fluktuáló, rendkívül részletgazdag
hőmérsékletigrafi konokra gondolnunk. De a tőzsdei
árfolyamok ingadozása is fraktálgörbét rajzol ki.

De a fraktálok jelentőségét leginkább talán azzal lehet
érzékeltetni, hogy számba vesszük, hányféle fraktálalakzat
létezik mindannyiunk testében. A fák szerkezetéhez
hasonlít érhálózatunk, és sokszorosan elágazó nyúlványokkal
rendelkező idegsejtjeink is. A fraktáltulajdonság
az időben is megjelenik. Egy adott idegsejt pillanatszerű
elektromos impulzusokat produkál, úgy mondják, tüzel.
Megfigyelték, hogy ezeket az impulzusokat időben (tehát
egy vízszintes tengely mentén) ábrázolva fraktál ponthalmazt
rajzolnak ki.
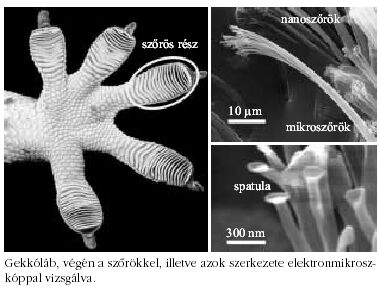
Egy nemrég felfedezett biológiai példával zárom a természetben
előforduló fraktálokra vonatkozó illusztrációk
sorát. Bizonyára sokan gondolják, hogy a gekkók azért
tudnak a falakon vagy függőleges üvegfelületen is szaladni,
mert a lábuk végén valamiféle szívókorongok vannak.
Valójában azonban másról van szó. A gekkók lábujjainak
végén amolyan mikroszkopikus fastruktúraként
több szinten át elágazó, a végső lépcsőben már nanométeres
tartományig vékonyuló bolyhok (ágacskák) vannak,
és ezek a mikroágacskák illeszkednek bele azokba a
mikroszkopikus hasadékokba, amelyek minden felületre
jellemzőek, hiszen - miért is lenne épp ez másképp -
megmutatható, hogy nagyon közelről nézve szinte minden
felület fraktálgeometriájú.
Vicsek Tamás
ELTE, Biológiai Fizika Tanszék