Fizikai Szemle 2006/2. 42.o.
AZ EROS KÖLCSÖNHATÁS FÁZISDIAGRAMJA
Fodor Zoltán
ELTE TTK Elméleti Fizika Tanszék
Az elemi részek fizikája a világ legkisebb és legalapvetőbb
építőelemeivel foglalkozik. A leggyakoribb vizsgálati
eljárás ezen részecskék ütköztetése valamely részecskegyorsítóban.
Ilyenkor néhány nagyenergiás részecske
vesz részt a folyamatban. Sokkal több nagyenergiás elemi
részecskével találkozhatunk bizonyos szélsőséges esetekben.
Ilyen például a korai Világegyetem, a neutroncsillagok
belseje vagy a nehézionok ütközése. Ezen fizikai folyamatok,
történések segítségével letapogathatjuk a részecskefizikai
elmélet fázisdiagramjának egyes részeit.
A jelenségkört leíró fizikai elmélet a kvantum-színdinamika,
az erős kölcsönhatás elmélete. Ez a kölcsönhatás
rendkívül erős. Töltéseinek szétválasztásakor az
elektromosságban szokásos 1/r típusú lecsengő potenciál
helyett egy minden határon túl növő lineáris potenciál
jelenik meg. Ez a tulajdonság felel azért, hogy a protonokban
található három kvark bezáródott. Közönséges
körülmények között nem nyílik lehetőség szabad kvarkok
észlelésére. Az energia növelésével a kölcsönhatás
gyengül. Ez fázisátmenethez vezethet, melynek során a
bezárt kvarkok kiszabadulnak. Ilyen nagy energiák jelennek
meg magas hőmérsékleten (ilyenkor az egy szabadsági
fokra jutó energia nagy) vagy nagy sűrűségek
esetén (ilyenkor a fermionok a Pauli-féle kizárási elv
miatt kerülnek egyre magasabb és magasabb energiaszintekre).
Egy rendszer fázisait a szokott módon a fázisdiagram
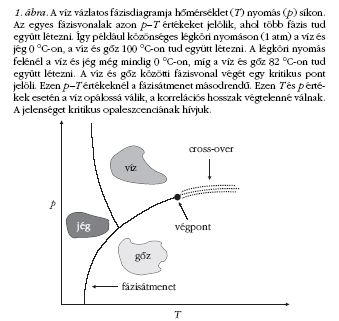
segítségével jellemezhetjük. Az 1. ábra sematikusan mutatja
a víz hétköznapi életben megjelenő fázisainak a hőmérséklet
és nyomás síkján felvett fázisdiagramját. A folytonos
vonalak elsőrendű fázisátmenetet mutatnak, míg a
pontozott rész az úgynevezett analitikus átmenet (crossover)
tartomány. A rendparaméternek tekinthető sűrűség
a cross-overen való áthaladáskor is gyorsan változik, de a
fázisátmenetekre jellemző szingularitás nem jelenik meg.
A fázisdiagram számunkra legfontosabb tulajdonsága a
kritikus "végpont" megjelenése. A víz 374 fokon és 0,32
kg/l sűrűségen opálossá válik, makroszkopikus méretű
korrelációk alakulnak ki. Érdemes megjegyezni, hogy ez
a fizikai állapot akár egy gázláng segítségével már megvalósítható
(bár a fellépő nagy nyomás miatt meglehetősen
erős tartályra van szükség).
A víz fázisdiagramja arra a kérdésre keresi a választ,
hogy mi történik a vízzel, ha egyre jobban melegítjük,
vagy egyre jobban összenyomjuk. A kérdést a részecskefizikában
sokkal általánosabban is feltehetjük. Mi történik
a "semmivel", a vákuummal, ha egyre jobban melegítjük?
Mi történik bármilyen anyaggal, ha egyre jobban összenyomjuk?
Ezekre a kérdésekre az erős kölcsönhatás ad választ.
Ez a kölcsönhatás, pontosabban ezen kölcsönhatásnak
egy legyengített, leárnyékolt fajtája felel a magerők nagyságáért,
az atombomba pusztító erejéért. A jelen írás célja
az erős kölcsönhatás fázisdiagramjának bemutatása.
A részecskefizika kölcsönhatásait (a már említett erős
kölcsönhatás mellett ilyen a radioaktív béta-bomlásért felelős
gyenge kölcsönhatás és a fotonokat leíró kvantumelektrodinamika)
a kvantum-mezőelméletek adják meg.
Ezen elméletek egyrészt mezőelméletek (más szóhasználattal
térelméletek), azaz a dinamikai változókat, mezőket
(más szóhasználattal tereket) a geometriai tér pontjaihoz
rendeljük. Ilyen klasszikus példa a meteorológia. A hőmérséklet,
nyomás, szélsebesség a tér különböző pontjaiban
más és más, és időben fejlődik. A kvantum-mezőelméletek
másik jellemzője, hogy kvantált elméletek. A legismertebb
példa a kvantált elméletekre a kvantummechanika, amelyben
a dinamikai változókat, az impulzust és a helyet nem
számokkal, hanem egymással fel nem cserélhető operátorokkal
jellemezzük. Ennek egyik jól ismert következménye
a Heisenberg-féle határozatlansági reláció, valamint az is,
hogy a test energiája nem lehet tetszőleges, hanem csak
bizonyos meghatározott érték. Az energia kvantált. A kvantum-
mezőelméletek ezen két fizikai leírási módötvözéséből
születtek. A dinamikai változók a mezők, melyeket a
meteorológiával ellentétben már nem számokkal, hanem
egymással fel nem cserélhető operátorokkal írunk le. Ezen
elmélet szerint is az energiaszintek meghatározottak, kvantáltak.
Ezen kvantumokhoz azonban már nemcsak meghatározott
energiát, hanem impulzust, impulzusmomentumot,
részecskeszámot is rendelhetünk. Kézenfekvő tehát a
gondolat, hogy az elemi részek fizikáját ezen részecskék,
ezen kvantumok segítségével írjuk le.
Rendkívül meglepő az a tény, hogy a fenti elképzelést
kiegészítve két, szinte triviális feltétellel az elemi részek
világának szinte minden jelensége nagy pontossággal leírható.
Ezen két feltétel egyike az önellentmondás-mentesség
(ezt minden végső elmélettől természetesen elvárjuk).
A másik feltétel, hogy az elmélet alapegyenleteit bizonyos
szimmetriatranszformációk változatlanul hagyják. A kvantum-
elektrodinamikában ez a transzformáció az anyagtereknek
egy egységnyi abszolút értékű komplex számmal
való megszorzása. A gyenge kölcsönhatás esetében a
szorzás 2×2-es (speciális unitér) mátrixokkal, az erős kölcsönhatás
esetében pedig 3×3-as (ugyancsak speciális
unitér) mátrixokkal történik. Szinte hihetetlen, hogy ezen
egyszerű transzformációk a kölcsönhatásokat egyértelműen
meghatározzák, és az eredmény teljes összhangban van
a kísérletekkel. Ennek szinte emblematikus példája az
elektron mágneses momentuma (annak a jellemzője, hogy
egy elektront mágneses mezőbe téve, majd a mező irányától
kissé eltérítve mekkora erők billentik vissza). Lenyűgöző,
hogy ezt a mennyiséget a kísérletek 12 tizedes jegyre
meg tudják határozni. Az elméleti fizikus számára talán
még lenyűgözőbb viszont az a tény, hogy a fenti egyszerű
elvek alapján - és persze sok fáradságos számolás után - a
kísérleti eredményekkel teljesen egyező elméleti jóslatot
tudunk adni. Ezek a számolások a perturbációszámítás
keretében történtek. Ezen eljárás a lényege az, hogy valamely
kis paraméter szerint hatványsorszerűen haladva fokozatosan
közelítjük az eredményt. Az elektron mágneses
momentumának pontos elméleti jóslata így azzal a ténnyel
magyarázható, hogy a számításban a kvantum-elektrodinamika
csatolási állandója, a finomszerkezeti állandó, 1/137
igen kicsi szám. Sajnos a perturbációszámítás, a fokozatos
közelítések módszere, nem mindig alkalmazható. Ha a
csatolási állandó nagy, akkor a perturbatív sortól nem várhatunk
konvergenciát. Az erős kölcsönhatás, ahogy neve is
mutatja, egy nagy csatolási állandót tartalmazó, erősen kölcsönható
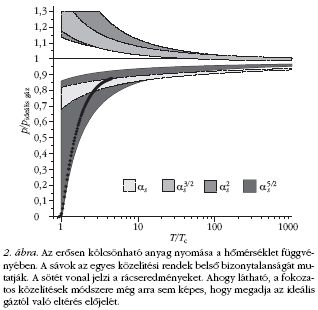
elmélet. A 2. ábra. mutatja az erősen kölcsönható
anyag nyomását a hőmérséklet függvényében (a nyomást
szokás az irodalomban az ideális gáz nyomásával normálni).
A vezető rendű eredmény mellett feltüntettük az azt
követő 3 további rendet is. A sort a finomszerkezeti állandóhoz
hasonló, erős csatolási állandó négyzetgyöke szerint
rendezzük. A sávok az egyes közelítési rendek belső bizonytalanságát
mutatják. A sötét vonal jelzi a nem perturbatív,
úgynevezett rácseredményeket. Ahogy látható, a
fokozatos közelítések módszere még arra sem képes, hogy
megadja az ideális gáztól való eltérés előjelét.
A probléma megoldása csak egy másik módszer, az
rácstérelmélet segítségével lehetséges. A rácstérelmélet a
teret és időt nem folytonos változókként kezeli, hanem
egy ráccsal helyettesíti. (Hasonló rácsot használnak az
időjárás-előrejelzés során, amikor különböző földrajzi
helyeken és magasságokban mérik a hőmérsékletet, szélirányt
és a nyomást. Minden polgári repülőgép elvégzi
repülés közben ezeket a méréseket, melyekből az adatok
összesítése és persze jelentős számolások után végül az
időjárás-előjelzések készülnek.) A részecskefizikában a
rács rácspontjaiba az elmélet mezőerősségeit írjuk. Láttuk,
hogy kvantumelméleteket egymással fel nem cserélhető
operátorok segítségével írhatunk le. Létezik egy másik
(Feynman Nobel-díjas amerikai kutató nevéhez fűződő)
pályaintegrálos leírási mód, mely jobban illeszkedik a
rácsformalizmushoz. A kvantummechanikai átmeneti
amplitúdót úgy határozzuk meg, hogy minden létező
klasszikus pályára összeadjuk az exp(iS ) fázisfaktorokat (i
a képzetes egységgyök, S az adott klasszikus pályához
tartozó hatás; érdemes megjegyezni, hogy klasszikus fizikában
egy pálya létezik, és ezt a hatás minimalizálása választja
ki). Igen egyszerű a fenti eljárást mezőelméletek
kvantálására használni. Ebben az esetben minden létező
mezőkonfigurációra adjuk össze az exp(iS ) fázisfaktorokat.
Mivel ezen fázisfaktorok igen erősen oszcillálnak,
célszerű a számolásokat euklideszi téridőben elvégezni. Itt
az idő formálisan a képzetes irányba halad, a fázisfaktorokból
pedig exp(-S ) alakú, a statisztikus fizikából jól
ismert, Boltzmann-faktorok lesznek. Ezen Boltzmann-faktorok
összegét euklideszi állapotösszegnek hívjuk.
Az egyes jelenségeket az állapotösszeg numerikus
meghatározásával, nagy számítógépekkel számítjuk ki.
Manapság 10 milliárd dimenziós integrálokat számolunk.
Másodpercenként ezermilliárd műveletre van szükség,
amely nyilván szuperszámítógépeknek való feladat.
Ilyen szuperszámítógép például a japán Earth Simulator,
Föld-számoló. Másodpercenként sok ezermilliárd
műveletet végez, de sajnos az ára is dollármilliárd nagyságrendű.
Magyarországon ez az út nem járható. Ezért az
ELTE-n kifejlesztettünk egy szuperszámítógépet, mely a
részecskefizikában versenyképes a japán géppel, de
annak töredékébe kerül. Ez annak tudható be, hogy mi
személyi számítógépekből építkezünk, és nem készen
vesszük a szuperszámítógépet. A személyi számítógépek
a számítási képességeikhez képest nagyon olcsók. Ez az
óriási piac miatt van. A hétköznapi életben a számítógépipar
egyik húzóereje a számítógépes játékok iránti igény.
Az ezekben megjelenő forgatás csoportja matematikai
értelemben nagyon hasonló (azzal lokálisan izomorf) a
standard részecskefizikai elmélet egyik szimmetriatranszformációjához.
Azaz, ameddig a személyi számítógépek
gyártói arra törekednek, hogy a játékprogramok minél
gyorsabban fussanak, és ennek megfelelően huzalozzák
be a processzorokat, addig a részecskefizikai számítások
is egyre gyorsabbak lesznek. Persze programozási szinten
el kell menni a megfelelő szintig.
A számítástechnika másik húzóereje az internet. Ma
már a gigabites hálózati kártya, gigabites hálózati kapcsoló
standardnak számít. De nem kell feltétlenül switchen
keresztül vinni az adatot. Ezért aztán feloszthatjuk a világegyetemet
apró részekre, ezeket számoljuk egy-egy
személyi számítógépen, és mindegyik részt összekötjük
egy gigabites kábel által a szomszédjával. Ezt megtehetjük,
hiszen a történések csak a közvetlen környezettől
függnek. Az ELTE személyi számítógépekből készített
egy szuperszámítógépet. 4 gigabites kártyát tettünk egy
gépbe, és mint egy kockás papíron, összekötöttük a négy
szomszédjával. Ilyen típusú számítógépek - melyet az
irodalomban Budapest-rendszernek neveztek el - ma
már a világ számos helyén működnek.
Térjünk vissza az erős kölcsönhatás elméletéhez, a
kvantum-színdinamikához (QCD). Mint minden elméletet,
ezt is a klasszikus Lagrange-függvénye révén célszerű
megadni. A klasszikus Lagrange-függvény ismeretében a
későbbiek során dől el, hogy egy elméletet klasszikus
elméletként kezelünk, vagy operátoros, illetve pályaintegrálos
módon kvantálunk-e.
A kvantum-színdinamikához nagyon hasonlít az elektrodinamika.
Az elektrodinamikában az elektromos és
mágneses mezőket, tereket (modern szóhasználattal a
mértéktereket) az A vektorpotenciál, az elektron terét
pedig egy 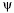 változó segítségével adjuk meg. A Lagrange-függvény
a következő, jól ismert módon írható fel.
változó segítségével adjuk meg. A Lagrange-függvény
a következő, jól ismert módon írható fel.
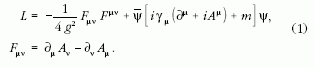
A fenti alakot a közismert mértékinvariancia lényegében
egyértelműen meghatározza. Mértékinvariancia alatt
azt értjük, hogy a Lagrange-függvény invariáns a mértéktranszformációkra.
Egy mértéktranszformáció során a
fermionteret egy helytől függő fázistényezővel szorozzuk,
a vektorpotenciálhoz pedig egy konstans szorzó
erejéig a fázis argumentumának a négyesdivergenciáját
adjuk. A Lagrange-függvény első tagja a mértéktag, mely
ebben az egyszerű ábeli esetben négyzetes 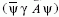 A második tag a fermiontag, melyben megjelenik a fermion-
mértékbozon kölcsönhatás. A Dirac-mátrixokat
A második tag a fermiontag, melyben megjelenik a fermion-
mértékbozon kölcsönhatás. A Dirac-mátrixokat 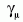 jelöli, míg a tömeget m.
Kézenfekvőnek tűnik a fenti Lagrange-függvény nemábeli
általánosítása. Ezen általánosítás során az A tér ne
egy valós szám legyen, hanem 2×2 (gyenge kölcsönhatás),
3×3 (erős kölcsönhatás) nulla átlósösszegű mátrix.
Ez az általánosítás értelemszerűen azt is jelenti, hogy a
fellépő A
jelöli, míg a tömeget m.
Kézenfekvőnek tűnik a fenti Lagrange-függvény nemábeli
általánosítása. Ezen általánosítás során az A tér ne
egy valós szám legyen, hanem 2×2 (gyenge kölcsönhatás),
3×3 (erős kölcsönhatás) nulla átlósösszegű mátrix.
Ez az általánosítás értelemszerűen azt is jelenti, hogy a
fellépő A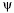 jellegű szorzatok miatt a
jellegű szorzatok miatt a
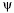 -nek a Dirac-indexen
felül 2 vagy 3 úgynevezett "színindexe" is van.
-nek a Dirac-indexen
felül 2 vagy 3 úgynevezett "színindexe" is van.
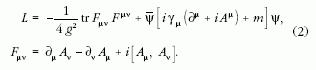
Hasonlóképpen az ábeli esethez (elektrodinamikához)
a mértékinvariancia a nem-ábeli esetben is lényegében
egyértelműen kijelöli ezt az alakot. Érdemes megjegyezni,
hogy az elektrodinamikával ellentétben a közvetítő
mező (A) önkölcsönhatásra képes, mely az utolsó tagban
jelenik meg: 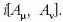 . Az ábeli esetben a mértékterek
valós számok, az ilyen kommutátor típusú tagok zérus
értéket vesznek fel. Nem-ábeli esetben az A tereket mátrixokkal
írjuk le, így a kommutátorok nemzérus értéket
vesznek fel.
Rácstérelméleti számolásokhoz az A tereket a rács élein,
fermionikus tereket a rács rácspontjain értelmezzük.
Az állapotösszeg a következő alakot veszi fel.
. Az ábeli esetben a mértékterek
valós számok, az ilyen kommutátor típusú tagok zérus
értéket vesznek fel. Nem-ábeli esetben az A tereket mátrixokkal
írjuk le, így a kommutátorok nemzérus értéket
vesznek fel.
Rácstérelméleti számolásokhoz az A tereket a rács élein,
fermionikus tereket a rács rácspontjain értelmezzük.
Az állapotösszeg a következő alakot veszi fel.
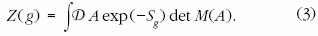
Az állapotösszegben a fent említett módon az összes
létező mértékkonfigurációra összegzünk. Ezt az összegzést
jelöltük formálisan 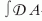 -val. A statisztikus fizikából A
jól ismert Boltzmann-faktor az exp(-Sg ) tag, ahol a Lagrange-
függvény első tagja, a mértéktag adja Sg-t. g a Lagrange-
függvényben is már szereplő csatolási állandó,
mellyel a későbbiek során a hőmérsékletet (T) fogjuk
változtatni; kis g magas, míg nagy g alacsony hőmérsékletet
jelent (ennek az az oka, hogy a rács fizikai mérete a
hőmérséklet reciprokával arányos, kis g kis rácsállandót,
így magas hőmérsékletet jelent). A g és T közötti egyértelmű
kapcsolat miatt a továbbiakban a számunkra fontosabb
T változót célszerű használni. A Lagrange-függvény
második, fermionikus tagra vonatkozó összegzése analitikusan
elvégezhető, és ez eredményezi detM(A)-t.
M(A)-t fermionmátrixnak nevezzük. Ez a mátrix a Lagrange-
függvény második tagjának diszkretizálásából származó
N×N mátrix, ahol N a rács pontjainak a száma. A
mátrix elemei a Lagrange-függvényből leolvashatók. A
-val. A statisztikus fizikából A
jól ismert Boltzmann-faktor az exp(-Sg ) tag, ahol a Lagrange-
függvény első tagja, a mértéktag adja Sg-t. g a Lagrange-
függvényben is már szereplő csatolási állandó,
mellyel a későbbiek során a hőmérsékletet (T) fogjuk
változtatni; kis g magas, míg nagy g alacsony hőmérsékletet
jelent (ennek az az oka, hogy a rács fizikai mérete a
hőmérséklet reciprokával arányos, kis g kis rácsállandót,
így magas hőmérsékletet jelent). A g és T közötti egyértelmű
kapcsolat miatt a továbbiakban a számunkra fontosabb
T változót célszerű használni. A Lagrange-függvény
második, fermionikus tagra vonatkozó összegzése analitikusan
elvégezhető, és ez eredményezi detM(A)-t.
M(A)-t fermionmátrixnak nevezzük. Ez a mátrix a Lagrange-
függvény második tagjának diszkretizálásából származó
N×N mátrix, ahol N a rács pontjainak a száma. A
mátrix elemei a Lagrange-függvényből leolvashatók. A
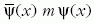 tag arra vezet, hogy a diagonális tagokban
a tömeg, m jelenik meg, míg a derivált tag a szomszédos
rácspontok között teremt kapcsolatot. A többi mátrixelem
eltűnik. Ezek alapján látható, hogy a mátrix igen ritka, a
diagonális és a diagonális melletti elemek kivételével
minden elem zérus.
A rácstérelmélettel mint módszerrel számos eredménye
ellenére volt egy megoldhatatlannak tűnő probléma.
Képes volt vákuumban, zérus anyagsűrűség mellett válaszokat
adni a kérdéseinkre, de sajnos egészen a közelmúltig
semmilyen eredményt nem kaptunk nemeltűnő
anyagsűrűség mellett (a fizikusok által használt pontosabb
név a véges barionsűrűség, barionoknak nevezzük
például a protont és a neutront). Ennek oka az elméleti
fizika számos területén fellépő úgynevezett előjelprobléma.
Zérus anyagsűrűség esetén a fizikai mennyiségek
kiszámításához szükséges állapotösszeg egyes tagjai
mind pozitívak. Nem eltűnő anyagsűrűség mellett az állapotösszegben
mind pozitív, mindnegatív tagok megjelennek,
melyek nagyrészt kölcsönösen kiejtik egymást.
Ennél is súlyosabb a negatív előjellel összefüggő következő
probléma. A rácstérelméletben fontossági mintavételt
alkalmazunk. Ennek során, az egyes mezőkonfigurációk
olyan valószínűséggel jelennek meg, mint amilyen
nagy az állapotösszegben a járulékuk. Ha azonban a járulék
negatív, akkor nem létezik hozzá tartozó valószínűség.
Ez a probléma minden fontossági mintavételen alapuló
eljárást lehetetlenné tesz. Ezért nem léteztek rácstérelméleti
eredmények nem eltűnő anyagsűrűség mellett.
Az elmúlt években ezen a területen robbanásszerű
változásnak lehettünk szemtanúi. Először az úgynevezett
többparaméteres átsúlyozás eljárásával sikerült erre a
fizikailag nagyon fontos kérdésre választ adni nem eltűnő
anyagsűrűség mellett, majd számos új módszer is megjelent
az irodalomban.
A nem eltűnő anyagsűrűséget fizikailag a jól ismert µ
kémiai potenciál segítségével vezetjük be. Minél nagyobb
µ, annál nagyobb az anyagsűrűség. A szokásos leírási
mód a nagy kanonikus állapotösszeg. A Lagrange-függvény
kiegészül a kémiai potenciál és az anyagsűrűség
szorzatát tartalmazó taggal, majd elvégezzük a mértéktérre
és a fermionikus terekre a szokásos összegzést. A már
említett, fermionikus tagra vonatkozó analitikusan elvégezhető
összegzés után megjelenő determináns így egy
µ-től függő tagot eredményez detM(A,µ ). Az állapotösszeg
így a következő alakot veszi fel:
tag arra vezet, hogy a diagonális tagokban
a tömeg, m jelenik meg, míg a derivált tag a szomszédos
rácspontok között teremt kapcsolatot. A többi mátrixelem
eltűnik. Ezek alapján látható, hogy a mátrix igen ritka, a
diagonális és a diagonális melletti elemek kivételével
minden elem zérus.
A rácstérelmélettel mint módszerrel számos eredménye
ellenére volt egy megoldhatatlannak tűnő probléma.
Képes volt vákuumban, zérus anyagsűrűség mellett válaszokat
adni a kérdéseinkre, de sajnos egészen a közelmúltig
semmilyen eredményt nem kaptunk nemeltűnő
anyagsűrűség mellett (a fizikusok által használt pontosabb
név a véges barionsűrűség, barionoknak nevezzük
például a protont és a neutront). Ennek oka az elméleti
fizika számos területén fellépő úgynevezett előjelprobléma.
Zérus anyagsűrűség esetén a fizikai mennyiségek
kiszámításához szükséges állapotösszeg egyes tagjai
mind pozitívak. Nem eltűnő anyagsűrűség mellett az állapotösszegben
mind pozitív, mindnegatív tagok megjelennek,
melyek nagyrészt kölcsönösen kiejtik egymást.
Ennél is súlyosabb a negatív előjellel összefüggő következő
probléma. A rácstérelméletben fontossági mintavételt
alkalmazunk. Ennek során, az egyes mezőkonfigurációk
olyan valószínűséggel jelennek meg, mint amilyen
nagy az állapotösszegben a járulékuk. Ha azonban a járulék
negatív, akkor nem létezik hozzá tartozó valószínűség.
Ez a probléma minden fontossági mintavételen alapuló
eljárást lehetetlenné tesz. Ezért nem léteztek rácstérelméleti
eredmények nem eltűnő anyagsűrűség mellett.
Az elmúlt években ezen a területen robbanásszerű
változásnak lehettünk szemtanúi. Először az úgynevezett
többparaméteres átsúlyozás eljárásával sikerült erre a
fizikailag nagyon fontos kérdésre választ adni nem eltűnő
anyagsűrűség mellett, majd számos új módszer is megjelent
az irodalomban.
A nem eltűnő anyagsűrűséget fizikailag a jól ismert µ
kémiai potenciál segítségével vezetjük be. Minél nagyobb
µ, annál nagyobb az anyagsűrűség. A szokásos leírási
mód a nagy kanonikus állapotösszeg. A Lagrange-függvény
kiegészül a kémiai potenciál és az anyagsűrűség
szorzatát tartalmazó taggal, majd elvégezzük a mértéktérre
és a fermionikus terekre a szokásos összegzést. A már
említett, fermionikus tagra vonatkozó analitikusan elvégezhető
összegzés után megjelenő determináns így egy
µ-től függő tagot eredményez detM(A,µ ). Az állapotösszeg
így a következő alakot veszi fel:
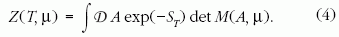
A fizikai kérdések megválaszolása szempontjából
rendkívül fontos az a tény, hogy detM(A,µ=0) mindig
pozitív valós szám, míg det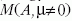 már nem az (a másik
tag, exp(-ST ) mindig pozitív valós). Ez a lehetséges
előjelváltozás vezet a már említett, híres előjelproblémára.
Zérus kémiai potenciálnál, egy adott mértékkonfiguráció
állapotösszegbeli járuléka exp(-ST)detM(A,µ=0)
pozitív valós szám, amelynek - adott normálási faktor
bevezetésével - 0 és 1 közötti valószínűségi értelmezést
adhatunk. Az állapotösszeg fontossági mintavételezésen
alapuló kiszámítási módja, ezt a valószínűségi értelmezést
használja ki, éppen ezzel a valószínűséggel veszi
bele az adott mértékkonfigurációt a mintába. Az állapotösszeget
néhány (általában ezer körüli), nagy súllyal
szereplő, így a mintavételezés során nagy valószínűséggel
megjelenő konfiguráció révén ki tudjuk számítani.
Drámaian megváltozik a helyzet nem zérus kémiai potenciál
esetében. Egy adott mértékkonfiguráció állapotösszegbeli
járuléka exp(-ST)det
már nem az (a másik
tag, exp(-ST ) mindig pozitív valós). Ez a lehetséges
előjelváltozás vezet a már említett, híres előjelproblémára.
Zérus kémiai potenciálnál, egy adott mértékkonfiguráció
állapotösszegbeli járuléka exp(-ST)detM(A,µ=0)
pozitív valós szám, amelynek - adott normálási faktor
bevezetésével - 0 és 1 közötti valószínűségi értelmezést
adhatunk. Az állapotösszeg fontossági mintavételezésen
alapuló kiszámítási módja, ezt a valószínűségi értelmezést
használja ki, éppen ezzel a valószínűséggel veszi
bele az adott mértékkonfigurációt a mintába. Az állapotösszeget
néhány (általában ezer körüli), nagy súllyal
szereplő, így a mintavételezés során nagy valószínűséggel
megjelenő konfiguráció révén ki tudjuk számítani.
Drámaian megváltozik a helyzet nem zérus kémiai potenciál
esetében. Egy adott mértékkonfiguráció állapotösszegbeli
járuléka exp(-ST)det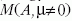 már nem pozitív
valós szám, így 0 és 1 közötti valószínűségi értelmezést
nem adhatunk neki. Ez egyben azt is jelenti, hogy a
valószínűségen alapuló fontossági mintavételezésre nincs
lehetőség. Ezen eljárás nélkül, az állapotösszeg közvetlen,
minden egyes térkonfigurációt felölelő kiszámítása
technikailag lehetetlen (az összeadandó tagok száma
olyan nagy, hogy ha az Univerzum minden egyes atomja
egy klasszikus számítógép lenne, amelyben fénysebességgel
mozgó elektronok számolnának, akkor sem lenne
elegendő a számítások elvégzéséhez a Világegyetem 15
milliárdéves teljes történelme).
A többparaméteres átsúlyozás módszere a következő
módon alakítja át az állapotösszeget.
már nem pozitív
valós szám, így 0 és 1 közötti valószínűségi értelmezést
nem adhatunk neki. Ez egyben azt is jelenti, hogy a
valószínűségen alapuló fontossági mintavételezésre nincs
lehetőség. Ezen eljárás nélkül, az állapotösszeg közvetlen,
minden egyes térkonfigurációt felölelő kiszámítása
technikailag lehetetlen (az összeadandó tagok száma
olyan nagy, hogy ha az Univerzum minden egyes atomja
egy klasszikus számítógép lenne, amelyben fénysebességgel
mozgó elektronok számolnának, akkor sem lenne
elegendő a számítások elvégzéséhez a Világegyetem 15
milliárdéves teljes történelme).
A többparaméteres átsúlyozás módszere a következő
módon alakítja át az állapotösszeget.
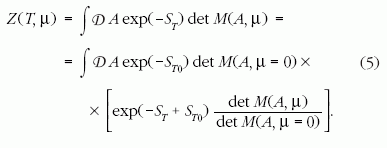
Ezen azonos átalakítás során bevezettük a T0 segédhőmérsékletet.
A fontossági mintavételezés T0 hőmérsékleten
és µ = 0 kémiai potenciál mellett történik (a
zérus kémiai potenciál nem vezet előjelproblémára). Ez
az átalakított állapotösszeg első két tényezője. A kifejezés
többi részét súlyként értelmezzük. Mivel ez a rész tartalmazza
detM(A,µ)-t, ezért a súly nem mindig pozitív. A
fontossági mintavételezés problémája megoldódott, az
elméletnek a váltakozó előjelekkel kapcsolatos tulajdonsága
pedig áthelyeződött egy oszcilláló súlyokból álló
összeg kiszámítására. Természetesen az eljárás működőképessége
azon múlik, hogy a fenti módon bevezetett
fontossági mintavételezés során (T0, µ = 0 paramétereknél)
valóban a vizsgálni kívánt elmélet ( 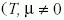 paramétereknél)
fontos konfigurációi jelennek-e meg.
Az irodalomban korábban használt úgynevezett Glasgow-
módszer mélyen a hadronikus fázisban gyűjtött
térkonfigurációkat. Ezeket a fenti módon súlyokkal látta
el, és így számította ki az állapotösszeget. Nyilvánvaló,
hogy a T tengelyen gyűjtött térkonfigurációk fizikai tartalma
teljesen más, mint a a fázishatár túloldalán lévő
fázist jellemző konfigurációké, ezért nem is várható,
hogy bármilyen információt szolgáltassanak a másik fázisról.
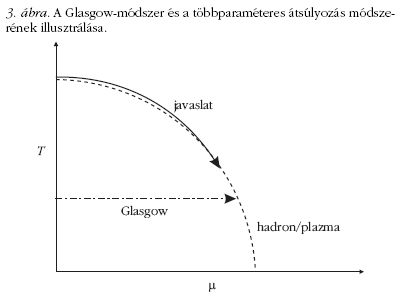
Ezért volt a Glasgow-módszer sikertelen. A többparaméteres
átsúlyozás magában a T tengelyen megjelenő
fázisátmeneti pontban gyűjt térkonfigurációkat. Mivel
ezen konfigurációk sokasága vegyesen tartalmazza a
két fázisra jellemző konfigurációkat, ezért kézenfekvőnek
tűnik, hogy ezeket lássuk el a megfelelő súlyokkal.
A fázishatár mentén átsúlyozva ki tudjuk elégíteni azt a
fizikai elvárást, hogy a fázisátmenet során a két fázis
együtt tudjon létezni. A két eljárás fizikai tartalmát a
3. ábra illusztrálja.
A fenti módszerrel lehetőség nyílt nemeltűnő kémiai
potenciál esetén is az erős kölcsönhatás vizsgálatára. Az
általunk vizsgálni kívánt fázisátmenet, matematikai értelemben
egy szingularitás, valójában véges térfogaton
soha nem jelenik meg, csak a végtelen térfogati határesetben.
paramétereknél)
fontos konfigurációi jelennek-e meg.
Az irodalomban korábban használt úgynevezett Glasgow-
módszer mélyen a hadronikus fázisban gyűjtött
térkonfigurációkat. Ezeket a fenti módon súlyokkal látta
el, és így számította ki az állapotösszeget. Nyilvánvaló,
hogy a T tengelyen gyűjtött térkonfigurációk fizikai tartalma
teljesen más, mint a a fázishatár túloldalán lévő
fázist jellemző konfigurációké, ezért nem is várható,
hogy bármilyen információt szolgáltassanak a másik fázisról.
Ezért volt a Glasgow-módszer sikertelen. A többparaméteres
átsúlyozás magában a T tengelyen megjelenő
fázisátmeneti pontban gyűjt térkonfigurációkat. Mivel
ezen konfigurációk sokasága vegyesen tartalmazza a
két fázisra jellemző konfigurációkat, ezért kézenfekvőnek
tűnik, hogy ezeket lássuk el a megfelelő súlyokkal.
A fázishatár mentén átsúlyozva ki tudjuk elégíteni azt a
fizikai elvárást, hogy a fázisátmenet során a két fázis
együtt tudjon létezni. A két eljárás fizikai tartalmát a
3. ábra illusztrálja.
A fenti módszerrel lehetőség nyílt nemeltűnő kémiai
potenciál esetén is az erős kölcsönhatás vizsgálatára. Az
általunk vizsgálni kívánt fázisátmenet, matematikai értelemben
egy szingularitás, valójában véges térfogaton
soha nem jelenik meg, csak a végtelen térfogati határesetben.
Célunk, az átmenet típusainak feltérképezése, a
fázisdiagram megadása a T-µ síkon, csak a térfogatfüggés
feltérképezésével valósítható meg. A fázisátmenetnek
megfelelő szingularitást végtelen térfogati limeszben az
állapotösszeg zérushelye jelzi (érdemes emlékeztetni arra
a tényre, hogy a például a nyomást logZ segítségével
adjuk meg). Véges térfogaton is megjelennek ilyen zérus-
helyek - Lee-Yang-zérók -, igaz ezek nem fizikai, komplex
hőmérsékletekhez tartoznak. Amennyiben végtelen
térfogati limeszben a rendszer valódi fázisátmeneteken
megy keresztül, akkor a Lee-Yang-zérók a térfogat növelésekor
ráhúzódnak a valós tengelyre. Amennyiben csak
egy gyors, de analitikus átmenettel állunk szemben,
akkor a Lee-Yang-zéróknak a végtelen térfogati limeszben
is lesz nem eltűnő képzetes részük, az átmenet analitikus
marad. A Lee-Yang-zérók képzetes részének vizsgálata
így lehetővé teszi a szingularitásra vezető fázisátmenet
és az analitikus átmenet megkülönböztetését.
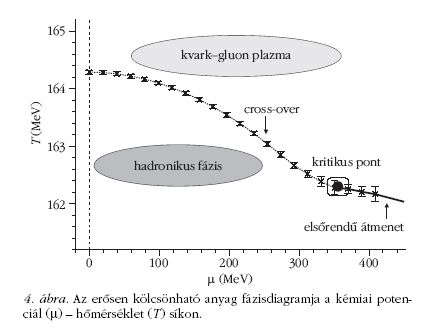
A 4. ábra mutatja a végeredményt. Két fázist különböztetünk
meg. Az alacsony hőmérsékletű fázist hadronikus
fázisnak nevezzük (ebben a fázisban a tipikus szabadsági
fokok a hadronok, kvarkokból és antikvarkokból
álló kötött részecskék). A magas hőmérsékletű fázist
kvark-gluon plazma fázisnak nevezzük (ebben a fázisban
a tipikus szabadsági fokok a kvarkok és gluonok). A
két állapot közötti átmenetet µ = 0 esetén az irodalom
részletesen tanulmányozta. Egészen a közelmúltig teljesen
ismeretlen volt viszont az átmenet függése az anyagsűrűségtől,
illetve az anyagsűrűség hangolására alkalmas
kémiai potenciáltól. Ahogy a 4. ábrán láthatjuk, zérus és
kis kémiai potenciál esetén a két fázis közötti átmenet
egy gyors cross-over. Egy adott hőmérséklet (kb. 162
MeV) és kémiai potenciál (kb. 360 MeV) esetén a fázisátmenet
másodrendű. A fázisdiagram ezen pontját hívjuk
kritikus végpontnak. Ebben a pontban a kritikus opaleszcenciához
hasonló jelenségek kísérleti megjelenését várjuk.
Ennél is nagyobb kémiai potenciál, illetve kisebb
hőmérséklet esetén a fázisátmenet elsőrendűvé válik.
A fázisdiagram kritikus pontjának tanulmányozása a
németországi GSI (Darmstadt) kutatóintézetben épülő új
részecskegyorsító egyik elsődleges célja.
Összefoglalva azt mondhatjuk, hogy az erős kölcsönhatás
segítségével adhatunk arra a kérdésre választ, hogy mi
történik bármilyen anyaggal, ha egyre jobban felmelegítjük,
illetve egyre jobban összenyomjuk. Egy új rácstérelméleti
módszer segítségével sikerült a fázisdiagram meghatározása,
melynek kísérleti ellenőrzése a közeljövő feladata.

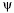 változó segítségével adjuk meg. A Lagrange-függvény
a következő, jól ismert módon írható fel.
változó segítségével adjuk meg. A Lagrange-függvény
a következő, jól ismert módon írható fel.
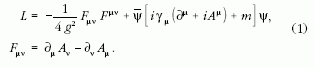
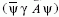 A második tag a fermiontag, melyben megjelenik a fermion-
mértékbozon kölcsönhatás. A Dirac-mátrixokat
A második tag a fermiontag, melyben megjelenik a fermion-
mértékbozon kölcsönhatás. A Dirac-mátrixokat 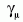 jelöli, míg a tömeget m.
Kézenfekvőnek tűnik a fenti Lagrange-függvény nemábeli
általánosítása. Ezen általánosítás során az A tér ne
egy valós szám legyen, hanem 2×2 (gyenge kölcsönhatás),
3×3 (erős kölcsönhatás) nulla átlósösszegű mátrix.
Ez az általánosítás értelemszerűen azt is jelenti, hogy a
fellépő A
jelöli, míg a tömeget m.
Kézenfekvőnek tűnik a fenti Lagrange-függvény nemábeli
általánosítása. Ezen általánosítás során az A tér ne
egy valós szám legyen, hanem 2×2 (gyenge kölcsönhatás),
3×3 (erős kölcsönhatás) nulla átlósösszegű mátrix.
Ez az általánosítás értelemszerűen azt is jelenti, hogy a
fellépő A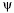 jellegű szorzatok miatt a
jellegű szorzatok miatt a
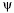 -nek a Dirac-indexen
felül 2 vagy 3 úgynevezett "színindexe" is van.
-nek a Dirac-indexen
felül 2 vagy 3 úgynevezett "színindexe" is van.
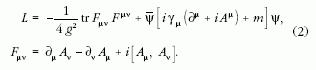
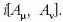 . Az ábeli esetben a mértékterek
valós számok, az ilyen kommutátor típusú tagok zérus
értéket vesznek fel. Nem-ábeli esetben az A tereket mátrixokkal
írjuk le, így a kommutátorok nemzérus értéket
vesznek fel.
Rácstérelméleti számolásokhoz az A tereket a rács élein,
fermionikus tereket a rács rácspontjain értelmezzük.
Az állapotösszeg a következő alakot veszi fel.
. Az ábeli esetben a mértékterek
valós számok, az ilyen kommutátor típusú tagok zérus
értéket vesznek fel. Nem-ábeli esetben az A tereket mátrixokkal
írjuk le, így a kommutátorok nemzérus értéket
vesznek fel.
Rácstérelméleti számolásokhoz az A tereket a rács élein,
fermionikus tereket a rács rácspontjain értelmezzük.
Az állapotösszeg a következő alakot veszi fel.
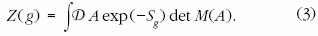
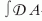 -val. A statisztikus fizikából A
jól ismert Boltzmann-faktor az exp(-Sg ) tag, ahol a Lagrange-
függvény első tagja, a mértéktag adja Sg-t. g a Lagrange-
függvényben is már szereplő csatolási állandó,
mellyel a későbbiek során a hőmérsékletet (T) fogjuk
változtatni; kis g magas, míg nagy g alacsony hőmérsékletet
jelent (ennek az az oka, hogy a rács fizikai mérete a
hőmérséklet reciprokával arányos, kis g kis rácsállandót,
így magas hőmérsékletet jelent). A g és T közötti egyértelmű
kapcsolat miatt a továbbiakban a számunkra fontosabb
T változót célszerű használni. A Lagrange-függvény
második, fermionikus tagra vonatkozó összegzése analitikusan
elvégezhető, és ez eredményezi detM(A)-t.
M(A)-t fermionmátrixnak nevezzük. Ez a mátrix a Lagrange-
függvény második tagjának diszkretizálásából származó
N×N mátrix, ahol N a rács pontjainak a száma. A
mátrix elemei a Lagrange-függvényből leolvashatók. A
-val. A statisztikus fizikából A
jól ismert Boltzmann-faktor az exp(-Sg ) tag, ahol a Lagrange-
függvény első tagja, a mértéktag adja Sg-t. g a Lagrange-
függvényben is már szereplő csatolási állandó,
mellyel a későbbiek során a hőmérsékletet (T) fogjuk
változtatni; kis g magas, míg nagy g alacsony hőmérsékletet
jelent (ennek az az oka, hogy a rács fizikai mérete a
hőmérséklet reciprokával arányos, kis g kis rácsállandót,
így magas hőmérsékletet jelent). A g és T közötti egyértelmű
kapcsolat miatt a továbbiakban a számunkra fontosabb
T változót célszerű használni. A Lagrange-függvény
második, fermionikus tagra vonatkozó összegzése analitikusan
elvégezhető, és ez eredményezi detM(A)-t.
M(A)-t fermionmátrixnak nevezzük. Ez a mátrix a Lagrange-
függvény második tagjának diszkretizálásából származó
N×N mátrix, ahol N a rács pontjainak a száma. A
mátrix elemei a Lagrange-függvényből leolvashatók. A
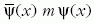 tag arra vezet, hogy a diagonális tagokban
a tömeg, m jelenik meg, míg a derivált tag a szomszédos
rácspontok között teremt kapcsolatot. A többi mátrixelem
eltűnik. Ezek alapján látható, hogy a mátrix igen ritka, a
diagonális és a diagonális melletti elemek kivételével
minden elem zérus.
A rácstérelmélettel mint módszerrel számos eredménye
ellenére volt egy megoldhatatlannak tűnő probléma.
Képes volt vákuumban, zérus anyagsűrűség mellett válaszokat
adni a kérdéseinkre, de sajnos egészen a közelmúltig
semmilyen eredményt nem kaptunk nemeltűnő
anyagsűrűség mellett (a fizikusok által használt pontosabb
név a véges barionsűrűség, barionoknak nevezzük
például a protont és a neutront). Ennek oka az elméleti
fizika számos területén fellépő úgynevezett előjelprobléma.
Zérus anyagsűrűség esetén a fizikai mennyiségek
kiszámításához szükséges állapotösszeg egyes tagjai
mind pozitívak. Nem eltűnő anyagsűrűség mellett az állapotösszegben
mind pozitív, mindnegatív tagok megjelennek,
melyek nagyrészt kölcsönösen kiejtik egymást.
Ennél is súlyosabb a negatív előjellel összefüggő következő
probléma. A rácstérelméletben fontossági mintavételt
alkalmazunk. Ennek során, az egyes mezőkonfigurációk
olyan valószínűséggel jelennek meg, mint amilyen
nagy az állapotösszegben a járulékuk. Ha azonban a járulék
negatív, akkor nem létezik hozzá tartozó valószínűség.
Ez a probléma minden fontossági mintavételen alapuló
eljárást lehetetlenné tesz. Ezért nem léteztek rácstérelméleti
eredmények nem eltűnő anyagsűrűség mellett.
Az elmúlt években ezen a területen robbanásszerű
változásnak lehettünk szemtanúi. Először az úgynevezett
többparaméteres átsúlyozás eljárásával sikerült erre a
fizikailag nagyon fontos kérdésre választ adni nem eltűnő
anyagsűrűség mellett, majd számos új módszer is megjelent
az irodalomban.
A nem eltűnő anyagsűrűséget fizikailag a jól ismert µ
kémiai potenciál segítségével vezetjük be. Minél nagyobb
µ, annál nagyobb az anyagsűrűség. A szokásos leírási
mód a nagy kanonikus állapotösszeg. A Lagrange-függvény
kiegészül a kémiai potenciál és az anyagsűrűség
szorzatát tartalmazó taggal, majd elvégezzük a mértéktérre
és a fermionikus terekre a szokásos összegzést. A már
említett, fermionikus tagra vonatkozó analitikusan elvégezhető
összegzés után megjelenő determináns így egy
µ-től függő tagot eredményez detM(A,µ ). Az állapotösszeg
így a következő alakot veszi fel:
tag arra vezet, hogy a diagonális tagokban
a tömeg, m jelenik meg, míg a derivált tag a szomszédos
rácspontok között teremt kapcsolatot. A többi mátrixelem
eltűnik. Ezek alapján látható, hogy a mátrix igen ritka, a
diagonális és a diagonális melletti elemek kivételével
minden elem zérus.
A rácstérelmélettel mint módszerrel számos eredménye
ellenére volt egy megoldhatatlannak tűnő probléma.
Képes volt vákuumban, zérus anyagsűrűség mellett válaszokat
adni a kérdéseinkre, de sajnos egészen a közelmúltig
semmilyen eredményt nem kaptunk nemeltűnő
anyagsűrűség mellett (a fizikusok által használt pontosabb
név a véges barionsűrűség, barionoknak nevezzük
például a protont és a neutront). Ennek oka az elméleti
fizika számos területén fellépő úgynevezett előjelprobléma.
Zérus anyagsűrűség esetén a fizikai mennyiségek
kiszámításához szükséges állapotösszeg egyes tagjai
mind pozitívak. Nem eltűnő anyagsűrűség mellett az állapotösszegben
mind pozitív, mindnegatív tagok megjelennek,
melyek nagyrészt kölcsönösen kiejtik egymást.
Ennél is súlyosabb a negatív előjellel összefüggő következő
probléma. A rácstérelméletben fontossági mintavételt
alkalmazunk. Ennek során, az egyes mezőkonfigurációk
olyan valószínűséggel jelennek meg, mint amilyen
nagy az állapotösszegben a járulékuk. Ha azonban a járulék
negatív, akkor nem létezik hozzá tartozó valószínűség.
Ez a probléma minden fontossági mintavételen alapuló
eljárást lehetetlenné tesz. Ezért nem léteztek rácstérelméleti
eredmények nem eltűnő anyagsűrűség mellett.
Az elmúlt években ezen a területen robbanásszerű
változásnak lehettünk szemtanúi. Először az úgynevezett
többparaméteres átsúlyozás eljárásával sikerült erre a
fizikailag nagyon fontos kérdésre választ adni nem eltűnő
anyagsűrűség mellett, majd számos új módszer is megjelent
az irodalomban.
A nem eltűnő anyagsűrűséget fizikailag a jól ismert µ
kémiai potenciál segítségével vezetjük be. Minél nagyobb
µ, annál nagyobb az anyagsűrűség. A szokásos leírási
mód a nagy kanonikus állapotösszeg. A Lagrange-függvény
kiegészül a kémiai potenciál és az anyagsűrűség
szorzatát tartalmazó taggal, majd elvégezzük a mértéktérre
és a fermionikus terekre a szokásos összegzést. A már
említett, fermionikus tagra vonatkozó analitikusan elvégezhető
összegzés után megjelenő determináns így egy
µ-től függő tagot eredményez detM(A,µ ). Az állapotösszeg
így a következő alakot veszi fel:
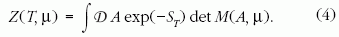
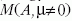 már nem az (a másik
tag, exp(-ST ) mindig pozitív valós). Ez a lehetséges
előjelváltozás vezet a már említett, híres előjelproblémára.
Zérus kémiai potenciálnál, egy adott mértékkonfiguráció
állapotösszegbeli járuléka exp(-ST)detM(A,µ=0)
pozitív valós szám, amelynek - adott normálási faktor
bevezetésével - 0 és 1 közötti valószínűségi értelmezést
adhatunk. Az állapotösszeg fontossági mintavételezésen
alapuló kiszámítási módja, ezt a valószínűségi értelmezést
használja ki, éppen ezzel a valószínűséggel veszi
bele az adott mértékkonfigurációt a mintába. Az állapotösszeget
néhány (általában ezer körüli), nagy súllyal
szereplő, így a mintavételezés során nagy valószínűséggel
megjelenő konfiguráció révén ki tudjuk számítani.
Drámaian megváltozik a helyzet nem zérus kémiai potenciál
esetében. Egy adott mértékkonfiguráció állapotösszegbeli
járuléka exp(-ST)det
már nem az (a másik
tag, exp(-ST ) mindig pozitív valós). Ez a lehetséges
előjelváltozás vezet a már említett, híres előjelproblémára.
Zérus kémiai potenciálnál, egy adott mértékkonfiguráció
állapotösszegbeli járuléka exp(-ST)detM(A,µ=0)
pozitív valós szám, amelynek - adott normálási faktor
bevezetésével - 0 és 1 közötti valószínűségi értelmezést
adhatunk. Az állapotösszeg fontossági mintavételezésen
alapuló kiszámítási módja, ezt a valószínűségi értelmezést
használja ki, éppen ezzel a valószínűséggel veszi
bele az adott mértékkonfigurációt a mintába. Az állapotösszeget
néhány (általában ezer körüli), nagy súllyal
szereplő, így a mintavételezés során nagy valószínűséggel
megjelenő konfiguráció révén ki tudjuk számítani.
Drámaian megváltozik a helyzet nem zérus kémiai potenciál
esetében. Egy adott mértékkonfiguráció állapotösszegbeli
járuléka exp(-ST)det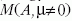 már nem pozitív
valós szám, így 0 és 1 közötti valószínűségi értelmezést
nem adhatunk neki. Ez egyben azt is jelenti, hogy a
valószínűségen alapuló fontossági mintavételezésre nincs
lehetőség. Ezen eljárás nélkül, az állapotösszeg közvetlen,
minden egyes térkonfigurációt felölelő kiszámítása
technikailag lehetetlen (az összeadandó tagok száma
olyan nagy, hogy ha az Univerzum minden egyes atomja
egy klasszikus számítógép lenne, amelyben fénysebességgel
mozgó elektronok számolnának, akkor sem lenne
elegendő a számítások elvégzéséhez a Világegyetem 15
milliárdéves teljes történelme).
A többparaméteres átsúlyozás módszere a következő
módon alakítja át az állapotösszeget.
már nem pozitív
valós szám, így 0 és 1 közötti valószínűségi értelmezést
nem adhatunk neki. Ez egyben azt is jelenti, hogy a
valószínűségen alapuló fontossági mintavételezésre nincs
lehetőség. Ezen eljárás nélkül, az állapotösszeg közvetlen,
minden egyes térkonfigurációt felölelő kiszámítása
technikailag lehetetlen (az összeadandó tagok száma
olyan nagy, hogy ha az Univerzum minden egyes atomja
egy klasszikus számítógép lenne, amelyben fénysebességgel
mozgó elektronok számolnának, akkor sem lenne
elegendő a számítások elvégzéséhez a Világegyetem 15
milliárdéves teljes történelme).
A többparaméteres átsúlyozás módszere a következő
módon alakítja át az állapotösszeget.
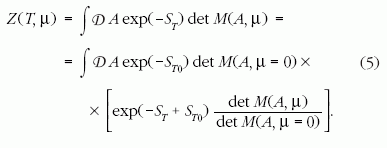
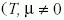 paramétereknél)
fontos konfigurációi jelennek-e meg.
Az irodalomban korábban használt úgynevezett Glasgow-
módszer mélyen a hadronikus fázisban gyűjtött
térkonfigurációkat. Ezeket a fenti módon súlyokkal látta
el, és így számította ki az állapotösszeget. Nyilvánvaló,
hogy a T tengelyen gyűjtött térkonfigurációk fizikai tartalma
teljesen más, mint a a fázishatár túloldalán lévő
fázist jellemző konfigurációké, ezért nem is várható,
hogy bármilyen információt szolgáltassanak a másik fázisról.
Ezért volt a Glasgow-módszer sikertelen. A többparaméteres
átsúlyozás magában a T tengelyen megjelenő
fázisátmeneti pontban gyűjt térkonfigurációkat. Mivel
ezen konfigurációk sokasága vegyesen tartalmazza a
két fázisra jellemző konfigurációkat, ezért kézenfekvőnek
tűnik, hogy ezeket lássuk el a megfelelő súlyokkal.
A fázishatár mentén átsúlyozva ki tudjuk elégíteni azt a
fizikai elvárást, hogy a fázisátmenet során a két fázis
együtt tudjon létezni. A két eljárás fizikai tartalmát a
3. ábra illusztrálja.
A fenti módszerrel lehetőség nyílt nemeltűnő kémiai
potenciál esetén is az erős kölcsönhatás vizsgálatára. Az
általunk vizsgálni kívánt fázisátmenet, matematikai értelemben
egy szingularitás, valójában véges térfogaton
soha nem jelenik meg, csak a végtelen térfogati határesetben.
Célunk, az átmenet típusainak feltérképezése, a
fázisdiagram megadása a T-µ síkon, csak a térfogatfüggés
feltérképezésével valósítható meg. A fázisátmenetnek
megfelelő szingularitást végtelen térfogati limeszben az
állapotösszeg zérushelye jelzi (érdemes emlékeztetni arra
a tényre, hogy a például a nyomást logZ segítségével
adjuk meg). Véges térfogaton is megjelennek ilyen zérus-
helyek - Lee-Yang-zérók -, igaz ezek nem fizikai, komplex
hőmérsékletekhez tartoznak. Amennyiben végtelen
térfogati limeszben a rendszer valódi fázisátmeneteken
megy keresztül, akkor a Lee-Yang-zérók a térfogat növelésekor
ráhúzódnak a valós tengelyre. Amennyiben csak
egy gyors, de analitikus átmenettel állunk szemben,
akkor a Lee-Yang-zéróknak a végtelen térfogati limeszben
is lesz nem eltűnő képzetes részük, az átmenet analitikus
marad. A Lee-Yang-zérók képzetes részének vizsgálata
így lehetővé teszi a szingularitásra vezető fázisátmenet
és az analitikus átmenet megkülönböztetését.
A 4. ábra mutatja a végeredményt. Két fázist különböztetünk
meg. Az alacsony hőmérsékletű fázist hadronikus
fázisnak nevezzük (ebben a fázisban a tipikus szabadsági
fokok a hadronok, kvarkokból és antikvarkokból
álló kötött részecskék). A magas hőmérsékletű fázist
kvark-gluon plazma fázisnak nevezzük (ebben a fázisban
a tipikus szabadsági fokok a kvarkok és gluonok). A
két állapot közötti átmenetet µ = 0 esetén az irodalom
részletesen tanulmányozta. Egészen a közelmúltig teljesen
ismeretlen volt viszont az átmenet függése az anyagsűrűségtől,
illetve az anyagsűrűség hangolására alkalmas
kémiai potenciáltól. Ahogy a 4. ábrán láthatjuk, zérus és
kis kémiai potenciál esetén a két fázis közötti átmenet
egy gyors cross-over. Egy adott hőmérséklet (kb. 162
MeV) és kémiai potenciál (kb. 360 MeV) esetén a fázisátmenet
másodrendű. A fázisdiagram ezen pontját hívjuk
kritikus végpontnak. Ebben a pontban a kritikus opaleszcenciához
hasonló jelenségek kísérleti megjelenését várjuk.
Ennél is nagyobb kémiai potenciál, illetve kisebb
hőmérséklet esetén a fázisátmenet elsőrendűvé válik.
A fázisdiagram kritikus pontjának tanulmányozása a
németországi GSI (Darmstadt) kutatóintézetben épülő új
részecskegyorsító egyik elsődleges célja.
Összefoglalva azt mondhatjuk, hogy az erős kölcsönhatás
segítségével adhatunk arra a kérdésre választ, hogy mi
történik bármilyen anyaggal, ha egyre jobban felmelegítjük,
illetve egyre jobban összenyomjuk. Egy új rácstérelméleti
módszer segítségével sikerült a fázisdiagram meghatározása,
melynek kísérleti ellenőrzése a közeljövő feladata.
paramétereknél)
fontos konfigurációi jelennek-e meg.
Az irodalomban korábban használt úgynevezett Glasgow-
módszer mélyen a hadronikus fázisban gyűjtött
térkonfigurációkat. Ezeket a fenti módon súlyokkal látta
el, és így számította ki az állapotösszeget. Nyilvánvaló,
hogy a T tengelyen gyűjtött térkonfigurációk fizikai tartalma
teljesen más, mint a a fázishatár túloldalán lévő
fázist jellemző konfigurációké, ezért nem is várható,
hogy bármilyen információt szolgáltassanak a másik fázisról.
Ezért volt a Glasgow-módszer sikertelen. A többparaméteres
átsúlyozás magában a T tengelyen megjelenő
fázisátmeneti pontban gyűjt térkonfigurációkat. Mivel
ezen konfigurációk sokasága vegyesen tartalmazza a
két fázisra jellemző konfigurációkat, ezért kézenfekvőnek
tűnik, hogy ezeket lássuk el a megfelelő súlyokkal.
A fázishatár mentén átsúlyozva ki tudjuk elégíteni azt a
fizikai elvárást, hogy a fázisátmenet során a két fázis
együtt tudjon létezni. A két eljárás fizikai tartalmát a
3. ábra illusztrálja.
A fenti módszerrel lehetőség nyílt nemeltűnő kémiai
potenciál esetén is az erős kölcsönhatás vizsgálatára. Az
általunk vizsgálni kívánt fázisátmenet, matematikai értelemben
egy szingularitás, valójában véges térfogaton
soha nem jelenik meg, csak a végtelen térfogati határesetben.
Célunk, az átmenet típusainak feltérképezése, a
fázisdiagram megadása a T-µ síkon, csak a térfogatfüggés
feltérképezésével valósítható meg. A fázisátmenetnek
megfelelő szingularitást végtelen térfogati limeszben az
állapotösszeg zérushelye jelzi (érdemes emlékeztetni arra
a tényre, hogy a például a nyomást logZ segítségével
adjuk meg). Véges térfogaton is megjelennek ilyen zérus-
helyek - Lee-Yang-zérók -, igaz ezek nem fizikai, komplex
hőmérsékletekhez tartoznak. Amennyiben végtelen
térfogati limeszben a rendszer valódi fázisátmeneteken
megy keresztül, akkor a Lee-Yang-zérók a térfogat növelésekor
ráhúzódnak a valós tengelyre. Amennyiben csak
egy gyors, de analitikus átmenettel állunk szemben,
akkor a Lee-Yang-zéróknak a végtelen térfogati limeszben
is lesz nem eltűnő képzetes részük, az átmenet analitikus
marad. A Lee-Yang-zérók képzetes részének vizsgálata
így lehetővé teszi a szingularitásra vezető fázisátmenet
és az analitikus átmenet megkülönböztetését.
A 4. ábra mutatja a végeredményt. Két fázist különböztetünk
meg. Az alacsony hőmérsékletű fázist hadronikus
fázisnak nevezzük (ebben a fázisban a tipikus szabadsági
fokok a hadronok, kvarkokból és antikvarkokból
álló kötött részecskék). A magas hőmérsékletű fázist
kvark-gluon plazma fázisnak nevezzük (ebben a fázisban
a tipikus szabadsági fokok a kvarkok és gluonok). A
két állapot közötti átmenetet µ = 0 esetén az irodalom
részletesen tanulmányozta. Egészen a közelmúltig teljesen
ismeretlen volt viszont az átmenet függése az anyagsűrűségtől,
illetve az anyagsűrűség hangolására alkalmas
kémiai potenciáltól. Ahogy a 4. ábrán láthatjuk, zérus és
kis kémiai potenciál esetén a két fázis közötti átmenet
egy gyors cross-over. Egy adott hőmérséklet (kb. 162
MeV) és kémiai potenciál (kb. 360 MeV) esetén a fázisátmenet
másodrendű. A fázisdiagram ezen pontját hívjuk
kritikus végpontnak. Ebben a pontban a kritikus opaleszcenciához
hasonló jelenségek kísérleti megjelenését várjuk.
Ennél is nagyobb kémiai potenciál, illetve kisebb
hőmérséklet esetén a fázisátmenet elsőrendűvé válik.
A fázisdiagram kritikus pontjának tanulmányozása a
németországi GSI (Darmstadt) kutatóintézetben épülő új
részecskegyorsító egyik elsődleges célja.
Összefoglalva azt mondhatjuk, hogy az erős kölcsönhatás
segítségével adhatunk arra a kérdésre választ, hogy mi
történik bármilyen anyaggal, ha egyre jobban felmelegítjük,
illetve egyre jobban összenyomjuk. Egy új rácstérelméleti
módszer segítségével sikerült a fázisdiagram meghatározása,
melynek kísérleti ellenőrzése a közeljövő feladata.