
Fizikai Szemle honlap |
Tartalomjegyzék |
Tél Tamás
ELTE TTK, Elméleti Fizikai Tanszék
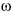 szögsebességgel forgó koordinátarendszerekben
ható fiktív (tehetetlenségi) erő [1],
melynek fellépése abból adódik, hogy a forgó rendszerben
v sebességgel mozgó m tömegű test extra gyorsulásnak
van kitéve, mintha rá még egy erő hatna, a forgástengelyre
merőleges síkban történő mozgás esetén
szögsebességgel forgó koordinátarendszerekben
ható fiktív (tehetetlenségi) erő [1],
melynek fellépése abból adódik, hogy a forgó rendszerben
v sebességgel mozgó m tömegű test extra gyorsulásnak
van kitéve, mintha rá még egy erő hatna, a forgástengelyre
merőleges síkban történő mozgás esetén

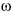 szögsebességgel pozitív
irányban forgó körhintából figyelünk. Itt azt látjuk, hogy
állandó v sebességgel körpályán mozog. Ha rá csak az
szögsebességgel pozitív
irányban forgó körhintából figyelünk. Itt azt látjuk, hogy
állandó v sebességgel körpályán mozog. Ha rá csak az
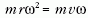 centrifugális erő hatna a forgó rendszerben,
akkor egyre távolabb kellene kerülnie. Ahhoz, hogy körpályán
maradhasson, hatnia kell tehát rá még egy tehetetlenségi
erőnek. Ennek akkorának kell lennie, hogy az eredő
a befelé mutató
centrifugális erő hatna a forgó rendszerben,
akkor egyre távolabb kellene kerülnie. Ahhoz, hogy körpályán
maradhasson, hatnia kell tehát rá még egy tehetetlenségi
erőnek. Ennek akkorának kell lennie, hogy az eredő
a befelé mutató 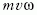 centripetális erőt adja. A hiányzó
erő nagysága így éppen 2
centripetális erőt adja. A hiányzó
erő nagysága így éppen 2 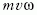 , s ez a Coriolis-erő. Ez a
fiktív erő nevét első részletes leírójáról Gaspard Gustav de
Coriolis-ról (1792-1843) kapta (akinek fő cikke 1835-ban
született). A forgó Földön lezajló jelenségekre gyakorolt
hatására Foucault kísérlete (1851) hívta fel a figyelmet, aki
levezette, hogy a Coriolis-erő következtében az inga lengési
síkjának lassan el kell fordulnia. Kísérletével megmutatta,
hogy a mért és a számolt érték megegyezik, s ezzel
elsôként szolgált bizonyítékkal a Föld forgására [1].
, s ez a Coriolis-erő. Ez a
fiktív erő nevét első részletes leírójáról Gaspard Gustav de
Coriolis-ról (1792-1843) kapta (akinek fő cikke 1835-ban
született). A forgó Földön lezajló jelenségekre gyakorolt
hatására Foucault kísérlete (1851) hívta fel a figyelmet, aki
levezette, hogy a Coriolis-erő következtében az inga lengési
síkjának lassan el kell fordulnia. Kísérletével megmutatta,
hogy a mért és a számolt érték megegyezik, s ezzel
elsôként szolgált bizonyítékkal a Föld forgására [1].
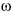 szögsebességű forgás következtében az
egyenletes U sebességgel mozgó test, L út megtétele után
(2. ábra). Kis eltérülést feltételezve, az eltelt idô t = L / U.
Gyorsulása az eredeti irányra merôlegesen
szögsebességű forgás következtében az
egyenletes U sebességgel mozgó test, L út megtétele után
(2. ábra). Kis eltérülést feltételezve, az eltelt idô t = L / U.
Gyorsulása az eredeti irányra merôlegesen 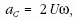 ,
ezért az eltérülés
,
ezért az eltérülés
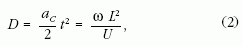

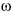 L /U hányados adja. Annak ellenére,
hogy a Coriolis-gyorsulás a sebességgel nő, az eltérülés
fordítottan arányos a sebességgel, ugyanis gyorsabb mozgás
esetén a Coriolis-erô rövidebb ideig hat!
L /U hányados adja. Annak ellenére,
hogy a Coriolis-gyorsulás a sebességgel nő, az eltérülés
fordítottan arányos a sebességgel, ugyanis gyorsabb mozgás
esetén a Coriolis-erô rövidebb ideig hat!
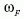 forgási szögsebessége 1 fordulat
(2
forgási szögsebessége 1 fordulat
(2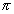 radián)
per nap, azaz 86 400 másodperc, s ezzel
radián)
per nap, azaz 86 400 másodperc, s ezzel 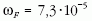 1/s. A vízszintes síkban történő mozgások szempontjából
a Föld forgási szögsebessége vektorának a helyi függőleges
irányba mutató komponense határozza meg a Coriolis-
erőt. Ez a
1/s. A vízszintes síkban történő mozgások szempontjából
a Föld forgási szögsebessége vektorának a helyi függőleges
irányba mutató komponense határozza meg a Coriolis-
erőt. Ez a 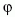 szélességi körön
(
szélességi körön
(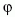 = 0 jelenti az Egyenlítőt,
= 0 jelenti az Egyenlítőt,
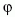 =
= 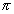 /2 az Északi Sarkot)
/2 az Északi Sarkot) 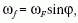 , s így a Coriolis-erő
vízszintes összetevőjének nagysága
, s így a Coriolis-erő
vízszintes összetevőjének nagysága 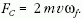 . A
közepes szélességeken, mint hazánkban is számolhatunk
. A
közepes szélességeken, mint hazánkban is számolhatunk
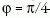 -gyel, azaz
-gyel, azaz 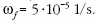 .
Inerciarendszerben semmilyen eltérülést nem tapasztalnánk. Egy
földi laboratórium akkor tekinthető jó közelítéssel inerciarendszernek, ha
benne az eltérülés kicsi. A
.
Inerciarendszerben semmilyen eltérülést nem tapasztalnánk. Egy
földi laboratórium akkor tekinthető jó közelítéssel inerciarendszernek, ha
benne az eltérülés kicsi. A

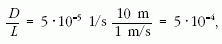
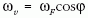 vetülete a lényeges.
Az FC =
vetülete a lényeges.
Az FC = 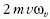 felfelé mutató Coriolis-erő a keletre haladó testeket
emeli, súlyukat csökkenti [3]. Ez az úgynevezett Eötvös-
hatás [1]. Ez a hatás például a kalapácsvetés 80 m-es
hosszát mintegy 5 cm-rel befolyásolja [4]. Az Eötvös-hatás
erősségét a
felfelé mutató Coriolis-erő a keletre haladó testeket
emeli, súlyukat csökkenti [3]. Ez az úgynevezett Eötvös-
hatás [1]. Ez a hatás például a kalapácsvetés 80 m-es
hosszát mintegy 5 cm-rel befolyásolja [4]. Az Eötvös-hatás
erősségét a 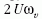 Coriolis-gyorsulás és a g gravitációs
gyorsulás
Coriolis-gyorsulás és a g gravitációs
gyorsulás 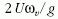 hányadosa határozza meg. Laboratóriumi
értéke a fenti adatokkal 10-3. A szoba tehát valóban
igen jó közelítéssel inerciarendszer.
hányadosa határozza meg. Laboratóriumi
értéke a fenti adatokkal 10-3. A szoba tehát valóban
igen jó közelítéssel inerciarendszer.
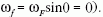 .
.
|
1. táblázat A relatív eltérülés függése a megtett L távolságtól, U = 10 m/s sebesség mellett, közepes szélességeken,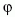 = = 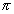 / 4.
(A vizek mozgására jellemzo U = 1 m/s
sebességekkel a D/L értékek rendre 10-szer
nagyobbnak adódnak.) / 4.
(A vizek mozgására jellemzo U = 1 m/s
sebességekkel a D/L értékek rendre 10-szer
nagyobbnak adódnak.)
|
|
| L (km) | D/L (%) |
|
1 10 100 1000 |
0,5 5 50 500 |

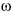 f függőleges szögsebesség-komponens függ a földrajzi
szélességtől. Ennek következtében az adott sebességű
testre ható Coriolis-erő vízszintes összetevője a sarkok
felé közeledve nő.
A mérsékelt égövünkben a ciklonokat és anticiklonokat
az uralkodó nyugati szél lassan kelet felé sodorja.
Pályájuk azonban nem egyenes. Az örvény északi és déli
oldalán az áramlási sebesség közel azonos nagyságú és
ellentétes irányú, az északi oldalon azonban nagyobb az
f függőleges szögsebesség-komponens függ a földrajzi
szélességtől. Ennek következtében az adott sebességű
testre ható Coriolis-erő vízszintes összetevője a sarkok
felé közeledve nő.
A mérsékelt égövünkben a ciklonokat és anticiklonokat
az uralkodó nyugati szél lassan kelet felé sodorja.
Pályájuk azonban nem egyenes. Az örvény északi és déli
oldalán az áramlási sebesség közel azonos nagyságú és
ellentétes irányú, az északi oldalon azonban nagyobb az
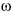 f szögsebesség és ezáltal a Coriolis-erő. A ciklonokban
ezért északra, az anticiklonokban pedig délre mutat az
eredő Coriolis-erő (5.a ábra), s ennek megfelelőn sodródási
irányuk ÉK, illetve DK.
A hurrikánok, tájfunok a meleg trópusi vidékeken
keletkeznek, gyűjtőnevük ezért trópusi ciklon. (A trópusi
nem egyenlítőit jelent, hiszen ott, mint láttuk, a vízszintes
síkban nem hat a Coriolis-erő, ezért egyenlítői ciklonok
nem létezhetnek.) A trópusi ciklonok a 15 fok körüli szélességen
alakulnak ki, ezért őket az ott uralkodó passzátszelek
nyugat felé sodorják. Az eredő Coriolis-erő ugyanolyan
jellegű, mint mérsékeltövi társaikban, de a jóval
gyorsabb szelek (200 km/h) miatt jóval nagyobb. Az tehát,
hogy az Atlanti-óceán déli medencéjében keletkező
hurrikánok nem egyszerűen áthaladnak Közép-Amerikán,
hanem következetesen az USA partjai felé kanyarodnak
el (5.b ábra), a Coriolis-hatás földrajzi szélességtől
való függésének bizonyítéka!
f szögsebesség és ezáltal a Coriolis-erő. A ciklonokban
ezért északra, az anticiklonokban pedig délre mutat az
eredő Coriolis-erő (5.a ábra), s ennek megfelelőn sodródási
irányuk ÉK, illetve DK.
A hurrikánok, tájfunok a meleg trópusi vidékeken
keletkeznek, gyűjtőnevük ezért trópusi ciklon. (A trópusi
nem egyenlítőit jelent, hiszen ott, mint láttuk, a vízszintes
síkban nem hat a Coriolis-erő, ezért egyenlítői ciklonok
nem létezhetnek.) A trópusi ciklonok a 15 fok körüli szélességen
alakulnak ki, ezért őket az ott uralkodó passzátszelek
nyugat felé sodorják. Az eredő Coriolis-erő ugyanolyan
jellegű, mint mérsékeltövi társaikban, de a jóval
gyorsabb szelek (200 km/h) miatt jóval nagyobb. Az tehát,
hogy az Atlanti-óceán déli medencéjében keletkező
hurrikánok nem egyszerűen áthaladnak Közép-Amerikán,
hanem következetesen az USA partjai felé kanyarodnak
el (5.b ábra), a Coriolis-hatás földrajzi szélességtől
való függésének bizonyítéka!
<>
A szerző köszönetét fejezi ki Gyüre Balázsnak, Jánosi Imrének és Szabó Gábornak a forgó rendszerek dinamikájával kapcsolatos értékes eszmecserékért. Irodalom_________________________________
1 A környezeti áramlásokban a forgatottság jellemzésére az Ro = U/(2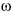 f L ) Rossby-számot használják, mely akkor kicsi, ha a forgás
lényeges. Vegyük észre, hogy a (4) relatív eltérülés a Rossby-számmal
fordítottan arányos D/L = 1/(2Ro). A laboratóriumi mozgások Rossby-száma
tehát nagy. A nagyskálájú környezeti áramlásokban a Rossby-szám
tipikus értéke viszont 10-1-10-2 körüli, a táblázattal összhangban.
Az a tény, hogy a Rossby-szám független a sűrűségtől, jelzi, hogy a
Coriolis-hatás vízben és levegőben egyaránt fontos.
A függőleges mozgás szempontjából a Rossby-szám megfelelője a
g/(2U
f L ) Rossby-számot használják, mely akkor kicsi, ha a forgás
lényeges. Vegyük észre, hogy a (4) relatív eltérülés a Rossby-számmal
fordítottan arányos D/L = 1/(2Ro). A laboratóriumi mozgások Rossby-száma
tehát nagy. A nagyskálájú környezeti áramlásokban a Rossby-szám
tipikus értéke viszont 10-1-10-2 körüli, a táblázattal összhangban.
Az a tény, hogy a Rossby-szám független a sűrűségtől, jelzi, hogy a
Coriolis-hatás vízben és levegőben egyaránt fontos.
A függőleges mozgás szempontjából a Rossby-szám megfelelője a
g/(2U 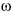 v) hányados.
Ez azonban nem függ a lineáris mérettől, ezért a
Coriolis-erő függőleges komponense (100 km/h-s sebességekig) mindig
elhanyagolható a súly mellett
v) hányados.
Ez azonban nem függ a lineáris mérettől, ezért a
Coriolis-erő függőleges komponense (100 km/h-s sebességekig) mindig
elhanyagolható a súly mellett