Fizikai Szemle honlap |
Tartalomjegyzék |
Kissné Császár Erzsébet, Kiss Miklós Berze Nagy János Gimnázium, Gyöngyös
 Huszonhetedik alkalommal került megrendezésre a
Mikola Sándor Országos Tehetségkutató Fizikaverseny.
A verseny tizedik évfolyamú döntője május 2-4-ig
Sopronban, a kilencedik évfolyamú
döntő május 4-6-ig Gyöngyösön
volt. A versenyt a Vermes Miklós Országos
Fizikus Tehetségápoló Alapítvány
hirdette meg, az Oktatási
Minisztérium, a gyöngyösi Berze
Nagy János Gimnázium, a GYÖNGYÖK
Mátra Művelődési Központ
és Gyöngyös város támogatásával. A
döntőt a Berze Nagy János Gimnázium
és a GYÖNGYÖK Mátra Művelődési
Központ szervezte.
Sajnos
már eggyel több verseny
volt a gyöngyösi, kilencedik évfolyamú
döntő megálmodója, Kiss Lajos
tanár úr nélkül, mint vele.
Az első fordulóban induló mintegy
3000 tanuló közel tizede írhatta
meg a második fordulós dolgozatot,
és ennek alapján ötvenen jutottak a gyöngyösi döntőbe.
A döntősök 16 település 22 iskolájából érkeztek.
A korábban megszokott menetrendtől eltérően a
döntő résztvevői vasárnapdélben érkeztek Gyöngyösre.
A verseny kezdetét egy rézfúvós trió jelezte, amelynek
tagjai két diákunk, Pintér Ábel és Nagy Ádám, valamint
a gyöngyösi Pátzay János Zeneiskola igazgatója,
Jakkel Mihály Zsolt voltak.
A versenyt Czinder Péter, iskolánk igazgatója nyitotta
meg. A zsűri elnöke Simon Péter, a pécsi Leőwey Klára
Gimnázium tanára, tagjai Holics László, az ELTE Apáczai
Csere János Gyakorló Gimnázium, Suhajda János,
a kiskőrösi Petőfi Sándor Gimnázium és Farkas Béláné,
a gyöngyösi Berze Nagy János Gimnázium
tanára.
A megnyitót a 200 perces írásbeli
forduló követte. Közben a kísérő tanárok
Magyarország második leggazdagabb
katolikus egyházi gyűjteményét
nézték meg a Szent Bertalan-
templom Kincstárában Juhász
Ferenc esperes úr segítségével, Benyovszky
Péter kalauzolásával. Utána
Gyöngyös történelmével ismerkedhettek
Gruber Csilla tanárnő vezetésével,
most már együtt a versenyzők
és az őket elkísérő tanárok.
A hétfő a mérés és a megoldások
ismertetésének napja volt.
A verseny izgalmait az esti táncház
segített feloldani, amelyet iskolánk
tanárai, Ombódiné Madai Judit
és Ombódi András vezettek. A versenyzők itt is bizonyították
lelkesedésüket és rátermettségüket.
A keddi eredményhirdetés előtt Várkonyi Péter
kutató, a gömböc egyik feltalálója, a Budapesti Műszaki
és Gazdaságtudományi Egyetem Szilárdságtani
és Tartószerkezeti Tanszékéről - aki 1994-ben első
lett a soproni Mikola-döntőben - tartott előadást A
gömböc története címmel.
A zsűri úgy ítélte meg, hogy a diákok jó munkát
végeztek. Volt egy hibátlan elméleti munka, és néhány
szinte hibátlan mérés.
A Gimnázium kategória legjobb versenyzői:
Simon Péter, a zsűri elnöke átadja az oklevelet Varga Ádámnak, aki
a Szilárd Leó Verseny után a Mikola-versenyt is megnyerte
Várkonyi Péter előadás közben Gömböc-próba az előadás után
Huszonhetedik alkalommal került megrendezésre a
Mikola Sándor Országos Tehetségkutató Fizikaverseny.
A verseny tizedik évfolyamú döntője május 2-4-ig
Sopronban, a kilencedik évfolyamú
döntő május 4-6-ig Gyöngyösön
volt. A versenyt a Vermes Miklós Országos
Fizikus Tehetségápoló Alapítvány
hirdette meg, az Oktatási
Minisztérium, a gyöngyösi Berze
Nagy János Gimnázium, a GYÖNGYÖK
Mátra Művelődési Központ
és Gyöngyös város támogatásával. A
döntőt a Berze Nagy János Gimnázium
és a GYÖNGYÖK Mátra Művelődési
Központ szervezte.
Sajnos
már eggyel több verseny
volt a gyöngyösi, kilencedik évfolyamú
döntő megálmodója, Kiss Lajos
tanár úr nélkül, mint vele.
Az első fordulóban induló mintegy
3000 tanuló közel tizede írhatta
meg a második fordulós dolgozatot,
és ennek alapján ötvenen jutottak a gyöngyösi döntőbe.
A döntősök 16 település 22 iskolájából érkeztek.
A korábban megszokott menetrendtől eltérően a
döntő résztvevői vasárnapdélben érkeztek Gyöngyösre.
A verseny kezdetét egy rézfúvós trió jelezte, amelynek
tagjai két diákunk, Pintér Ábel és Nagy Ádám, valamint
a gyöngyösi Pátzay János Zeneiskola igazgatója,
Jakkel Mihály Zsolt voltak.
A versenyt Czinder Péter, iskolánk igazgatója nyitotta
meg. A zsűri elnöke Simon Péter, a pécsi Leőwey Klára
Gimnázium tanára, tagjai Holics László, az ELTE Apáczai
Csere János Gyakorló Gimnázium, Suhajda János,
a kiskőrösi Petőfi Sándor Gimnázium és Farkas Béláné,
a gyöngyösi Berze Nagy János Gimnázium
tanára.
A megnyitót a 200 perces írásbeli
forduló követte. Közben a kísérő tanárok
Magyarország második leggazdagabb
katolikus egyházi gyűjteményét
nézték meg a Szent Bertalan-
templom Kincstárában Juhász
Ferenc esperes úr segítségével, Benyovszky
Péter kalauzolásával. Utána
Gyöngyös történelmével ismerkedhettek
Gruber Csilla tanárnő vezetésével,
most már együtt a versenyzők
és az őket elkísérő tanárok.
A hétfő a mérés és a megoldások
ismertetésének napja volt.
A verseny izgalmait az esti táncház
segített feloldani, amelyet iskolánk
tanárai, Ombódiné Madai Judit
és Ombódi András vezettek. A versenyzők itt is bizonyították
lelkesedésüket és rátermettségüket.
A keddi eredményhirdetés előtt Várkonyi Péter
kutató, a gömböc egyik feltalálója, a Budapesti Műszaki
és Gazdaságtudományi Egyetem Szilárdságtani
és Tartószerkezeti Tanszékéről - aki 1994-ben első
lett a soproni Mikola-döntőben - tartott előadást A
gömböc története címmel.
A zsűri úgy ítélte meg, hogy a diákok jó munkát
végeztek. Volt egy hibátlan elméleti munka, és néhány
szinte hibátlan mérés.
A Gimnázium kategória legjobb versenyzői:
Simon Péter, a zsűri elnöke átadja az oklevelet Varga Ádámnak, aki
a Szilárd Leó Verseny után a Mikola-versenyt is megnyerte
Várkonyi Péter előadás közben Gömböc-próba az előadás után
(Dudics Pál)
2. Egy kis méretű gumilabdát 30°-os hajlásszögű sima, rögzített lejtő felett, kezdősebesség nélkül elengedve az a lejtő aljától 80 cm távolságban, vízszintes irányban pattan vissza a felületről.(Szkladányi András)
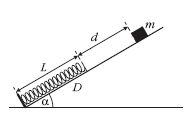 3. α = 30°-os hajlásszögű
lejtő alján L = 1,8 m hosszú,
D = 12 N/m direkciós
erejű csavarrugó van kitámasztva
az ábra szerint. A
rugó felső végétől d = 1
m-re elhelyezett, kisméretű, m = 1,6 kg tömegű test kezdősebesség
nélkül lecsúszik, és a rugónak ütközik. Mekkora
lesz mozgása során a test legnagyobb sebessége, ha
3. α = 30°-os hajlásszögű
lejtő alján L = 1,8 m hosszú,
D = 12 N/m direkciós
erejű csavarrugó van kitámasztva
az ábra szerint. A
rugó felső végétől d = 1
m-re elhelyezett, kisméretű, m = 1,6 kg tömegű test kezdősebesség
nélkül lecsúszik, és a rugónak ütközik. Mekkora
lesz mozgása során a test legnagyobb sebessége, ha
(Holics László)
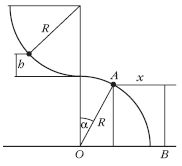 4. Kis méretű test súrlódásmentesen
mozog, az
ábrán látható módon,
két csatlakozó körívből
kialakított jeges pályán.
4. Kis méretű test súrlódásmentesen
mozog, az
ábrán látható módon,
két csatlakozó körívből
kialakított jeges pályán.
Kiss Miklós
) Gimnázium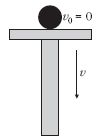 1. Egy nagy tömegű dugattyú lefelé
mozog állandó, 2 m/s sebességgel,
amelyet elhanyagolható idő alatt, hirtelen
vett fel. A dugattyún kezdetben
egy kis tömegű golyó nyugodott,
amely a dugattyú indulása után szabadon
kezdett esni. Amikor utolérte a
dugattyút, azzal rugalmasan ütközött.
1. Egy nagy tömegű dugattyú lefelé
mozog állandó, 2 m/s sebességgel,
amelyet elhanyagolható idő alatt, hirtelen
vett fel. A dugattyún kezdetben
egy kis tömegű golyó nyugodott,
amely a dugattyú indulása után szabadon
kezdett esni. Amikor utolérte a
dugattyút, azzal rugalmasan ütközött.
(Kiss Miklós)
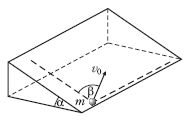 2. m = 2 g tömegű kicsiny
testet v = 5 m/s kezdősebességgel
felfelé lökünk
egy α = 30°-os hajlásszögű
lejtő síkjában. A sebességvektor
a lejtő oldalával
β = 60°-os szöget zár be.
2. m = 2 g tömegű kicsiny
testet v = 5 m/s kezdősebességgel
felfelé lökünk
egy α = 30°-os hajlásszögű
lejtő síkjában. A sebességvektor
a lejtő oldalával
β = 60°-os szöget zár be.
(Horváth Gábor)
(Holics László)
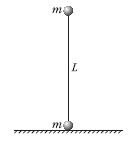 4. Vízszintes, súrlódásmentes felületen
egy L = 35 cm hosszú, elhanyagolható
tömegű rudat tartunk
labilis egyensúlyi helyzetben. A
rúd végeihez kis méretű, m = 0,2
kg tömegű golyókat erősítettünk.
Egy adott pillanatban a rudat elengedjük.
4. Vízszintes, súrlódásmentes felületen
egy L = 35 cm hosszú, elhanyagolható
tömegű rudat tartunk
labilis egyensúlyi helyzetben. A
rúd végeihez kis méretű, m = 0,2
kg tömegű golyókat erősítettünk.
Egy adott pillanatban a rudat elengedjük.
(Kotek László)
 A léc 45°-os szögben rögzítve
van a kémcsőfogó és a
szorítódió segítségével. Helyezd
el az érmét a lécen, és
engedd lecsúszni! Mérd meg
az ábrán bejelölt értékeket,
és ezek segítségével határozd
meg a fa és az érme közötti
csúszási súrlódási együtthatót.
(A berendezést nem célszerű
szétszedni, elállítani, az
adott elrendezésből hozd ki a
legtöbbet!)
A mérésben segítségedre
van az indigópapír, amelyre
az érme, ha ráesik, megjelöli
az alatta lévő papíron a
becsapódás helyét. A papírt
a rajztáblához tudod rögzíteni.
Feladatok
A léc 45°-os szögben rögzítve
van a kémcsőfogó és a
szorítódió segítségével. Helyezd
el az érmét a lécen, és
engedd lecsúszni! Mérd meg
az ábrán bejelölt értékeket,
és ezek segítségével határozd
meg a fa és az érme közötti
csúszási súrlódási együtthatót.
(A berendezést nem célszerű
szétszedni, elállítani, az
adott elrendezésből hozd ki a
legtöbbet!)
A mérésben segítségedre
van az indigópapír, amelyre
az érme, ha ráesik, megjelöli
az alatta lévő papíron a
becsapódás helyét. A papírt
a rajztáblához tudod rögzíteni.
Feladatok
(Kiss Miklós)