Fizikai Szemle 2008/5. 167.o.
LANDAU, AZ ISKOLATEREMTŐ
Sólyom Jenő
MTA Szilárdtestfizikai és Optikai Kutatóintézet
A száz éve született Lev Davidovics Landau a leningrádi
egyetem fizikus hallgatója volt, amikor 1926-ban
első cikke [1] megjelent a Zeitschrift für Physikben A
kétatomos molekulák spektrumának elméletéhez címmel.
Ebben az "új kvantummechanikának” megfelelően
határozta meg - perturbációszámítást alkalmazva -
a molekula gerjesztési spektrumát, az átmenetek intenzitását,
elektromos és mágneses tér jelenlétében is.
Igaz, hogy 18 éves kora ellenére már egyetemi tanulmányai
vége felé járt, de alig vagyunk egy évvel Heisenbergnek
a modern kvantummechanikát megalapozó
cikke után. Egy évvel később megjelent munkájában
[2] pedig eredeti módon, az azóta sűrűségmátrixként
ismert mennyiség bevezetésével vizsgálta a csillapodás
problémáját a hullámmechanikában. Életének
utolsó, Az alapvető kérdésekről című munkája pedig
1960-ban jelent meg a Wolfgang Pauli születésének
hatvanadik évfordulója alkalmából kiadott kötetben.
A közben eltelt három és fél évtizedben a fizika sok
területén alkotott maradandót. Ha egy mostanában
megjelenő szilárdtest-fizikai, magfizikai, térelméleti vagy
más tankönyv tárgymutatóját fellapozzuk, többek között
a következő indexelemekkel találkozhatunk: Landau-csillapodás,
Landau-diamágnesség, Landau-ghost, Landau-
mérték, Landau-pólus, Landau-szintek, Ginzburg-
Landau-egyenletek, Ginzburg-Landau-modell, Ginzburg-
Landau-funkcionál, Landau-Lifsic-egyenletek, Bothe-
Landau-formula, Landau-Placzek-formula, Landau-
Zener-formula, a másodrendű fázisátalakulások Landau-elmélete,
a Fermi-folyadékok Landau-elmélete, a turbulencia
Landau-Hopf-elmélete.

Az 1962 januárjában bekövetkezett tragikus baleset
tehát egy termékeny, a fizika fejlődését rendkívüli
módon előrevivő életet tört ketté. Pedig munkásságát
nemcsak a baleset zavarta meg. Lehet, hogy csak óvatosságának
köszönhette, hogy nem lett a sztálini tisztogatás
áldozata. 1937-ben akkor hagyta ott Harkovot -
szinte egyik napról a másikra és kért menedéket régi
pártfogójától, Pjotr Kapicától -, amikor kollégáját és
barátját, a kísérleti fizikus Lev Subnyikovot, akivel egy
időben volt a harmincas évek elején hosszabb tanulmányúton
Nyugat-Európában, kémkedés vádjával letartóztatták.
Amikor a következő évben ő is börtönbe
került, valószínűleg maga sem tudta, ez csak évtizedek
múlva került nyilvánosságra, hogy Subnyikovot letartóztatása
után néhány hónappal kivégezték.
A Landau munkáinak gyűjteményét [3] kezébe vevő
olvasónak legfeljebb az tűnhetett fel, hogy míg 1934-
ben és 1935-ben is négy cikke jelent meg, emellett
1935-ben két könyve, 1936-ban hat, 1937-ben pedig
tíz cikke, s ekkor készült el az Elméleti fizika sorozat
első tagja, a Statisztikus fizika, addig 1938-ban csak
kettő, 1939-ben pedig mindössze egy cikke. A hivatalos,
a halála idején írt életrajz mégcsak nem is utalhatott
arra, hogy mi lehetett ennek az oka. Ahogy arra is
csak igen áttételesen, hogy miért foglalkozott az 1950-
es évek elején Landau parciális differenciálegyenletek
numerikus megoldásával. Ha az olvasó nem találta
volna ki, a szovjet atom- és hidrogénbomba-programhoz
kellettek ezek a számítások.
A Landau-iskola és az elméleti minimum
A kvantummechanika születése utáni időben tevékenykedő
fizikusok között nem ő volt az egyetlen,
akinek munkássága a fizikán belül több, ma igen különbözőnek
tekintett területre terjedt ki. Elég, ha csak
Hans Bethére vagy Werner Heisenbergre gondolunk.
Valószínűleg a legtöbben nem úgy tekintünk rájuk,
mint a szilárdtestfizika jellegzetes képviselőire, pedig
a Heisenberg-modell említése nélkül nem lehet a
mágnességről tanulni. A Heisenberg-modell egydimenziós
változatának megoldására javasolt Bethe-feltevés
nem ennyire közismert, de minden egyetemi
oktató örülhetne, ha hallgatói annyit tudnának a fémek
elektronelméletéről, amennyit az 1930-as évek
elején a Handbuch der Physik számára készült összefoglalóban
[4] Arnold Sommerfeld és Bethe leírt.
Mégis azt mondhatjuk, hogy Landau munkássága
ezekénél lényegesen szélesebb ölelésű volt. Őt élete
végéig az jellemezte, hogy az elméleti fizikát egységes
tudományterületnek tekintette. Nemcsak pályája elején
foglalkozott egyszerre a fázisátalakulások elméletével,
a fémek nagyon alacsony hőmérsékleti viselkedésével,
a szupravezetéssel, a csillagok energiájának
eredetével, a magok statisztikus elméletével, a neon
és szén alfa-bomlással szembeni stabilitásával, vagy a
nehéz részecskék által keltett záporok kialakulásával
(ezek mind 1937-ben jelentek meg), hanem az 1950-
es évek közepén is több témában volt érdekelt. Ekkor
dolgozta ki a Fermi-folyadékok elméletét, miközben
cikkek sorát írta a kvantumtérelmélet problémáiról.

Talán még ennél is jellegzetesebb vonás az a tudatos
iskolateremtés, amely Landaut a harkovi időktől kezdve
jellemezte. Ha a Landau nevéhez köthető fogalmakat
keressük, a fent felsoroltak mellett, vagy még azok előtt,
a Landau-iskola és "A Landau-Lifsic”, vagyis a Landau és
Jevgenyij Lifsic által írt elméleti fizika tankönyvsorozat
juthat eszünkbe. Landau szerint az elméleti fizikát csak
akkor lehet eredményesen művelni, ha a jelölt széles
alapokkal rendelkezik. Nemcsak maga volt univerzális,
hanem munkatársaitól is ezt várta. Ezért mindenkit, aki
mellette szeretett volna tudományos munkát végezni,
levizsgáztatott az "elméleti minimum”-ból. Mint ismert,
mindössze 43-an állták meg a próbát. Közülük a legismertebbek
Jevgenyij Lifsic mellett még Harkovból Alekszandr
Ahiezer, Iszaak Pomerancsuk és Tisza László, a
moszkvai időből pedig talán Alekszej Abrikoszov (maga
is Nobel-díjas), Lev Gorkov, Igor Dzjalosinszkij, Iszaak
Halatnyikov és Lev Pitajevszkij.
A Landau-Lifsic-sorozatból képet kaphatunk arról,
hogy mit jelentett ez a minimum. A mechanikától az
elektromágneses tér klasszikus elméletén, a szilárd
testek elektrodinamikáján és a kvantummechanikán
keresztül a statisztikus fizikáig terjedt a megkövetelt
ismeretek köre. Életében hét kötet jelent meg a tervezett
sorozatból. Halála után Lev Pitajevszkij segített a
teljessé tételben. A könyveket angolra, franciára, németre,
sőt magyarra is lefordították, valószínűleg más
nyelvekre is, így Landau közvetlen tanítványain túl
fizikusok nemzedékei nőttek fel azokon.
Az iskolateremtés része volt a Landau-szeminárium
is, ahol csoportjának tagjai számoltak be munkájukról,
illetve ismertettek cikkeket. Amíg aktív volt, Landau
az első sorban ült mindig ugrásra készen, ha valamivel
nem értett egyet.
Ebben a cikkben három példán keresztül szeretném
bemutatni a rá és a Landau-iskolára jellemző
gondolkodásmódot.
A Landau-diamágnesség
Az első példa a Landau-diamágnesség és a De Haas-
Van Alphen-jelenség Landau-féle tárgyalása. A klaszszikus
mechanikából tudjuk, hogy ha egy q töltésű
részecske A vektorpotenciállal megadott B mágneses
térben mozog, kinetikus energiáját az mv = p - qA
kinetikus impulzus segítségével lehet
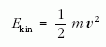
alakban megadni. A kvantummechanikai tárgyalásban
operátorokat használva és a p kanonikus impulzusra
megkövetelve a kanonikus felcserélési relációt a
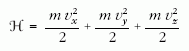
Hamilton-operátor sajátérték-problémáját kell megoldani. Az
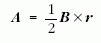
szimmetrikus mértéket használva a q = -e töltésű
elektronokra,
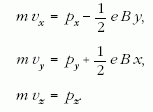
Ezt a problémát, valójában egy ennél bonyolultabbat,
mert a részecske nem szabadon, hanem harmonikus
(parabolikus) potenciáltérben mozgott, Vlagyimir
Fock már 1928-ban megoldotta [5]. Azt a ma már egyáltalán
nem meglepő eredményt kapta, hogy a mágneses
térre merőleges síkban klasszikusan ωc = eB/m
körfrekvenciával mozgó részecske energiája ħωc egységekben
van kvantálva. Az energia-sajátértékek:
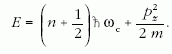
Fock a sajátfüggvényeket is megadta az általánosított
Laguerre-polinomok segítségével. A megoldásból
azonban egyáltalán nem látszott, hogy mekkora az
egyes energiaszintek elfajultsága. Landau 1930-ban
megjelent munkájának [6] első érdekes eredménye e
kérdés megválaszolása volt. Rámutatott arra, hogy ha
a Ψ sajátfüggvényeket
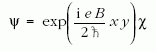
alakban választjuk, χ is a szabad elektronok kinetikus
energiáját tartalmazó fenti Hamilton-operátor sajátfüggvénye
ugyanazzal az energiával, de az azóta Landaumértéknek
nevezett A = (0,Bx,0) mértékben, vagyis
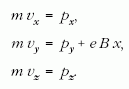
Ebben az alakban a feladat olyan oszcillátorokra
vezethető vissza, amelyek középpontja az x tengely
mentén jól meghatározott, x0 = -py/eB helyeken lehet.
A py impulzus lehetséges kvantált értékeiből kapta
meg az energiaszintek Nρ = eΦ/ħ degenerációját, ahol
Φ a minta felületén áthaladó mágneses fluxus.
Az energiaspektrum ismeretében viszonylag egyszerűen
jutott el a nagykanonikus potenciál
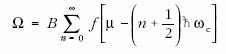
alakjához, ahol
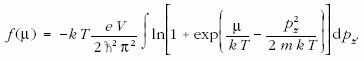
Az n szerinti összegzés elvégzésére a
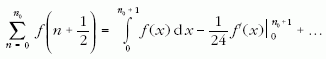
Euler-Maclaurin-féle összegképletet használta, majd a
nagykanonikus potenciálból a mágnesezettséget és a
szuszceptibilitást is meghatározta. Így jutott a T → 0
határesetben az elektronok pályamozgásából adódó
jól ismert
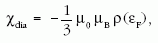
Landau-féle diamágneses szuszceptibilitáshoz, ahol
ρ(εF) az elektronok állapotsűrűsége a Fermi-energiánál.
Az előjelkülönbségtől eltekintve ez pontosan
egyharmada a spinektől származó Pauli-féle paramágneses
szuszceptibilitásnak.
Önmagában ez az eredmény is nagyszerű teljesítmény
lett volna. Landau igazi fizikusi hozzáállása,
érettsége azonban az ehhez az eredményhez fűzött
megjegyzésekben nyilatkozott meg igazán. Először is
rámutatott arra, hogy ha nem szabad elektronokra végezte
volna el a számolást, hanem a kristályrács periodikus
potenciálterében, akkor - mivel a spineket és
a Pauli-féle szuszceptibilitást a periodikus potenciál
nem befolyásolja, a Bloch-elektronok dinamikája viszont
nem azonos a szabad elektronokéval - az egyharmados
arány felborulhat a diamágneses és paramágneses
járulék között, és a bizmuthoz hasonlóan
az eredő viselkedés diamágneses lehet.
Másrészt, felhívta a figyelmet arra, hogy a Bohr-féle
kvantálásnak megfelelő kvantált energiaszintek akkor
alakulhatnak ki, ha az elektronoknak van idejük legalább
néhányszor körbefutni a periodikus pályán. Ha
a minta szennyezett, s emiatt a közepes szabadúthossz
összemérhető a ciklotronpálya sugarával vagy
kisebb annál, a diamágneses szuszceptibilitás lényegesen
megváltozhat. Ugyanezt kell tapasztalni akkor
is, ha a minta mérete válik összemérhetővé a ciklotronsugárral.
Az ebből adódó méreteffektusokat jóval
később, az 1960-as években éppen a Szovjetunióban
vizsgálták igen kiterjedten.
Mindezeknél izgalmasabb Landau harmadik megjegyzése.
Rámutatott arra, hogy az Euler-Maclaurin-féle
összegzési formula csak viszonylag lassan változó
függvényekre alkalmazható. Az adott esetben ez azt
jelenti, hogy teljesülnie kell a µBB << kT feltételnek, ez
viszont sérülhet nagyon alacsony hőmérsékleteken
vagy erős mágneses terekben. Mint írta: "Az utóbbi
esetben a mágneses momentum a mágneses térnek
bonyolult nemlineáris függvénye lehet, sőt a térerősség
függvényében erős periodicitást mutatna.” Ezzel
lényegében megjósolta a De Haas-Van Alphen-jelenséget.
Hozzátartozik azonban az igazsághoz, hogy a
jelenséget az akkori kísérleti lehetőségek mellett megfigyelhetetlennek
vélte. Becslést végzett arra, hogy az
akkor elérhető legerősebb, 30 tesla nagyságú mágneses
térnek mennyire kell homogénnak lennie, hogy a
jelenség ne mosódjon el, s azt találta, hogy a térerősség
0,1%-os inhomogenitása már kiátlagolja az oszcillációkat.
A sors fintora, hogy még ugyanabban az
évben, a már említett, akkor Leidenben dolgozó Subnyikovnak
De Haasszal együtt [7] sikerült megfigyelnie
az energiaszintek kvantáltsága miatt az ellenállásban
megjelenő oszcillációt, majd De Haas és Van
Alphen [8] a mágnesezettség oszcillációit is meg tudta
mérni. Egyébként a De Haas-Van Alphen-jelenség
pontosabb elméleti leírását, az oszcilláló tag helyes
hőmérsékletfüggését is Landau adta meg később,
1939-ben [9], gömbszerű Fermi-felülettel rendelkező
fémekre, az Euler-Maclaurin-összegzés helyett a Poisson-
összegzést alkalmazva.
A másodrendű fázisátalakulások
Landau-elmélete
A második példa a másodrendű (folytonos) fázisátalakulások
Landau-elmélete és annak alkalmazása szupravezetőkre,
ami a Ginzburg-Landau-elmélethez vezetett.
Itt két olyan motívumra figyelhetünk fel, amely
jellemző volt Landaura. Az egyik a szimmetriák szerepének
hangsúlyozása a fizikai elméletekben. Amikor
Landau az 1930-as években a folytonos fázisátalakulásokkal
kezdett foglalkozni, még egyáltalán nem volt
tisztázva, hogy mikor lehet vagy nem lehet folytonos
egy fázisátalakulás abban az értelemben, ahogy folyadékból
folytonosan át lehet menni a gázfázisba. Landau
mutatott rá arra [10], hogy ilyen értelemben nem
lehet folytonos az átalakulás a kristályos állapotból a
folyadékba vagy a kristály egy más szimmetriájú állapotába.
Ezek az átalakulások ugyanis mindig
szimmetriaváltozással, szimmetriaelemek eltűnésével vagy
új szimmetriaelemek megjelenésével járnak együtt,
márpedig "egy szimmetriaelem vagy jelen van, vagy
hiányzik, de semmiféle közbenső állapot nem lehetséges.
Ezért abszolút lehetetlen olyan folytonos fázisátalakulás
(a folyadék és gáz folytonos átalakulásának
értelmében), amely szimmetriaváltozással járna.” Ezt
az állítást Phil Anderson annyira fontosnak érezte,
hogy a szilárdtestfizika első főtételének nevezte [11] a
következő megfogalmazásban: "a szimmetriát nem
lehet folytonosan változtatni”.

A másodrendű fázisátalakulásoknál Landau szerint
sérül a magas hőmérsékleti fázis szimmetriája. A sérült
szimmetriájú fázist egy, a rendre jellemző új mennyiség,
a rendparaméter véges értéke írja le. Mivel az átalakulási
pontban a rendparaméter nulla értéket vesz fel és
onnan folytonosan növekszik, értéke az átalakulási pont
közelében még kicsi. Ezért, ha a szabadenergiát ennek
hatványai szerint sorba fejtjük, elegendő az első néhány
tagot megtartani. Egy kis paraméter keresése volt az a
másik jellegzetes vonás, amire utaltam.
A másodrendű fázisátalakulások Landau-elmélete
[10] ezt a kettőt, a szimmetriamegfontolásokat és a kis
paraméter létezésének következményeit ötvözte. Ha a
δρ rendparamétert a magas szimmetriájú fázis szimmetriacsoportja
irreducibilis ábrázolásainak bázisfüggvényei
szerint kifejtjük, a
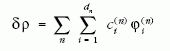
alakra jutunk, ahol n indexeli az irreducibilis ábrázolásokat,
dn pedig annak dimenziója. Ebben a felírásban
a 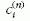 együtthatók tekinthetők kis paraméternek, a
rendezett fázis szabadenergiája ezek hatványai szerint
haladó sorban adható meg:
együtthatók tekinthetők kis paraméternek, a
rendezett fázis szabadenergiája ezek hatványai szerint
haladó sorban adható meg:
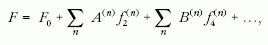
ahol
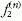 , illetve
, illetve 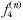 az n-edik irreducibilis ábrázoláshoz
tartozó
az n-edik irreducibilis ábrázoláshoz
tartozó 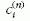 együtthatókból alkotott másodrendű,
illetve negyedrendű kifejezés. Ezeket abból a megkötésből
határozhatjuk meg, hogy a szimmetriasértés ellenére a
szabadenergiának magának, mint a rendszer fizikai
állapotát jellemző mennyiségnek, invariánsnak kell
lennie a rendezetlen fázis minden szimmetriaműveletével
szemben. A szabadenergiát a
együtthatókból alkotott másodrendű,
illetve negyedrendű kifejezés. Ezeket abból a megkötésből
határozhatjuk meg, hogy a szimmetriasértés ellenére a
szabadenergiának magának, mint a rendszer fizikai
állapotát jellemző mennyiségnek, invariánsnak kell
lennie a rendezetlen fázis minden szimmetriaműveletével
szemben. A szabadenergiát a 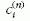 együtthatók szerint
minimalizálva kapjuk a szimmetriasértő fázisban a
rendparaméter értékét. Harmadrendű invariáns azért
nem jelent meg a sorfejtésben, mert elrontaná a folytonos
átalakulást. Ezt a kikötést éppen arra lehet felhasználni,
hogy kiszűrjük, melyik alcsoport lehet a rendezett
fázis szimmetriacsoportja és melyik nem.
A Landau-elmélet jól ismert alakjához akkor jutunk,
ha csak egyetlen irreducibilis ábrázolással van dolgunk,
és a rendparaméter skaláris. Ilyenkor a szabadenergia
szokásos
együtthatók szerint
minimalizálva kapjuk a szimmetriasértő fázisban a
rendparaméter értékét. Harmadrendű invariáns azért
nem jelent meg a sorfejtésben, mert elrontaná a folytonos
átalakulást. Ezt a kikötést éppen arra lehet felhasználni,
hogy kiszűrjük, melyik alcsoport lehet a rendezett
fázis szimmetriacsoportja és melyik nem.
A Landau-elmélet jól ismert alakjához akkor jutunk,
ha csak egyetlen irreducibilis ábrázolással van dolgunk,
és a rendparaméter skaláris. Ilyenkor a szabadenergia
szokásos
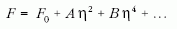
alakjából az A és B együtthatókra tett ismert
feltevésekkel lehet az átalakulás termodinamikáját leírni.
Még ugyanebben az évben, 1937-ben, Landau arra
is rámutatott [12], hogy ha az átalakulási pont közelében
megjelenő térbeli inhomogenitásokat is figyelembe
akarjuk venni, akkor a szabadenergia sűrűségében
meg kell engedni a rendparaméter változására jellemző
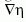 hatványait tartalmazó tagokat is, vagyis az
hatványait tartalmazó tagokat is, vagyis az
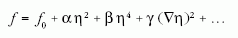
térfogati integrálját kell minimalizálni. Ez volt a
kiindulás a szupravezetés Ginzburg-Landau-elméletének
[13] kidolgozásához. Mikroszkopikus elmélet híján
feltételezték, hogy a rendparaméter a szupravezető
elektronok Ψ hullámfüggvénye, ez a kis paraméter, s a
szabadenergia ennek hatványai szerint fejthető ki. A
többit már a szimmetriamegfontolások diktálták. Ha a
rendparaméter hullámfüggvény jellegű mennyiség, a
szabadenergia nem függhet annak komplex fázisától,
tehát a sorfejtésben |Ψ|2-nek kell megjelennie. Továbbá,
mágneses tér jelenlétében a mértékinvariancia
megköveteli, hogy a hullámfüggvény gradiensét tartalmazó
tagban 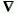 helyett, a korábban említettek szerint,
helyett, a korábban említettek szerint,
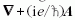 álljon. A mágneses tér energiáját is
figyelembe véve a szupravezető állapot szabadenergiájának
sűrűségére így az
álljon. A mágneses tér energiáját is
figyelembe véve a szupravezető állapot szabadenergiájának
sűrűségére így az
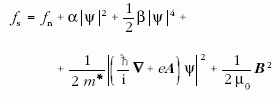
alakot tételezték fel szabad α, β és m* együtthatókkal.
Ennek a szabadenergia-sűrűségnek a hullámfüggvény és a
vektorpotenciál szerinti minimalizálásával jutunk a Ginzburg-
Landau-egyenletekhez.
Nem beszéltünk eddig az e paraméterről. Erre vonatkozóan
Megjegyzik, hogy "nincs semmi ok arra, hogy az elektron
töltésétől különbözőnek vegyük.” Később, amikor a
mikroszkopikus elméletből kiderült, hogy valójában e
helyén 2e -nek kell állnia, Ginzburg
többször említette, szinte szemrehányóan, hogy
ő valójában szerette volna, ha e -t is szabad paraméternek
tekintik, de Landau ragaszkodott a fenti mondathoz.
Bár Landaunak nem volt tökéletesen igaza,
mégis valószínűleg közelebb állt az igazsághoz, mint
Ginzburg. Hiszen ha e szabad paraméter lehetne,
akkor függne a szupravezető anyagi minőségétől, sőt
akár helyfüggő is lehetne. A mértékinvariancia viszont
csak univerzális e-vel teljesíthető. A Cooper-párok 2e
töltése biztosítja az univerzális értéket, de azok létezéséről
akkor még senki sem tudott.
A másodrendű fázisátalakulások Landau-elméletének
a jelentőségét nem csökkenti az, hogy ma már
tudjuk, bizonyos esetekben a kialakuló új állapotot
nem lehet egy lokális rendparaméterrel jellemezni.
Létezhetnek fázisok topologikus renddel vagy rejtett
rendparaméterrel is.
A Fermi-folyadékok Landau-elmélete
A harmadik példa a Fermi-folyadékok Landau-elmélete
[14]. Az már korábban, részben Landau munkásságának
köszönhetően ismert volt, hogy a kondenzált
anyagok viselkedését sokszor bozon jellegű szabad
elemi gerjesztések segítségével lehet értelmezni. A
gerjesztett állapotok spektruma általában rendkívül
bonyolult, de ha csak a fizikai tulajdonságok szempontjából
releváns, a termikus energiával összemérhető
vagy annál kisebb energiájú gerjesztéseket tekintjük,
hiszen csak ezek lehetnek kellő számban
gerjesztve, az ebbe a tartományba eső energiák egy
szabad bozongáz spektrumával azonosíthatók. Ilyen
elemi gerjesztések a rezgő rács viselkedésének tárgyalásánál
megjelenő fononok, a ferro- és antiferromágneses
anyagok mágneses tulajdonságainak megértését
lehetővé tevő magnonok, vagy a szuperfolyékony
héliumban megjelenő rotonok. Mindezek olyan
kollektív gerjesztések, amelyeknek csak a kölcsönható
rendszerben van értelmük. Ha az atomokat összetartó
erőket vagy a mágneses kölcsönhatást képzeletben
kikapcsoljuk, a továbbiakban már nem beszélhetünk
fononokról vagy magnonokról.
A fémek elektromos tulajdonságainak leírásánál
egészen mást tapasztalunk. Az egyszerű fémek viselkedése
nagyon jól modellezhető a szabad, töltés nélküli
fermionokat feltételező Sommerfeld-modellel. A
rács periodikus potenciálja ugyan azt eredményezi,
hogy a Bloch-elektronok dinamikáját nem az elektronok
me tömegével, hanem egy m* effektív tömeggel
kell jellemezni, de az elektronok közötti kölcsönhatás
mintha alig játszana szerepet. Landau lényeges felismerése
az volt, hogy e mögött a szokásos fermionrendszereknek
egy érdekes tulajdonsága rejtőzik. Ha
az elektronok közötti kölcsönhatást adiabatikusan
kapcsoljuk be, a szabad elektronok gázának alapállapota
folytonosan alakul át a kölcsönható rendszer
alapállapotába, az egyrészecskés gerjesztett állapotok
pedig a kölcsönható rendszer gerjesztett állapotaiba
mennek át. Ezért a kölcsönható fermionrendszer gerjesztett
állapotait úgy írhatjuk le, mintha bennük fermion
jellegű kvázirészecskék lennének gerjesztve.
Megint csak Phil Andersonra hivatkozhatunk [11], aki
a kvázirészecske-képhez vezető adiabatikus folytatást
a szilárdtestfizika másik alapelvének tekintette.
Ahhoz, hogy kvantitatív eredményekhez is el lehessen
jutni, szükség volt itt is a kis paraméter megtalálására.
Ezt Landau a kvázirészecskék számában ismerte
fel. Ha 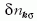 jelöli a ħk
impulzusú, σ spinű kvázirészecskék
számát, akkor a szabadenergia ennek hatványai
szerint kifejthető:
jelöli a ħk
impulzusú, σ spinű kvázirészecskék
számát, akkor a szabadenergia ennek hatványai
szerint kifejthető:
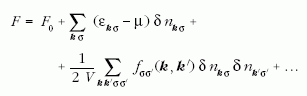
Bár a kvázirészecskék közötti kölcsönhatást egy
többváltozós függvény adja meg, valójában az néhány
paraméterrel helyettesíthető. Így a kölcsönható fermionrendszer
tulajdonságai - nemcsak az ezzel a szabadenergiával
leírható termodinamikai viselkedése,
hanem az ugyanezt a kölcsönhatást tartalmazó transzportegyenletből
származtatható transzporttulajdonságai
is - néhány paraméter segítségével megadhatók.
Az elmélet arra sajnos nem tud választ adni, hogy
egy fermionrendszer mikor tekinthető normálisnak,
mikor lehet benne kvázirészecskéket definiálni, s
mikor sérül az adiabatikus folytonosság. Ma már tudjuk,
hogy vannak nevezetes kivételek. Ilyen a szupravezető
állapot, amely perturbatívan, még ha végtelen
rendig fel is összegezzük a perturbációs sort, nem
állítható elő a szabad elektronok rendszeréből. Ennek
ellenére a kvázirészecske fogalma, Landau többi eredményével
együtt, alapvető szerepet játszik a modern
szilárdtestfizikában.
Irodalom
L.D. Landau, Zeitschrift für Physik 40 (1926) 621.
L.D. Landau, Zeitschrift für Physik 45 (1927) 430.
L.D. Landau Összegyujtött munkái. (oroszul) Nauka, Moszkva,
1969; Collected Papers of L.D. Landau. Pergamon Press, Oxford,
1965.
A. Sommerfeld, H. Bethe: Elektronentheorie der Metalle. in
Handbuch der Physik. Zweite Auflage, Band XXIV. Zwiter Teil,
Verlag von Julius Springer, Berlin, 1933.
V. Fock, Zeitschrift für Physik 47 (1928) 446.
L.D. Landau, Zeitschrift für Physik 64 (1930) 629.
L. Shubnikov, W.J. de Haas, Commun. Phys. Lab. Univ. Leiden, No.
207a, 207d (1930); Proc. Acad. Sci. Amsterdam 33 (1930) 130.
W.J. de Haas, P. M. van Alphen, Commun. Phys. Lab. Univ. Leiden,
No. 208d, 212a (1930); Proc. Acad. Sci. Amsterdam 33
(1930) 1106.
L.D. Landau, Proc. Roy. Soc. A170 (1939) 363.
L.D. Landau, Zh. Eksp. Teor. Fiz. 7 (1937) 19; Phys. Zs. Sowjet.
11 (1937) 26.
P.W. Anderson: Basic Notions of Condensed Matter Physics. The
Benjamin/Cummings Publishing Company Inc., Menlo Park,
California, 1984.
L.D. Landau, Zh. Eksp. Teor. Fiz. 7 (1937) 1232; Phys. Zs. Sowjet.
12 (1937) 123.
V.L. Ginzburg, L.D. Landau, Zh. Eksp. Teor. Fiz. 20 (1950) 1064.
L.D. Landau, Zh. Eksp. Teor. Fiz. 30 (1956) 1058; 32 (1957) 59;
35 (1958) 97.



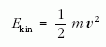
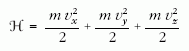
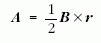
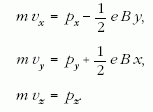
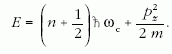
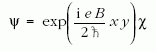
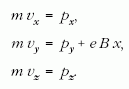
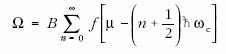
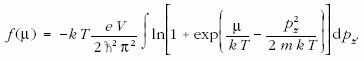
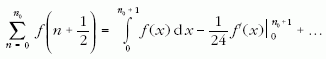
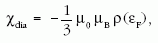

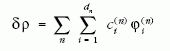
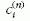 együtthatók tekinthetők kis paraméternek, a
rendezett fázis szabadenergiája ezek hatványai szerint
haladó sorban adható meg:
együtthatók tekinthetők kis paraméternek, a
rendezett fázis szabadenergiája ezek hatványai szerint
haladó sorban adható meg:
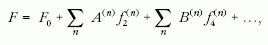
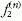 , illetve
, illetve 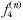 az n-edik irreducibilis ábrázoláshoz
tartozó
az n-edik irreducibilis ábrázoláshoz
tartozó 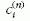 együtthatókból alkotott másodrendű,
illetve negyedrendű kifejezés. Ezeket abból a megkötésből
határozhatjuk meg, hogy a szimmetriasértés ellenére a
szabadenergiának magának, mint a rendszer fizikai
állapotát jellemző mennyiségnek, invariánsnak kell
lennie a rendezetlen fázis minden szimmetriaműveletével
szemben. A szabadenergiát a
együtthatókból alkotott másodrendű,
illetve negyedrendű kifejezés. Ezeket abból a megkötésből
határozhatjuk meg, hogy a szimmetriasértés ellenére a
szabadenergiának magának, mint a rendszer fizikai
állapotát jellemző mennyiségnek, invariánsnak kell
lennie a rendezetlen fázis minden szimmetriaműveletével
szemben. A szabadenergiát a 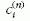 együtthatók szerint
minimalizálva kapjuk a szimmetriasértő fázisban a
rendparaméter értékét. Harmadrendű invariáns azért
nem jelent meg a sorfejtésben, mert elrontaná a folytonos
átalakulást. Ezt a kikötést éppen arra lehet felhasználni,
hogy kiszűrjük, melyik alcsoport lehet a rendezett
fázis szimmetriacsoportja és melyik nem.
A Landau-elmélet jól ismert alakjához akkor jutunk,
ha csak egyetlen irreducibilis ábrázolással van dolgunk,
és a rendparaméter skaláris. Ilyenkor a szabadenergia
szokásos
együtthatók szerint
minimalizálva kapjuk a szimmetriasértő fázisban a
rendparaméter értékét. Harmadrendű invariáns azért
nem jelent meg a sorfejtésben, mert elrontaná a folytonos
átalakulást. Ezt a kikötést éppen arra lehet felhasználni,
hogy kiszűrjük, melyik alcsoport lehet a rendezett
fázis szimmetriacsoportja és melyik nem.
A Landau-elmélet jól ismert alakjához akkor jutunk,
ha csak egyetlen irreducibilis ábrázolással van dolgunk,
és a rendparaméter skaláris. Ilyenkor a szabadenergia
szokásos
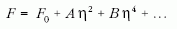
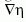 hatványait tartalmazó tagokat is, vagyis az
hatványait tartalmazó tagokat is, vagyis az
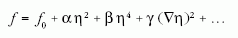
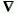 helyett, a korábban említettek szerint,
helyett, a korábban említettek szerint,
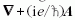 álljon. A mágneses tér energiáját is
figyelembe véve a szupravezető állapot szabadenergiájának
sűrűségére így az
álljon. A mágneses tér energiáját is
figyelembe véve a szupravezető állapot szabadenergiájának
sűrűségére így az
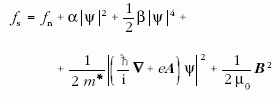
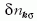 jelöli a ħk
impulzusú, σ spinű kvázirészecskék
számát, akkor a szabadenergia ennek hatványai
szerint kifejthető:
jelöli a ħk
impulzusú, σ spinű kvázirészecskék
számát, akkor a szabadenergia ennek hatványai
szerint kifejthető: