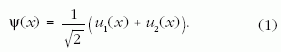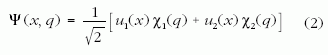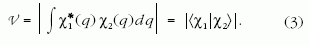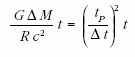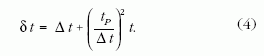Fizikai Szemle 2008/6. 209.o.
KVANTUM ÉS KLASSZIKUS HATÁRÁN
Geszti Tamás
ELTE Fizikai Intézet
Előzmények
Első képeink egyikén Max Planckot látjuk szívbéli
jóbarátjával és örökös kamarazene-partnerével, Albert
Einsteinnel (1. ábra). Ők történetünk korai évtizedeiben
a fizikus közösség élő lelkiismeretének szerepét
játszották: mindig jeleztek, valahányszor a formalizmus
szépsége messzire ragadta a kvantumelmélet
művelőit. Jelzéseik nem mindig voltak közvetlenül
igazak, de mindig jó irányba terelték a fogékony kutatók
gondolkodását.
Planckról általában ilyen időskori, megállapodott
úriembert mutató képeket szokás közölni. 1901-ben
azonban, negyvenhárom évesen, amikor nagy felfedezését
közölte, még inkább sportrepülőnek látszott,
aki kis kétfedelű gépén a rejtélyes kísérleti eredmények
hegycsúcsai fölött átsuhanva, elsőként pillantotta
meg a kvantumfizika termékeny síkságát (2. ábra).
Sokan követték: a fizika benépesítette és belakta a
kvantumjelenségek országát.

A kezdetektől fogva felmerült azonban az igény,
hogy ne feledjük, honnan jöttünk: tegyük járhatóvá az
utat visszafelé, a kvantumfizikából a klasszikus fizikába.
Először úgy látszott, hogy a feladat nem túl nehéz.
Amikor de Broglie és Schrödinger felderítette a
kvantálás mögött rejlő hullámmozgás természetét,
kézenfekvő volt, hogy a klasszikusságot a rövidhullámok
határesetében fedezzék fel. Ezt először Niels
Bohr fogalmazta meg úgy, hogy a nagy kvantumszámok
határesete felel meg a klasszikus fizikába való
átmenetnek; ezt nevezte ő „a korrespondencia elvének”.
Hasonló volt a tartalma annak a matematikailag
részletesen kidolgozott sémának, amelyben Wentzel,
Kramers és Brillouin (WKB) vezette le a rövidhullámok
határesetének matematikáját. Akárhogy is nézzük,
annyi tényleg igaz, hogy rövidhullámokból szuperpozícióval
összerakhatunk olyan hullámcsomagokat,
amelyek a klasszikus mechanika törvényei szerint
mozognak.

Ez azonban nem old meg semmit: a hullámcsomagban
ott van a hullám, amely résekkel vagy nyalábosztókkal
szétválasztva, majd újra egyesítve interferenciára
képes. Addig pedig ez bizony valódi kvantummechanika,
hiszen klasszikus mechanikában a mozgó
testek nem mennek kétfelé, és nem interferálnak!
Azóta számos rendszert ismertünk meg, a félvezető
nanostruktúrákban mozgó elektronoktól az atom- és
molekula-interferométerekig, amelyekben a folyamatok
a rövid hullámok határesetében játszódnak le, de
a kvantummechanikai interferencia zavartalanul működik.
Ezért aztán ezt a határesetet mostanában már
csak „félklasszikusnak” nevezik.
A legjobbak számára hamar világossá válhatott,
hogy a klasszikusság magyarázata a kvantummechanika
oldaláról nézve valójában rettentően nehéz kérdés,
amely legalább két problémakört foglal magába:
a koherencia elvesztését, és a mérésben megnyilvánuló
véletlenszerűség eredetét. Különösen az utóbbi
gonosz, mert ellentmondani látszik a Schrödinger-egyenlet
linearitásának. Bohr volt az, akiben mindez
vészjelzésként fogalmazódott meg: ha a fizikusok
ennek a kibogozásába ölik idejüket-energiájukat, akkor
számtalan fontos és megoldható feladat halasztódik
a beláthatatlan jövőre.

A bohri tanács ez lehetett volna: Tartsátok magatokat
távol a kvantum-klasszikus határ bonyodalmaitól,
érezzétek jól magatokat a kvantumos birodalomban,
használjátok bizalommal a valószínűségek kiszámítására
szolgáló Born-szabályt, és magyarázzatok meg
minél többet a világból!
Hallatlanul bölcs tanács, és sikeres is: a hagyományosan
kvantumos tárgyaknak számító atomok és
molekulák fizikája mellett megszületett és kivirágzott
a kristályos szilárdtestek, atommagok, stabil és pillanatnyi
életű elemi részek sokaságának kvantumelmélete,
amely a lineáris Schrödinger-egyenlet és a kvadratikus
Born-szabály határolta játéktéren belül tetszőlegesen
éles és színekben gazdag képet rajzolt a környező
világról. Ezért igazán szerény árat jelentett az,
hogy évtizedeken át rossz modornak számított a
kvantum-klasszikus átmenet bonyodalmait firtatni.

Sajnos Bohr (3. ábra) zseniális tanácsait egy erősen
tekintélytisztelő tradícióban gyökerező szavakba
öntötte:
- A klasszikus és kvantumos világ egymás mellett
létezik; különböznek egymástól, a kvantumvilágban
van szuperpozíció, a klasszikusban nincs.
- A két világ csak a mérés folyamatában érintkezik
egymással; ilyenkor véletlen választás történik, a
Born-szabály megszabta valószínűségek alapján.
- Mi csak a világ klasszikus felét láthatjuk, a kvantumos
világ csak árnyék.
Ez a keményen koppanó parancssorozat a „koppenhágai
interpretáció” néven vonult be a fizika történetébe.
Akik a fő csapáson dolgoztak, azok számára
mindez csak afféle vitrinbe való dokumentum szerepét
játszotta. Akiket azonban makacsul a kvantum-
klasszikus határvidék nehezen járható, de mégis varázslatos
hegyei érdekeltek, azok számára a frusztráció
forrásává vált. Ezt fejezte ki az elterjedt - Feynmannak
tulajdonított, valójában ismeretlen eredetű -
aranyköpés, amely szerint a koppenhágai interpretáció
tartalma röviden: „Shut up and calculate!” - Magyarul:
Befogod a szád és számolsz!
A lelki áttörést a hatvanas évek végétől John Stuart
Bell hozta meg (4. ábra), aki - miután huszonéves
korában megalkotta főművét, a híres Bell-egyenlőtlenségeket
- óriási lendülettel kezdte támadni
és gúnyolni a koppenhágai szellemű kvantummechanika
világát. Tőle származik a hírhedten
sértő hangulatú betűszó: a kvantummechanika »FAPP«
(For All Practical Purposes, azaz minden gyakorlati
célra) kiválóan működik, miközben az értelme homályban
marad.
Az alábbiakban röviden áttekintjük a huszadik század utolsó
harmadában megszületett elméleti irányzatokat,
amelyek célja a rejtélyes kvantum-klasszikus
határvidék felderítése. A kutatások tartalmilag és technikailag
is világosan két részre oszthatók: a koherencia
elvesztését - a dekoherenciát - lényegében a lineáris
Schrödinger-egyenlet érvényességi körén belül
sikerült megérteni. Ha azonban a mérésben megnyilvánuló
véletlen választást és a hullámfüggvény ezzel
járó, híres „kollapszusát” valóságos fizikai folyamatként
szeretnénk magyarázni, ahhoz óvatosan ki kell
lépni a Schrödinger-egyenlet világából.
Környezet okozta dekoherencia
Hogy a makrovilágban látott testek miért nem képesek
koherens hullámmozgásra, azt először Heinz-
Dieter Zeh értette meg és írta le 1970-es dolgozatában.
Zeh még egy különleges életrevalósági teszten is átment:
egy konferencián több órás diszkusszióban
meggyőzte Wigner Jenőt elképzelése alapvető helyességéről.
Ez sokat lendített azon, hogy a dekoherencia
elméletéből a kvantumelmélet tiszteletreméltó fejezete
fejlődhessen ki.
Az alapgondolat nagyon egyszerű. Induljunk ki egy
anyaghullámból, amelynek amplitúdója két részhullám
amplitúdóinak szuperpozíciója (egyszerűség kedvéért
egyetlen x változó függvényében):
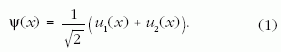
A hullám intenzitását úgy kapjuk meg, hogy ezt az
összeget (abszolút értékben) négyzetre emeljük. Az
interferenciát a négyzetre emeléskor fellépő vegyes
szorzatok összege: u1*(x)u2*(x)u1(x)
hordozza (a csillag komplex konjugálást jelent).
Ha ez az anyaghullám kölcsönhatásba lép a környezettel,
amelynek koordinátáit tömören a q betűvel
jelöljük, az összefonódott hullámfüggvényt közelítőleg
így írhatjuk:
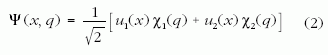
annak megfelelően, hogy a különböző u1 és u2
részhullámok a kölcsönhatás által különböző χ1(q), illetve
χ2(q) állapotok felé terelik a környezetet.
Az intenzitást most is négyzetre emeléssel kapjuk
meg, de az interferenciát változatlanul csak az anyaghullámon
szeretnénk megfigyelni. Ezért a környezet
koordinátáira ki kell integrálni. Az interferenciát kifejező
vegyes szorzatok emiatt - egységnyi nagyságú
fázisszorzóktól eltekintve - megszorzódnak ezzel az
integrállal:
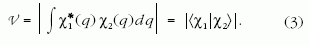
Ha χ1(q) és χ2(q) nagyon eltér egymástól
(a Hilbert-tér
nyelvén szólva: közel ortogonálissá válik), akkor
a fenti integrál (skalárszorzat) sokkal kisebb egynél,
emiatt lecsökken az interferenciajel amplitúdója, az
interferencia láthatósága (angolul „visibility” - ennek
rövidítése a V
betű). Ez a mechanizmusa a koherencia
elvesztésének, a környezeti eredetű dekoherenciának.
Makroszkopikusan különböző állapotok - például
egy macska élő és halott állapota - szuperpozícióit
mérhetetlenül gyorsan dekoherálja a makroszkopikus
testekkel számtalan helyen érintkező környezet. Atomok,
kis molekulák, fotonok sokáig őrizhetik koherenciájukat.
A kettő között található a jól felszerelt
laboratóriumokban létrehozott mezoszkopikus rendszerek
- ioncsapdák, atomcsapdák, mikromézerek,
szupravezető Josephson-áramkörök, félvezető nanoszerkezetek
- rohamosan bővülő világa, amelyek koherenciája
jó esetben egy rövid méréssorozat elvégzéséig
tartható fenn. Az ilyen rendszerekben megfigyelhető
gyenge dekoherencia elmélete jól kidolgozott
apparátussá fejlődött, amely alkalmas konkrét környezeti
hatások kvantitatív vizsgálatára. Az elmélet fő
eszközei a sűrűségmátrix időbeli változását leíró
„kvantumos master-egyenletek”, amelyeket olyan
gyakorlati területeken is rutinszerűen alkalmaznak,
mint a kvantumoptika vagy a mágneses magrezonancia
(valójában az egész módszer ez utóbbi területen
indult először fejlődésnek).
Hogy a környezeti dekoherencia elmélete a klasszikus-
kvantum határ egész jelenségkörét leírhatja, ezt
az álmot a dekoherencia-elmélet másik híressé vált
kutatója, Wojciech Zurek csepegtette a fizikusok tudatába
1981 óta írott cikkei sorozatával. Fogalmak egész
sorát - mutató-állapotok, jósolhatósági szita, kvantum-
darwinizmus stb. - vezette be annak szemléltetésére,
hogy részrendszer és környezet bonyolult dinamikájában
létrejöhet a klasszikusan stabil állapotok
látszólag véletlenszerű kiválasztódása. Az elméletnek
ezt az ágát minden intellektuális szépsége mellett is
sokan hiányosnak érzik, és nem tekintik a feltett kérdésekre
adott meggyőző válasznak.
Kollapszus és vidéke
Mikroszkopikus és makroszkopikus között nincs világos,
értelemszerű határ, ezért természetes dolog lenne
olyan dinamikai törvényt keresni, amelynek kétféle
határesetét jelentenék a Schrödinger-egyenlet és
a Newton-törvények. Az előző pont végén tárgyalt
elképzeléseket az a némiképpen fundamentalista hit
hajtja, hogy ez az áthidaló törvényszerűség maga a
lineáris Schrödinger-egyenlet. Ennek azonban ellene
szólni látszik, hogy véletlenszerűséget általában nemlineáris
jelenségek szoktak létrehozni, aminek az
adott konkrét esetben eléggé ékesszóló alátámasztását
adja a valószínűségeket megadó Born-szabály
kvadratikus volta is. Ezért a kezdetektől fogva kézenfekvő
törekvés volt, hogy próbáljunk meg óvatosan -
a kvantumelmélet nagyszerű eredményeit el nem
rontva - túllépni a törvénnyé vált kereteken. Azt a
törvényt hosszú időre Dirac híres kvantummechanika
könyve véste kőtáblába; amiről ezután lesz szó, az
„nem-Dirac” kvantummechanika.
„Bohm-mechanika”
A Schrödinger-Dirac kvantummechanika nagyszerű
szorításából való kimenekülés legrégebbi stratégiája a
kvantumos mozgás hullámtermészetét elsőnek felismerő
Louis de Broglie-től származik, de részletes kidolgozásában
néhány évtizeddel később David Bohm
játszott döntő szerepet, ezért többnyire „Bohm-mechanika”
néven emlegetik. Ebben a képben pontszerű
részecskék mozognak egy nemlokális „vezérhullám”
vagy „kvantumpotenciál” hatása alatt, szigorú determinizmusban.
A véletlenszerűséget a részecskék kaotikus
mozgása tartja fenn (ezt Bohm idejében még
nem láthatták ilyen világosan, de ma már nyilvánvaló,
hogy enélkül a dolog nem működne); a valószínűségek
kialakításában a részecskék kezdeti valószínűségeloszlásának
van lényeges szerepe. Részecskék és
vezérhullám csatolt dinamikája, némiképpen konspirációszerűen,
a mérési eredményeknek éppen a szokásos
kvantummechanikával megegyező statisztikáját
alakítja ki.
A Bohm-mechanikát a kutatók kicsiny, de lelkes
csapata műveli a világban, tágítgatva a kereteket a
kvantumtérelmélet felé; a fizikusok többsége nem
hiszi, hogy ez az irányzat lényegesen hozzásegítene a
fizika megértéséhez.
Spontán kollapszus
A hagyományosnak mondható kvantummechanika
egyik irritáló - bár nehezen cáfolható - tulajdonsága a
mérési folyamat megkülönböztetett szerepe, amit
John Bell is szenvedélyesen ostorozott: miért éppen a
részecskedetektorok kattanásaihoz kapcsolódik a
lineáris Schrödinger-dinamikával zavartalanul kifejlődő
szuperpozíciók időnkénti összeomlása - kollapszusa
- a szuperpozíció egy véletlenül kiválasztott
tagjára, és miért éppen arra, amit a megfelelő detektor
jelez? Nehezen elfogadható, szubjektív és antropomorf
az a többször kimondott elképzelés, hogy mérési
eredmények tudomásul vétele nélkül a világunk
szétfolyna. Ahogy Einstein mondta egyik fizikus kollégájának
egy esti sétán: „Te tényleg elhiszed, hogy a
Hold nincs ott, ha senki se nézi?”
Egy lehetséges alternatíva az, hogy a kollapszus a
méréstől függetlenül, spontán módon, rendszeresen
megtörténik, valahányszor a kvantumállapot olyan
szuperpozícióvá kezdene szétfolyni, amely valamilyen
mennyiségnek, például egy tárgy helyvektorának
makroszkopikusan különböző értékeit engedi meg.
Annak kiválasztását, hogy milyen érték köré ugorjon
össze a hullámfüggvény, valamilyen véletlen folyamat
szabályozza, ami az elképzelés szerint része a természet
mozgástörvényének.
Ezt matematikailag nem könnyű modellezni. Az
1970-es évek bátortalan próbálkozásai után 1986-ban
közölte a Ghirardi - Rimini - Weber szerzőhármas
azt az egyenletet, amely máig is a véletlen kollapszussal
kibővített Schrödinger-egyenlet prototípusának
számít. További fejlesztésében Pearle, Gisin és Diósi
Lajos nevéhez kapcsolódnak jelentős lépések. Az
elmélet máig is él és fejlődik, annak ellenére, hogy az
eredeti remények - a kísérleti ellenőrzés lehetősége -
eddig nem váltak be: a spontán kollapszust, mint véletlen
zajt kellene megfigyelni, de ez a zaj sokkal
gyengébb, mint a környezettel való kölcsönhatásból
eredő, minden véges hőmérsékleten jelen levő, a dekoherenciáért
is felelős véletlen hatás.
Mindmáig nyitott kérdés az is, hogy esetleg valamilyen
már ismert fizikai hatás okozza-közvetíti a
véletlen kollapszust. Ennek egy ígéretes megközelítését
az alábbiakban külön tárgyaljuk, már csak magyar
vonatkozásai miatt is.
A gravitációs vonal
A kollapszus magyarázatában szóba jöhető ismert
erők közül kiemelt figyelmet kapott a gravitáció. Az,
hogy a G, ħ , c természeti állandókból kikeverhető a
megfelelő dimenziójú Planck-hossz, Planck-tömeg és
Planck-idő, inkább csak a kinematikai keretét jelenti
gravitáció és kvantummechanika összekapcsolódásának.
A gravitáció megszelídítése a kvantumtérelmélet
keretei között hírhedten nehéz, mindeddig megoldatlan
problémaköre az elméleti fizika fő vonalának. Itt
azonban nem erről van szó, bár lehet valami távoli
kapcsolata történetünkkel (lásda fejezet végén).
Azt, hogy a gravitációnak valami köze lehet a kvantum
és klasszikus közötti határ és a kvantummechanikai
mérés problémaköréhez, először Feynman vetette
fel 1962-63-as Lectures on Gravitation című könyvében.
Feynman, akinek - mint a régi görögöknek -
minden és mindennek az ellenkezője is az eszébe
jutott, nem ment utána egyszeri ötletének. Aki először
komolyan vette ezt a lehetőséget, az Károlyházi Frigyes
volt; ő 1966-os dolgozatában kijelölt egy logikai
pályát, amely mentén a gravitáció előidézője lehet a
kvantummechanikai kollapszusnak. Később egy ettől
különböző logikai kapcsolatot vázolt fel Diósi Lajos
(1984, 1987); az ő gondolatmenetét 1996-ban újra
felfedezte Roger Penrose, aki az azóta népszerűvé vált
„Newton-Schrödinger-elmélet” névvel ajándékozta
meg a témakört. Ennek egy változatával a jelen cikk
írója is foglalkozott (2004).
Miért éppen a gravitációnak lenne esélye arra,
hogy megmagyarázza a kvantum-klasszikus átmenet
rejtélyes vonásait? Talán mert kicsi és nagy között az
átmenetet nem túl sok paraméter mentén tudjuk elképzelni.
Ezek egyike a geometriai méret. Ez nem
működik: neutronok, atomok, molekulák méteres
interferométereken át repülnek, centiméterekre szétváló
részhullámokban, néha arasznyi koherenciahosszal,
és a végén vidáman interferálnak. A másik a
tömeg, ami viszont valóban döntő! A C60 és hasonló
méretű molekulák, amelyek tömegközépponti mozgásában
még sikerült interferenciát létrehozni, 10-24 kg
tömegűek (ennél jóval nehezebb molekulák interferenciájában
a szűk keresztmetszet a sugárforrás: ezeket
már nem lehet kályhában elpárologtatni). A létező legkisebb
nanomechanikai oszcillátorok tömege viszont
10-15 kg körüli, mintegy kilenc nagyságrenddel nehezebb;
ezeken eddig nem sikerült kvantumos viselkedést
látni. Ha pedig a tömeg a lényeg, akkor a gravitáció
szerepe kézenfekvően szóba jöhet, mint a jelenségek
mélyebb okozója.
Persze az, hogy a nanomechanikai oszcillátorok
nem mutatnak kvantummechanikai viselkedést, még
nem bizonyítja, hogy ők klasszikus tárgyak! Ennek
igazi ellenőrzéséhez a rezgőmozgás kvantummechanikai
alapállapotának közelébe, az oszcillátor v frekvenciájának
megfelelő hv / kB hőmérsékletre kellene
őket lehűteni (kB a Boltzmann-állandó). Napjainkra
ezt sikerült egy tízes szorzó erejéig megközelíteni, és
őrületes versenyfutás indult, évente tucatnyi Nature
és Physical Review Letters cikkel, a hatékonyabb hűtés,
valamint kvantumállapot-preparálás és -mérés
felé. Közben, megengedve, hogy talán mégis valahol
a kilenc nagyságrendnyi tömegrés közepén lép be
valami új fizikai hatás, intenzív kutatás indult a repíthető
molekuláknál jóval nehezebb szén nanocsövek,
valamint ultrahideg csapdázott gázok esetleges kvantumos
mozgásának feltárására is.
Hogy konkrétan hogyan is hatna a gravitáció a kollapszusra,
arra van egy egyszerű, de nem feltétlen
igaz válasz: a gravitáció vonzó erő, hát persze, hogy
össze tudja rántani a kettéhasadt hullámcsomag részeit!
Közelebbről nézve ez ellenkezik azzal a kvantummechanikai
dogmával, hogy kölcsönhatás csak
két különböző test között lehetséges, önkölcsönhatás
nincs. Lehet azonban, hogy a gravitáció fölötte áll
ennek a szabálynak; ez nemlinearitást vinne be a
kvantummechanikába, de már említettük, hogy talán
éppen az vezetne ki a zsákutcából.
Van egy másik, elvontabb útja is a gravitáció és a
kvantummechanika összekapcsolódásának: ez a gravitációnak
az interferenciára gyakorolt hatása. A gravitáció
gyenge erő, amelynek eltérítő hatását csak
nagy távolságokra repülő tárgyakon vehetjük észre,
de a hullámfüggvény fázisát kis távolságokon is komolyan
tudja módosítani. Hasonló a helyzet a gázok
optikai interferometriájához: a törésmutató gyenge
változásai a fényt csak a délibábhoz hasonló méretekben
tudják eltéríteni, de már a laboratóriumi méretű
Rayleigh-interferométerben is jól mérhető fáziseltolást
okoznak.
Károlyházi a gravitációnak ezt a közvetett, az interferenciára
gyakorolt hatását ismerte fel. A gondolatmenet
összefoglalására válasszuk most azt a kiindulópontot,
hogy egy R nagyságú test Δt = R / c minimális
időbizonytalanságot okoz egy téridőpont kijelölésében.
Ehhez a kvantummechanika szerint
ΔE = ħ / Δt energiabizonytalanság
tartozik, ami a speciális
relativitáselmélet szerint ΔM = ħ / (c2Δt)
tömegbizonytalansággal
jár együtt. Itt lép be az általános relativitáselmélet:
a tömegbizonytalanság az úgynevezett
gravitációs idődilatáció miatt egy t időtartam mérésének
az előzőkben bevezetett Δt bizonytalanságához
hozzáad egy
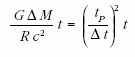
járulékot, ahol
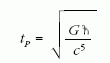
a Planck-idő. A két járulékból összetevődő teljes időbizonytalanság
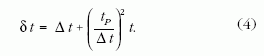
Ennek adott t időtartam mellett a kiinduló Δt egy véges
értékénél lesz az elérhető minimuma, amelyre
teljesül

Ez az érdekes 1/3 kitevőjű hatványfüggés Károlyházinak
amolyan szakmai névjegyeként szerepel a világban.
Az adott megközelítésmód szerint ez a tovább
nem csökkenthető időbizonytalanság mossa el az
időbeli frekvenciák élességét, és vele a kvantummechanikai
koherenciát.
Diósi (és az ugyanazt később újra felfedező Penrose)
kiindulása ettől lényegesen különböző. Ők a
gravitációt, mint vonzó erőt tekintik, amely a kettéhasadt
hullámcsomag („Schrödinger-macska”) két
komponense közötti önkölcsönhatásból eredően egy
ΔU energiát eredményez. Ez határozza meg a kollapszus
ħU időskáláját: minél nagyobb az önkölcsönhatási
energia, annál hamarabb megtörténik a kollapszus.
Diósi változata a teljesebb: ő ezt az időskálát
beteszi a spontán lokalizáció sztochasztikus dinamikai
egyenletébe, és ezáltal konkrét becsléseket ad a
várható zaj szintjére.
A Newton-Schrödinger-önkölcsönhatást vehetjük
nagyon szó szerint is (Diósi 1984): ha a gravitációt a
kvantummechanikán kívül álló klasszikus mezőnek
tekintjük, amelynek forrása a kvantummechanikai
tömegsűrűség várható értéke (ez a nemlétező kvantumgravitációs
elmélet létező átlagtér-közelítése),
akkor ez a külső klasszikus mező, visszahatva a kvantumállapotra,
egy nemlineáris Schrödinger-egyenlettel
leírható dinamikát eredményez.
Erre épül a magam álma ugyanerről a jelenségkörről:
én úgy gondolom, hogy egyáltalán nincs spontán
kollapszus, hanem a gravitációs vonzás megakadályozza
a makroszkopikus testek tömegközépponti
hullámcsomagjának felhasadását. Így a hullámcsomag
egyben maradva, klasszikus tárgyként mozog, és akadályokba
ütközve, kaotikus mozgással hoz létre véletlen
eseményeket.
Rossz hír, hogy amíg a lineáris Schrödinger-egyenlet
valamiféle hályogkovács biztonságával kerüli el a
kvantummechanikában rejlő nemlokalitás súlyosabb
bonyodalmait, a nemlineáris dinamikában ez a biztonság
összeomlik, és az elmélet építésekor fáradságos
aprómunkával kell kerülgetni a kauzalitást fenyegető buktatókat.
Hogy végülis a gravitáció erős vagy gyenge, hogy
pályamódosításon vagy interferencián keresztül befolyásolja
hatékonyabban a kvantum-klasszikus határon
zajló eseményeket, az nyitott kérdés. Itt kapcsolódhat
a történet a kvantumgravitáció területéhez: az
elmélet egyes változatai arra utalnak, hogy talán nagyon
rövid távolságokon (becsavarodott vagy lelapult
extra dimenziók méretén belülre kerülve) a gravitáció
sokkal erősebb lehet annál, mint amit a newtoni távolságskálán
megismertünk. Ennek kísérleti tesztelése
elkezdődött, de egyelőre nehéznek bizonyult a szintén
rövidtávú Casimir-erők zavaró hatása miatt.
Epilógus
- A kvantum-klasszikus határ megismerése keményebb
dió, mint atyáink gondolták.
- Több mint száz évvel Planck felfedezése, nyolcvan
évvel a természettörvénnyé vált kvantummechanika
megszületése után már igazán ideje lenne megtalálni
a biztonságos átjárást kvantum és klasszikus
között.
- Lessük a kísérleteket a senkiföldje-tömegek világából,
- addig is, gyártjuk az elméleteket.
Az itt áttekintett kérdések iránti érdeklődésemet
Fényes Imrétől kaptam; kár, hogy nem érhette meg a
témakör mai virágzását. Sok részletkérdéssel kapcsolatban
Diósi Lajossal való sűrű diszkussziók másfél
évtizede formálta a véleményemet. Külön köszönet
illeti Frenkel Andort, aki segített megérteni Károlyházi
Frigyes eredményeit.