Fizikai Szemle 2008/6. - Kun Ferenc: FRAGMENTÁCIÓS FOLYAMATOK UNIVERZALITÁSI OSZTÁLYAI

FRAGMENTÁCIÓS FOLYAMATOK UNIVERZALITÁSI OSZTÁLYAI

Kun Ferenc
Debreceni Egyetem, Elméleti Fizikai Tanszék

Meglepõ univerzalitás

Hétköznapi tapasztalat, hogy ha elejtünk egy porcelántányért, az a konyha talajához csapódva darabokra törik. Általánosan igaz, hogy egy szilárd test széttörése, fragmentációja akkor következik be, ha a testtel rövid idõ alatt nagy mennyiségû energiát közlünk. Ez elérhetõ például úgy, hogy a testre ütést mérünk egy kalapáccsal, lövedéket lövünk bele, robbanóanyaggal felrobbantjuk, vagy ha a testet ütköztetjük egy másikkal (például a talajjal). Az energiaközlés következtében egy lökéshullám jön létre, amely nagyszámú repedést hagy maga után, s e repedések mentén a test darabokra esik szét. Fragmentációs jelenségek a természetben igen széles méretskálán fordulnak elõ: a Naprendszer aszteroidáinak ütközésétõl a mikrovilág hosszú láncmolekuláinak töredezéséig mindenütt találkozhatunk velük. A közbensõ méretskálákon számos ipari alkalmazás (bányászat, nyersanyag-feldolgozás) és geológiai példa (vulkánkitörés) említhetõ.

Szilárd testek széttörése egy egyensúlytól távoli folyamat, amely rendkívül gyorsan játszódik le, így a fragmentációhoz vezetõ mikroszkopikus törési események kísérletileg nehezen hozzáférhetõek, a megfigyelések általában néhány mennyiségnek a folyamat végállapotában elõálló eloszlásaira vonatkoznak. Már egy porcelántányér vagy egy üvegpohár elejtésekor is észrevehetõ, hogy a legtöbb darab kis méretû, s a méretük növekedésével a keletkezett fragmensek darabszáma csökken. Az elmúlt évtizedekben a laboratóriumi kísérletek arra a meglepõ eredményre vezettek, hogy az egyes fragmensek méretének vagy tömegének gyakoriságát jellemzõ méreteloszlás, illetve tömegeloszlás hatványfüggvény szerint csökken, függetlenül az anyagi minõségtõl, az energiabetáplálás módjától és a releváns mikroszkopikus kölcsönhatásoktól. 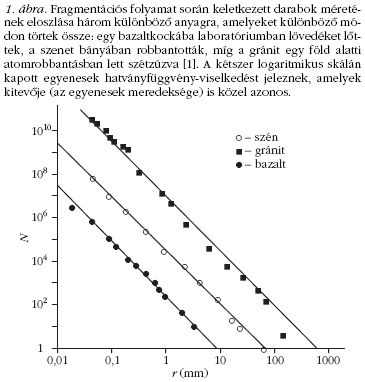Így például a nehéz atommagok ütközésekor keletkezõ kisebb atommagok töltéseloszlása ugyanúgy hatványfüggvény-viselkedést mutat, mint a bányában robbantott széndarabok tömegének, vagy a Naprendszerben keringõ, számos ütközést elszenvedett aszteroidák átmérõjének eloszlása [1].

Szilárd testek fragmentációjának beható vizsgálata további érdekes eredményekkel szolgált. Kimutatták, hogy a fragmensméret-eloszlás hatványfüggvényalakot vesz fel, ha a széttört test kellõen rendezetlen mikroszkopikus tulajdonságokkal rendelkezik (például beton, üveg, kerámia, gránit, bazalt, ....) és rideg törést mutat, azaz lineárisan rugalmasan viselkedik az eltörésig. Ilyenkor az eloszlás csökkenésének gyorsaságát jellemzõ τ hatványkitevõ értékét elsõsorban a test d dimenziója határozza meg, amelynek alapján a fragmentációs folyamatokat három univerzalitási osztályba lehet sorolni: egy dimenzióban, például vékony, hosszú üvegrudak törésekor, az exponens értéke τ ≈ 1,5; a vékony üveglapok törésével megvalósítható kétdimenziós esetben a mérések τ ≈ 1,5-2,0 eredményre vezettek, míg háromdimenziós tömbi anyagok fragmentációjakor a mért exponens τ ≈ 2,3-2,7. A tömbi anyagok fragmenseinek méreteloszlására mutat példát az 1. ábra. A fragmentációs jelenségekre megfigyelt univerzalitás megértése, a lehetséges univerzalitási osztályok felderítése máig az elméleti kutatások fõ hajtóereje [1, 2].

Szétrobbanó tartályok és az ûrszemét

Tömbszerû, egy-, két-, vagy háromdimenziós szilárd testek mellett héjszerû struktúrákat is változatos formában használunk a mindennapi életben és az iparban. Tipikus héjszerkezetek a tartályok, nagynyomású kamrák, de a repülõgépek és ûrállomásmodulok is héjszerû struktúrával rendelkeznek. Ilyen héjak dinamikus terheléssel, például robbanással szembeni stabilitása, illetve széttörésének dinamikája rendkívül fontos gyakorlati és elméleti probléma. Elméleti érdekességüket az adja, hogy lokális geometriai struktúrájuk kétdimenziós, de az anyag dinamikája három dimenzióban zajlik, ami speciális törési módusokhoz, s így a tömbanyagokétól eltérõ fragmentációhoz vezethet. Ennek ellenére héjak fragmentációjára korábban nem készültek szisztematikus kísérleti és elméleti vizsgálatok.

Héjszerkezetek fragmentációja különösen fontos szerepet játszik napjaink ûrkutatásában az ûrszemét problémájának megoldása során. Ma már széles körben használnak Föld körül keringõ mûholdakat meteorológiai, telekommunikációs, navigációs és katonai célokra. Számuk évente száznál többel növekszik, s már meghaladja a hatezret. Az elmúlt ötven év ûrkutatása során azonban nagy számban halmozódott fel a világûrben haszontalan objektum, azaz szemét is, ami komoly veszélyt jelent a mûholdakra, mert ütközéskor tönkreteheti õket. Az ûrszemét fõ forrását a föld körüli pályán történt fragmentációs események, zárt héjszerû objektumok felrobbanása jelenti. A mûholdakat pályára állító rakéták lecsatolódó üzemanyagtartályai akár évekig keringhetnek a Föld körül bennük némi maradék üzemanyaggal. Az idõ múlásával ez az üzemanyag felrobbanhat s a keletkezett hatalmas számú törmelék felhõként kering a Föld körül, ahol megsemmisítheti az útjába esõ hasznos objektumokat. A probléma komolyságát jelzi, hogy nemzetközi összefogással kiépült egy olyan radarrendszer, amelynek segítségével az összes 10 centiméternél nagyobb szemétdarabot követni lehet. A mérésekkel párhuzamosan számítógépes programokkal, szimulációkkal is követik a szemét mozgását, majd ennek megfelelõen akár napi rendszerességgel módosítják a mûholdak pályáját az ütközések elkerülése érdekében.¹ Az igazán komoly veszélyt tehát a néhány centiméteres és annál kisebb fragmensek jelentik, mert ezek annyira kicsik, hogy sem radarral, sem optikai módszerekkel nem lehet õket követni, viszont mozgási energiájuk elég nagy lehet ahhoz, hogy mûholdakat tegyenek tönkre. Ebben a mérettartományban - megfigyelések hiányában - az elméleti számolásokra kell hagyatkoznunk.

Kísérletek héjszerkezetekkel

Héjszerkezetek széttörésének és az ûrszemét problémájának megértéséhez a korábbiaknál részletesebb információra van szükségünk a fragmentációs folyamatokról. Ahhoz, hogy a törmelékdarabok föld körüli pályáját számolhassuk, megbecsülhessük a pálya várható élettartamát, illetve egy esetleges ütközés okozta károkat, ismernünk kell az egyes darabok tömegét, sebességét és alakját is.

Vizsgálataink elsõ lépéseként laboratóriumi kísérleteket végeztünk zárt héjak széttörésére. Könnyen kezelhetõ, egyszerû héjakat keresve végül meglepõ módon a tojáshéj bizonyult az egyik legkiválóbb kísérleti alanynak. Mivel a tojáshéj anyaga egy biokerámia, amely rendezetlen mikroszkopikus tulajdonságokat mutat és ridegen törik, egyedülálló lehetõséget nyújt héjszerkezetek fragmentációjának tanulmányozására. A kísérletekhez a tojás tartalmát két szabályos lyukon keresztül kifújtuk, majd az üres héjat kimostuk és kiszárítottuk. Annak tisztázására, hogy a héjszerkezet anyagi tulajdonságai hogyan befolyásolják a fragmentációs folyamat eredményét, a kísérleteket elvégeztük több különbözõ típusú tojáshéjjal (tyúk- és fürjtojással), továbbá mûanyag- és üveggömbökkel is. A rideg törés biztosítására a mûanyag-gömbhéjakat folyékony nitrogénben lehûtöttük.

Az energia betáplálására két módszert alkalmaztunk: vizsgáltuk a héj ütközés és robbanás okozta fragmentációját. Az ütközéses kísérletekhez egy katapultot építettünk, amellyel a héjakat a kemény talajba lõttük. Robbantáshoz durranógázt használtunk, azaz a héjakat hidrogén és oxigén 2:1 arányú keverékével töltöttük fel, majd távirányítással, elektromos gyújtással indítottuk a folyamatot. Mindkét fragmentációs folyamat egy nagyméretû, puhafalú mûanyagzsákban zajlott, hogy minimalizáljuk a környezet zavaró hatását. Lehetõségünk nyílt a robbantási kísérleteket az Oslói Egyetem Fizikai Intézetének nagy sebességû jelenségekkel foglalkozó laboratóriumában is elvégezni, ahol speciális nagy sebességû kamerák segítségével sikerült a héjak széttörési folyamatáról mélyebb információt szereznünk.

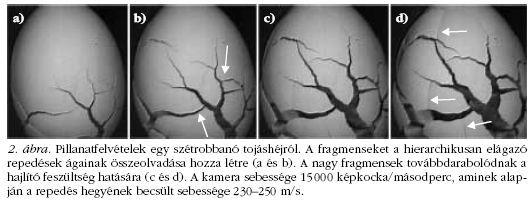
A 2. ábrán a tojáshéj robbanási folyamatáról készült pillanatfelvételek láthatók. A felvételek elemzésével arra a megállapításra jutottunk, hogy a héjak feltörésének dinamikája két jól elkülönülõ lépésre bontható. Megfigyelhetõ, hogy a fragmentáció egy repedés megjelenésével indul a tojás laposabb oldalán, ahol a héj vékonyabb és gyengébb. A tojáshéj tágulása miatt a héjfelületen jelentõs húzófeszültség ébred, amelynek eredményeként a repedés nagy sebességgel halad a képen felfelé. A héj anyagának rendezetlen mikroszkopikus tulajdonságai és a viszonylag nagy sebesség miatt a repedés instabillá válik és elágazik, majd az így megnövekedett energiadisszipáció lelassítja és stabilizálja a repedés új ágait. A héj tágulása miatt aztán ezek a mellékágak növekvõ sebességgel terjednek, ezért ismételt instabilitás és elágazás jöhet létre. Így tehát a tágulás okozta húzófeszültség eredményeként létrejövõ elsõdleges repedések egy hierarchikusan elágazó, faszerû struktúrát hoznak létre. A fragmensek a repedési fa mellékágainak összeolvadásával jönnek létre, amire a 2.b ábrán a nyilak mutatnak példát. A fragmentációs folyamat második szakaszában már a hajlító feszültség játszik szerepet, amelynek hatására a héjdarabokban másodlagos repedések jönnek létre a korábbi elsõdleges repedésekre merõlegesen (a 2.d ábrán a nyilak jelzik ezeket). Fontos megjegyezni, hogy a tojáshéjdarabok alakja jó közelítéssel izotróp, erõsen elnyúlt fragmensalakot sosem figyeltünk meg. A tojáshéj fragmentációjának fent bemutatott folyamata egy általános mechanizmus, amely erõsen rendezetlen, rideg anyagok széles osztályára érvényes.

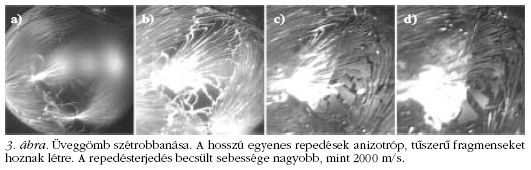
Üveggömbökkel végzett kísérleteink kimutatták, hogy az elsõdleges repedések dinamikája erõsen függ az anyagi tulajdonságoktól. Az üveg mechanikai teherbíró képessége és Young-modulusza sokkal nagyobb a tojáshéjénál, míg a mikroszkopikus rendezetlenség és a rugalmas hullámok csillapítása jelentõsen kisebb. Ennek következményeként üvegben a repedések sokkal nagyobb sebességgel terjednek, és viszonylag nagy távolságot tudnak megtenni elágazás nélkül [3, 4]. Ahogy a 3. ábrán megfigyelhetõ, az üveggömb elsõdleges repedései egyenesek, amelyek a héj véletlenszerûen elhelyezkedõ leggyengébb pontjaiból indulnak ki. A repedések nem ágaznak el, így az elsõdleges repedések nagy számú, vékony, hosszú, tûszerû fragmenst eredményeznek, amelyek instabilak a hajlítással szemben. A másodlagos repedések a tûszerû fragmenseket tovább darabolják.

Zárt héjak univerzalitási osztálya

A mérési adatok kvantitatív kiértékeléséhez a fragmenseket egy nyitott scannerrel digitalizáltuk, így minden egyes robbantási és ütközési kísérlet eredményét egy fekete-fehér képpé tudtuk alakítani. A képeken a fragmensek fekete foltként jelentek meg a fehér háttéren, amelyeket egy klaszterkeresõ programmal azonosítottunk. Az egyedi fragmenseket három mennyiséggel jellemeztük: a fragmens m tömegét a folt pixeleinek számával definiáltuk, a fragmens A felszíne a folt kontúrvonalának hossza, az R_g girációs sugarat (a fragmens átlagos sugarát) pedig a folt m pixeleinek r_i helyvektoraiból számítottuk ki. A jó statisztika eléréséhez a kísérleteket azonos körülmények között nagy számú mintadarabbal megismételtük: összesen körülbelül 300 darab tojást, továbbá 200 darab mûanyag- és üveggömböt használtunk fel. Az egyes mennyiségeknek a továbbiakban bemutatandó eloszlásfüggvényei 40-50 fragmentációs eseményre voltak átlagolva. Egy robbantási, illetve ütközési kísérletben tipikusan néhány száz, illetve néhány ezer fragmens keletkezik.

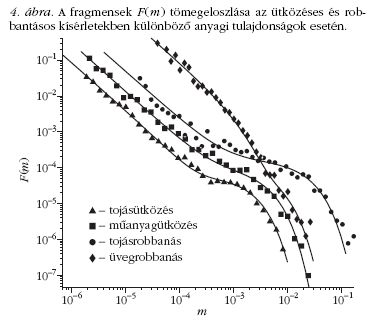
A 4. ábrán a fragmensek F(m) tömegeloszlása látható különbözõ anyagból készült héjak esetén az ütközési és robbantási kísérletekben. A mérések egyik legfontosabb eredményeként azt kaptuk, hogy a kis fragmenstömegek tartományában az egyes eloszlások hatványfüggvény-viselkedést mutatnak, amelynek exponense hibahatáron belül megegyezik az egyes esetekben. Az eloszlásfüggvények között különbség csak a nagy fragmensek tartományán észlelhetõ. A függvényillesztések alapján a τ exponens értékére τ = 1,35±0,05 adódott, függetlenül a héj anyagi minõségétõl és az energia betáplálásának módjától. Összevetve az irodalomban található eredményekkel, a héjakat jellemzõ exponens szignifikánsan különbözik a két- és háromdimenziós tömbi anyagokra mért exponensektõl, ami egyértelmûen a zárt héjak speciális széttörési mechanizmusának következménye. Az exponens értéke alapján a zárt héjak széttörése a fragmentációs jelenségeknek egy újszerû univerzalitási osztályát adja [2-4].

Tömbi anyagok fragmentációs kísérletei során a fragmensek alakja mindig izotrópnak bizonyult, azaz sosem figyeltek meg elnyúlt, erõsen anizotróp fragmensalakokat. Héjak esetén viszont láttuk, hogy az anyagi minõségtõl függõen a héjfragmensek alakja az izotróptól az erõsen anizotróp, tûszerû formáig változhat. Annak jellemzésére, hogyan változik a fragmensek alakja a méretükkel, meghatároztuk a fragmensek <m> átlagos tömegét az R_g girációs sugár függvényeként. 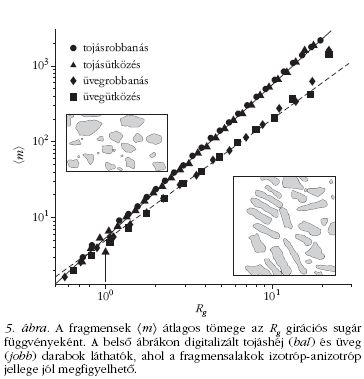Az 5. ábrán látható, hogy minden egyes héjtípus és energia-betáplálás esetén hatványfüggvényt kapunk eredményül, de az exponens értéke jelentõsen függ az elsõdleges repedésmintázat szerkezetétõl. Mivel a tojáshéjdarabok viszonylag szabályos, izotróp alakúak, tömegük a girációs sugár második hatványával arányos, azaz α = 2,0±0,05 értéket kaptunk illesztéssel. A nagyméretû üvegdarabokra szignifikánsan kisebb az exponens α = 1,5±0,08, viszont a kisebb méretekhez közeledve üveg esetén is átmenetet kapunk az izotróp fragmensalakhoz α = 2,0±0,08 kitevõvel. Az átmeneti fragmensméretet az 5. ábrán a nyíl jelöli [4]. Az α < 2 exponens azt jelzi, hogy az üvegfragmensek önaffin tulajdonságúak, azaz minél nagyobbak, annál elnyúltabbak. Hasonló önaffinitást tömbi anyag fragmenseire sosem figyeltek meg, ez a fragmentálódó héjszerkezetek törési mechanizmusainak következménye [4].

Számítógépes szimulációk

Héjszerkezetek fragmentációjának elméleti leírására kidolgoztunk egy realisztikus, háromdimenziós modellt, amelynek keretében molekuláris dinamikai szimulációkkal vizsgáltuk zárt héjak felrobbanását és kemény fallal történõ ütközését. A modellben egy gömbhéjat diszkretizáltunk - mezoszkopikus méretû elemekre bontottuk - úgy, hogy a gömb felszínét véletlenszerû háromszögekkel fedtük le. A háromszögek csúcspontjaiba tömeggel rendelkezõ részecskéket helyeztünk, amelyeket a háromszög élei mentén rúdelemekkel kapcsoltunk össze. Egy robbanási folyamat szimulációja során a gömböt gázzal töltjük fel, amely a nyomástól függõ erõt fejt ki a modell diszkrét elemeire. A rendszer idõfejlõdését a részecskék klasszikus mechanikai mozgásegyenleteinek numerikus megoldásával állítjuk elõ. A fragmentációs folyamat során fellépõ tágulás eredményeként a részecskéket összekötõ rudak deformálódnak. Ha a deformáció a szimulációban átlép egy véletlenszerû küszöbértéket, a rúdelem eltörik, és egy repedés keletkezik a gömb felszínén. A 6.a ábrán egy robbantási folyamat szimulációjának eredménye látható, ahol a fekete pöttyök a mikrorepedéseket jelölik. A szétrepülõ darabokat visszahelyeztük eredeti helyükre, így a gömb felszínén jól megfigyelhetõk a fragmensek.

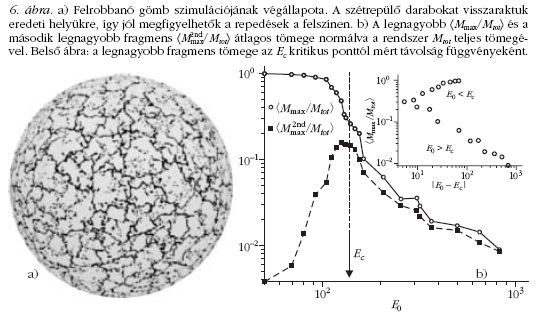
Számítógépes szimulációkat végeztünk széles tartományon változtatva a robbanás kezdeti nyomását és az ütközés energiáját. A fragmentációs folyamat végállapotának jellemzéséhez meghatároztuk a legnagyobb és a második legnagyobb fragmens tömegét a kontrollparaméter (nyomás, illetve betáplált energia) függvényeként. A 6.b ábrán jól látható, hogy amíg kicsi a betáplált energia, a legnagyobb fragmens tömege közel megegyezik a rendszer teljes tömegével, míg a második legnagyobb fragmens nagyságrendekkel kisebb. Ez azt jelenti, hogy alacsony energián a héj megrepedezik, a repedések mentén kiszáll némi por, de a rendszer megõrzi integritását. Ezen az energiatartományon tehát nem beszélhetünk fragmentációról, a héj csak károsodást szenved. A számítógépes szimulációk megmutatták, hogy a fragmentáció eléréséhez a betáplált E₀ energiának át kell lépnie egy E_c kritikus értéket, amikor a legnagyobb és második legnagyobb fragmens összemérhetõvé válik, majd együtt csökken. A 6.b ábra belsõ kis ábráján a legnagyobb fragmens tömege látható az E_c kritikus ponttól mért távolság függvényeként. A kétszer logaritmikus skálán kapott jó minõségû egyenesek hatványfüggvény- viselkedésre utalnak. Ez azt jelzi, hogy az energia növelésével a károsodott fázisból a fragmentált fázisba történõ átmenet a másodrendû fázisátalakulásokhoz hasonló módon következik be.

A fragmentált fázisban, azaz E₀ > E_c esetén, a fragmensek tömegeloszlása a szimulációkban is hatványfüggvénynek adódik τ = 1,35±0,06 exponenssel, ami nagyon jól egyezik a méréseinkkel [3, 4]. A szimuláció paramétereit egyetlen konkrét anyaghoz sem illesztettük, így a kísérletekkel való egyezés a héjszerkezetek univerzalitási osztályának robusztusságát is jelzi [3]. Analitikus számításokkal sikerült megmutatni, hogy az önaffin fragmensalak a hajlítási feszültség miatt fellépõ másodlagos fragmentáció következménye. Így érthetõ, miért nem lehet önaffinitást tömbi anyagok fragmenseire megfigyelni [4].

Összefoglalás

A rendezetlen mikroszkopikus szerkezetû, ridegen törõ szilárd testek fragmentációs folyamatai meglepõ univerzalitást mutatnak: a keletkezett darabok méret-, illetve tömegeloszlása hatványfüggvény szerint csökken, amelynek exponense elsõsorban a dimenziószámtól függ. Vizsgálataink eredményeként kiderült, hogy a zárt héjszerkezetek fragmentációja során keletkezõ darabok tömegeloszlása és alaki jellemzõi is eltérnek a tömbi anyagokétól. Héjszerkezetek fragmentációja egy önálló univerzalitási osztályt alkot, ami a héj speciális törési mechanizmusainak következménye. A NASA és az Európai Ûrhivatal (ESA) által a Föld körül keringõ ûrszemét követésére kifejlesztett szimulációs programok nem modellezik a szemetet keltõ robbanási folyamatot, csak a törmelékfelhõ idõfejlõdését határozzák meg. A szimulációs programokba tehát be kell táplálni a fragmentációs folyamat eredményét, azaz a fragmensek tömegét, méretét, alakját és sebességét jellemzõ valószínûségeloszlásokat. A bemutatott eredményeket ûrszemétszimulációs programokba beépítve növelhetõ az ûreszközök biztonsága [5].

Irodalom

D. L. Turcotte: Fractals and chaos in geology and geophysics. Cambridge University Press, 1997.
F. Kun, H. J. Herrmann, Physical Review E 59 (1999) 2623.
F. K. Wittel, F. Kun, H. J. Herrmann, B.-H. Kröplin, Physical Review Letters 93 (2004) 035504.
F. Kun, F. K. Wittel, H. J. Herrmann, B.-H. Kröplin, K.-J. Maloy, Physical Review Letters 96 (2006) 025504.
J. Hogan: Exploding eggshells could reduce space junk risk. New Scientist (2004) 2456.

________________________

¹ A NASA Space Debris Department nyilvántartása szerint eddig a világurben 178 darab robbanás történt, a folyamatosan követett törmelékdarabok száma közel 200 000.

Fizikai Szemle honlap