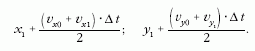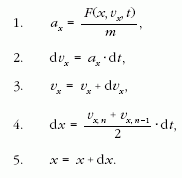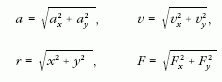Fizikai Szemle 2008/9. 311.o.
FIZIKÁZZUNK EGYSZERŰEN, SZÁMÍTÓGÉPPEL
Eichhardt Iván, Jaloveczki József
Mandelbrot Tudományos Diákkör
Szent László ÁMK, Baja
Közismert, hogy a diákok szeretnek számítógéppel
játszani. Szerencsére ma már sok gyereknek van otthon
is gépe, de akiknek nincs, azok is hozzáférhetnek
az iskolában. Az is közismert, hogy többségük nemigen
szereti a fizikát, matekot. E tantárgyak megkedveltetéséhez
szeretnénk a PC népszerűségét felhasználni.
Szinte játékosan lehet Newton törvényeit, a
mozgások leírását megtanulni, emellett számos függvényábrázolást
és a függvények tulajdonságait megismerni.
Programunk egy pontszerű test egy- és/vagy
kétdimenziós mozgását modellezi. Az Excel-program
a megadott paraméterek alapján dt időközönként
számolja a test hely, sebesség, gyorsulás adatait, majd
ezeket ábrázolja az idő függvényében. Kétdimenziós
mozgásnál az a gyorsulást, a v sebességet és az r helyet
az x és y komponensekből számolja Pitagorasz
tételével.
Érdekes lehet a testre ható eredő erő hely szerinti
változása, amit szintén megtekinthetünk a program
futása során. Kétdimenziós mozgásnál nagyon szemléletes
a pályagörbe (x−y sík) kirajzolása. Megnézhetjük
a fázissíkbeli ábrát is, ami nem más, mint a hely
(x, y vagy r ) − sebesség (v) grafikon. Az ilyen ábrázolást
főleg a periodikus mozgásoknál és a gerjesztett,
súrlódásos eseteknél érdemes tanulmányozni. Utóbbiaknál
a mozgás kaotikusságát is el lehet érni, ami jól
látszik azon, ahogyan a test mozgása alakul a kezdeti
feltételek kis változásaira.
Néhány kipróbálásra érdemes esetet mutatunk be
az egészen egyszerűtől a bonyolult erőtörvényig. Az
egyes eseteken belül számtalan kezdeti paraméterértékkel
lehet játszani. A játékkal jól fejleszthető a dinamikai
szemlélet, fejleszti a matematikai és informatikai
kompetenciákat is. A program jól használható a
középiskolai 9. évfolyamos fizikaoktatásban az erő-
sebesség (m/s)
törvények tanításánál, érettségire előkészítő órákon,
szakkörökön és azon kívül is bármikor.
A programban szereplő általános erőtörvényt egydimenziós
esetben skalárként, illetve kétdimenziós
esetben már vektorként kezelve az alábbiakban foglalhatjuk
össze:
F = F0 − D · l − µ · m · g − k · v − C · v2 + A · cos(ωt + φ) .
Tehát a testre ható F erő állhat egy F0 állandó irányú
és nagyságú erőből, egy Dl alakú rúgóerő típusú erőből,
ahol D a rugóállandó, l pedig a rugó megnyúlása
a nyugalmi hosszához képest, továbbá disszipatív
tagokból, mint a µmg súrlódási erő (µ a súrlódási
együttható, m a test tömege, g a nehézségi gyorsulás),
és a sebességtől függő közegellenállási erőkből (kis
sebességeknél ez lineáris, együtthatóját k -val jelöltük,
míg nagy sebességeknél v2-tel arányos, együtthatóját
C-vel jelöltük), befejezésképpen még tartalmaz egy
periodikus kényszererőtagot (amplitúdója A, körfrekvenciája
ω és relatív fázisa φ).
A program futtatásához meg kell adni a kezdőadatokat,
a beviteli mezőben lévő cellák tartalma:
E5: időköz
G5: a választott időközhöz kiszámolja, hogy az
intervallumban milyen a sebességnövekedés (%-ban)
és az összes érték közül a maximálist írja ki. Célszerű
úgy választani időközt, hogy ez az érték az 5%-ot ne
haladja meg. A közelítés akkor még jónak vehető.
K5: tömeg
B6: Az x irányú periodikus erő körfrekvenciája
B7: Az x irányú periodikus erő kezdőfázisa
B8: Az x irányú periodikus erő amplitúdója
D6; D7; D8: a fenti háromnak felel meg csak az y
irányra
F6; H6: a sebesség négyzetével arányos közegellenállás
tényezője (y és x irányra)
E8; H8: a sebességgel egyenesen arányos közegellenállás
tényezője (y és x irányra)
E7; H7: A testre ható állandó erő (y és x irányú
komponensek)
L6; N6: a test kezdeti helykoordinátái (y0 és x0)
L8; N8: a testre ható súrlódási erő (vízszintes felületen,
gravitációs mezőben) felületi tényezői (y és x irányokban)
Q5; Q10: a test kezdeti sebessége (x és y irányokban)
P6; P11: a testre ható rugalmas erő direkciós ereje
(x és y irányokra)
Q8; Q13: a testhez kapcsolt rugó nyújtatlan hossza
(x és y irányokban)
A program a szükséges paraméterek (tömeg, súrlódás,
közegellenállási tényezők stb.) bevitele után a
kezdeti hely- és sebességadatokból az erőtörvény
alapján kiszámolja az erő (x, y) komponenseit (L19;
M19). Ezekből (a tömeg figyelembe vételével) a gyorsulásokat
(C19; D19). Ezeket az adott intervallumban
állandónak tekintjük. A gyorsulások ismeretében
meghatározza az új sebességeket (v0+aΔt alapján,
F20; G20), majd ezekből trapézközelítéssel (az intervallumra
átlagsebességet véve) az új x és y értékeket:
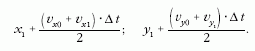
Így kicsit pontosabb, mint ha az intervallum elején vett
sebességgel számolnánk. Az első hely-, illetve sebességkoordináták
a felhasználó által megadott kezdeti
értékek (L6; N6; Q5; Q10). Az új sebesség- és helykoordinátákkal
az erőtörvényből újabb erőkomponenseket
számol (L20; M20) és így tovább körülbelül 20 000 lépésben.
A mozgás teljes ideje a lépések száma szorozva
a dt intervallummal. Közben a gyorsulás nagyságát
(E19) és az erő nagyságát (N19) is kiszámolja, valamint
az r helyet a komponensekből, Pitagorasz-tétellel.
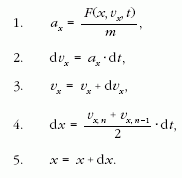
Az 1. egyenletben Newton II. törvénye alapján
számoljuk az x irányú gyorsulást. Az erő függhet a test
helyétől és sebességétől, valamint az időtől. Speciális
esetben az erő állandó.
A 2. összefüggés a sebességváltozás (x irány) az
adott intervallumban.
A 3. egyenletben az intervallum elején lévő sebességhez
hozzáadjuk a változást, így megkapjuk az időszakasz-
végi sebességet (x irányra).
A 4. egyenlet az adott időszakaszban történt x irányú
elmozdulást számolja trapézközelítéssel.
Végül az 5. egyenlet az eredeti hely x értékét korrigálja
a kis elmozdulással.
Az y irányú jellemzők kiszámítása teljesen hasonló
egyenletekkel történik. Az iterációs eljárást kétdimenziós
mozgásnál mindkét irányra elvégzi a program
körülbelül 20 000 lépésig (n), azaz a mozgás nyomon
követhető t = n · dt ideig.
Valamint érvényesek még az
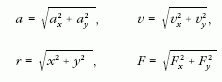
összefüggések is.
Most nézzünk néhány példát.
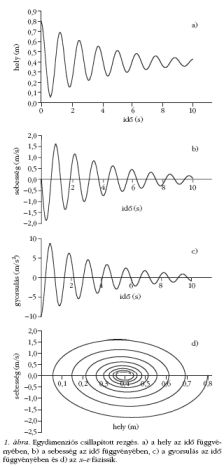
Egydimenziós, csillapított rezgés
Az erőtörvény: F = −Dx · (l0x − x) − kx · vx.
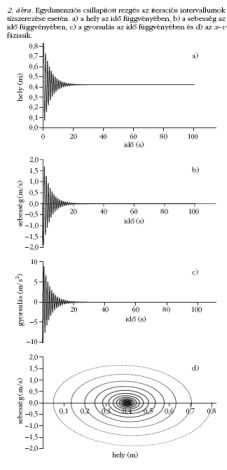
Az 1. ábrán jól látható ahogy a test mozgása csillapodik.
A mozgás kezdeti feltételei: a test m tömege 2
kg, kezdeti x0 kitérése 0,8 m, a Dx rugóállandó 50
N/m, a kezdeti l0x rugóhossz 0,4 m és a kx
közegellenállási
tényező 1. A számolást dt = 0,0005 s időintervallumokra
végeztük 20 000 lépésben.
A 2. ábrán ugyanaz a mozgás látható az iterációs
intervallumok tízszerezésével, így a megfigyelt mozgás
ideje is tízszeresére növekedett, az időtartam végén
szinte nyugalomba került a test.
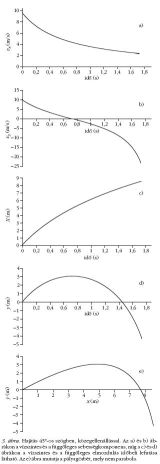
Hajítás 45°-os szögben, közegellenállással
Az erőtörvény: Fx = − Cx · v2x
és Fy = mg − Cy · v2x.
A 3. ábra jól mutatja, hogy a közegellenállásos
hajításnál a sebesség nem egyenletesen változik, a
pályavonal nem parabola. A mozgás kezdeti feltételei:
a test m tömege 2 kg, kezdősebességének komponensei:
v0x = v0y = 10 m/s, a közegellenállási
tényező:
|Cx| = |Cy| = 0,3 és a közegellenállás természetesen
mindig lassítani igyekszik a test mozgását. A számolást
dt = 0,0008 s időintervallumokra végeztük 20 000
lépésben.
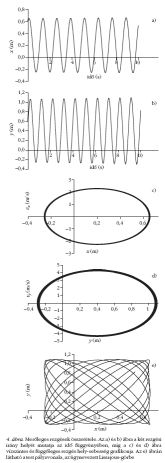
Merőleges rezgések összetétele, Lissajous-görbe
Az erőtörvény: Fx = −Dx · (l0x − x) és
Fy = −Dy · (l0y − y)
A pontszerű test egyidejűleg végez rezgőmozgást
egymásra merőlegesen, eltérő amplitúdóval és frekvenciával
(4. ábra). A mozgás kezdeti feltételei: a
test m tömege 2 kg, kezdeti x0 és y0 kitérése egyaránt
0,6 m, kezdősebessége v0x = 1 m/s, valamint
v0y = 4 m/s, a rugóállandó komponensei
Dx = 50 N/m, míg
Dy = 80 N/m,
a kezdeti rugóhossz l0x = 0,2 m, illetve
l0y = 0,4 m. A számolást dt = 0,0005
időintervallumokra végeztük 20000 lépésben.
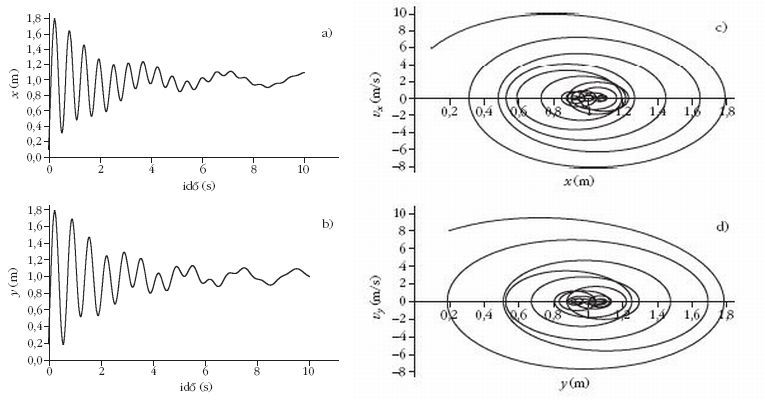
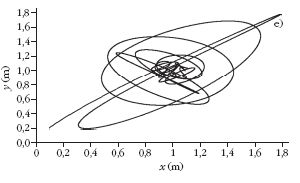
Kétdimenziós, csillapított és gerjesztett rezgés
E mozgás erőtörvényében csak a súrlódási tag hiányzik
az általános erőtörvényben leírtakból. Az 5. ábrán látható
mozgás kezdeti feltételei: a test m tömege 1 kg,
kezdeti x0 és y0 kitérése egyaránt 0,1 és 0,2 m,
kezdősebessége
v0x = 6 m/s, valamint
v0y = 8 m/s, a rugóállandó
komponensei Dx = 120 N/m, míg
Dy = 90 N/m, a kezdeti
rugóhossz l0x = l0y = 1 m.
A gerjesztő erő jellemzői:
körfrekvenciája: ωx = 2 Hz és
ωy = 3 Hz,
fázisa: φx = 5°
és φy = 3°,
míg amplitúdója: Ax = 10 N és
Ay = 7 N. A
közegellenállási tényezők: |Cx| = 0,2 és
|Cy| = 0,1,
valamint kx = ky = 1. A számolást dt = 0,0005 s
időintervallumokra
végeztük 20 000 lépésben. A pályagörbét
szemlélve a mozgás kaotikusnak tűnik.
Véletlenszerűen beállított értékekkel számtalan
érdekes “kaotikus” ábrát kaptunk. A fentebb felsorolt
esetektől eltérő beállításokkal is lehet próbálkozni. Jó
szórakozást kívánunk diáknak, tanárnak egyaránt!
Készítettünk egy kis animációs programot (rugó.exe),
ami beállítható paraméterekkel mutatja be a mozgást.
Ehhez azonban segédprogram telepítése is szükséges.
Mindkettő megtalálható és letölthető a
http://www.karolyireneusz.extra.hu/e107/download.php?list.3
címen. Ugyanitt megtalálható az Excel-program dinamika
néven. Hozzászólásokat, véleményeket és kérdéseket
szívesen fogadunk a jalo@freemail.hu címen.