
Fizikai Szemle honlap |
Tartalomjegyzék |
Patkós András
ELTE, Atomfizika Tanszék
T dS = dE + p dV.
Itt T a test hőmérséklete, p a nyomása, dE a rendszer belső energiájának, dV a térfogatának infinitezimális megváltozása. A mechanikai munkavégzés és a belső energiaváltozás eredőjeként adódó infinitezimális hőcserét az entrópia dS megváltozása kontrollálja. Az entrópia ezen bevezetése Rudolf Clausius műve. Az első lépést megtevő S. Carnot és Clausius (1. kép ) nyomán a fizikusok a hőerőgépek hatásfoka növelésének feladatára koncentráltak, és az entrópiát elsősorban a munkává alakítható energiában bekövetkező veszteség szempontjából vizsgálták. Clausius mondta ki a mechanika törvényeire vissza nem vezethető állítást, miszerint zárt rendszerben az entrópia egyetlen természeti folyamatban sem csökkenhet:dS ≥ 0.
A kvázisztatikus hőcsere egyenletének integrálásával meghatározható egy folyamatfüggetlen, valamint a mechanikai és elektromágneses állapothatározóktól is független makroszkopikus állapothatározó, az entrópia:S = S (E,V) + S0.
Ennek integrációs állandóját a harmadik főtétel nullára rögzíti az abszolút hőmérsékleti skála nullapontjában. A termodinamika a nem-redukcionista (azaz a jelenségeket kisebb alkotórészek közötti folyamatokra visszavezetni nem kívánó) fizika nagyszerű teljesítménye. A redukcionista megközelítéstől való tartózkodás az az erény, amely egyéb, összetett nem-fizikai rendszerek (gazdaság, társadalmi szervezet stb.) kutatóit arra ösztönözte, hogy saját területükön analóg leírást keressenek, egyszerű szabadsági fokokat azonosítsanak, és egyenlőtlenség-alakú, változási irányt jelző összefüggésre jussanak. Megemlíthető Nicholas Georgescu- Roegen (2. kép ), aki 1971-ben publikálta Az entrópiatörvény és a gazdasági folyamat című könyvét. Ez a könyv nagy hatással volt az ökológiai gazdaságtan irányzatának létrejöttére, amely a természeti és emberi erőforrásokkal létrehozható gazdasági értéket az erőforrások állapotának reprodukálása mellett kívánja optimalizálni. A termodinamikusok mindmáig élénk vitája a termodinamika második főtételéhez vezető axiómák pontos megfogalmazását, a törvény alá vetett folyamatok egyértelmű körülhatárolását célozza. Ebben a tisztázó folyamatban Max Planck is aktívan részt vett, többek között 1897-ben kiadott tankönyvével, valamint a termodinamika harmadik tételének és az abszolút hőmérséklet fogalmának elfogadtatásáért tett erőfeszítéseivel. Érdemes felfigyelni arra, hogy még élete végén írott tudományos életrajzában [1] is hangsúlyozza, hogy milyen nehézségbe ütközött a Carnot-ciklus levezetésére használt, a kalorikumelméletet tükröző eredeti vízimalom-hasonlatnak (3. kép ) kiszorítása a fizikusok gondolkodásából. A termodinamika redukcionista megközelítése a Ludwig Boltzmann által javasolt statisztikus mechanikai megalapozással jelentkezett, amelynek lényegét éppen Planck öntötte tömör, és a mechanikai rendszerekről továbblépő általánosítást lehetővé tevő formába:SN = kB ln WN,
ahol kB = 1,38 · 10-23 J/K. A kulcskérdés a WN mennyiség meghatározásának, azaz egy rendszer valamely rögzített belső energiájú makroállapotát megvalósító mikroállapotok leszámolásának mozzanata. Ez a lépés két kritikus kérdést hordoz magában. Az első: az adott állapot szempontjából alapvetőnek tekinthető alkotórészek (szabadsági fokok) azonosítása. A második: a szabadsági fokok diszkretizálása, ami leszámlálhatóságuk előfeltétele. A termodinamikus Planck sokáig kritikusan vélekedett a mechanika időtükrözésre szimmetrikus törvényeit a valószínűségi megközelítéssel ötvöző statisztikus mechanikai irányzat és a termodinamika összekapcsolhatóságáról. Szerepet játszott a molekuláris rendezetlenség kiegészítő fogalmának kialakításában, amely a mechanika törvényein túllépő feltétel a folyamatok időirányának meghatározottságára vezető H-tétel alkalmazhatóságára. Tudományos felfogásában ezért igazi személyes fordulatnak tűnik, hogy az elektromágneses térrel termikus egyensúlyban lévő abszolút fekete test sugárzási spektrumának értelmezéséhez a Boltzmann-féle valószínűségi entrópiafogalomra épülő elméletet dolgozott ki. Ebben a jelenségben is, mint a termodinamika egész konstrukciójában, valószínűleg az univerzalitás ragadta meg. Ma ezt úgy fogalmazhatjuk, hogy a hőmérsékleti sugárzás spektruma független attól, hogy a laboratóriumban gondosan hőszigetelt, tükröző falú tartály belsejében elhelyezkedő szénszemcse sugárzása, vagy a Világegyetem egészét kitöltő elektromágneses állóhullámok valósítják-e meg. E felismerés alapján Planck a végeredmény szempontjából közömbös modellrendszert választott: egyetlen, elektromosan töltött harmonikus oszcillátor kölcsönhatását vizsgálta az abszolút fekete testet megvalósító üregrezonátor elektromágneses állóhullámaival. Termodinamikusként eltért kortársai megközelítésétől, amely közvetlenül az üreg/oszcillátor kis frekvenciatartománybeli energiasűrűségének meghatározására irányult. Tudván, hogy az entrópia a rögzített térfogatú rendszerben az energiának egyértelmű függvénye, N darab frekvenciájú oszcillátor halmazára érvényes entrópia-energia összefüggés megalkotását tűzte ki céljául. Boltzmann fenti képletét használta kiindulásul. A feladat N oszcillátor NE összenergiájú makroállapotához tartozó mikroszkopikus állapotok WN számának meghatározása volt. Erre irányuló próbálkozásai során, a leszámlálhatóság biztosítására folyamodott az energiakvantálás „kétségbeesett” feltevéséhez:N E = Pε
. Itt ε a kvantált energiacsomag nagysága, P pedig a teljes energia csomagokba osztásával adódó csomagszám. Nagyon nagyszámú oszcillátorhoz nagyon nagy P érték kell. Ebben a határesetben Stirling képlete segítségével értékelte ki WN kombinatorikai képletét, amellyel eljutott az egyetlen oszcillátor entrópiájának képletéhez: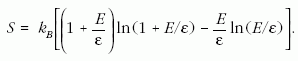
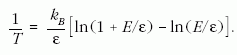
ε = h
arányosságot. Közismert, hogy Planck jelentős, de hiábavaló erőfeszítést tett az energiakvantálási feltételtől való megszabadulásra. Ez a törekvés érthető, hiszen a fentiek szerint ő pusztán a szabadsági fokok (a mikroállapotok) megszámlálhatósága érdekében diszkretizálta az oszcillátorhalmaz energiáját. Einstein és követői a legkülönfélébb anyagi rendszerek elemi oszcillátorként viselkedő szabadsági fokaira alkalmazták a kvantálás eljárását. A szilárd testek fajhőjétől a fényingadozások statisztikájáig siker sikert követett. Az entrópia megszületésétől a sugárzás entrópiájáig vezető, fél évszázadot átfogó történet összefoglalásául idézni kívánom Varró Sándor kommentárját [2], amelyet Max Plancknak az 1911-es Solvay-konferencián tartott előadására alapozott: „Az energia kvantáltságának gondolata Boltzmann-nak 1872-ben és 1877- ben megjelent munkáira vezethető vissza. Bár Boltzmann pusztán matematikai eszköznek tekintette a diszkrét elemi energiacsomagokat, mégis második cikkében - amelyben elvégezte a (termodinamikai) valószínűség kombinatorikai elemzését és kiszámította annak maximumát, megkapta a gáz molekulái által hordozott energiacsomagok (Bose-)eloszlását. Planck megjegyezte, hogy a kombinatorikus megvalósítások teljes száma, illetve azok maximális valószínűséggel bekövetkező konfigurációinak száma között a különbség elhanyagolható lévén, Boltzmann eredménye egyezik az ő entrópiaképletével.”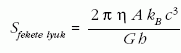
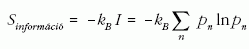
dMfekete lyuk = T dSfekete lyuk.
Ezzel viszont hőmérséklet is értelmezhető a fekete lyukakra. A Schwarzschild-megoldás szerint ugyanis egy nem-forgó fekete lyuk Bekenstein-entrópiája a tömeg négyzetével arányos. Ezért a fenti képlet alján a fekete lyuk Hawking-hőmérséklete annak tömegével fordított arányban változik. Az egyensúlyi állapotot egy statisztikus mechanikai rendszerben a kezdeti állapottól független, univerzális eloszlású állapot jellemzi. Az egyensúlyból kitérített rendszerek tapasztalat szerint véges idő alatt relaxálnak az egyensúlyi állapotba. Miután a fekete lyuk hőmérsékleti sugárzása egyensúlyi jellege miatt a korábbi (a lyukba való behullás előtti) információt „elfelejti”, Hawking feltételezte, hogy az elemi kvantumfolyamatokra érvényes úgynevezett unitaritási tulajdonság (az együttes valószínűség megmaradása) sérül. Erre kötött fogadást Kip Thorne-nal és John Preskill - lel (5. kép ) valamikor a hetvenes évek végén, amire még visszatérünk. A fekete lyukak előfordulási gyakorisága és jellemző tömege alapján az általuk hordozott entrópiára könnyen kapható becslés. Csillagászati megfigyelések alapján gyanítható, hogy minden galaxismagban, akárcsak a mi galaxisunkban, egy szupermasszív, a Nap tömegének tízmilliószorosát tartalmazó fekete lyuk helyezkedik el. Az Univerzum belátható részében található galaxisok számát 1011-re becsülik. Bekenstein képletét alkalmazva a fekete lyukak teljes entrópiájára az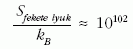
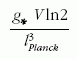
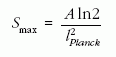
S ≈ R3 T3, E ≈ R3 T4
arányosságok. Miután az energia nagyságát korlátozza a fekete lyuk kialakulásának esélye:E ≤ állandó · R
ezért a relativisztikus részecskék gázának hőmérsékletére adódik aT ≤ állandó · R-1/2
nagyságrendi korlát. Itt az állandó tényezők konkrét értéke érdektelen, mivel csak a geometriai méretektől való függés jellegét kívánjuk megérteni. Ezt az entrópiatartalom képletébe helyettesítve látható, hogyS ≤ állandó · R3/2 ≈ A3/4
Érdekfeszítő kérdés, mi történik az éppen fekete lyukká alakuló anyag téridő szerkezetével, esetleg mikroállapotainak számával, amelynek eredményeként az entrópia a felülettel lineáris arányossági kapcsolatra vált át. A fent ismertetett gondolatok abban a megállapításban foglalhatók össze, hogy a gravitációs stabilitás korlátozza a valamely tértartományban tárolható maximális információtartalmat. A termodinamikai, statisztikus fizikai és informatikai entrópiafogalmak összekapcsolódásának felismerése vezethette John Wheelert arra a kijelentésre, hogy a fizika tárgya alapvetően a Világegyetem fundamentális információtartalmának a feltárása. Ennek ellenére nem várható, hogy a fizikusok elözönlenék a hazai és nemzetközi információtechnológiai pályázatokat. Ugyanis a fenti megállapításoknak a napi haszontermelésnél sokkal izgalmasabb következményei ígérkeznek. G. 't Hooft (6. kép) 1993-ban radikális általánosítását adta Bekenstein észrevételének, amikor a Világegyetem egészét leírni képes, a jövőben megalkotandó elmélet szerkezetére felállította a holografikus elv hipotézist [5], ami azt állítja, hogy a Világegyetem legalapvetőbb független szabadsági fokai kétdimenziós sokaságot alkotnak. Miután óriási tartományról van szó, a határoló felület közelítően síkkal ábrázolható. A tartomány belsejében zajló folyamatok teljes információtartalma ezen a távoli „vetítővásznon” elhelyezkedő szabadsági fokokban rejlő információval meghatározott, és a határ viselkedéséből információvesztés nélkül származtatható. 't Hooft párhuzamba állította ezt az elképzelést a háromdimenziós képek kétdimenziós felületen történő tökéletes kódolásával, a hologrammal. Ennek alapján a fentebb szereplő entrópiakorlátot holografikus felső korlátnak hívják. Ez a korlát kissé csökkenthető, ha feltesszük, hogy a galaxisokba tömörült anyag termikusan tökéletesen szigetelt, azaz a tágulás a mikrohullámú háttérsugárzás lecsatolódása óta adiabatikus. Az akkori, nagyjából ezerszer kisebb tértartomány sugarával számolva a holografikus entrópiakorlát körülbelül milliószorta kisebb a fenti értéknél. A holografikus elv hívei nemcsak egyenlőtlenségként teljesülő felső korlátot, hanem egyenlőséget is remélnek a fenti becslésből kiolvasni. Ez pedig csillagászati „vadászatot” indít a hiányzó entrópia nyomában! Egy 2008 júniusában megjelent cikk P.H. Frampton amerikai fizikus tollából azt javasolja, hogy nemcsak szupermasszív fekete lyukak, hanem például a naptömeg ezerszeresét hordozók után is kutatni kellene gravitációs mikrolencse hatásuk felhasználásával. Elegendő számban az ilyen méretű fekete lyukak jelentősen hozzájárulhatnának a jelenlegi entrópiatartalmat a holografikus felső korláttól elválasztó „szakadék” kitöltéséhez. A történet lezáratlanul vezet a mai részecskefizikai kutatások élvonalába, miután I. Klebanov és L. Susskind, valamint B. Thorn felismerték, hogy a húrelméletnek van olyan megfogalmazása, amely teljes mértékben megfelel 't Hooft várakozásának. Ugyanakkor mindmáig izgalmas vitakérdést jelent, hogy a fundamentális (Planck-hossznyi méretekben releváns) szabadsági fokok számát általában korlátozza-e a holografikus elv. Érdemes megjegyezni, hogy a fekete lyuk felületére koncentrált dinamikai szabadsági fokok feltevésével a fekete lyukak keletkezése és elpárolgása unitér folyamat, azaz a fekete lyukba hulló információ annak felületén tárolódik valamiképpen. Nemrég színpadias gesztussal az információvesztés lehetőségét eredetileg pártoló Hawking vesztesnek nyilvánította magát és átállt a holografikus elvet elfogadók táborába. Zárásként az abszolút fekete test egykori és a fekete lyuk jelenkori tudománytörténeti szerepe közötti párhuzamra hívnám fel a figyelmet. Az abszolút fekete test sugárzásának univerzális jellege lehetővé tette, hogy Plancknak arra talált kvantumos leírását csakhamar más jelenségkörben fellépő „oszcillátorokra” is kiterjesszék, néhány évtized alatt kialakuljon a kvantum- természettudomány. Elképzelhető, hogy hasonló univerzalitású elméleti keretté épül a tetszőleges objektum által hordozott információ, amely keret jelenlegi megértési szintjét a fekete lyukak entrópiájára alapozott entrópiamaximum tulajdonsága, és az abból kinőtt holografikus elv képviseli. Irodalom___________________
Az MTA Fizikai Osztály és az ELFT által Max Planck születésének 150. évfordulójának tiszteletére rendezett emlékülésen elmondott eloadás írott változata.