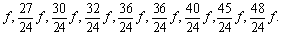
HANGSZEREK A »SEMMIBŐL«

Nagy Anett, Radnóti Miklós Kísérleti Gimnázium, Szeged Papp Katalin, SZTE Kísérleti Fizikai Tanszék, Szeged Öveges tanár úr kísérleteivel egyetemista koromban találkoztam először. Akkor kaptam kedvet az otthoni kísérletezéshez, és azóta keresem azokat a kísérleteket, amelyekhez csak hétköznapi, mindenki számára hozzáférhető eszközök kellenek. A következőkben Öveges tanár úr emléke előtt tisztelegve olyan egyszerű kísérletek leírása található, amelyek segítségével akár kis koncertet is adhatunk. A végkorrekciós tényező meghatározása egy látszólag egyszerű mérés, azonban nagyon jól használható komolyabb összefüggések meghatározására, fizikai és matematikai fogalmak elmélyítésére.

Elméleti háttér

Poharakkal, csövekkel, üvegekkel zenei előképzettség nélkül is bármelyik osztály adhat szórakoztató koncertet. Annyit kell mindösszesen tudnunk, hogy a természetes(dúr) hangskála hangjainak frekvenciái - dótól dó’-ig olyan arányban nőnek, mint a következő számsor: 24, 27, 30, 32, 36, 40, 45, 48. Ez azt jelenti, hogy ha a házi készítésű hangszeren egy teljes oktávnyi hangot szeretnénk megszólaltatni, akkor a kiinduló (alaphanghoz) képest az oktávon belüli többi egész hanghoz tartozó f frekvenciákat a következő törtek segítségével kaphatjuk meg:

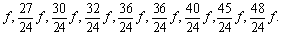
A rezgés során létrejövő legerősebb alaprezgés  hullámhossza a rezgő levegő vagy vízoszlop hosszával arányos [1]. Mivel egy hullám f frekvenciája és λ hullámhossza egymással fordítottan arányos mennyiségek, az előbbiek alapján egy adott l hosszúsághoz tartozó kezdő hanghoz képest a többi hosszat az előbbi törtek reciprokaként kaphatjuk meg(a törteket egyszerűsítettem):

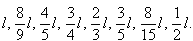
Házi hangszerek
Zene-csövek

A diákok között legnépszerűbb „hangszer” a zene-cső (1. ábra). Megszólaltatása senkinek sem jelenthet gondot, és már elsőre is biztosan sikerül. Vékony műanyag csöveket megfelelő hosszúságúra vágva egy olyan hangszert kaphatunk, amellyel zenélhetünk, ha a tenyerünkhöz ütögetjük a cső egyik száját. A csőben levő levegő ekkor rezgésbe jön és a cső hosszától függően különböző hangokat hallhatunk. A csövek oldalára érdemes ráírni a csőhöz tartozó adott hangot, illetve kisebbek számára érdemes színkódot is használni. Így ezzel a hangszerrel akár egy óvodás csoporttal is zenélhetünk, ha kivetítjük a színekkel kódolt hangsort és rámutatunk a soron következő színre.  

 
A zenecsöveket 20 mm külső és 16 mm-es belső átmérőjű, vízvezeték-szereléshez használt műanyag csövekből készítettem, de más csövek is alkalmasak a „zenélésre”(2. ábra). Ezek viszonylag olcsón beszerezhetők, általában 2 m-es hosszúságban, amelyből egy nyolc hangból álló hangsor kivágható. A 20 mm-es műanyag csőből készített hangsorban a megfelelő hangokhoz tartozó csőhosszakat mutatja az 1. táblázat [2].

 
Néhány egyszerű dallam a gyakorláshoz

A Boci-boci tarka előadásához C-től C’-ig az egész hangokra van szükségünk. A dallam a következő hangokból áll:

 
A Hull a pelyhes fehér hó transzponált dallama a következő:
 

 Pohár-zene

 Tegyünk egymás mellé egyforma üvegpoharakat és töltsük meg különböző magasságig vízzel(3. ábra)! Egyik kezünkkel fogjuk le a poharat a talpánál. Nedves ujjunkat végighúzva a pohár peremén, a pohár fala rezgésbe jön és hang keletkezik. Az ujjunk ugyanis hol megtapad, hol megcsúszik a pohár peremén, ezzel rezgésbe hozva a pohár falát. Minden testhez tartozik egy sajátfrekvencia, amelyen rezeg, ha magára hagyjuk. A poharakba töltött különböző magasságú vízoszlopok különbözőképpen módosítják a pohár sajátfrekvenciáját, így különböző magasságú hangokat hallunk. Egy elektronikus hangolóval, vagy énekkaros diákok segítségével néhány perc alatt összeállítható egy hangsor a poharakból. Egy kis gyakorlással pedig egy-egy dalt is előadhatunk a segítségükkel. A kísérlet alkalmat ad egy kis tudománytörténeti emlékezésre, ugyanis hasonló elven működik az üvegharmonika nevű régi hangszer.

 Benjamin Franklin angliai látogatása során találkozott egy zenésszel, aki vízzel töltött különböző poharakat egymás mellé téve úgy „zenélt”, hogy végighúzta a poharak peremén a nedves ujját. Miután hazatért, 1761-ben készített egy zenélő eszközt, az üvegharmonikát (4. ábra), amely közös tengelyre felfűzött üvegedényekből állt. A hangszert pedállal forgatta, mint a régi varrógépeket, és nedves ujjal szólaltatta meg. A hangszer elkészültekor ezt írta egyik barátjának, a torinói Beccaria professzornak. „Talán némi örömet tudok szerezni önnek, hiszen hazája a zene országa. 32 üveg félgömb felhasználásával új hangszert készítettem. Úgy érzem, valamicskével gazdagítottam ezzel a legbűbájosabb tudományt, a muzsikát, amelynek mindannyian rabjai vagyunk. Hangszerem szava édes a fülnek, egyaránt zeng halkan és erősen, s ha egyszer behangoltuk, megtartja pontosságát. Az ön országának tiszteletére olasz nevet adtam találmányomnak, úgy hívják: armonica.” [3]

Az üvegedényeket nagyság szerint fűzte egymásba és színes festékkel jelölte a különböző hangokat. Azüvegharmonikán nagy nyilvánosság előtt először a bécsi udvarban játszott Mária Terézia és József trónörökös jelenlétében Marianna Davies művésznő, aki ezek után Marie Antoinette francia királynőnek is adott leckéket. A hangszer nagyon népszerűvé vált, ezrével gyártották abban az időben. Az üvegharmonika számos zeneszerzőt is megihletett, például Mozart is komponált egy darabot - Adagio és Rondo KV 617 (5. ábra) - és 1815-ben Beethoven egy melodrámájában a narrátor elbeszélése alá komponált zenét üvegharmonikára.

A korabeli történetírók szerint az üvegharmonikán rendszeresen játszó zenészek egy része arról számolt be, hogy érzelmileg lehangolja őket a hangszer. Úgy gondolták, hogy a hangszerben keltett rezgések az ujjaikon keresztül bejutnak a szervezetükbe és rosszkedvet gerjesztenek. A vizsgálatok inkább ólommérgezéssel magyarázták a zenészek lehangoltságát. A hangszer üveg félgömbjei ólmot is tartalmaztak, így elképzelhető, hogy a hangszerből jutott nagyobb mennyiségű ólom a szervezetükbe. Mivel azonban a 18. században igen elterjedt volt az ólom használata, így az ólom számos más forrásból is bejuthatott a zenészek testébe [4].

Az üvegharmonika azóta is meg-megjelenik a koncerttermekben, ebben az évben is jó néhány hazai koncerten találkozhattak a hangszer különleges hangjával az érdeklődők.

Befőttes üveg mint hangszer

A poharak mellett befőttes üvegekkel is zenélhetünk. Vegyünk 8 darab egyforma befőttes üveget és töltsük meg azokat különböző magasságig vízzel. Valamilyen pálcával, kanállal üssünk rá az üvegekre. Azt vehetjük észre, hogy minél magasabb a vízoszlop az üvegben, annál mélyebb hangot hallunk. A jelenség magyarázata hasonló a pohár-zenében leírtakhoz: ahogy ráütünk az üvegre, abban rezgéseket keltünk, az üveg a sajátfrekvenciájának megfelelően rezgésbe jön. Az üveg fala érintkezik az üvegbe töltött vízoszloppal, így az is rezgésbe jön és módosítja az üveg sajátfrekvenciáját. Ezért hallunk különböző magasságú hangokat különböző magasságig vízzel töltött üvegek megütésekor. A megfelelő hangsor összeállításához a megfelelő vízoszlop-magasságokat kell megkeresnünk, akár hallás útján vagy egy gitárhangoló segítségével.

Hagyományos 1 literes befőttes üvegeknél a következő h magasságokig érdemes tölteni az üvegeket vízzel. Sajnos nagyon különböző befőttesüvegeket találhatunk a boltokban - így érdemes inkább saját üvegeinket hallás útján behangolni -, ezért a természetes skála hangjaihoz rendelhető vízoszlop-magasságok inkább közelítő értékek:
 

 
Hangsor üvegekből

Egy másik egyszerű és olcsó hangszer a műanyag üdítős palack(vagy a sörös üveg, 6. ábra). Fél literes egyforma üdítős üvegekbe különböző magasságú vízoszlopot töltve szintén készíthetünk hangsort. Az üveg szája felett elfújva a levegőt, a palackban levő levegő rezgésbe jön és a vízszintnek megfelelően hangot ad. A palack megszólaltatásához kell egy kis gyakorlás, de ha valaki egyszer megérezte a kézben tartott palack rezgését, utána már nagyon könnyen előidézheti a megfelelő hangot.

Érdemes felhívni a diákok figyelmét arra, hogy míg a poharas kísérletben a magasabb vízoszlop mélyebb hangot eredményezett, addig ebben a kísérletben annak a palacknak lesz mélyebb a hangja, amelyben alacsonyabb a víz szintje. Ennek a látszólagos ellentmondásnak az a magyarázata, hogy a poharak és a befőttes üvegek esetében az üveg fala a vízoszlopot hozza rezgésbe, amikor átfújunk az üveg szája felett, akkor közvetlenül az üvegben található levegőoszlop jön rezgésbe. Minél nagyobb a levegőoszlop magassága - vagyis minél kevesebb víz van az üvegben -, annál mélyebb lesz a megszólaltatott hang.

 A palack nagy előnye a poharakkal szemben, hogy sokkal könnyebb behangolni, törhetetlen, és akár egy egész osztály részt vehet vele egy koncerten(7. ábra). Gitárhangolóval igen gyorsan összeállítható egy hangsor, és ha az üvegeken alkoholos filctollal megjelöljük a vízszintet a későbbiekben nagyon könnyen feltölthető és beállítható. Mivel egy adott hangmagassághoz tartozó vízszint függ a palack paramétereitől, így nem adható meg egy univerzális hangmagasság-vízoszlop táblázat. Ha nem érzünk elég önbizalmat magunkban a palackok behangolásához, kérjünk segítséget zeneileg képzett diákoktól vagy az iskola énektanárától. A vízoszlopszintek meghatározása csak néhány percet vesz igénybe, így nem jelenthet megterhelést annak, akit megkértünk.

 Pille-palackos ütőhangszer

A műanyag csöveket a befőttes üvegekhez hasonlóan is használhatjuk hangszerként. Másfél literes palackokat töltsünk meg különböző magasságokig vízzel és szájuknál fogva kössük fel őket sorban egy hosszú lécre. Kezdjük azzal, amelyikben a legtöbb víz van - ez lesz a legmélyebb hangú - és fejezzük be a legkevesebb vizet tartalmazóval. A hangszer megszólaltatásához üssünk rá valamivel a lécről lelógó palackok oldalára. Az így kapott hangszer a befőttes üveghez képest tompább hangot ad, de nagy előnye, hogy törhetetlen, ha pedig elreped, akkor sem balesetveszélyes. A természetes skála hangjaihoz rendelhető h vízoszlop- magasságok:

Papírhenger-xilofon

Alufólia vagy folpack(esetleg papírtörlő) papírhengeréből egyszerűen készíthetünk xilofont (8. ábra). Vegyünk 8 egyforma papírhengert és vágjunk le a végeikből úgy, hogy a természetes skála hangjaihoz a következő hosszúságú csöveket kapjuk:

Tegyük a hengereket egymástól 2 cm távolságra! Egy zsinór segítségével rögzítsük egymáshoz a hengereket úgy, hogy a zsinórt áthurkoljuk a hengereken. Az így elkészült xilofonon egy műanyag bot segítségével játszhatunk [5].

 
Egy kísérleti feladat üvegcsövekkel

A hang terjedési sebességének és a végkorrekciónak mérése üvegcsövek segítségével  998-ban az OKTV kísérleti fordulójában a diákok a hang terjedési sebességét mérték üvegcső-rezonátor segítségével. Hangforrásként egy telefonkagylót használtak, ami a számítógéppel megvalósított jelgenerátorhoz volt kapcsolva. A számítógépes programban a diákok a hang frekvenciáját és amplitúdóját változtathatták. A hang terjedési sebességének meghatározása után a diákoknak össze kellett hasonlítaniuk a tényleges frekvenciához elméletileg adódó rezonanciahosszat a mért értékekkel, és olyan korrekciós eljárást kellett keresniük, amelynek figyelembevételével a mért adatokból közvetlenül megkapható a terjedési sebesség helyes értéke [6].

Ez a kísérlet nagyon egyszerűen elvégezhető egy üvegedény, különböző átmérőjű üveg- és műanyag csövek segítségével. Az üvegcsövet egyik kezünkkel tartva helyezzük az üvegedénybe. A cső felső szájához helyezzünk egy rezgő hangvillát és az üvegcső mozgatásával keressük meg a rezonancia helyét (9. ábra). A rezonáló levegőoszlop, vagyis a vízből kiemelkedő csőhossz mérésével a hang terjedési sebessége számolható.

 Az üvegcső egyik végén zárt, a másik végén nyitott rezonátorként alkalmazható. Ekkor a levegőoszlop sajátrezgését a csővégekről visszavert hullámok interferenciája alakítja ki, pontosabban arra a frekvenciára rezonál a cső, amelyen ezeknek a hullámoknak a fáziskülönbsége adott helyen állandó. Ahol a cső impedanciája igen nagy(zárt csővég) a nyomáshullám 0 fázisugrással, ahol nulla(nyitott csővég) π fázisugrással verődik vissza, mégpedig 100%-ban. Így a rezonátor energiája állandó maradna, ha a belső veszteségek apránként nem emésztenék fel. Mindez azt is jelenti, hogy csőben rezonáló levegőoszlop rezgéseit kívülről nem lehetne hallani – energia a csőből nem lépne ki. Fülünket a cső nyitott végének közelében tartva azonban meggyőződhetünk arról, hogy ez nincsen így: a cső vízből kiálló részének hosszát változtatgatva, könnyen találunk olyan csőhosszat, amelynél a cső jól hallhatóan zeng(rezonál). Ez azt is jelenti, hogy a cső a nyitott végén sugároz, vagyis a nyitott végen bekövetkező fázisugrás mégsem lehet π. Ekkor azonban a rezonáló levegőoszlop hossza nem lehet pontosan λ/4 páratlan számú többszöröse, hanem kisebb annál, mert a fázisugrás kisebb mint π. Az, hogy a nyitott végen bekövetkező fázisugrás mennyire különbözik π-től, s így a kialakuló állóhullámképnek a nyitott vég fele eső duzzadóhelye menynyivel esne a csövön kívülre, az a nyitott végen bekövetkező impedanciaugrástól, tehát a szabad tér és a cső impedanciájának viszonyától függ: minél nagyobb a cső keresztmetszete, annál kisebb az impedanciája. A kisebb impedanciaugrás kisebb fázisugrást eredményez, így nagyobb csőkeresztmetszetnél nagyobb „kilógás” várható.
Az elméleti esetben - amikor a csőhossz(2k+1)λ/4 alakú - a rezonátorcső hosszának megmérésével a hang terjedési sebessége könnyen meghatározható:

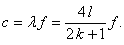
Ha l helyett(az állóhullámkép hossza a duzzadóhelytől  csomópontig) kisebb értékkel számolunk(a rezonátorcső hosszával) a sebességre a ténylegesnél kisebb értéket kapunk. A 2. táblázat a különböző átmérőjű csövekkel végzett méréseink eredményeit tartalmazza.
A 2. táblázat adataiból jól látható, hogy egy adott átmérőjű üvegcső esetén a frekvencia növelésével a rezonáló levegőoszlop hossza, így a hullámhossz csökken, mivel a frekvencia és a hullámhossz között fordított arányosság van, ha a terjedési sebesség állandó. Mivel a kísérlet közben a hőmérséklet közel állandónak tekinthető, és a levegő összetételét sem változtattuk meg, a terjedési sebességet állandónak tételezhetjük fel. Ha az adott átmérőjű csőnél a különböző frekvenciák esetén kapott levegő-oszlophosszakból terjedési sebességet számolunk, a kapott sebességértékek a valóságosnál kisebbnek adódnak. Ezt az eltérést nagyobb átmérőjű csöveknél nagyobbnak találtuk. A 3. táblázatban a különböző átmérőjű üvegcsövekkel végzett kísérleteink eredményeit foglaltuk össze. Ha a csőhosszakat a frekvenciaértékek reciprokainak függvényében ábrázoljuk, olyan lineáris függvényeket kapunk, melyek nem az origóban metszik a függőleges tengelyt, hanem attól -b méterre. A legkisebb és a legnagyobb átmérőjű csövekkel végzett kísérletekhez tartozó grafikonok a 10. és 11. ábrán láthatók.  

3. táblázat

A különböző átmérőjű csövek esetében kapott egyenesek meredekségeiből számolt c terjedési sebességeket és a b/d végkorrekciókat a 3. táblázatban foglaltuk össze. Az adatokból látható, hogy a kapott értékekre illesztett egyenesek meredekségéből számított terjedési sebességek átlaga igen jól megközelíti a hang terjedési sebességének elfogadott értékét. A táblázat utolsó oszlopában a számolt végkorrekciós értékeket tüntettük fel. A kapott értékek jól megközelítik a szakirodalomban elfogadott 0,3-0,4 közötti értéket. A végkorrekció az átmérő növekedésével - kísérleti eredményeink alapján - enyhe monoton csökkenést mutat (12. ábra).

Van azonban más lehetőség is a korrekciós tényező meghatározására. Ha a rezonáló levegőoszlop hosszát egy adott frekvencián a csövek belső átmérőinek függvényében ábrázoljuk, akkor egy olyan süllyedő egyenest kapunk, amelynek meredeksége a korrekciós tényező értékével egyezik meg, és az adott frekvenciához tartozó, elméletileg megállapított effektív hossznál metszi a tengelyt. Mivel l_eff = l+xd, ezért:

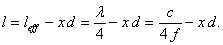
A különböző frekvenciákon mért rezonanciahosszakat  a belső átmérő függvényében ábrázoltuk, a grafikonok a meredekségeit(a korrekciós tényezők -1-szeresét) és a tengelymetszetekből számolt terjedési sebességeket a 4. táblázatban gyűjtöttük össze. Az eredmények nagyon jól megközelítik azokat az értékeket, amelyeket az adott belső átmérők esetében a rezonanciahossznak a frekvencia reciprokától való függésének vizsgálatakor kaptunk (2. táblázat ).

 
A kísérletet különböző átmérőjű műanyag csövekkel is elvégeztük. A mérési eredményeket, az 5. táblázat tartalmazza. (A rezonanciahosszakat a frekvencia reciprokainak függvényében ábrázoltuk.) Érdekes, hogy műanyag csövek esetében a korrekciós tényező értéke nagyobb volt, míg a terjedési sebesség értéke kisebbnek adódott. Az üveg- és műanyag csövekkel elvégzett kísérletek eredményeinek különbözősége azonban nem meglepő, hiszen ezen anyagok rugalmassági tulajdonságai eltérnek egymástól.

A rezonanciahely közvetlen közelében - a csőhosszat igen finoman növelve - feltűnő, hogy maximális intenzitást bevezető viszonylag gyors erősödést egy igen gyorsan bekövetkező elhalkulás követi, amelyben az észlelhető intenzitás jóval a rezonanciától távoli helyzet intenzitása alá esik, majd csak ezt követően áll vissza arra az értékre, ami a rezonanciától mentes helyzetekre jellemző. Ennek magyarázata abban rejlik, hogy amikor a csőben uralkodó intenzitásviszonyokra a csövön kívüli észlelésből következtetünk, lényegében nem azt vizsgáljuk, amire kíváncsiak vagyunk. A csövön kívül észlelt intenzitás nemcsak attól függ, hogy magában a csőben milyen intenzitásviszonyok uralkodnak, hanem, hogy a belépő és kilépő hullám milyen fázisban találkozik.

A rezonanciahelyet átlépve a rezonátor fázisa π-t ugrik, így ha a kilépő hullám korábban erősítést adott a belépővel, akkor a váltás után nem meglepő a gyengítés. Mindez azt is jelenti, hogy a kívül észlelt intenzitásmaximum nem szükségképpen esik egybe a belül tapasztalt amplitúdómaximummal, ez a maximum és a minimum hely közé esik. Ezek alapján rezonanciahelyzeten azt értjük, amikor az amplitúdó a csövön belül a legnagyobb, vagyis amikor a cső szájánál kifelé haladó hullám visszaverődés után pontosan azonos fázisban találkozik a cső szájánál éppen belépő külső hullámmal. Az előbbiek alapján ez a helyzet a csövön kívül intenzitásészlelés alapján pontosan meg sem kereshető, de az egymáshoz közel eső minimum- és maximumhelyek együttes figyelembevételével kisebb hibával határozható meg, mint csupán a maximumok megfigyelésével.

 A hang terjedési sebességének és a hőmérsékletnek, illetve a közeg anyagi minőségének a kapcsolata

A hang terjedési sebességét, így a rezonáló levegőoszlop hosszát befolyásolja a levegő hőmérséklete. Kísérletileg ezt a jelenséget is vizsgálhatjuk az előbbi egyszerű kísérleti elrendezéssel. Tegyünk egy vízen úszó gyertyát a víz felszínére, és az üvegcsövet helyezzük úgy a vízbe, hogy a gyertya a csövön belül legyen. Ha egy hangvillával megkeressük a rezonancia helyét, akkor - leolvasva a rezonáló cső hosszát - megkaphatjuk a hang terjedési sebességét a megemelkedett hőmérsékleten. A kísérletet 440 Hz-es hangvillával és 4 cm-es belső átmérőjű csővel elvégezve a rezonáló levegőoszlop hosszára 18,9 cm helyett 19,6 cm-t kaptunk, amiből terjedési sebességre korrekció nélkül 345 m/s-ot, korrekcióval 350 m/s-ot kapunk.
A kísérlet arra is jól használható, hogy egyszerű eszközökkel demonstráljuk: a hang terjedési sebessége különböző gázokban különböző. Ha egy pezsgőtablettát dobunk a vízzel teli tárolóedénybe, és biztosítjuk, hogy a pezsgőtabletta mindvégig a vízben úszva a csőben maradjon, akkor a felette levő levegőoszlopban széndioxid molekulák is lesznek. Ezáltal megváltozik a hang terjedési sebessége. Ezt a kísérletet 3 cm-es belső átmérőjű üvegcsővel és 440 Hz frekvenciájú hangvillával végeztük el. Egy metronóm hangjára figyelve a pezsgőtabletta vízbe dobásától kezdődően 10 másodpercenként megmértük a rezonáló levegőoszlop hosszát.
Ha a rezonáló gázoszlop hosszát, illetve az ebből számolt terjedési sebességet az eltelt idő függvényében ábrázoljuk (13. és 14. ábra), látható, hogy a pezsgőtabletta oldódásával a rezonanciahossz megváltozik.
A 13. ábrán jól látszik, hogy a pezsgőtabletta oldódása során egyre csökkent a rezonáló gázoszlop hossza, amely a bedobástól számítva a 80. másodperc körül volt a legkisebb. Ekkor lehetett a szén-dioxid mennyisége a legnagyobb a csőben található levegőoszlopban. Ezután a gázoszlop hossza ismét nőtt, míg a 7. perc végére az eredeti rezonanciahosszat mértük. A kapott terjedési sebességek legkisebb értéke 294 m/s, ami a szén-dioxid megnövekedett mennyiségének hatásával magyarázható (14. ábra). Ezzel az egyszerű kísérlettel tehát jól demonstrálható, hogy a hang terjedési sebessége függ annak a közegnek az összetételétől, amelyben terjed.

Összefoglalás

 2008 tavaszán osztályommal felléptünk a gimnáziumunkban a Tavaszi Kulturális Fesztiválon, ahol üvegekkel, poharakkal és csövekkel adtuk elő a Tavaszi szél vizet áraszt című népdalt különböző „hangszereken” (15. ábra). A nagy „sikerre” való tekintettel házi hangszereinkkel(és egy másik osztállyal) az Arany János Tehetséggondozó Program szegedi konferenciáját nyitottuk meg.

Kísérletezni mindig élmény, tanárnak, diáknak egyaránt. A hétköznapi eszközök nagy előnye, hogy a kísérleteket otthon is megismételhetjük, továbbfejleszthetjük.

Az előbbi kísérletek további nagy előnye, hogy miközben a fizikával foglalkozunk, csapatot is építünk és jól is szórakozunk. Ezért mindenkinek jó szívvel ajánlom, hogy próbálják ki ezeket a hangszereket a „semmiből”.

 Irodalom

1. Öveges J.: Az élő fizika. Aranyhal Könyvkiadó, Budapest, 1999.
2. http://www.stevespanglerscience.com/product/1185
3. http://www.pbs.org/benfranklin/l3_inquiring_glass.html
4. http://www.sk-szeged.hu/statikus_html/kiallitas/franklin/talalmany.html
5. Tit T.: Tom Tit második száz kísérlete és produkcziója. Atheneum, Budapest, 1904.
6. Gecső E.(szerk.): Országos Középiskolai Tanulmányi Verseny fizikából, 1994-1998. OKSZ, Budapest, 1999, 43-49.