Fizikai Szemle honlap |
Tartalomjegyzék |
Varga Péter Műszaki Fizikai és Anyagtudományi Kutatóintézet
Felvetik a kérdést: mi a fény, hullám vagy részecske? Nem ilyen gyakran, de az is felmerül, hogy mi az elektron, a proton stb. Az alábbiakban kísérletekről lesz szó, amelyekben ezt szerették volna tisztázni. A cikk végén arra a következtetésre jutok, hogy a fény hullám és részecske. Erről szeretném az Olvasót is meggyőzni.A szerző részben résztvevője, részben közeli szemlélője volt annak a munkának, amelyet később Jánossy-kísérleteknek neveztek el. Innen elindulva ismertetem az ezeket követő, részben az eredeti kísérletek által inspirált további munkákat. Minden munka az interferencia jelensége, illetve annak általánosítása, a fényhullámok korrelációja kérdéséhez kapcsolódik. Eljutunk odáig, hogy kijelenthetjük, létezik olyan interferenciajelenség, amelyet a klasszikus fizika tévesen írle, a kvantumelmélet azonban helyesen. Bár Jánossy a sugárzás kvantumelméletét nem tette magáévá, egy dologban feltétlenül igaza volt: az ortodox felfogást még három évtizeddel a kvantumelmélet felfedezése után is csak gyengén támasztották alá olyan kísérletek, amelyek kétségkívül bizonyították volna azoknak az "ellentmondásoknak" fennállását, amelyekhez az elmélet vezetett. (Az idézőjel használatát a cikk utolsó fejezetében szeretném indokolni.)
A részletes tárgyaláshoz szükséges matematikai apparátust nem ismertetem. Ahol ez hosszadalmas lenne, inkább csak a példákon keresztül mutatom be az eljárást, és csak utalok a matematikai háttérre. A kvantumelektrodinamika apparátusából éppen csak annyit használok fel, amennyi egy fontos kísérlet eredményének igazolásához kell.
Jánossy Lajos (1912-78) 1950-ben jött Magyarországra, mikorra már nevet szerzett a kozmikus sugárzás kutatásában. A harmincas évekre ez a diszciplína már túlnőtt a jelenség külső tulajdonságainak a megfigyelésén. Már megállapították, hogy honnan ered (a világűrből), mi befolyásolja (a Nap és a Föld mágneses tere, a Föld atmoszférája stb.). A hőskor után a kozmikus sugárzás összetételét vizsgálták és felfedezték azt is, hogy az ismert elemi részecskéken kívül továbbiak is léteznek: a pozitron (ma már az orvosi gyakorlatban is használjuk) vagy a két középnehéz részecske, a µ- és a π-mezon (müon, pion). Jánossy továbbment, mérésekkel bizonyította, hogy van a kozmikus sugárzásnak egy nagy energiájú magaktív komponense is [1-3]. A későbbi kutatások során kiderült, hogy ebben a komponensben a pionnál nehezebb, de a nukleonoknál könnyebb részecskék vannak, sőt a nukleonoknál nehezebb hiperonok is. Ez az út vezetett a mai részecskefizikához, amelynek kísérleti eszközei immár a nagyenergiájú gyorsítók.
Jánossy nemcsak kísérleteivel szerzett nevet. Ő írta a kozmikus sugárzás első monográfiáját [4], ez a híres oxfordi Clarendon Press International Series of Monographs on Physics sorozatában jelent meg. A sorozat szerkesztői közé tartoztak Mott és Kapica, szerzői közé Dirac és Heitler. Nem sokkal hazatérése után Jánossy nagy vitával követett előadást tartott az Eötvös Loránd Fizikai Társulatban, amelyet publikált is [5]. Az előadásban és a cikkben fő célja a kauzalitás megvédése volt, rá kívánt mutatni a kvantumelmélet ellentmondásosságára. Felvetette a fundamentális kérdést: "Számos kísérlet van, amely külön-külön a napnál világosabban bizonyítja az elektronoknak, a fotonoknak és a többi elemi részecskének vagy a hullám, vagy a r észecske természetét. Nehézségek akkor keletkeznek, amikor egyszerre akarjuk ezeket az eredményeket magyarázni. Létezik olyan nézet, amely szerint, nem szabad egyszerre tekinteni ezeket a kísérleteket: - azt állítják, hogy a kétféle szemlélet összekeverése nem vezet ésszerű eredményhez. Véleményünk szerint igaz, hogy paradoxonokhoz jutunk, ha a hullám és a részecske természetet szimultán vesszük tekintetbe - de ezek a paradoxonok nem kerülhetők meg az által, ha kikötjük, hogy nem gondolkodhatunk felőlük." [5]
Jánossy analízisét nem ismételjük meg, a részletek az idézett cikkben megtalálhatók. A kísérletek szempontjából felvetett kérdés a következő volt: mi történik, ha egymástól független fotonokkal végzünk kísérleteket? Essen be egy Michelson-interferométerbe (1. ábra) nagyon kis intenzitású fénynyaláb. "Jó okunk van feltételezni, hogy az (....) interferenciakép az egyedi és egymástól független fotonok kontribúciójával jön létre. Minden foton, bár egyetlen pontban nyelődik el, magával hordja - mint tendenciát - az egész interferenciaképet. Minden foton önmagával interferál és elsősorban ott nyelődik el, ahol az interferenciakép nagy intenzitást ad." [5] A gondolat nem új, Dirac [6] még erősebben fogalmazott: "Each photon then interferes only with itself. Interference between two photons never occurs." ("Minden foton önmagával interferálódik. Két foton között soha nincs interferencia." Kiemelés tőlem, V.P.)
Vizsgáljuk tovább a Michelson-interferométert. Az F fényforrásból (1. ábra) kilépő monokromatikus sugár (a monokromátort most nem jelöljük) a T0 részben áteresztő tükörre, innen a T1, illetve a T2 tükrökre, majd visszaverődve újra a T0 tükörsegítségével az M megfigyelési pontba jut. Interferenciát tapasztalunk, vagyis azt, hogy a megfigyelési pontban mérhető intenzitás függ a fénynek a T0 és a T1, illetve a T0 és a T2 közötti utak hosszának különbségétől. Bármely tükör elmozdítása az intenzitás változását okozza, ebből arra következtetünk, hogy a fény mindkét tükörrel kölcsönhatásba lépett. Mindez a fény hullámtermészetét igazolja. A fény frekvenciája igen magas, 500 nm hullámhossz esetében a frekvencia 6 · 1014 Hz, a periódusidő ennek reciproka. Az intenzitás egy perióduson belül még a fázistól is függ, tehát még kisebb az időkülönbség, másképpen: az egyidejűség legalább 10-17 másodperc pontossággal fennáll!
Vegyünk egy másik berendezést (2. ábra). A fényforrás és a részben áteresztő tükör maradjon meg, csak a két másik tükörhelyére tegyünk két D1 és D2 eszközt, és mindkét eszköz külön-külön legyen alkalmas arra, hogy egy beeső foton hatására mérhető jelet bocsásson ki. Ha a fény az előző kísérletben mindkét tükörrel kölcsönhatásba lépett, akkor most egyidejűleg mindkét detektorral is ezt teszi, a két detektor egyidejű jelét a K koincidenciaberendezéssel regisztrálnunk kellene. Ha a kísérlet eredménye negatív, akkor a kauzalitás problémájába ütközünk. Ugyanis, ha a fény mindkét tükröt (1. ábra) eléri, akkor eléri a két elektronsokszorozót is (2. ábra). Ha az egyik jelez és a másik nem, akkora jelző sokszorozónak befolyásolnia kell a nem-megszólalót. A fotoeffektus viszont gyors jelenség, a jelzésnek azonnal, a fény sebességénél nagyobb sebességgel kell elérni a passzív sokszorozót, tehát ellentmondásba kerülünk a kauzalitással.
A két kísérlet végeredményét a kvantumelmélet egyértelműen megjósolta: interferencia lép fel, koincidenciák nincsenek. Viszont az ilyen sarkalatos kijelentés kísérleti ellenőrzést kíván. Már a 20. század elején végeztek az interferenciára vonatkozó kísérleteket, de ezeket a technika haladásával ismételten el kell végezni még akkor is, ha meg vagyunk győződve arról, hogy csupán a meglévő tapasztalatokat erősítjük meg. Erre vállalkoztak Jánossy és munkatársai a 20. század közepén, a korszínvonalának megfelelő eszközökkel. Majd mások, egyre korszerűbb eszközökkel, újra meg újra megtették.
Ha a Jánossy-kísérletek egyes résztvevői (és szemlélői) között fel is merült az a remény, hogy az eredmények talán majd ellentmondanak az elméletnek, egyben közös volt a vélemény: kísérletezni kell.
Nem tartozik közvetlenül a vizsgált témához, de Jánossy fizikusi tevékenységének része egy fontos epizód. Bár nem vette figyelembe a kvantum-elektrodinamika eredményeit, de - mint a kozmikus sugárzás kutatója - mégis hozzájárult azok igazolásához. Ugyanis a kozmikus sugárzás lágy komponensének (az 1-100 MeV energiájú elektronok, pozitronok, γ-fotonok) abszorpciója érdekes jelenséghez vezetett. Egyetlen ilyen energiájú részecske az atomhéj elektronjaival való kölcsönhatása során egyszerre két részecskét kelt: a) a nagy energiájú elektron egy γ-fotont, plusz egy másik elektront, b) a nagy energiájú γ-részecske a Compton-effektus során egy másik fotont és egy elektront, vagy egy elektron-pozitron párt. Ha a másodlagos részecskék energiája még mindig elég nagy, akkor ezek újabbakat keltenek, és így tovább, a részecskék zápora alakul ki, amit úgy észlelhetünk, ha figyeljük, mikorszólal meg egyszerre több Geiger-Müller-számlálócső. Ezek a számlálócsövek egy háromszög vagy ötszög csúcsaiban az alakzatra merőleges irányban helyezkednek el, ekkor legalább két, illetve három részecske kell a megszólaltatásukhoz. Minél több részecske vesz részt a záporban, annál nagyobb a valószínűsége, hogy egyszerre jeleznek a számlálócsövek. Foglaljanak helyet a számlálócsövek egy ólomabszorbens alatt és növeljük az abszorbens vastagságát 0 és 20 cm között. Azt találjuk, hogy a vastagságot növelve a záporok száma növekszik, hiszen egyre több részecske keletkezik, de egy vastagság elérése után a záporok száma csökkenni kezd, mert a részecskék energiája degradálódik, egyre kisebb valószínűséggel keltenek egynél több detektálható részecskét. A jelenség elméletileg is kezelhető, mert az elemi folyamatok hatáskeresztmetszete a kvantumelmélet segítségével kiszámítható, és a kaszkádok követhetők. Ha a záporok számát az abszorbens vastagsága függvényében ábrázoljuk, akkor az elmélet azt mutatja, hogy a görbének egyetlen maximuma van. Bizonyos kutatók viszont azt találták, hogy még egy maximum is fellép, sőt egyesek már harmadik maximumról is hírt adtak. Ha ez így van, akkor vagy a jelenséget leíró kvantumelmélet hibás, vagy a γ-foton mellett létezik még egy semleges részecske, amelynek kölcsönhatása az abszorbens anyagával ugyancsak elektromágneses természetet mutat. Jánossy cikkeiből kiderül [7-9], hogy az újabb maximumnak vélt értékek statisztikusan nem szignifikánsak. (Jellemző, hogy majdnem minden szerző más vastagságnál találta meg a saját második maximumát.) Ezen kívül megtalálta a hibát abban a kísérletben, amelyben a második maximum pregnáns volt, vagy a kísérletet gondosan megismételve nem talált további maximumot.
A speciális relativitáselmélet szerint minden mező legfeljebb vákuumbeli fénysebességgel terjedhet. Jánossy felhívja a figyelmet, hogy mára fotoeffektus létrejöttéhez - a kilépési munka legyőzéséhez is - a fény energiájának gyors kontrakciója szükséges. Ugyanis, ha az Q pontból (3. ábra) kilépő gömbhullám eléri azt az A pontot, ahol elnyelődik, akkora hullám azon részének, amely az A ponttal ellentétes irányba, a B pontba jutott el, a fényénél nagyobb sebességgel kell elérnie az A pontot. Ez igaz akkor is, ha a laboratóriumi fényforrásról vagy egy távoli csillagról van szó. Ezt a vélt vagy valódi jelenséget a foton kollapszusának nevezték el. (Ez a probléma vezette oda Jánossyt, hogy az einsteini speciális relativitáselmélet helyett olyan elméletet írjon fel, ami egyezik a tapasztalattal, de nem követeli meg, hogy elvessük a fénysebességnél nagyobb sebesség létezését.) Azt, hogy a fotoeffektus valóban gyors jelenség, a Mégsem volt jó a koincidenciamérés? című, majd a cikk második részében ismertetendő kísérletünk is igazolja.
A továbbiakban ismertetett két kísérlet az előzőekben felvetett két kérdésre kívánt választ adni:
A kísérleteket a lehető legkisebb fényintenzitás mellett kell elvégezni, hogy kizárjuk azt a lehetőséget, hogy a jelenségek két vagy több foton egyidejű kölcsönhatása miatt jöttek létre.
A belga Cosyns professzor - Jánossynak tett szóbeli közlése alapján - elvégezte a koincidenciakísérletet és negatív eredményre jutott, de nem publikálta [5]. A tűsugárzásnak J. J. Thomson 1907-ben felvetett hipotézise (amelyet Selényi Pál 1911-ben már megcáfolt) kapcsán felmerült, hogy kis fotonszám esetén fellép-e interferencia. Ugyanis, ha a fotonok gömbszerű, lokalizált részecskék, akkor interferencia csak több foton egyidejű kölcsönhatása révén jöhet létre, ezért kis intenzitásnál csökken két vagy több foton találkozásának valószínűsége. Kis intenzitású interferencia megfigyelésével több kísérletet végeztek a 20. század elején, a detektormindig fotografikus lemez volt.1 Taylor 1909-ben azt vizsgálta, hogy fellép-e diffrakció kis intenzitásoknál. (A diffrakciós kép is hullámok interferenciájából áll elő.) A válasz pozitív volt. Dempster és Batho 1927-ben 15 lépcsőből álló rácson, illetve vékony rétegen keletkező interferenciaképből állapította meg az intenzitásfüggetlenséget. A rácsos kísérletekben a legkisebb intenzitás 95 foton/s volt, az expozíció 24 óráig tartott. A kísérletek közös jellemzője, hogy az interferáló hullámok közötti úthosszkülönbség a rácsos kísérletben 0,1-0,2 mm volt, a diffrakciós kísérletekben pedig csak néhány hullámhossznyi.
Kívánatos volt a kísérletet az intenzitáseloszlás fotoelektromos detektálásával elvégezni. Ha az interferométer után az M mérési pontban (1. ábra) elektronsokszorozót helyezünk el, akkor ez minden egyes fotoelektron hatására egy elektromos feszültségimpulzust ad, és módunk van ezeket az impulzusokat megszámlálni. Várhatóan több impulzust számlálunk meg ott, ahol az interferenciacsíkban maximális az intenzitás, kevesebbet, elvben egyet sem, ahol minimális, és így az interferenciakép intenzitáseloszlása letapogatható. Egyetlen mérésben a fény mindkét tulajdonsága megjelenik; a hullám az interferencia létrejöttével, a részecske pedig a fotonszámlálással.
Jánossy aspiránsát, Ádám Andrást bízta meg a kísérlet végrehajtásával. Előbb azt a berendezést kellett elkészítenie (D1 és D2, lásd a 2. ábrát), amelyekkel fotonokat lehet számlálni. Az alap egy USA-beli fotoelektron- sokszorozó volt, ez egyetlen primér fotoelektronból körülbelül százezer elektront produkált, amitől az anódon mintegy 10-9 másodpercig tartó lavina jelent meg. Mivel ebben az időben még nem tudtunk ilyen rövid impulzusokat kezelni, a jelet megnyújtottuk, a kiinduló jel amplitúdója átlagosan 1,6 mV, hossza pedig 1 µs volt. Ezt az impulzust erősítettük, majd megszámláltuk. (Faragó Péter, aki Bay Zoltán munkatársa volt az Egyesült Izzó kutatólaboratóriumában, a [11] publikációhoz csatolta megemlékezéseit. Bay már1938-ban javasolta az elektronsokszorozót az elemi részecskék számlálására, de az eszköz befejezéséig a háború miatt nem jutottak el.)
A kis elektromos impulzusok megszámlálását nehezítette, hogy egy fizikai intézet maga is elektromos zavarok forrása, a szomszéd szobában megszólaló GM-cső jelzéseit a mi berendezésünk is regisztrálta. Ezért leköltöztünk a kozmikus sugárzás vizsgálatára épített föld alatti laboratóriumba, itt a távolság és a vastag földréteg megvédett a zajoktól és a mérőhelyiséget egyetlen kattintással el lehetett sötétíteni. A laboratórium harminc évre az optikai mérések színhelye lett, egy másik jó tulajdonságát, a rezgésmentességet a következő mérésekben ki is használtuk.
A külső zajforrások mellett egy másik, belső zajforrás is fellépett. Detektorunk fotokatódjának kilépési munkája éppen azért, hogy a látható fényt is detektálhassuk, alacsony volt. A fém fotokatód szabad elektronjai egy részének kinetikus energiája már szobahőmérsékleten is nagyobb volt, mint a kilépési munka, ezért a katód viszonylag sok elektront emittált (sötétáram). Detektorunk ezeket éppen úgy megsokszorozta, mint a fotoelektronokat. A sötétáram csökkentésére a detektort cseppfolyós levegővel kellett huteni, de ekkor - a rácsapódó pára miatt - a sokszorozóra kapcsolt 1000 V feszültség átütött. Az irodalom alapján a sokszorozót vákuumba kellett helyezni, viszont ekkor nagyon lassan hult le, a hőt csak a Dewar-edény fala és a sokszorozó ezzel érintkező külső szerelvénye vezette el. Kolumbusz tojása: a sokszorozót tartalmazó csőből előbb eltávolítottuk a szoba levegőjét, majd az egészet száraz levegővel töltöttük fel, és hat óra helyett fél órára csökkent a lehűtés ideje. A detektor teljes szerelvénye a 4. ábrán látható. A sötétáram kicsi volt, 1-2 beütés/s, ezért az általunk használt intenzitás mellett (300 beütés/s) már nem kellett figyelembe venni. Ezzel készen álltunk fotonok számlálására [12].
Essen be a detektorra másodpercenként (időegységenként) n foton, legyen p annak valószínűsége, hogy a fotont detektáljuk, akkor másodpercenként N = pn impulzust regisztrálunk. Azoknak az eseményeknek a száma, amikor a két sokszorozó egyetlen foton hatására jelez egy másodperc alatt εp2 n, itt ε a kettős megszólalás valószínűsége. A koincidenciák számának meghatározásánál azt is figyelembe kellett venni, hogy koincidenciaberendezésünk felbontóképessége véges. A berendezés akkor is jelez egyidejűséget, ha a két sokszorozó egymástól függetlenül, a felbontóképességnek nevezett θv időn belül szólal meg, ezen események, a véletlen koincidenciák száma időegység alatt

Minthogy egy t pillanatban regisztrált foton átlagban
annyi véletlen koincidenciát ad, ahány foton regisztrálódik
a 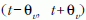 intervallumban,
ez a szám
2θvN-nel egyenlő. Időegység alatt átlagban ennek
N-szeresét kapjuk véletlen koincidenciaként. Így koherens
megvilágítás mellett időegység alatt a koincidenciaszám
intervallumban,
ez a szám
2θvN-nel egyenlő. Időegység alatt átlagban ennek
N-szeresét kapjuk véletlen koincidenciaként. Így koherens
megvilágítás mellett időegység alatt a koincidenciaszám
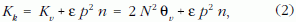
A mérés célja a kettős megszólalás valószínűségének, azaz ε értékének meghatározása volt. Ahhoz, hogy kijelenthessük, hogy igen nagy valószínűséggel léteznek szisztematikus koincidenciák, megköveteltük, hogy
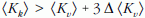
egyenlőtlenség teljesüljön. Itt a csúcsos zárójelpárral a
mérések átlagértékét jelöltük, és  a véletlen
koincidenciák átlagának statisztikus hibája.
a véletlen
koincidenciák átlagának statisztikus hibája.
A véletlen koincidenciák számát úgy kívántuk meghatározni, hogy a két sokszorozót két független F1 és F2 fényforrással világítottuk meg. Mindkettő akkora impulzusszámot produkált, mint az egyetlen koherens F fényforrás mellett külön-külön a két sokszorozó. Mérőberendezésünk sémája az 5. ábrán látható. Mértük a két sokszorozó (N1 és N2) impulzusainak és a K koincidenciák számát.
Világos volt, hogy a mérések a statisztikus adatgyűjtés miatt hosszan eltartanak. Méréseink alapján a sokszorozó hatásfoka, tehát annak a valószínűsége, hogy egy foton hatására egy impulzust kapunk p = 3 · 10-3 volt. Egy sokszorozó másodpercenként körülbelül 400 impulzust adott, tehát a fotonok száma n = 130 000/s volt. Ilyen formán, ha annak valószínűsége, hogy mindkét sokszorozó egyszerre megszólal ε = 1%, akkor 1 percig tartó mérés alatt 0,72 "igazi" koincidenciára számíthattunk. Ugyanekkor, θ = 2,5 · 10-6 s felbontóképesség mellett egy perc alatt Kv = 48 véletlen koincidenciát vártunk, két nagyságrenddel többet, mint az "igazi" koincidenciák száma.
A hosszú mérési idő miatt nem lehetett megkövetelni, hogy berendezésünk stabil maradjon, különösen kritikus volt a θ felbontóképesség állandó volta. Ez áramköri paraméterektől, és az elektroncsövek jellemzőinek öregedésétől függött. A fényforrások intenzitása sem volt állandó. Olyan eljárást kellett találni, amely a lassú változások hatását kiküszöböli. Ezért koherens (egy osztott fénynyaláb) és inkoherens (két független fényforrás) fénnyel végzett méréseket sűrűn váltogatva végeztük, és ehhez illesztettük a kiértékelési eljárást is. A θ felbontóképességet koincidenciamérésből nyert adatokból számítottuk ki, ennél pontosabban nem is lehetett. A felbontóképesség két egymás után következő mérés tartama alatt ugyan nem változott, de az (1) formula alapján kiszámított értéke az intenzitás aktuális értékétől függött
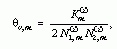
itt a felső index az inkoherens (kétforrásos) megvilágításra, az alsó
indexben a szám a sokszorozóra utal, m a leolvasás sorszáma. Koherens
(egyforrásos) megvilágításnál bevezettünk egy fiktív
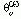 feloldóképességet a következő definíció alapján:
feloldóképességet a következő definíció alapján:
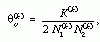
ahol a k felső index a koherens megvilágításra utal. Itt is meghatároztuk a fiktív felbontóképesség aktuális értékét, épp úgy, mint a véletlen koincidenciák esetében. A (2) formula a következőképen módosul
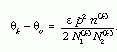
A statisztikus kiértékelés tárgyának a θk,m - θv,m mennyiségeket tekintettük, ebből számítottunk átlagot és hibát. Ha az átlag szignifikánsan eltérne a nullától, akkor létezne valódi koincidencia. Mivel az egyes sokszorozók impulzusszáma a kiértékelésnek ebben a stádiumában állandónak vehető, a kettős megszólalás valószínűsége
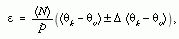
a csúcsos zárójelpár most is az átlagértékre utal.
Három méréssorozatot végeztünk, az elsőt kétperces, a másodikat és a harmadikat századmásodperces váltással. Az eredmény:
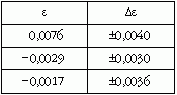
Az egyes sorozatok súlyozott átlaga az
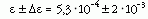
eredményt adta. Tehát annak a valószínűsége, hogy két sokszorozó egyszerre szólaljon meg legfeljebb 3 · 2 · 10-3 = 0,006, hat ezrelék. Ha elfogadjuk, hogy a mérések eredményei Gauss-eloszlást követnek, annak a valószínűsége, hogy fenti állításunk hamis 0,000022.
Jánossy és Náray kísérletei [13-15] három dologban különböztek a 20. század elején végzettektől. Egyrészt a detektor elektronsokszorozó volt, a fotonokat egyenként számlálták meg. Másrészt az előző kísérletekben diffrakciós képet használtak, vagy 16 utas lépcsős rácsot, tehát több hullám interferált. Mindig előnyben részesítjük azokat a kísérleteket, amelyek egyszerűbben prezentálják az eredményt. A legfontosabb különbség az volt, hogy az interferáló hullámok jól szétváltak, és a szétválasztás után nagy utat tettek meg a Michelson-interferométerben a T1 és a T2 tükörig (1. ábra). Ez az út 1-10 cm, de egy sorozatban 14 m volt. Az előző kísérletekben ez az úthossz összemérhető volt a hullámhosszal.
Az első kérdés az volt, mit nevezünk alacsony fotonszámnak. Kétféleképpen járhatunk el. Ha J. J. Thomson nyomán szigorúan pontszerűnek tételezzük fel a fotont, akkor meg kell követelnünk, hogy egyszerre legfeljebb egyetlen foton tartózkodjon az interferométerben. Ha szokványos interferométert tekintjük, a karhossz 10 cm körül van, tehát a fotonszám n << c/10 cm kell, hogy legyen (c a fénysebesség). Ha a fotonhoz hullámvonulatot rendelünk, akkor ennek hossza a kísérleti adatok alapján nem több, mint 1 m, tehát a n << c/1 m egyenlőtlenségnek kell teljesülnie. Ezért az n = 106 foton/s megfelelő választás. Ha össze kívánjuk hasonlítani a kis intenzitásnál kapott interferenciaképet a nagy intenzitású interferenciaképpel, akkor az utóbbira n > 1010 foton/s/nyalábszélesség intenzitást kell választanunk.
A kísérlet megint nehéz technikai feladat elé állította kivitelezőit. Míg a fotonkoincidenciák esetében az "igen vagy nem?" kérdésre kellett választ adni, itt görbéket vettek fel. Interferenciamezőt pásztáztak végig fotonszámláló elektronsokszorozóval, alacsony fotonszám mellett, tehát a megfelelő számú és pontosságú adat eléréséhez hosszú ideig tartó kísérletre kell számítani. Mivel - különösen nagy kartávolságok esetén - az interferenciaképet (a csíkok helyzetét) a környezet rezgései és a hőmérséklet eloszlása is befolyásolják, a mérőberendezés mellett nemcsak nem mozoghatott, de nem is tartózkodhatott ember. (Ilyen volt Joos mérése is, amikor egy 20 m karhosszú interferométerrel megismételte Michelson kísérletét.)
Magát a mérőberendezést a Fizikai Szemléből [14] átvett 6. ábrán láthatjuk. Az interferométer: a párhuzamos B0 nyalábot a Psr rombusz alapú prizma átfogó síkjában levő vékonyréteg tükör osztja ketté B1 és B2 nyalábra. Az M1 és az M2 tükrökön visszavert fény újra az osztótükrön keresztül eljut a T teleszkópba, ez képezi le az interferenciacsíkokat a P elektronsokszorozó előtt elhelyezett S résre. A detektort motor mozgatta programozott pozíciókba. A P detektor impulzusait a megfelelő elektronikus berendezés számlálta, amely lényegében nem különbözött a koincidencia kísérletben használt elektronikától.
Az interferométert szemmel jól érzékelhető nagy fényintenzitás mellett állították úgy be, hogy az interferenciacsíkok függőlegesek legyenek, az S rés ezekkel volt párhuzamos. Az interferenciaképben 3-4 csík jelent meg. Mérték az interferenciamező periodikus csíkjain belül egy-egy pontban az aktuális intenzitást, egyszer kis, egyszer nagy beeső intenzitás mellett. Mivel a B1 és a B2 nyaláb keresztirányú intenzitása nem volt homogén, ezért ezek eloszlását külön-külön is meghatározták minden mérési pontban, végül a sötétáramot is. Mivel a hosszú mérési periódus alatt a fényforrás emissziója is változott, külön monitorozták ezt is. A fontos távolságok az ábrából láthatók.
A fényforrás Hg lámpa volt, amelynek 456,1 nm hullámhosszú vonalát monokromátor szűrte ki. A fény egy része a P* elektronsokszorozóra esett, ez volt a fényintenzitás változásának monitora, jeleit szintén megszámlálták. A monokromátor kilépő rését az L0 lencsével képezték le az interferométer belépő résére. A két rés közötti nagy távolságra azért volt szükség, hogy a lámpa okozta felmelegedést elkerüljék. Kis intenzitás mérése esetén az F1 és az F2 szűrő az ábrán folytonos vonallal jelölt helyzetben volt, tehát már az interferométer bemenetén kicsi volt az intenzitás. Amikor a két szűrő szerepet cserélt (szaggatott vonalak), az interferométer bemenetén nagy lett az intenzitás. Azért kellett az intenzitást az interferométer kimenetén csökkenteni, mert a számláló berendezés véges holtideje miatt nem tudta volna megszámlálni a négy nagyságrenddel megnőtt impulzusszámot. Mindkét szűrő áteresztőképessége közel azonos volt. Az S1 és az S2 takarók a nyalábok intenzitásának mérésére szolgáltak. Mivel tapasztalták, hogy a két nyaláb lokális intenzitáseloszlása megegyezik, csak az egyik nyalábot mérték.
Az interferenciamező minden pontjában hat mérést végeztek. Kis és nagy beeső fényintenzitásnál megmérték az intenzitást az interferenciakép adott pontjában, ugyanezeket külön a B1 nyalábban, végül a sötétáram- impulzusok számát. Egy tipikus mérést a 7. ábrán szemléltetünk. A mért impulzusszámot ? jelöli. ν′ és ν″ a kis, illetve a nagy belépő intenzitásnál az interferenciaképben a detektor helyének a függvényében mért impulzusszám, ν1 a B1 karban, ν0 a sötétáram impulzusszámát ugyancsak, mint a hely függvénye. Az interferenciamezőt többször végigpásztázták, majd átlagolás után az
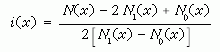
mennyiséget határozták meg külön-külön nagy és kis intenzitásokra. Az indexek értelmezését lásd fent. A 7. ábrán látható az így kiszámított mennyiség. A kis és nagy belépő intenzitások között nincs különbség.
Több méréssorozatot végeztek különböző karhosszak esetén. Így 1-10 cm karhossz mellett végzett 15 mérés az eredmények analízise alapján nem adott szignifikáns különbséget. Ebben a sorozatban a fotonok száma (1,6-2,2) · 106/s volt. 10 cm karhossz mellett a foton 20 cm/(3 · 1010 cm/s) ideig tartózkodott az interferométer egy karjában. Annak a valószínűsége, hogy egyetlen foton van az interferométerben 1,5 · 10-3 volt. Ha a kiterjedés nélküli foton helyett hullámvonulatra gondolunk, amelynek hossza maximum 1 m, a valószínűség akkor is csak ötszörösére növekszik. (Megjegyezzük, hogy a kvantumelmélet szerint a koherens állapotban levő fotonok számát nem ilyen egyszerű meghatározni.)
Megismételték a mérést 14 m karhossz mellett is, 106 foton/s mellett is, ugyanezzel az eredménnyel.
A koincidencia- és az interferenciakísérlet összevetése azt mutatja, hogy a bevezetésben említett ellentmondás valóban fennáll. A fény hol részecskeként viselkedik, lokalizáltan, helyhez (a fotokatódhoz) kötötten hat, hol hullámként viselkedik, az egész interferométert, egy 14 méter hosszú alakzatot is betölt.
Tekintsük át, mit használtunk fel az elméletből. Az interferencia leírásához elegendő, ha az elektromágneses hullámok klasszikus elméletét használjuk fel - egészen a detektorkatódjáig. Implicite azt is feltettük, hogy a detektálás valószínűsége az intenzitás várható értékével arányos. Ez a jelenség kváziklasszikus leírása. A fotoeffektus magyarázatával nem foglalkoztunk, nem volt rá szükségünk. Ez a pragmatikus álláspont - a probléma szőnyeg alá söprése a koincidenciakísérletnél bosszulja meg magát. Itt is elég a klasszikus elmélet egészen a fotokatódokig. Ekkor merül fel a kérdés, miért csak az egyik katódon lép fel az energia kontrakciója?
A kvantum-elektrodinamika szempontjából is kifogást lehet tenni a kísérletek interpretációja ellen. Legyen T az az idő, amennyi alatt a fény eljut a mérőberendezés elejétől a detektorig. Ha fényforrásunk gázkisülés, akkora teljes 4π térszögbe emittál T idő alatt. Ez mindig nagy szám. Viszont maga a mérőberendezés optikája csak igen kis térszöget lát, gyakorlatilag csak 10-2 szteradiánt, tehát egy, a fényforrás által emittált foton legfeljebb 10-3 valószínűséggel van a mérőberendezésben. (Valójában, a veszteségek miatt kisebb, mint 10-3.) Hiába kicsi az a szám, amelyet akkor kapunk, ha a mérőeszközbe belépő teljesítményt elosztjuk a hν energiával, a fotonok száma nagy marad.
Az elvi kifogások dacára folytatása lett a két kísérletnek. Az a tény, hogy egy eredményt más oldalról is alátámasztanak, vagy cáfolni próbálnak az eredmény súlyát növeli, különösen, ha a technika fejlődésével jobban is el lehet végezni a mérést.
1967-ben, jóval a [14, 15] munkák megjelenése után Doncov és Baz tollából cikk jelent meg [16], amelyben cáfolták, hogy kis intenzitásoknál ugyanolyan a normált interferenciakép, mint nagyoknál. Mérőberendezésük lényegesen bonyolultabb volt, minta kritika tárgyává tett Jánossy-Náray-kísérletben esetében, mert Michelson-interferométer helyett Fabry- Perot-interferométert használtak, tehát két interferáló hullám helyett sok, elvben végtelen sok hullám interferenciáját vizsgálták. Nem is fotonszámlálással detektálták az interferenciaképet, hanem fényerősítővel és fényképezéssel. A fényerősítő első része egy nagyméretű fotokatód, erre esik az interferenciakép. A fotokatódot ezután lumineszkáló ernyőre képezik le, most már elektrooptikai úton. A leképezéshez 10-20 kV feszültséget használnak, ezáltal az elektronok energiája megnő és a lumineszcens ernyőn minden egyes fotoelektron észlelhető felvillanást okoz. Ezeket a felvillanásokat fényképezték le. Nagy intenzitások vagy hosszú expozíciós idő mellett a felvillanásokból kirajzolódnának a Fabry-Perot-gyűrűk, a felvillanások olyan suruk lennének, hogy a felvillanások helyei összemosódnának. Kis intenzitásoknál, ha nem túl hosszú az expozíciós idő, az egyes pontok nem fedik egymást, és statisztikai módszerekkel kell megállapítani, vajon periodikusan változik-e a pontok átlagos sűrűsége.
Kis intenzitással végzett mérésnél a szerzők az interferométer elé helyeztek egy abszorbeáló szűrőt. Nagy intenzitás esetén ugyanezt a szurőt a képerősítő elé helyezték át. Így mind a két esetben a képerősítőre már azonos átlagintenzitású fény esett be, a fényképeket össze lehetett hasonlítani. Amíg a Fabry-Perot- interferométerre nagy intenzitású fény esett be, ki lehetett mutatni az interferenciakép létezését, kis intenzitásoknál viszont nem.
A cikk nemcsak a Jánossy-Náray-mérésnek mondott ellent, de az elméleti várakozásnak is. A cikket közlő folyóirat egyik szerkesztőbizottsági tagjától értesültem arról, hogy a főszerkesztő P. L. Kapica is kételkedett a szerzők állításában, de véleménye - helyesen - az volt, hogy az ilyen kísérleti munkát közölni, megvitatni, megismételni, megcáfolni vagy elfogadni kell. Mivel a cikk megjelenésének évében több hónapig Moszkvában dolgoztam, megpróbáltam kapcsolatba lépni a szerzőkkel, de nem sikerült. További közle- ményt a szerzők tollából nem találtam. Ezért felteszem, intézetükben (amelyet nem neveztek meg) találhattak hibát a mérésekben, ezért abbahagyták a kutatást. Ellenkező esetben - tekintettel a téma roppant jelentőségére - folytatták volna, természetesen a szerzők publikációinak özönével.
A jelenség más szerzők érdeklődősét is felkeltette. Reynolds és társa [17] ugyanolyan berendezéssel mértek mint Doncov és Baz. Az utóbbi szerzők fényforrása nagy intenzitást bocsátott ki, ezért már közvetlenül a forrás után is csökkenteniük kellett az intenzitást. (Ez a szurő az egész mérés alatt bent volt.) Reynoldsék a fényforrás kilépő intenzitását eleve kicsire választották. Ugyanis, ha sok az egyidejűleg gerjesztett atom a forrásban (a hullámhosszal összemérhető távolságban vannak az atomok), akkor ezek nem egymástól függetlenül sugároznak. Ők 30 foton/s/detektorfelület mellett, 8 perces expozíciós idő alatt is jól kivehető interferenciagyűrűket kaptak, a gyűrűk egy-egy fotoelektron kilépési helyének megfelelő pontokból állnak (8. ábra).
Grisajev és társai a sugárzó atomok függetlenségét illetően még óvatosabbak voltak [18]. Nem is atomok képezték a fény forrását, hanem egy gyorsító tárológyűrűjében keringő elektronok szinkrotronsugárzása. Mivel a sugárzás spektruma viszonylag széles volt, csak a nulladik rendű interferenciát figyelték meg kétutas (kéthullámos) Jamin-interferométer segítségével. A szerzők becslése szerint a szinkrociklotron tárológyűrűje egy-egy impulzusának lecsengése után az intenzitás olyan szintre csökkent, hogy a detektáló képerősítő katódjára mindössze csak 2500 foton esett be másodpercenként. Azt találták, hogy az interferencia ugyancsak független az intenzitástól. A szerzők a dolgozat végén a [16] cikk egyik szerzőjének mondanak köszönetet, aki éppen az intenzitás intenzitásfüggőségét hirdető cikket írta. Ez alátámasztja feltevésemet, hogy az ominózus kutatást az adott intézetben abbahagyták. Érdekes, hogy Doncov és Baz kísérleteire többször utalnak az irodalomban, mint az őket cáfoló szerzőkre.
Francon és Potocki [19] mutatták meg újra egy kétutas interferométerben, hogy az interferencia intenzitásfüggetlen. A fényforrás egy 20 µm átmérőjű Ne atomsugár volt, amit egy, a sugárra merőleges elektronnyalábbal gerjesztettek. Ezzel kizárták az önfenntartó gázkisülésekben mindig jelenlévő, a termikusnál nagyobb fluktuációkat. A paraméterek megválasztásával azt is kizárták, hogy a sugárzó atomok között kölcsönhatás legyen. A fényforrás a teljes 4π térszögbe 6,3 · 105/s fotont sugárzott ki a használt 585,2 nm hullámhosszon, ezért átlagosan 1500 ns telt el két emisszió között. Ugyanekkor a Ne atom radiációs élettartama az adott átmenetnél 15 ns volt, századrésze az átlagos emissziós gyakoriságnak. Az interferométerben megtett út hossza 45 méter volt, míg az atomi élettartamnak megfelelő úthossz 15 · 10-9 s × 3 · 108 m/s = 4,5 m, tizedrésze az úthossznak.
Mindezek alapján Doncov és Baz [16] méréseit figyelmen kívül hagyhatjuk, és a Jánossy-Náray-méréseket [13-15] igazoltnak tekinthetjük.
_____________________
1 Tonomura és társai [10] elvégezték a fotografikus regisztrálás analóg kísérletét elektronokkal. Lassított filmfelvételt készítettek az interferenciakép kialakulásáról igen kis elektronáram mellett. Az elektronok lumineszcens ernyőre estek, az ernyot kamerával figyelték és időközönként rögzítették a képet. Ahova egy elektron beesett, ott fény villant fel, ezt rögzítette a film. Amíg csak kevés volt a beeső elektronok száma, addig a az egyes lumineszcens felvillanások helye rendezetlennek tűnt, majd észrevehetően sűrűsödni kezdtek a felvillanások ott, ahol az intenzitás nagyobb volt, végül kirajzolódott a periodikus intenzitáseloszlás.