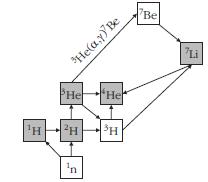
1. ábra. Az Ősrobbanás során lejátszódó magreakciók hálózata. Az írás témáját képező 3He(α,γ)7Be reakció külön jelölve. A stabil izotópok szürke kitöltéssel láthatók
Fizikai Szemle honlap |
Tartalomjegyzék |
Gyürky György
MTA Atommagkutató Intézet, Debrecen
A periódusos rendszer második elemének, a héliumnak két stabil izotópja létezik, a hármas tömegszámú 3He, valamint a négyes tömegszámú 4He, aminek atommagját α-részecske névvel is illetjük. A természetben található hélium szinte kizárólag 4He-ből áll, hozzávetőleg 750 000 4He atomra csak egy 3He jut. A két héliumizotóp magjának fúziós reakciója, a 3He + 4He → 7Be folyamat, vagy a magfizikában megszokott jelöléssel a 3He(α,γ)7Be reakció. Ez a reakció, amelynek során gamma-sugárzás kibocsátása mellett a He magokból 7Be izotóp keletkezik, a mag-asztrofizika két különböző területén is nagy jelentőséggel bír. Ez a két terület az Ősrobbanás után lejátszódó elemszintézis, illetve a fősorozatbeli csillagok hidrogénégése.
 1. ábra. Az Ősrobbanás során lejátszódó magreakciók hálózata. Az írás témáját képező 3He(α,γ)7Be reakció külön jelölve. A stabil izotópok szürke kitöltéssel láthatók |
Világegyetemünk mintegy 13,7 milliárd évvel ezelőtt az Ősrobbanásban keletkezett [1]. A kezdeti, nagy sűrűségű és hőmérsékletű állapotból körülbelül a harmadik perc végére az Univerzum annyira lehűlt, hogy a kvarkokból protonok és neutronok álljanak össze. A hőmérséklet azonban még elegendően magas volt ahhoz, hogy a protonokból és neutronokból magreakciók révén összetett atommagok jöjjenek létre. A részletes számítások azt mutatják, hogy az Ősrobbanás után az 1. ábrán látható reakcióhálózat reakciói játszódhattak le. Az a tény, hogy 5-ös és 8-as tömegszámú stabil atommag nem található, megakadályozta a nehezebb izotópok kialakulását. Újabb néhány perc elteltével a hőmérséklet annyira csökkent, hogy további magreakciók már nem mehettek végbe. A folyamat eredményeképp a megmaradó protonokon (azaz egyes tömegszámú hidrogénmagokon) kívül mindössze négyféle összetett atommag jött létre jelentősebb mennyiségben: a deuteron (kettes tömegszámú hidrogén), a hélium két stabil izotópja, valamint a lítium 7-es tömegszámú izotópja. A szintén keletkező 3H és 7Be radioaktív magok, valamint a megmaradó neutronok rövid időn belül β-bomlás révén rendre stabil 3He, 7Li magokká, illetve protonná alakultak.
Az 1. ábra hálózatában szereplő reakciók sebességének ismeretében kiszámítható az Ősrobbanás során keletkezett izotópok előfordulási gyakorisága, ami összehasonlítható a természetben megfigyelt izotópgyakoriságokkal. Az összehasonlítás eredményét mutatja a 2. ábra. A számítások szabad paramétere az Univerzumunkra jellemző egyik kozmológiai paraméter, a barion-foton arány. A 2. ábra ennek függvényében, sötétszürke sávok formájában mutatja a számított izotópgyakoriságokat. A vízszintes, négyzetrácsosan kitöltött sávok mutatják a csillagászati megfigyelésekből származó gyakoriságokat. A 2001-ben felbocsátott WMAP (Wilkinson Microwave Anisotropy Probe) űrszonda igen nagy pontossággal megmérte a mikrohullámú háttérsugárzás térbeli hőmérséklet-ingadozásait (anizotrópiáját) [2]. Ebből a barion-foton arány precízen meghatározható, a kapott értéket mutatja az ábrán átlósan vonalkázott függőleges sáv. Ennek ismeretében az elemszintézis számításai ellenőrizhetők.
A 4He megfigyelt gyakorisága sajnos igen nagy hibával terhelt, így nem túl meglepő, hogy a számított gyakoriság jól egyezik a megfigyelttel (a 4He görbe a WMAP sávot a megfigyelt gyakoriság sávján belül metszi). Sokkal inkább figyelemre méltó az egyezés a deutérium és a 3He esetén, amelyek gyakorisága nagy pontossággal ismert és a számítások tökéletesen reprodukálják a megfigyelt értékeket az ismert barion-foton arány értéknél. Ez az ősrobbanásos elemszintézis modelljének nagy sikere és egyben az Ősrobbanás fontos bizonyítéka.
Egész más a helyzet a 7Li izotóp esetén, aminek a gyakoriságát - mint az ábrából is látható - mintegy hármas faktorral túlbecsüli az elmélet. A problémára jelenleg nincs általánosan elfogadott magyarázat, az egyik legvalószínűbb lehetőség valamilyen ismeretlen hiba a kezdeti 7Li gyakoriság mérésében. Jelen írás szempontjából azonban egy másik lehetőség az érdekes. A 7Li gyakorisággörbe jellegzetes, határozott minimumot mutató alakja annak köszönhető, hogy alacsony barion-foton arány esetén főként a 3H(α,γ)7Li, míg magas arány esetén a 3He(α,γ)7Be reakció és a 7Be ezt követő β-bomlása vezet 7Li termeléshez. A WMAP kísérlet eredménye szerint ez utóbbi eset áll fenn, tehát a 3He(α,γ)7Be reakció a meghatározó a 7Li termelésben. Az Ősrobbanás utáni percek hőmérsékleti viszonyai esetén a 3He(α,γ)7Be reakció lejátszódási sebességének ismerete természetesen szükséges a 7Li izotóp gyakoriságának kiszámításához. Ez a reakciósebesség a reakció lejátszódási valószínűségéből, azaz hatáskeresztmetszetéből számítható ki. Amennyiben nem ismerjük jól a 3He(α,γ)7Be reakció hatáskeresztmetszetét (ha az például csak harmadannyi lenne, mint hisszük), akkor meg tudnánk magyarázni a 7Li gyakoriságában talált ellentmondást. A kérdéses hatáskeresztmetszet kísérleti meghatározásáról a következő fejezetekben lesz szó, előbb azonban tekintsük át a csillagok hidrogénégési folyamatait, ahol a 3He(α,γ)7Be reakció szintén kulcsszerepet játszik.
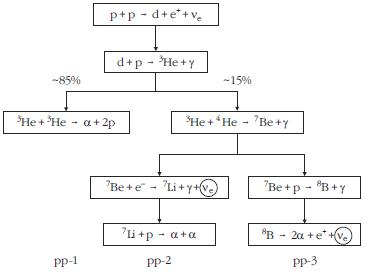
3. ábra. A hidrogénégés pp-láncainak reakciói. A 3He(α,γ)7Be reakcióval induló 2. és 3. lánc felelős a nagyenergiás 7Be és 8B neutrínók kibocsátásáért. |
Napunk - a Világegyetemben található csillagok túlnyomó többségéhez hasonlóan - fősorozatbeli csillag, amelyek közös jellemzője, hogy energiatermelésük hidrogénfúzió segítségével történik, amely során négy protonból egy α-részecske keletkezik [3]. Ez a folyamat nem egy lépésben, hanem több fúziós reakción keresztül, három különböző módon megy végbe, amint ezt a 3. ábra is mutatja.
A három pp-lánc [4] közül leggyakrabban az 1. lánc játszódik le, az azt lezáró 3He+3He → α+2p folyamattal pedig verseng a 3He(α,γ)7Be reakció, ami a Nap esetén mintegy 15%-os valószínűséggel a 2. és 3. lánc irányába tereli a folyamatot. Ez a két ág azért jelentős, mert belőlük származnak a 7Be, illetve 8B béta-bomlása során kibocsátott nagyenergiás neutrínók (az ábrán bekarikázva). Neutrínók legnagyobb számban a legelső p+p → d + e+ + ve reakcióban keletkeznek, ám ezek maximális energiája viszonylag alacsony, mintegy 400 keV (1 eV = 1,6 · 10–19 J). Ezzel szemben a 2. ágban keletkező 7Be neutrínók energiája 384 és 861 keV (monoenergiás neutrínók), míg a 3. ágból a 8B neutrínók folytonos energiaspektruma egészen 16 MeV-ig terjed. A legtöbb földi neutrínódetektor nem érzékeny az 1. lánc alacsonyenergiás neutrínóira, így csak a 2. és 3. (vagy esetenként csak a 3.) lánc neutrínóinak a detektálására van lehetőség [5].
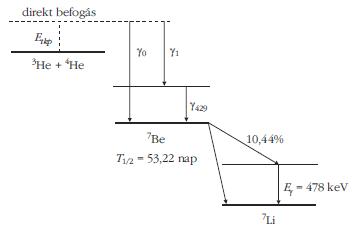
4. ábra. A 3He(α,γ)7Be reakció mechanizmusa. Etkp jelöli a reakcióba lépő magok tömegközépponti rendszerben mért összenergiáját. |
A neutrínódetektálás óriási fejlődésen ment át az elmúlt években, és ez a fejlődés töretlenül halad tovább. Mára már a neutrínók észlelése jelenti a Nap magjában lezajló folyamatok közvetlen vizsgálatának, és így a napmodellek ellenőrzésének egyik legpontosabb módszerét, ugyanis a nagyenergiás neutrínók fluxusa néhány százalékos pontossággal mérhető (illetve hamarosan mérhető lesz). Ugyanakkor a nagyenergiás neutrínófluxus kiszámításához ismernünk kell a versengő 3He+3He → α+2p és 3He(α,γ)7Be reakciók sebességének arányát, amihez a két reakció hatáskeresztmetszetének ismerete szükséges alacsony energián. A két reakció közül a jelen cikk témáját adó 3He(α,γ)7Be reakció hatáskeresztmetszete a kevésbé ismert, ezért jelentős a járuléka a nagyenergiás neutrínók számított fluxusának bizonytalanságához. A továbbiakban e reakció kísérleti vizsgálatának módszereiről, a rendelkezésre álló eredményekről és a reakció vizsgálatának jelenlegi állásáról lesz szó.
A 3He(α,γ)7Be reakció mechanizmusát a 4. ábra szemlélteti. A két héliummag fúziója alacsony (asztrofizikailag jelentős) energián a magfizikában direkt befogás néven ismert folyamaton keresztül zajlik gamma-sugárzás kibocsátása kíséretében, miközben a keletkező 7Be atommag vagy alapállapotban, vagy a 429 keV-es első gerjesztett állapotban jön létre. Utóbbi esetben a 7Be egy újabb gamma-foton kisugárzása révén jut alapállapotba. A 7Be mag radioaktív, 53 napos felezési idővel elektronbefogás révén bomlik 7Li izotóppá. A bomlás során leggyakrabban a 7Li alapállapotban keletkezik, de az esetek mintegy 10%-ában az első gerjesztett állapot jön lére, ami 478 keV-es gamma-sugárzás kibocsátásával jut alapállapotba.
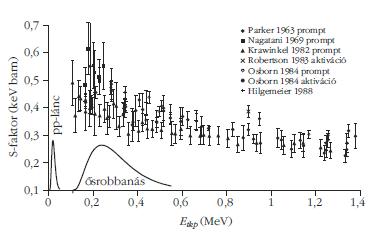
5. ábra. A 3He(α,γ)7Be reakció mért asztrofizikai S-faktora a tömegközépponti energia függvényében (kísérleti eredmények 1988-ig bezárólag). Az ábra bal alsó sarkában a két görbe azt mutatja, hogy a pp-lánc, illetve az Ősrobbanás esetén a reakció milyen energiatartományban játszódik le. A jelmagyarázatban felsorolt kísérletek pontos bibliográfiai adatait lásd például a [6] hivatkozásban. |
A reakciómechanizmus két lehetőséget kínál a hatáskeresztmetszet mérésére. Az első, prompt gamma detektálásos módszerben a direkt befogás során keletkező gamma-sugárzást (az ábra γ1, γ0 és γ429 átmeneteit) kell detektálni a reakció lezajlásával egy időben, tehát amikor egy alkalmas gyorsítóval 3He magokat bombázunk 4He magokkal (vagy fordítva). A másik lehetőség az aktivációs technika, amikor valamilyen módszerrel összegyűjtjük a reakcióban keletkező 7Be magokat, majd a radioaktív 7Be aktivitásának mérésével következtetünk a reakció hatáskeresztmetszetére. Ez legkönnyebben a 7Be bomlások mintegy 10%-át követő 478 keV-es gamma-sugárzás detektálásával lehetséges. A hatáskeresztmetszet meghatározásához ez esetben természetesen tudnunk kell a 7Be izotóp pontos felezési idejét és a 478 keV-es gamma-sugárzás kibocsátási valószínűségét.
A fizikusok már évtizedekkel ezelőtt felismerték a 3He(α,γ)7Be reakció jelentőségét, így mindkét fent vázolt módszerrel számos kísérletet végeztek a reakció- hatáskeresztmetszet meghatározására. Ezek eredményeit foglalja össze az 5. ábra. Az ábra a fúziós reakció tömegközépponti energiájának függvényében mutatja a reakció asztrofizikai S-faktorát, ami a hatáskeresztmetszetből származtatható mennyiség.1
Az ábra bal alsó sarkában a két görbe azt mutatja, hogy a pp-láncra, illetve az Ősrobbanásra jellemző hőmérsékleteken a 3He(α,γ)7Be reakció milyen energiákon játszódik le, azaz mi a reakció lényeges energiatartománya, ahol a hatáskeresztmetszetet ismernünk kell. Mint látható, az Ősrobbanás energiatartományában vannak kísérleti adatok, ám azok szórása igen nagy és a pontok jelentős hibával terheltek. A pp-lánc esetén azonban nincsenek kísérleti adatok, erre az alacsony energiatartományra elméleti modellek segítségével a magasabb energiás mérésekből tudunk extrapolálni. (Az S-faktor alkalmazása miatt a hatáskeresztmetszetek különbsége nem érzékelhető az ábrán. A pp-lánc energiatartományában a hatáskeresztmetszet mintegy 8 nagyságrenddel kisebb, mint a legalacsonyabb energiás kísérleti pontra jellemző érték. Ezért nem lehetséges a kísérleteket a pp-lánc energiatartományában elvégezni.) Az extrapolációt természetesen itt is megnehezíti, hogy a magasabb energiájú pontok jelentősen szórnak és hibájuk is nagy. Ráadásul, ha külön kezeljük a prompt és az aktivációs méréseket, az tapasztaljuk, hogy az aktivációs mérések átlaga mintegy 15%-kal magasabb extrapolált S-faktor értéket eredményez, mint a prompt mérések átlaga. Ez utóbbi probléma felvetette annak a lehetőségét is, hogy a 3He(α,γ)7Be reakció mechanizmusát nem értjük pontosan: lehetséges esetleg 7Be keletkezés prompt gamma-kibocsátás nélkül is.
Mindezen problémák eredményeképpen a Napból származó nagyenergiás neutrínók számított fluxusában messze a legnagyobb magfizikai eredetű bizonytalanság a 3He(α,γ)7Be reakció hatáskeresztmetszetéből adódik, valamint az ősrobbanásos elemszintézis 7Li problémájának megoldásában sem lehet kizárni a 3He(α,γ)7Be reakció szerepét. Természetes tehát, hogy a kísérleti vizsgálatok sora nem állt meg a 80-as évek végén (az 5. ábra eredményeivel), hanem több új mérés eredményei is napvilágot láttak azóta. Az új mérések egyikében a debreceni Atommagkutató Intézet (ATOMKI) nukleáris asztrofizika csoportjának tagjai [7], köztük e cikk szerzője is részt vett, így most e mérés rövid ismertetése következik.
Egy új kísérlet eredményeképp jelentősen javítani kell az 5. ábra által mutatott képen. Ez többféleképpen is elérhető. Célszerű csökkenteni a mért értékek hibáját, a könnyebb extrapoláció érdekében a méréseket a lehető legalacsonyabb energián kell elvégezni, és meg kell vizsgálni a prompt és aktivációs mérések közötti látszólagos ellentmondást. Ez utóbbi úgy érhető el, ha a méréseket mindkét módszerrel, párhuzamosan végezzük, és az eredményeket összehasonlítjuk. Az alábbiakban röviden bemutatott LUNA együttműködés mindhárom cél elérését tervbe vette.
A Nap hidrogénégésében szerepet játszó reakciók általános jellemzője, hogy a magfizikában megszokotthoz képest jóval alacsonyabb energián játszódnak le, ami extrém alacsony hatáskeresztmetszeteket jelent. Emiatt általában nem lehet a magreakciókat laboratóriumi körülmények között a Napra jellemző energiákon tanulmányozni, a magasabb energiákról történő extrapoláció általában elkerülhetetlen. Ez viszont rendszerint annál pontosabb, minél alacsonyabb energián sikerül a méréseket elvégezni. Alacsony energia felé haladva a hatáskeresztmetszet csökkenése miatt egyre nehezebbé válik a reakciók vizsgálata. Kis hatáskeresztmetszetek esetén igen kis intenzitású sugárzás detektálása a feladat, amit a természetes háttérsugárzás jelentősen megnehezít, vagy lehetetlenné tesz. A háttérsugárzás visszaszorításával tehát esély lehet kisebb hatáskeresztmetszetek mérésére, azaz alacsonyabb energiák elérésére is.
A természetes eredetű háttérsugárzás egyik fontos összetevője a kozmikus háttérsugárzás, amit a világűrből érkező nagyenergiájú töltött részecskék, illetve az általuk kiváltott másodlagos, részecske- és gammasugárzás alkotnak. A kozmikus háttérsugárzás csökkentésének egyik módja az, ha a kísérleteket mélyen a föld felszíne alatt végezzük, ugyanis a földkérget alkotó kőzetekben a sugárzás elnyelődik. Az alacsony kozmikus háttér miatt a világ számos pontján működnek föld alatti laboratóriumok, ahol általában olyan ritka eseményeket vizsgálnak, amelyek esetén fontos a minél alacsonyabb háttérsugárzás. Tipikus példája ennek a neutrínó-detektálás, de számos egyéb "ritka esemény" kutatása is föld alatti laboratóriumokban zajlik (példaként említhetnénk a sötét anyag kutatását vagy a kettős béta-bomlás kimutatására tett kísérleteket). Alacsony hatáskeresztmetszetű magreakciók vizsgálata esetén is hasznos lehet egy föld alatti laboratórium, de ehhez részecskegyorsítót kell a föld alá telepíteni.
Jelenleg a világon egyedülállóként a LUNA (Laboratory for Underground Nuclear Astrophysics) olasz-német-magyar együttműködés üzemeltet föld alatti részecskegyorsítót [8]. A gyorsító Olaszországban, Rómától mintegy 100 km-re, az Appenninek hegylánca alatt kialakított LNGS (Laboratori Nazionali de Gran Sasso) föld alatti kutatóintézetben található. A laboratórium fölötti, átlagosan mintegy 1400 méteres sziklaréteg a nehéz töltött részecskéket teljesen elnyeli, míg a neutron- és müonfluxus több nagyságrenddel csökken. Ez utóbbiak az anyaggal való kölcsönhatás során végső soron gamma-sugárzást váltanak ki, tehát a föld alatti laboratóriumban a gamma-háttér is alacsonyabb, ami egy gamma-detektáláson alapuló magfizikai kísérlet (amilyen a 3He(α,γ)7Be reakció vizsgálata) számára előnyös.
A LUNA együttműködés által üzemeltetett berendezés egy mindössze 400 kV maximális feszültségű elektrosztatikus gyorsító. A kis feszültség kis részecskenyaláb- energiát jelent, de az alacsony energián lejátszódó asztrofizikai reakciókhoz általában nincs is szükség nagyobb energiára. A kis hatáskeresztmetszetek miatt azonban nagy nyalábintenzitás szükséges. A LUNA gyorsító esetén az egyszeres töltésű 4He+ ionnyaláb intenzitása 250 µA körüli, ami másodpercenként több mint 1015 bombázó részecskét jelent.

6. ábra. A 400 kV-os LUNA gyorsító fényképe.
A LUNA gyorsító fényképe a 6. ábrán, míg a 3He(α,γ)7Be reakció vizsgálatához használt kísérleti elrendezés sematikus ábrája a 7. ábrán látható. Mivel a tanulmányozni kívánt reakció két nemesgáz-izotóp között játszódik le, gázcéltárgy használata szükséges, ami technikai nehézségeket vet fel. A céltárgygázt (esetünkben a 3He izotópot) nem lehet egy gázcellába zárni, mert technikailag nem lehet olyan vékony fóliával (belépő ablakkal) lezárni a cellát, amin a LUNA gyorsító alacsony energiás nyalábja elnyelődés nélkül képes áthaladni. Így csak ablak nélküli, úgynevezett differenciálisan szívott gázcéltárgy jöhet szóba. Itt a céltárgygázt folyamatosan engedjük be a céltárgykamrába, ami csak egy szűk nyíláson át tud távozni a vákuumszivattyúk irányába. A három egymást követő vákuumszivattyú-fokozattal elérhető, hogy a kamrában stabil legyen a nyomás (esetünkben tipikusan 0,7 mbar), míg a szivattyúk előtt a gyorsító oldalán 10–7 mbar nagyságrendű vákuum tartható fenn.
A hatáskeresztmetszet meghatározásához ismerni kell mind a céltárgyat bombázó 4He magok, mind a 3He céltárgymagok számát. Az első mennyiség meghatározása a nyalábintenzitás mérésével lehetséges, amit általában töltésméréssel oldanak meg, hiszen minden 4He+ ion egy elemi töltésnek megfelelő töltést juttat a céltárgyba. Gázcéltárgy esetén azonban ez nem lehetséges, mert a gázban haladó ionok töltéscsere- reakciókban vesznek részt a gáz atomjaival, így a céltárgykamra végét (ahol a töltést mérni lehetne) már meghatározatlan töltésállapotban érik el, tehát a beeső részecskék számát nem lehet a teljes töltés mérésével meghatározni. Ilyenkor hívható segítségül a kaloriméteres technika, amit méréseinkben mi is alkalmaztunk. Ekkor a töltés mérése helyett a nyaláb által okozott hőteljesítményt mérjük. A kaloriméter működési elve - kissé leegyszerűsítve - a következő: egy fűtőellenállást szabályozó tápegység állandó hőmérsékleten (esetünkben +70 °C-on) tartja a kaloriméter felszínét, ami egyben a gázcéltárgy vége, amibe a nyaláb becsapódik. A kísérlet során a hőmérséklet fenntartásához szükséges teljesítményt mérjük. Amikor a nyaláb bombázza a kalorimétert, a nyaláb okozta melegítés miatt kisebb teljesítménnyel is fenn lehet tartani az állandó hőmérsékletet. A két teljesítmény különbségéből kiszámítható a nyaláb hőteljesítménye, abból pedig a nyalábenergia ismeretében az intenzitása.
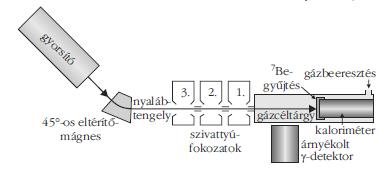
7. ábra. A 3He(α,γ)7Be reakció vizsgálatához a LUNA gyorsítónál
használt kísérleti elrendezés sematikus (nem mérethelyes) ábrája.
A céltárgymagok száma a céltárgygáz nyomásának és hőmérsékletének pontos mérésével, valamint a kamra méreteinek ismeretében egyszerűen kiszámítható. Ezzel kapcsolatban érdemes megemlíteni egy, nagy nyalábintenzitásoknál fellépő problémát, a céltárgygáz nyaláb okozta melegedésének hatását. Ahogy a nagy intenzitású nyaláb áthalad a céltárgygázon, lokálisan, a nyalábtengely mentén felmelegíti azt, aminek hatására a gáz sűrűsége csökken, tehát csökken a nyaláb által "látott" céltárgymagok száma. Ezt az effektust a céltárgymagokon rugalmasan szóródó 4He magok detektálásával sikerült megmérnünk és az eredmények analízisénél figyelembe vennünk.
Ahogy a nyaláb áthalad a céltárgygázon, lezajlik a 3He(α,γ)7Be reakció, ami a 4. ábrán feltüntetett prompt gamma-sugárzások kibocsátásával jár. Ezeket a gamma-sugarakat a céltárgykamrán kívül, annak közvetlen közelében elhelyezett, nagy hatásfokú germániumdetektorral mértük. A föld alatti laboratóriumban ugyan szinte elhanyagolható a kozmikus eredetű háttérsugárzás, ám a minden anyagban (így például a laboratóriumot körülvevő kőzetekben) megtalálható radioaktív izotópok alacsony energiás gamma-sugárzást bocsátanak ki, ez méréseinkhez zavaró hátteret ad. Ennek kiküszöbölésére a detektort a teljes 4π térszöget bezáró vastag (több mint 3 tonna) ólomárnyékolással vettük körül.
A reakcióban keletkező 7Be magok a reakciókinematika által meghatározott szűk nyílásszögű kúpon belül, a nyalábbal megegyező irányban repülnek tovább. A ritka gázban elérik a kaloriméter felszínét, amibe meghatározott mélységig behatolnak. Egy adott energiájú besugárzás után a kaloriméter felszínéről eltávolítottuk az azt fedő rézsapkát és a benne összegyűjtött 7Be magokkal együtt egy másik, szintén árnyékolt Ge detektor elé helyeztük, hogy a 7Be bomlásból származó gamma-sugárzást detektálhassuk. Így egy adott besugárzás során mindkét módszerrel meg tudtuk határozni a hatáskeresztmetszetet.
Azt, hogy milyen bombázó energiatartományban végeztük el a kísérleteket a gyorsító maximális energiája és a legkisebb mérhető hatáskeresztmetszet szabta meg. A legnagyobb elérhető 400 keV-es energiáról indulva fokozatosan csökkentettük az energiát, és végül 220 keV volt az a legalacsonyabb energia, ahol még kiértékelhető eredményt kaptunk. Érdemes megjegyezni, hogy a legalacsonyabb energián a besugárzás 40 napig tartott, ezalatt a céltárgyat mintegy 4 · 1021 darab 4He atom bombázta, mégis csak mindössze 5 · 105 reakció játszódott le. Ez is jelzi, milyen alacsony hatáskeresztmetszetek mérése volt a feladat.
Eredményeinket - az 5. ábrán már használt formátumban - a 8. ábra mutatja (több más, újabb mérés eredményeivel együtt, amelyekre még kitérek). Az ábra bal felső részén látható LUNA eredmények azt mutatják, hogy sikerült elérnünk mindhárom kitűzött célt [6, 9]. Egyrészt a föld alatti laboratóriumban végzett mérésekkel alacsonyabb energiákat sikerült elérnünk, mint korábban bármikor. Másrészt méréseink pontossága is jobb, mint az 5. ábrán bemutatott mérések esetén, az egyedi pontok hibája az igen alacsony hatáskeresztmetszet ellenére sem haladja meg az 5%-ot. Harmadrészt a prompt és aktivációs módszerrel végzett mérések eredményei hibahatáron belül megegyeznek, tehát méréseink nem erősítik meg a korábbi eredmények által mutatott különbséget.
Az ábrán folytonos vonallal egy elméleti számítás eredménye látható, amely a LUNA kísérleti adatokra lett normálva. Ilyen elméleti számítások segítségével lehet az S-faktor értékeket a kísérletileg elérhetetlen, Napra jellemző energiákra extrapolálni. Az alacsony energiás és nagy pontosságú LUNA méréseknek köszönhetően ez az extrapoláció elvben sokkal megbízhatóbbá vált. A LUNA mérésekhez rögzített elméleti görbe ráadásul kiválóan illeszkedik a lényegesen magasabb energián, Nara Singh és munkatársai által 2004-ben publikált értékekhez (lásd az ábrán). Éppen ezért a LUNA adatok 2007-es publikációjában például azt írtuk, hogy "méréseink hatására a Napból érkező 8B neutrínók számított fluxusának 3He(α,γ)7Be reakcióból eredő bizonytalansága 7,5%-ról 2,4%-ra csökkent" [9]. Az azóta eltelt három év fejleményei azonban sajnos megkérdőjelezték ezen állítás igazát.
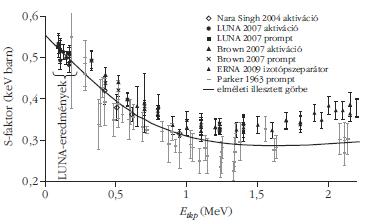 8. ábra. A 3He(α,γ)7Be reakció mért asztrofizikai S-faktora a tömegközépponti energia függvényében. Az új kísérleti eredményeken kívül csak Parker és munkatársai által 1963-ban publikált mérés eredményei láthatók, mivel ez az adatsor terjed ki magas energiákig. Folytonos vonallal a LUNA adatokra illesztett elméleti görbe látható. Az új eredmények pontos bibliográfiai adatait lásd az ERNA eredményeket bemutató [10] hivatkozásban. |
Az elméletileg számított S-faktor görbe alakja (energiafüggése) többé-kevésbé általánosan elfogadott volt a legutóbbi időkig, mindössze abszolút értékét illesztették a kísérleti adatokhoz (mint a 8. ábrán a LUNA adatokhoz), bár e normálás jogossága elméletileg megkérdőjelezhető. Természetesen más görbealakot jósló elméleti modellek is napvilágot láttak, de a régi kísérleti adatok nagy pontatlansága és szórása miatt kísérleti alapon nem lehetett dönteni közöttük. A 2000-es évek új eredményei azonban átalakították ezt a képet. A LUNA eredmények publikálását követően hamarosan napvilágot láttak a Brown és munkatársai által mindkét módszerrel végzett mérés eredményei (lásd a 8. ábrán). A mért pontok láthatóan fölé esnek a LUNA adatokra illesztett görbének, de a pontok hibáját tekintve az egyezés akár még elfogadható is lehetne. 2009-re azonban megszületett egy újabb kísérleti eredmény. A németországi bochumi egyetemen működő ERNA izotópszeparátorral egy új módszerrel vizsgálták a 3He(α,γ)7Be reakciót. Az ATOMKI kutatói ebben a mérésben is részt vettek, de a részletek bemutatásától most eltekintek. A mérés lényege az volt, hogy a reakcióban keletkező 7Be magokat közvetlenül (tehát nem a bomlásukon keresztül) detektálják oly módon, hogy a reakciótermékeket egy izotópszeparátoron vezetik keresztül. Ezzel a módszerrel csak nagyobb energián volt vizsgálható a reakció, de itt az eredmények meglepőnek bizonyultak [10]. Magas (körülbelül 1,3 MeV fölötti) energiákon korábban csak Parker és munkatársai vizsgálták ezt a reakciót, így az elméleti görbék ezt az adatsort próbálták reprodukálni. Most az ERNA mérések eredményei jóval magasabb S-faktor értékeket mutatnak, valamint jelentősen eltérő energiafüggést. Mivel magas energián csak a két említett, egymásnak ellentmondó adatsor létezik, mindenképpen szükséges új, független kísérleteket végezni ebben az energiatartományban. Ilyen mérést tervezünk az ATOMKI-ban is aktivációs technikával. Ezen kívül a reakció elméleti leírásában is szükséges a fejlődés, hogy az új kísérleti eredményeket értelmezni tudjuk és segítsük az alacsony energiákra történő extrapolációt.
A 3He(α,γ)7Be reakció a nukleáris asztrofizika egyik legfontosabb reakciója. Fontos szerepet játszik mind az Ősrobbanást követő elemszintézisben, mind a Nap és a hozzá hasonló csillagok hidrogénégési folyamataiban, és ezen keresztül a nagyenergiás neutrínók kibocsátásában. A 20. század második felében számos kísérletben mérték a reakció hatáskeresztmetszetét, de a mérések pontossága elmaradt a kívánatostól. Az utóbbi évtizedben ezért számos új mérést végeztek az adatok pontosításának érdekében. Ezek közül egyik legfontosabb a LUNA együttműködés által föld alatti laboratóriumban elvégzett mérés, amiben minden eddiginél alacsonyabb energiákat sikerült elérni. Az Ősrobbanásra jellemző energiatartományban új, pontos kísérleti értékek állnak rendelkezésre, így kijelenthetjük, hogy a 7Li probléma a 3He(α,γ)7Be reakció alapján nem oldható meg. A legújabb, nagyenergiás mérések azonban a reakcióval kapcsolatban új problémákat vetettek fel, ami kérdésessé teszi a Nap hidrogénégésére jellemző energiákra való extrapoláció megbízhatóságát. Ezért a 3He(α,γ)7Be reakció vizsgálata mind kísérleti, mind elméleti szempontból valószínűleg még hosszú ideig nem tekinthető lezártnak.
_______________________
1 Az S-faktor az asztrofizikában gyakorta használt mennyiség töltött részecskék között lejátszódó magreakciók jellemzésére. Előnye, hogy energiafüggése sokkal kisebb, mint magáé a hatáskeresztmetszeté, így ábrázolása is egyszerűbb. Ha az 5. ábra pontjait hatáskeresztmetszet formájában ábrázoltuk volna, akkor az értékek sok nagyságrendet fogtak volna át, így még logaritmikus skála alkalmazásával is nehéz lett volna különbséget tenni a különböző pontok között.