Fizikai Szemle honlap |
Tartalomjegyzék |
Kis Tamás
Eötvös József Középiskola, Heves
"A templomtoronyból egyszerre ejtünk le két egyenlő térfogatú fa- és ólomgolyót.
Tanítványaimmal e feladat megoldása volt a témánk néhány fizikaszakkörön a hevesi Eötvös József Középiskolában. Írásomban tapasztalatainkat foglaltam össze.
Vizsgáljuk a golyóra ható erőket! Lefelé irányul a nehézségi erő (mg), felfelé pedig a közegellenállási erő (Fk ) és a felhajtóerő (Ff ). Newton II. törvénye alapján a következő mozgásegyenletet írhatjuk fel:
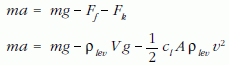
A közegellenállási erő kis sebességeknél nem a sebesség második hatványával arányos, hanem attól lineárisan függ. A golyók ugyan álló helyzetből indulnak, de egy toronyból való esés során a négyzetes függés dominál, tehát nem okoz nagy hibát, ha az elsőfokú résztől eltekintünk. - A felírt összefüggésből a gyorsulás kifejezhető:
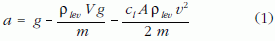
Mivel a mozgás során a sebesség (az állandó, egyensúlyi értékhez aszimptotikusan közeledve) nő, ezért a gyorsulás sem lehet állandó, a képletben minden más konstans.
Miben különbözik két azonos méretű, de eltérő sűrűségű golyó gyorsulása? A vizsgálathoz kerestünk két alkalmas, nagyon hasonló felületű golyót: az egyik fából, a másik vasból készült.
Ezek jellemzői: rfa = rvas = 0,025 m; mfa = 0,050 kg; mvas = 0,533 kg. Egyéb adatok: ρlev = 1,29 kg/m3 (a levegő sűrűsége 0 °C-on), cl = 0,45 (a golyó légellenállási tényezője).
Ezeket az értékeket behelyettesítve az (1) egyenletbe, a két golyó gyorsulására a következő összefüggést kapjuk:
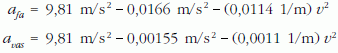
Eltérés a közegellenállásból és a felhajtóerőből származó tagnál tapasztalható, bár ez utóbbi hatása csak a fagolyónál befolyásolja némileg a gyorsulást. Ezt figyelembe véve:
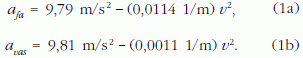
A golyó sebességének növekedése tehát a gyorsulás csökkenését okozza. A sebesség addig változik, amíg a gyorsulás jó közelítéssel 0 m/s2 nem lesz. Ezután a golyó gyakorlatilag az elért maximális sebességgel egyenletesen halad tovább. Ez az (1a) és (1b) egyenletekből kiszámítható:
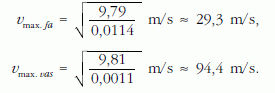
Látható, hogy a vasgolyó nagyobb sebességet érhet el. Továbbá az (1a) és (1b) egyenlet szerint a közegellenállásból származó tagban a v2 együtthatója a vasgolyó esetén körülbelül egy nagyságrenddel kisebb a fáénál. Mindebből arra következtethetünk, hogy a fagolyó sebessége a mozgás során végig kisebb. Tehát a vasgolyó ér előbb földet! Általánosítva is kimondhatjuk: azonos méretű golyók közül a legnagyobb sűrűségű ér le hamarabb.
Meg lehet-e adni az esés tetszőleges pillanatában a golyók sebességét, illetve gyorsulását? - Erre a kérdésre nem is olyan egyszerű válaszolni, hiszen a mozgás során mindkét mennyiség változik. A megoldáshoz tudnunk kell, hogy a sebesség a megtett út idő szerinti első, a gyorsulás pedig második deriváltja. Ez alapján az (1a) és (1b) egyenletek a következő alakba írhatók (mértékegységek nélkül):
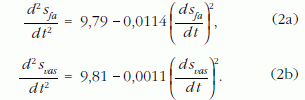
Az így kapott differenciálegyenletekben a két golyó út-idő, azaz s (t) függvénye az ismeretlen. Az egyenletekhez tartozik még két kezdőfeltétel, amelyek a golyók eredeti helyét és sebességét adják meg:
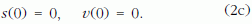
A mozgásegyenletekből származó differenciálegyenletek megoldása néhány ritka kivételtől (például szabadesés, harmonikus rezgőmozgás) eltekintve nagyon nehéz.
A problémát a Mathematica nevű programmal oldottuk meg az alábbiak szerint:

Az eredményül kapott függvények természetesen ábrázolhatók. A grafikonokat a jobb tanulmányozhatóság érdekében célszerű hosszabb idejű esésekhez (például 20 s) készíteni. Az út-idő függvények és a grafikonjaik:
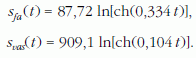
A két golyó közti távolság rohamosan nő. Például 5 s-os esési időnél, vagyis 117,5 m magas torony esetén a vasgolyó 28,7 m-es "előnnyel" ér földet (1. ábra).
A sebesség-idő függvények és a grafikonjaik:
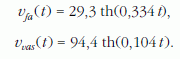
A két függvény végtelenben vett határértéke megegyezik a korábban, elemi úton meghatározott vmax.fa és vmax.vas értékekkel, ami elgondolásaink helyességére utal (2. ábra).
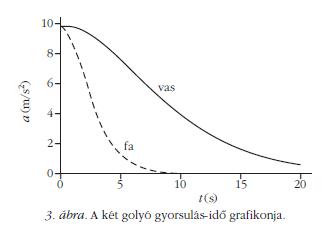
A gyorsulás-idő függvények és a grafikonjaik:
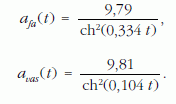
A fagolyó gyorsulása 8-10 s után erősen közelít 0-hoz, és ettől kezdve a mozgása egyenletesnek tekinthető. A vasgolyónál ez 25-30 s elteltével következik be (3. ábra).
A mozgás további elemzésében sokat segít, ha elkészítjük az út-idő függvények inverzét: s-1(t) := t(h), amivel a torony magasságának ismeretében kiszámítható a golyó esésének ideje. A képlet meghatározásához a következő parancssort kell beírni a Mathematica programba:

Az eredményül kapott inverzfüggvények:
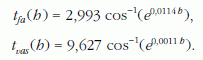
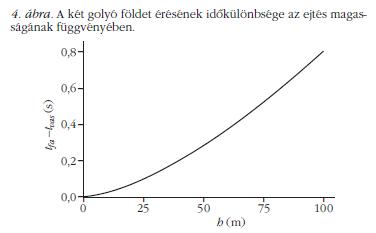
Ezek különbsége megadja, hogy mennyi idő telik el a golyók földet érése között: Δt (h) = tfa (h)-tvas (h). Az így kapott függvény grafikonja a 4. ábra.
 |
 |
Végezetül már "csak" az a feladat maradt, hogy valós körülmények között teszteljük eredményeinket ... Engedélyt kaptunk arra, hogy Heves város legmagasabb építménye, a Víztorony tetejéről, 37,5 m magasságból ejthessük le a golyókat. Alkalmas eszköz hiányában nem volt lehetőségünk az esési idő pontos meghatározására, ezért más mérési eljárásokat kellett kidolgoznunk. A kísérletet kellemes 19-21 °C-os, szélcsendes időben végeztük el (1. kép).
A testek távolságának mérése egy ismert helyzetben
Először határozzuk meg, hogy mekkora előnnyel ér le a vasgolyó! A t (h) függvénnyel kiszámítható a vasgolyó mozgásának ideje a földet érésig: tvas (37,5 m) = 2,784 s. Ennyi idő elteltével a golyók távolsága
d = 37,5 m - sfa (2,784 s) = 4,03 m.
A méréshez le kell fényképezni a golyók esésének utolsó 5-6 méterét úgy, hogy a vasgolyó már közvetlenül a talaj fölött legyen és a képen a fagolyó is feltűnjön. A feladat nem volt egyszerű, hiszen a golyók sebességéből adódóan a felvételre körülbelül 0,02 s áll rendelkezésre! A torony aljában mérőskálát állítottunk fel: egy 2 m magas fehér paravánra 10 cm-enként 1 dm széles fekete csíkokat ragasztottunk. Az így elkészült "méterrúd" elé ejtettük a golyókat. Ezzel lehetővé vált a golyók távolságának meghatározása. 12 ejtést végeztünk a toronyból. Az elkészített körülbelül 60 darab fénykép közül egy olyat találtunk, ami a feltételeknek megfelelt (2. kép ). A kiértékelés során azt tapasztaltuk, hogy a golyók távolsága d = 5,05 m (emlékeztetőül, a számított érték: 4,03 m).
A testek földet érése között eltelt idő mérése
Ezt az időtartamot közvetlenül kiszámíthatjuk a Δt(h) függvény segítségével: a Víztoronyból való ejtés esetében
Δt (37,5 m) = 0,185 s.
A golyók mozgását videokamerával is rögzítettük. A földet érést kísérő koppanások jól hallhatóak a felvételen, így a köztük eltelt idő számítógépes hangelemzéssel ms pontossággal mérhető. A 7 kiértékelt ejtésnél ez az időtartam: Δt = 0,190 ± 0,007 s-nak adódott (emlékeztetőül, a számított érték: 0,185 s).
<>
A két mérés egyértelműen megmutatta, hogy helytálló volt az elméleti úton nyert "jóslatunk", hiszen a kapott eredmények elég közel estek egymáshoz. Természetesen az is nyilvánvaló, hogy ennél több mérést kellett volna elvégeznünk ahhoz, hogy az elméleti úton kapott eredményeinket alaposabban "teszteljük" (többféle magasságból más méretű golyók ejtésével). De ez már meghaladta a szakkör kereteit. A célunkat így is bőven teljesítettük: sokat tanultunk és jól szórakoztunk!
____________________________
Köszönet a segítségért: Barna András és Egyed László tanár úrnak, Jakab Tibor fotóművésznek, valamint Balogh László és Marsi László úrnak a Heves Megyei Vízmű Rt.-től.