Fizikai Szemle 2011/6. 181.o.
EREDMÉNYEK, FEJLŐDÉSI IRÁNYOK
A HADRONFIZIKÁBAN
Fényes Tibor
MTA ATOMKI, Debrecen
Látható világunk elemi részecskékből, kvarkokból és
leptonokból épül fel. A kvarkokból összetett legegyszerűbb
részecskék a mezonok és barionok, közös
néven hadronok. A mezonok egy kvark – egy antikvark
párból, a barionok három valenciakvarkból
állnak. Mivel hat kvark (u, d, s, c, b, t) és hat antikvark
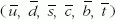 létezik, a hadronok sokféle
kombinációban épülnek fel. Az azonos (vagy nagyon
hasonló) kvarkösszetételű mezonoknak gyakran
külön nevet is adtak. Így 2010-ben már több, mint 150
mezon- és több, mint 130 barionállapot volt ismeretes.
A hadronokat tömegeikkel, összetételükkel és
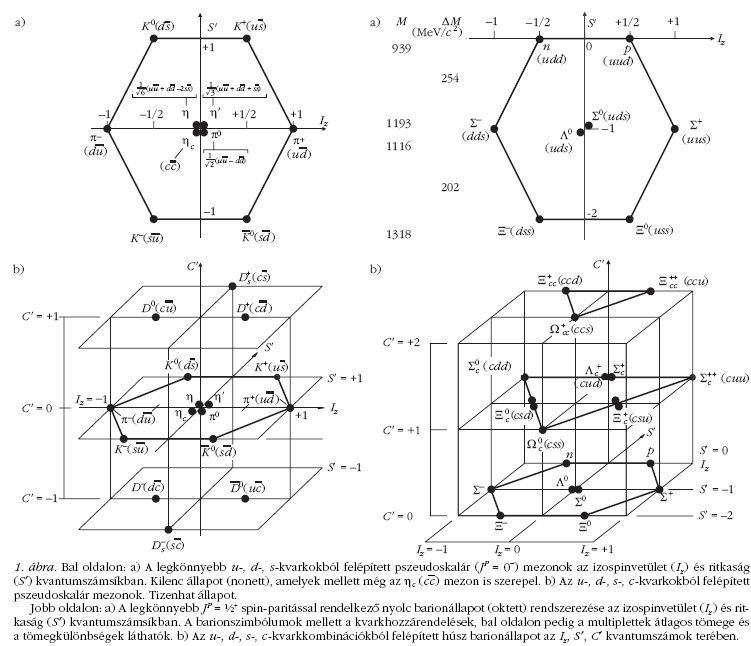
különböző kvantumszámaikkal lehet jellemezni. Illusztrációként
az 1. ábrán fel van tüntetve néhány
mezon- és barionállapot az Iz izospinvetület-, S? ritkaság-
és C? bájkvantumszám-térben a kvarkösszetételükkel
együtt. Teljesebb áttekintés található a Particle
Data Group [1] közleményben.
létezik, a hadronok sokféle
kombinációban épülnek fel. Az azonos (vagy nagyon
hasonló) kvarkösszetételű mezonoknak gyakran
külön nevet is adtak. Így 2010-ben már több, mint 150
mezon- és több, mint 130 barionállapot volt ismeretes.
A hadronokat tömegeikkel, összetételükkel és
különböző kvantumszámaikkal lehet jellemezni. Illusztrációként
az 1. ábrán fel van tüntetve néhány
mezon- és barionállapot az Iz izospinvetület-, S? ritkaság-
és C? bájkvantumszám-térben a kvarkösszetételükkel
együtt. Teljesebb áttekintés található a Particle
Data Group [1] közleményben.
A hadronok vizsgálata több szempontból is fontos.
Ma már általánosan elfogadott, hogy az erős kölcsönhatás
alapvető elmélete a kvantumszíndinamika
(QCD). A kvark-antikvark kölcsönhatás természete
pedig elsősorban a nehéz mezonok (közös néven
kvarkóniumok, 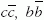 ) sajátságaiból,
valamint a szóráskísérletekből
ismerhetők meg. A helyzet hasonló a
magfizika őskorához, amikor az atommagot összetartó
erők felderítése céljából az egy protont és egy
neutront tartalmazó deuteron sajátságait kezdték tanulmányozni.
) sajátságaiból,
valamint a szóráskísérletekből
ismerhetők meg. A helyzet hasonló a
magfizika őskorához, amikor az atommagot összetartó
erők felderítése céljából az egy protont és egy
neutront tartalmazó deuteron sajátságait kezdték tanulmányozni.
Másrészt a hadronok a legegyszerűbb elemi kvarkokból
felépülő részecskék, sajátságaik megismerése
nagyban elősegíti a bonyolultabb rendszerek (atommagok,
atomok, molekulák stb.) megértését is.
A jelen közlemény néhány fontosabb kísérleti és
elméleti eredményről ad számot a hadronfizika területéről.
Ezek a következők: a hadronok szerkezete és
eredő spinje; a hadronok gerjesztett állapotai; rács-
QCD számítások; a hadronok kölcsönhatásai; hadronfizikai
laboratóriumok, a kutatások fejlődési irányai.
A hadronok szerkezete
A hadronok szerkezetével kapcsolatban több kérdés
is megválaszolásra vár. Például milyen a valenciakvarkok
térbeli eloszlása; milyen a kvarkok és az erős
kölcsönhatást közvetítő gluonok dinamikája; hogyan
alakul ki a hadron spinje; milyen a tengerkvarkok
összetétele és milyen a hozzájárulásuk a hadronok
észlelhető sajátságaihoz stb.
A hadronok szerkezete különböző reakciókkal tanulmányozható.
Igen nagy energiájú (kemény) reakcióknál
(< 0,1 fm távolságoknál) perturbációs számítás
alkalmazható, > 1 fm távolságoknál (lágy reakcióknál)
azonban ez a számítási mód nem működik.
Szerencsére faktorizálhatók a formulák, ami azt jelenti,
hogy a nagy impulzusú (perturbatív) és alacsony
impulzusú (nem perturbatív) oldalai a kölcsönhatásoknak
világosan elválaszthatók.
A hadronok szerkezetének tanulmányozására sokféle
reakciót használnak:
pp, 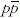 rugalmas szórás,
rugalmas szórás,
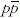 → l +l- X Drell–Yan-folyamat,
l = lepton,
→ l +l- X Drell–Yan-folyamat,
l = lepton,
lepton + N→ lepton + X mélyen rugalmatlan szórás
(DIS),
llepton + N → lepton + hadron + X félig inkluzív
mélyen rugalmatlan szórás,
γp → p?π, ρ, ω, … általánosított partoneloszlási
(GPD) reakciók stb.
A következőkben csak a proton szerkezetére, valamint
a proton spinjének megértésére vonatkozó vizsgálatokat
tárgyaljuk részletesebben.
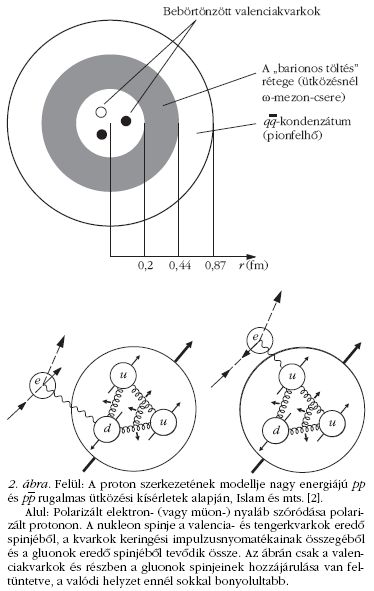
A proton szerkezetét nagyenergiájú pp, 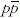 rugalmas szórási kísérletekben már évtizedek óta vizsgálják
a CERN-ben és a Fermi-laboratóriumban, néhányszor
tíz GeV-től 1,8 TeV-ig terjedő tömegközépponti
energia (s 1/2) tartományban. E rugalmas szórási vizsgálatok
alapján a protonban három réteget lehet megkülönböztetni
(2. felső ábra).
rugalmas szórási kísérletekben már évtizedek óta vizsgálják
a CERN-ben és a Fermi-laboratóriumban, néhányszor
tíz GeV-től 1,8 TeV-ig terjedő tömegközépponti
energia (s 1/2) tartományban. E rugalmas szórási vizsgálatok
alapján a protonban három réteget lehet megkülönböztetni
(2. felső ábra).
Az első, ~0,2 fm sugarú gömbben van a három valenciakvark
bebörtönözve. Ebben a tartományban a
pp rugalmas szórás úgy jön létre, hogy az egyik proton
valenciakvarkja ütközik a másik proton valamelyik
valenciakvarkjával "kemény" ütközésben, ahol az
átadott négyesimpulzus-négyzet |t| ~ 4 GeV2 (a részecskefizikában
használatos ħ = 1, c = 1 egységekben)
vagy nagyobb.
A második ~0,44 fm (külső) sugarú réteg "barionos
töltés" nevet visel. pp- vagy
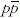 -ütközéseknél e rétegek
között ω vektorbozoncsere történik, az átadott
négyesimpulzus-négyzet |t| ~ 1 és 4 GeV2 között
van. Az 1-es spinű ω-mezon cseréje analóg azzal,
mint amikor egy elektromos töltést fotoncserével
vizsgálunk.
-ütközéseknél e rétegek
között ω vektorbozoncsere történik, az átadott
négyesimpulzus-négyzet |t| ~ 1 és 4 GeV2 között
van. Az 1-es spinű ω-mezon cseréje analóg azzal,
mint amikor egy elektromos töltést fotoncserével
vizsgálunk.
A harmadik réteg külső sugara ~0,87 fm, ami egyben
a proton töltéssugara. E réteg kis |t| tartományban
vizsgálható, közel egyenes irányban a bombázó
nyalábokkal. E szórásnál a proton külső rétegében
lévő 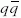 -kondenzátum (pionfelhő) hat kölcsön a
másik proton hasonló rétegével, ami diffraktív szóráshoz
vezet. Kis |t| tartományban (0 és 1 GeV2 között)
pp-szórásnál a Coulomb- és erős kölcsönhatások között
interferencia lép fel.
-kondenzátum (pionfelhő) hat kölcsön a
másik proton hasonló rétegével, ami diffraktív szóráshoz
vezet. Kis |t| tartományban (0 és 1 GeV2 között)
pp-szórásnál a Coulomb- és erős kölcsönhatások között
interferencia lép fel.
Különböző modellek alapján leírható, hogy hogyan
alakul a dσ/dt differenciális hatáskeresztmetszet a pp-szórásban
az átadott négyesimpulzus-négyzet |t|
függvényében. Külön-külön számították a hatáskeresztmetszetet
valencia qq, ω-mezon csere és diffrakciós
szórásra (Islam és mts. [2]).
A CERN-i nagy hadronütköztető (LHC) lehetőséget
ad arra, hogy a pp-szórási vizsgálatokat 14 TeV tömegközépponti
energiáig kiterjesszék. E célra létrehozták
a TOTEM (TOTal cross-section, Elastic and
diffracion scattering Measurement) berendezést (Bressan,
Greco [3]), amivel 0–10 GeV2 |t| tartományban
vizsgálják a rugalmas szórási hatáskeresztmetszeteket.
A rugalmas szórási és (legtöbb) diffraktív eseményben
a végállapoti proton kis szögben repül a bombázó
nyalábhoz képest, ami speciális detektorrendszer kifejlesztését
kívánta meg.
A proton szerkezetének várható pontosabb felderítése
analóg lesz azzal, mint amikor Rutherford és
munkatársai 1911-ben feltárták az atom szerkezetét
α-részecskék szóródásának vizsgálata alapján.
A nukleonok spinje 1/2. Jelenlegi ismereteink szerint
ez a spin a) a valenciakvarkok, tengerkvarkok (és
antikvarkok) spinjeinek eredőjéből, b) a kvarkok keringési
impulzusnyomatékainak összegéből és c) a
gluonok hozzájárulásából tevődik össze.
A SLAC (Stanford) laboratórium úttörő kísérletei
nyomán a CERN-i EMC (European Muon Collaboration)
kutatócsoport arra a meglepő következtetésre
jutott, hogy a kvarkspinek csak viszonylag kis hozzájárulást
adnak a proton spinjéhez. Az eredményeket
megerősítették a CERN-i második generációs, továbbá
a SLAC- és DESY- (Hamburg) kísérletek is: a valenciaés
tengerkvarkok spinjei csak 30%-át adják a nukleon
spinjének. Ezt a felismerést szokták úgy emlegetni,
mint a spin-"krízis" kezdetét.
A kvarkok eredő spinje. A nukleon spinjére vonatkozó
kvarkszintű ismereteink elsősorban polarizált,
mélyen rugalmatlan szórási kísérletekből erednek.
Ezekben nagyenergiájú, a nyaláb mentén polarizált
elektronokkal vagy müonokkal vizsgálják a szintén
polarizált proton (neutron) szerkezetét. Azok az
elektronok, amelyeknek spinje a nyaláb irányába mutat,
majdnem kizárólag olyan kvarkokkal lépnek kölcsönhatásba,
amelyeknek ellentétes a spinbeállása.
Amikor a nyalábpolarizációt (vagy nukleonpolarizációt)
megfordítják, a leptonok más kvarkokkal lépnek
kölcsönhatásba és ilyenkor megváltozik a szórási
szög és energiaveszteség. A különbségből a kvarkspinek
aszimmetrikus beállására lehet következtetni. A
kísérletek szerint a proton u-valenciakvarkjainak
spinje ugyanolyan irányú, mint a proton egészének
spinje, míg a d-valenciakvark spinje ezzel ellentétes
(2. alsó ábra).
A COMPASS (CERN) és HERMES (DESY) eredmények
szerint a gluonpolarizáció kicsi vagy zéró.
Annak a lehetősége, hogy a nukleon hiányzó spinjének
többségét a gluonok hozzák létre, kizárható (Bradamanti
[4]).
A kvarkok keringési impulzusnyomatéka. A nukleon
tömege ~939 MeV/c2, ugyanakkor a nukleont
felépítő u- és d-valenciakvarkoké ≤ 7 MeV/c2. Mindez
arra utal, hogy a kvarkok a nukleonban valószínűleg
nagy sebességgel mozognak és az energia- (tömeg-)
tartalom jelentős része a kvarkok (keringési) mozgásából
eredhet. A kísérletek ezt alátámasztani látszanak.
A Jefferson-laboratóriumban (USA) végzett mérések
szerint a kvarkok keringési impulzusnyomatéka
az x Bjorken-változó nagy értékeinél (x ≥ 0,6) jelentős.
A DESY HERMES-együttműködésben a céltárgy
transzverzspin-aszimmetriáját mélyen rugalmatlan
Compton-szórással vizsgálták. Modellfüggő analízissel
sikerült meghatározni az u-kvark teljes impulzusnyomatékának
hozzájárulását a nukleonspinhez. Az előzetes
eredmények szintén jelentős hozzájárulásra
utalnak.
A nukleonokban a ritka- (s-) kvark a tengerkvarkok
között lehet jelen. Mind a Jefferson-laboratórium
HAPPEX, mind a DESY HERMES kísérletekben nyert
eredmények arra utalnak, hogy a ritka kvarkok hozzájárulása
a nukleonspinhez nagyon kicsi (vagy zéró). A
HERMES-eredmények szerint általában a tengerkvarkok
polarizációja nagyon kicsi.
A proton spinszerkezetét igen részletesen tárgyalja
Bass [5] összefoglaló munkája.
A hadronok gerjesztett állapotai és bomlásai
A hadronok gerjesztett állapotainak vizsgálatára többféle
berendezést is kifejlesztettek. Igen hatékonynak
bizonyult például a CERN-i lassított antiproton kísérletekben
felhasznált kristályhordó spektrométer.
Ennek fő eleme egy 1380 Cs(Tl) detektort tartalmazó
detektorrendszer, amit proporcionális kamrával és
jet-driftkamrákkal is kiegészítettek. A rendszer lehetőséget
ad a 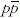 -megsemmisülés után előállt mezonok
tömegének és kvantumszámainak (I izospin,
J spin, P paritás, C töltéstükrözéses paritás)
meghatározására. A programban magyar
kutatók is eredményesen vettek részt
(Hidas [6]).
-megsemmisülés után előállt mezonok
tömegének és kvantumszámainak (I izospin,
J spin, P paritás, C töltéstükrözéses paritás)
meghatározására. A programban magyar
kutatók is eredményesen vettek részt
(Hidas [6]).
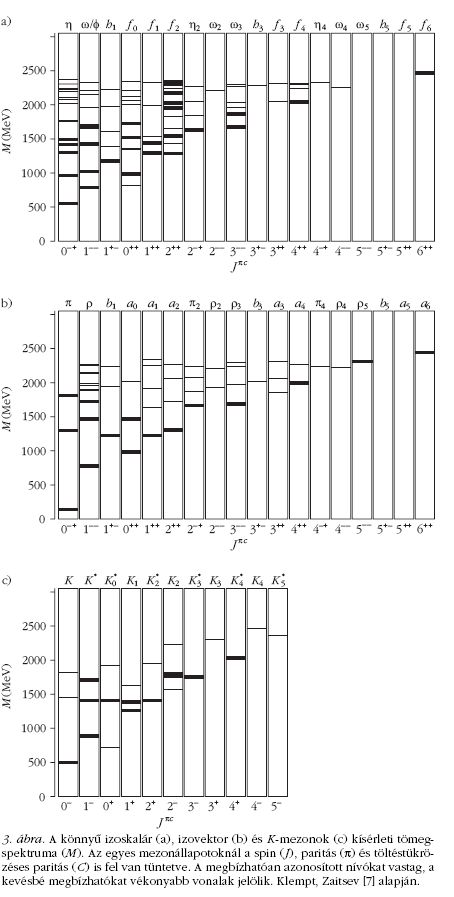
Mezonok
A különféle mezonok gerjesztett állapotairól
áttekintő képet ad a 3. ábra.
Az utóbbi évtizedekben a kvantum-színdinamika
az erős kölcsönhatás elfogadott
elméletévé nőtte ki magát. Nagyobb távolságoknál
(≥0,2 fm) az erős kölcsönhatás
erőssége azonban olyan nagy, hogy a QCD
perturbációs módszereket már nem alkalmazhat.
Léteznek viszont olyan QCD által
sugallt modellek, amelyekkel a "lágy" hadronikus
és nukleáris folyamatok is sikerrel
tárgyalhatók.
Az elmélet feladata, hogy nem csak a
hadronok összetételét, hanem tömegét,
gerjesztéseit, reakcióit és bomlásait is értelmezze.
A hadronok dinamikájának leírására
több kvarkmodellt is kidolgoztak. A kvarkmodellek
felteszik, hogy a mezon összetevő
kvark-antikvark párból áll. A kvark
és antikvark tömegei a királis szimmetria
spontán sérüléséből származnak (6. alsó
ábra).
A kvarkmodellek legtöbbje tartalmazza a
következő elemeket:
A mezonban lévő kvark és antikvark
között fellép egy centrális kölcsönhatás,
ami azonos a QCD potenciáljával:
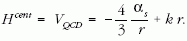
Itt αs az erős kölcsönhatás csatolási
paramétere, r a kvark-antikvark közti távolság,
k a bebörtönző potenciál állandója. A potenciál
első tagja a Coulomb-potenciálhoz
hasonlít, ennek létét a nagyenergiájú szóráskísérletek
igazolják. A VQCD potenciál
ilyen alakban történő felírását a 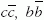 kvarkónium-mezonok gerjesztési spektrumai
is meggyőzően alátámasztják.
kvarkónium-mezonok gerjesztési spektrumai
is meggyőzően alátámasztják.
A mezonspektrumok értelmezéséhez
azonban azt is fel kell tételezni, hogy a
kvark és antikvark között fellép egy erős
Hss spin-spin kölcsönhatás. Ilyen kölcsönhatást az
analóg pozitróniumnál (az elektron és pozitron kötött
állapotánál) is észleltek, de ott ez csak gyenge, hiperfinom
felhasadást okoz az energianívókban. A mezonnál
a részecskék közötti távolság több nagyságrenddel
kisebb, így itt – mint azt a kvarkóniumokkal
kapcsolatos kísérletek mutatták – a spin-spin "kromomágneses"
kölcsönhatás igen erős és jelentős felhasadást
okoz. Ilyen felhasadás lép fel például az 1 1S0 és 1
3S1 állapotok között, ahol az 1S0
állapotban a kvarkspinek
ellentétes, a 3S1 állapotban azonos irányba mutatnak
([8]-ban az V.2.2. pont).
A mezonoknál spin-pálya kölcsönhatás is lehetséges
(HSL ), de ez általában kicsi.
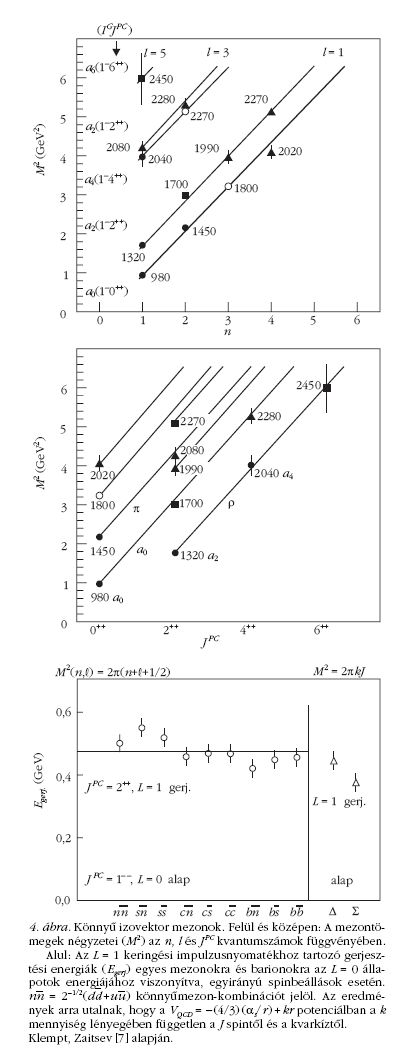
A bebörtönzési potenciálban (kr) szereplő k menynyiséget
általában függetlennek tekintik a spintől és
a kvarkok "íz"-étől (4. ábra középső, valamint alsó
része).
A ritka kvark tömege kicsivel nagyobb, mint az u- és
d-kvarké. Egyébként az összetevő kvarktömegek
szabad paraméterek.
Az izoskalár- (azaz nulla izospinű) mezonoknál a
különböző ízű konfigurációk keverednek, például 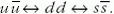 .
.
Főleg ezek az összetevők határozzák meg a hadronspektrumokat.
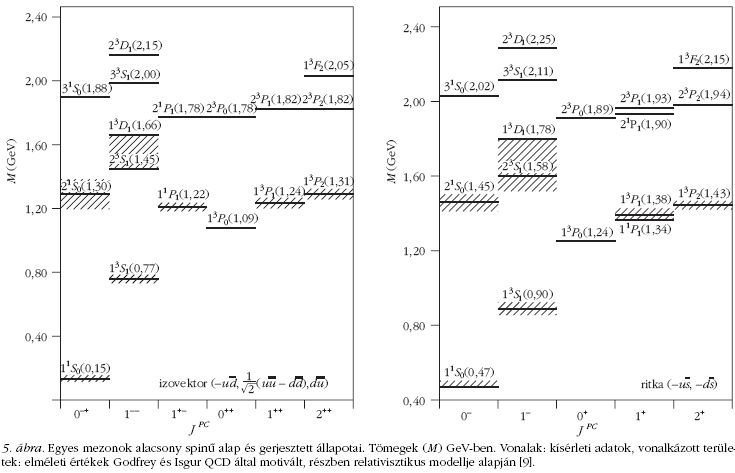
A spintől függő kölcsönhatást Godfrey és Isgur [9]
egy gluon cseréjére, Vijande és mts. Goldstone-bozon
cserére, a Bonn-kvarkmodellek (Koll és mts. 2000;
Ricken és mts. 2000) pedig instanton effektusokra
vezetik vissza. (Az instantonok közelítőleg úgy tekinthetők,
mint a QCD-vákuumban fellépő nem perturbatív
fluktuációk, amelyekben viszonylag kis térfogatban
nagyon erős terek jelennek meg. Közvetlen instanton
effektusok pszeudoskalár és skalár mezonoknál
várhatók. Bevezetésük például magyarázhatja,
hogy az η' mezonok tömege miért majdnem kétszerese
az η mezon tömegének. Az instant-on-vákuum elmélete
azonban még távolról sem lezárt.)
A felsoroltak közül csak a Godfrey–Isgur-modellt
tárgyaljuk részletesebben, mivel ez mind a mai napig
átfogó, referenciamodellnek számít. Létrejöttét a
kvantumszíndinamika motiválta és – eltérően a korábbi
modellektől – már relativisztikus effektusokat is
figyelembe vesz.
Godfrey–Isgur mezonmodellje. A modell szerint a
mezon dinamikája egy olyan "puha-QCD" Hamiltonoperátorral
írható le, amelyben rövid távolságoknál egy
gluon cseréje dominál, nagyobb távolságoknál pedig
egy íztől független Lorentz-skalár kölcsönhatás. A Hamilton-
operátor alakja (ħ = 1, c = 1 egységekben):
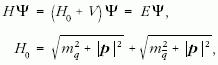
ahol 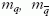 , a kvark, illetve antikvark nyugalmi
tömege, p a relatív impulzus tömegközépponti rendszerben,
, a kvark, illetve antikvark nyugalmi
tömege, p a relatív impulzus tömegközépponti rendszerben,
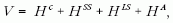
itt Hc a centrális potenciál, ami Coulomb-
kölcsönhatásból plusz a br+c típusú bebörtönző potenciálból
áll, ez utóbbit harmonikus oszcillátor potenciállal
közelítik, HSS a spin-spin kölcsönhatás, HLS a spinpálya
kölcsönhatás és HA a megsemmisülési kölcsönhatás,
ami a 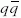 -megsemmisülés lehetőségét veszi
figyelembe gluonokon keresztül. Ez csak izoskalár mezonoknál lehet jelentős.
-megsemmisülés lehetőségét veszi
figyelembe gluonokon keresztül. Ez csak izoskalár mezonoknál lehet jelentős.
Az elmélet paraméterei a következők. Tömegek:
0,5(mu+md) = 220 MeV,
ms = 419 MeV, mc = 1628
MeV, mb = 4977 MeV; Λ = 200 MeV; a bebörtönző potenciál
b és c értékei és mások.
A modell alapján számíthatók a mezonok gerjesztett
állapotainak energiái (tömegei), kvantumszámai,
az állapotok hullámfüggvényei – például az
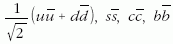
tartalom különböző radiális (n) kvantumszámoknál –,
az erős, elektromágneses, gyenge bomlási amplitúdók
és a töltéssugarak.
A gerjesztési spektrumokra példák láthatók az 5.
ábrán. Godfrey és Isgur [9] eredeti dolgozatában izoskalár,
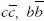 és más c- és b-kvark
tartalmú mezonokra
is vannak adatok. Számítottak továbbá parciális
bomlási szélességeket (például a ρ → ππ, φ → KK K* →
Kπ bomlásokra) és sok más mennyiséget is.
és más c- és b-kvark
tartalmú mezonokra
is vannak adatok. Számítottak továbbá parciális
bomlási szélességeket (például a ρ → ππ, φ → KK K* →
Kπ bomlásokra) és sok más mennyiséget is.
A modell nagy előnye más ad hoc leírásokkal
szemben, hogy egységes leírást ad a mezonok statikájára
és dinamikájára a legnehezebb Y ( )
mezonoktól
a könnyű pionokig. Az alacsonyan fekvő állapotok
energiáit elég jól leírja. A modell hátránya, hogy a
relativisztikus effektusokat csak félig kvantitatíven
veszi figyelembe (a Hamilton-operátor kimutathatóan
nem kovariáns), továbbá hogy gluonlabdákat és hibrid
állapotokat nem tartalmaz. Ez utóbbiak tárgyalására
a rács-QCD számításoknál visszatérünk.
)
mezonoktól
a könnyű pionokig. Az alacsonyan fekvő állapotok
energiáit elég jól leírja. A modell hátránya, hogy a
relativisztikus effektusokat csak félig kvantitatíven
veszi figyelembe (a Hamilton-operátor kimutathatóan
nem kovariáns), továbbá hogy gluonlabdákat és hibrid
állapotokat nem tartalmaz. Ez utóbbiak tárgyalására
a rács-QCD számításoknál visszatérünk.
Barionok
A barionok gerjesztett állatpotainak és bomlásainak
leírására is rendelkezésre állnak modellek. Sikeres és
átfogó volt Isgur és Karl QCD által motivált nem-relativisztikus
modellje, amit később részben relativisztikussá
fejlesztettek (Capstick, Isgur). Rendelkezésre áll
továbbá a félrelativisztikus fluxuscsőmodell, az instantoneffektusokra,
Goldstone-bozon (pion-) cserére
alapozott modellek, valamint az algebrai kollektív
modell is. Mindezekről jó összefoglalást ad Capstick
és Roberts [10] munkája.
Capstick és Isgur részben relativisztikus barionmodellükben
feltételezik, hogy a barion három véges
kiterjedésű összetevő (constituent) kvarkból áll, amelyek
tömege 220 MeV (a könnyű kvarkokra), illetve
420 MeV (a ritka, s-kvarkra). A modell Schrödinger-egyenletében
szereplő Hamilton-operátor
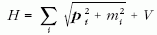
alakú, ahol V a relatív helyzettől és impulzustól (p)
függő potenciál. Ez nem relativisztikus határesetben a
következő tagokból áll:
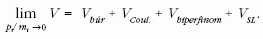
Itt Vhúr = ∑i bli+c, ahol
b a húr feszültsége, li az i-edik
kvark távolsága a húr csomópontjától, c állandó, VCoul
a Coulomb, Vhiperfinom a hiperfinom, VSL a spin-pálya
kölcsönhatás potenciálja.
A Hamilton-operátor mátrixot nagy harmonikus
oszcillátor alapon feszítették ki, majd a mátrixot diagonalizálva
adatokat nyertek az N, Δ, Λ, ∑ rezonanciák
tömegeire széles spin-paritás tartományokban. Számították
továbbá a hullámfüggvényeket és a nukleonok
és Δ rezonanciák Nπ bomlási amplitúdóit is. Ez utóbbiak
négyzete határozza meg az Nπ bomlási szélességet,
a Γ-t.
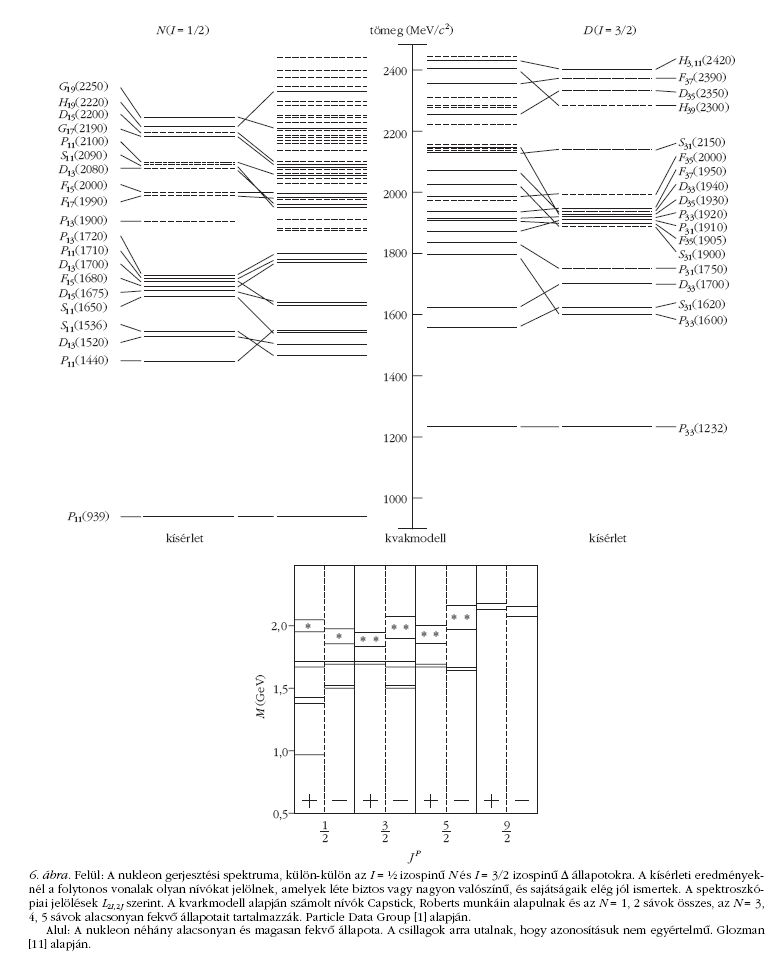
A 6. felső ábra bemutatja a nukleon gerjesztési
tömeg (MeV/c ) 2
spektrumát külön-külön az I = 1/2 izospinű N és I =
3/2 izospinű Δ állapotokra. A kvarkmodell alapján
számított elméleti értékek Capstick, Roberts [10] munkáin
alapulnak. Az elmélet 2,4 GeV gerjesztési energiáig
~45 N állapotot jósol, de csak 12-t sikerült megbízhatóan
és 7-et vagylagosan azonosítani a kísérletileg
észlelt nívókkal. Jelenleg több elektrongyorsítón
intenzív kutatómunka folyik a barion-rezonanciaspektrumok
alaposabb megismerésére. Elméleti oldalról,
ha létezne erősen kötött kétkvark-állapot, ez a
szabadsági fokok számát csökkentené és így alacsony
gerjesztési energiáknál kevesebb nívó lenne várható.
Ugyanakkor a Bijker, Iachello, Leviatan által javasolt
algebrai kollektív modell a spektrum alsó részében
még több nívót jósol. A kísérletileg észlelt nívók
száma még a kvark-kétkvark modellek által jósoltaknál
is jóval kevesebb.
Számították a nukleonok és Δ-rezonanciák Nπ, Nη,
Δη, Δπ, Nρ, ΛK, ∑K bomlási
szélességeit (Γ) is (Capstick, Roberts [10]).
Összefoglalóan az a következtetés vonható le,
hogy a felsorolt barionmodellek a barionok gerjesztett
állapotait elég jól leírják, gyakran különböző
szempontok alapján. Az egy gluon cseréjére alapozott
modell a legegyszerűbb és a spektrum ésszerű,
gazdaságos leírását adja. Szigorúan véve egyik modell
sem QCD alapon nyugvó, de QCD által motivált
és egyesek részben relativisztikusak. Az erős és
elektromágneses bomlási amplitúdók leírása azonban
már távolról sem olyan jó, mint a gerjesztési nívóké.
Ez több okra vezethető vissza: a kinetikusenergia-
tagra a Hamilton-operátorban, a tenzorerők és a
háromtest-erők jelenlétére vagy hiányára, a pion méretére
stb. A hullámfüggvények részleteire a bomlási
amplitúdók sokkal érzékenyebbek, mint a gerjesztési
spektrum.
A 6. alsó ábrán a nukleon néhány alacsonyan és
magasan fekvő állapota látható. Megfigyelhető, hogy
a magasan fekvő állapotokban az azonos spinű, de
ellenkező paritású nívók közel egyenlő tömeggel rendelkeznek.
A jelenség azzal magyarázható, hogy kis
gerjesztési energiáknál a valenciakvarkok erősen kötődnek
a kvarkkondenzátumhoz és így nagy az összetevő
(dinamikai) tömegük. Ekkor a valenciakvarkokat
nem-relativisztikus, kvázirészecskéknek lehet tekinteni.
Magasabb energiáknál azonban az azonos spinű,
de ellentétes paritású nívók energiája közel egyenlővé
válik, királis szimmetria érvényesül. Ez csoportelméleti
nyelven a QCD királis szimmetriájának visszaállását
jelenti nagyobb gerjesztési energiáknál.
Rács-QCD számítások hadronokra
Rács-QCD számítások a hadronok kötött állapotait az
elsődleges elvekből (a QCD Lagrange-energiasűrűségéből
vagy annak különböző közelítéseiből) kiindulva
írják le. A számításokban a téridő-kontinuumot
négydimenziós pontokból álló dobozzal közelítik. A
kvark- és gluonkvantumtereket csak a rácspontokon
(vagy annak összeköttetésein) vizsgálják. Így a QCD
egyenletei diszkretizálhatók, a deriváltakat véges differenciákkal
lehet helyettesíteni, ami egyszerűsítést
jelent az egyébként végtelenül nehéz probléma kezelésében.
A számítások többdimenziós integrálást kívánnak
az adott térben, amit Monte-Carlo-eljárással
végeznek. Ez a QCD-vákuumra olyan térkonfigurációkat
generál, amelyeknek legnagyobb a járuléka az
integrálhoz. Általában több száz konfiguráció szükséges,
hogy a Monte-Carlo-számításból eredő statisztikus
hibát 1% alá lehessen csökkenteni.
A rács-QCD számítást véges térfogatra és véges
rácsközre végzik. A számítások térfogattól való függése
gyorsan csökken a térfogat nagyobbodásával, általában
elég ~2,5 fm átmérőjű térfogatot figyelembe
venni. A rácspontok egymáshoz való közelítésével a
számítások nagyon elbonyolódnak. A fejlesztések
eredményeként ~0,1 fm rácspontközzel már elég jól
lehet közelíteni a kontinuum QCD-t. A módszer részletes
leírása található például Montvay, Münster [12]
közleményében, valamint [1]-ben további utalások.
A számításokban csak u-, d- és s-kvarkokat vesznek
figyelembe, mivel a c-, b- és t-kvarkok túl nehezek
ahhoz, hogy lényeges hatást gyakoroljanak.
Hosszú ideig problémát jelentett a dinamikus (vagy
másképpen tenger-) kvarkok figyelembe vétele, mivel
ezek a számításokat igen elbonyolították (például 107
dimenziójú mátrix inverzióját kívánták) és a költségeket
nagyon megnövelték. Az algoritmusok tökéletesítésével
és ~1015 művelet/s sebességű szuperszámítógépek
alkalmazásával azonban már ezek is figyelembe
vehetők.
A számításokban az u-, d- és s-kvarkok tömegei,
valamint az αs csatolási erősség bemenő paraméterek.
Általában felteszik, hogy mu, md <<
ms/2. Először
mind kísérletileg, mind elméletileg jól definiált
mennyiségeket számítanak ki (például a π-, K-, Ds-,
Y-mezonok tömegeit). E számításokkal lefixálják a
kvarktömegeket, majd ezeket használják fel a további,
új mennyiségek számításánál. A jelenlegi számításokban
nagyobb kvarktömegeket használnak, mint amilyenek
az u- és d-kvarkok reális (a QCD Lagrange-energiasűrűségében
szereplő) tömegei. Ennek fő oka,
hogy így sokkal kisebb számítógép-kapacitásra van
szükség. Növekvő számítógép-teljesítménnyel, az
algoritmusok javításával, a királis effektív elmélettel
való kapcsolat tökéletesítésével azonban remélhető,
hogy pár éven belül áthidalható lesz a rács-QCD számítások
és a fizikai kvarktömegek közötti rés. Nagyon
fontos a figyelembe vett véges térfogat és véges rácsközök
hatásának pontos ismerete. Csak ezek tisztázása
után remélhető, hogy megbízható következtetéseket
lehet levonni, például a kvark keringési impulzusnyomatékára,
az általánosított partoneloszlási (GPD)
függvényekre stb.
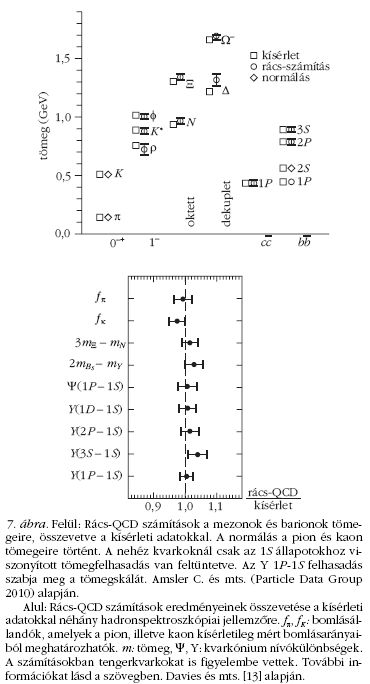
A hadrontömegekre vonatkozó rács-QCD elméleti
és kísérleti eredmények összevetése a 7. felső ábrán
látható. E számításokban dinamikai u-, d- és s-kvarkokat
is figyelembe vettek. A hadrontömegeket a számítások
elég jól reprodukálják.
A dinamikai (vagy másképpen tenger-) kvarkokat
is figyelembe vevő, néhány nem perturbatív rács-
QCD számítás eredménye a 7. alsó ábrán látható. Az
összes számított mennyiség néhány százalékon belül
konzisztensen egyezik a kísérleti adatokkal. Ez reményt
ad arra, hogy további mennyiségeket, például
a B- és D-mezonok leptonikus és félig leptonikus
bomlásainak hozamait, a Cabibbo–Kobayashi–Maskawa
(CKM) féle kvarkkeveredési mátrix elemeit, a gluonlabdák
és pentakvarkok sajátságait is megbízhatóan
lehessen számítani.
Figyelemre méltó, hogy a rács-QCD számítások az
erős (nukleáris) kölcsönhatás főbb vonásait is képesek
leírni, nevezetesen a rövid hatótávolságú taszítást
és a hosszabb hatótávolságú vonzást.
A kvarkok közötti kölcsönhatást gluonok közvetítik.
A gluonok színes objektumok, egymással is kölcsönhatásba
lépnek. A kvantum-színdinamikai (téridő-
rács) számítások szerint kialakulhatnak tisztán
gluonokból álló képződmények, gluoniumok (gluonlabdák)
is, például gg vagy ggg alakban, ahol is a
gluonok színei kioldják egymást. Az elmélet szerint a
gluonlabdák nagyon rövid ideig (nagyságrendileg
10-24 s) ideig élhetnek, de ez elegendően hosszú a
detektálhatóságukhoz.
A rács-QCD számítások szerint gluonlabda nem
csak alapállapotban fordulhat elő, hanem különböző
JπC értékeknél számos gerjesztett állapot is várható.
A QCD elmélet hibrid állapotok létét is megjósolja,
amelyekben mezon plusz extra gluon gerjesztés
lép fel.
Az ismert hadronok többsége 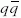 (mezon),
illetve
qqq (barion) kvarkösszetétellel rendelkezik. A QCD-számítások
szerint azonban elképzelhető például
mezon-mezon molekulák kialakulása is, amelyeket
"maradék" QCD-erők tartanak össze (analógiában az
atommag-molekulákkal). Létrejöhetnek színsemleges
(mezon),
illetve
qqq (barion) kvarkösszetétellel rendelkezik. A QCD-számítások
szerint azonban elképzelhető például
mezon-mezon molekulák kialakulása is, amelyeket
"maradék" QCD-erők tartanak össze (analógiában az
atommag-molekulákkal). Létrejöhetnek színsemleges
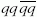 vagy
vagy
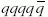 multikvarkállapotok is, és ezek
együtt jelentkezhetnek a szokásos mezon- és barionspektrumokkal.
multikvarkállapotok is, és ezek
együtt jelentkezhetnek a szokásos mezon- és barionspektrumokkal.
A témakörről részletes összefoglaló munkát közölt
Klempt és Zaitsev [7]. Fontosabb megállapításaik a
következők.
Az f0(1370) J PC = 0++,
f0(1500) J PC = 0++ és
f0(1710)
JPC = 0++ mezonokban megjelenhet skalár
gluonlabda komponens. Ez azonban széles háttérben van elkenődve.
Minden skalármezonban van 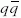 és
és
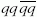 komponens. A
komponens. A 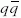 természetüket az
előállítás jelzi,
míg a bomlásuk és tömegük lényeges
természetüket az
előállítás jelzi,
míg a bomlásuk és tömegük lényeges 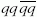 komponens
jelenlétére utal. Ámbár a rács-QCD számítások
a gluonlabda-állapotok egész spektrumát jósolják,
még az alapállapotot sem azonosították. Gluonlabda-
állapotok létezhetnek, de csak ≥1 GeV szélességgel.
komponens
jelenlétére utal. Ámbár a rács-QCD számítások
a gluonlabda-állapotok egész spektrumát jósolják,
még az alapállapotot sem azonosították. Gluonlabda-
állapotok létezhetnek, de csak ≥1 GeV szélességgel.
Hibrid állapotok előfordulhatnak egzotikus kvantumszámokkal
(amelyek a 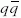 -mezonok számára nem
elérhetők), de lehetnek nem egzotikus kvantumszámaik
is. Hibrid jelöltek lehetnek a π2(1880) JPC = 2-+
és η2(1870) JPC = 2-+ rezonanciák, de
ehhez további megerősítés
szükséges. Hibrid állapotok létét a rács-QCD
számítások megjósolják, de jelenleg kísérleti adatok
nem sok jelét mutatják annak, hogy hibrid szabadsági
fok létezik a mezonspektroszkópiában. Igaz, létezésüket
sem tudják cáfolni.
-mezonok számára nem
elérhetők), de lehetnek nem egzotikus kvantumszámaik
is. Hibrid jelöltek lehetnek a π2(1880) JPC = 2-+
és η2(1870) JPC = 2-+ rezonanciák, de
ehhez további megerősítés
szükséges. Hibrid állapotok létét a rács-QCD
számítások megjósolják, de jelenleg kísérleti adatok
nem sok jelét mutatják annak, hogy hibrid szabadsági
fok létezik a mezonspektroszkópiában. Igaz, létezésüket
sem tudják cáfolni.
A multikvark állapotok létével kapcsolatban még
nincs egyértelmű bizonyíték. Egyes mezonok, például
az a0(980), f0(980),
 molekulajellegűek, de a
kísérleti tények kizárnak erősen kötött tetrakvark
(
molekulajellegűek, de a
kísérleti tények kizárnak erősen kötött tetrakvark
(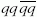 ) konfigurációt. Nagy
távolságoknál négy kvark
színsemleges objektumra válik szét. A rács-QCD számítások
nem mutatnak arra, hogy skalár mezonokban
a tetrakvark-konfigurációnak nagy szerepe lenne.
) konfigurációt. Nagy
távolságoknál négy kvark
színsemleges objektumra válik szét. A rács-QCD számítások
nem mutatnak arra, hogy skalár mezonokban
a tetrakvark-konfigurációnak nagy szerepe lenne.
Diakonov és munkatársai királismodell-számítások
alapján megjósolták egy egzotikus izoskalár barion
létét, amelynek spin-paritása 1/2+ és ritkasága S? = +1.
E θ+(1540)-nel jelölt "pentakvarkhoz" hozzárendelt
konfiguráció 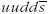 , ami nK+
(azaz
, ami nK+
(azaz 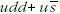 ) vagy
pK0 (azaz
) vagy
pK0 (azaz 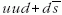 )
rezonanciaként jelentkezik. Az
állapot létét több laboratóriumban is kísérletileg észlelték,
de a vizsgálatok további megerősítésre szorulnak.
2009-ben üzembe lépett Japánban a J-PARC protonszinkrotron.
Ennek nagyteljesítményű protonnyalábja
lehetővé teszi a kaonok és pionok intenzív
előállítását, ez az első valódi kaongyár. A θ+ pentakvark
kutatását π-/K-reakciókban egyik első feladatuknak
tekintik.
)
rezonanciaként jelentkezik. Az
állapot létét több laboratóriumban is kísérletileg észlelték,
de a vizsgálatok további megerősítésre szorulnak.
2009-ben üzembe lépett Japánban a J-PARC protonszinkrotron.
Ennek nagyteljesítményű protonnyalábja
lehetővé teszi a kaonok és pionok intenzív
előállítását, ez az első valódi kaongyár. A θ+ pentakvark
kutatását π-/K-reakciókban egyik első feladatuknak
tekintik.
Nemrégiben a charmónium gerjesztési nívórendszerében
is találtak olyan nívókat, amelyek hadronmolekulákhoz
tartozhatnak (Wiedner [14]). Az új állapotok
természetének pontos meghatározása azonban
a jövő feladata.
A QCD egyik misztériuma, hogy eddig miért csak
kvark-antikvark és háromkvark-
állapotokat tudtak
biztosan azonosítani.
A hadronok
kölcsönhatásai
Az intenzív kutatások eredményeként
a hadronok kölcsönhatásait
egyre pontosabban
sikerül megismerni.
Különösen a pionok közötti
kölcsönhatás felderítésében
születtek látványos eredmények:
ma már az S-hullámú
ππ ütközési hosszat (ami a
kéttest-ütközések egyik fontos
paramétere) 2%-os pontossággal
ismerjük. Az eredményt
a rács-QCD, valamint
effektív térelméleti számításokkal
értelmezni is lehet.
Vizsgálták továbbá a rugalmas
πK-szórást, amiben
már a ritka kvark is szerephez
jut.
A mezon-mezon kölcsönhatások
vizsgálata –
kombinálva megfelelő mezontérelméleti
vagy királis
perturbációs elméleti számításokkal
– egyre inkább
a precíziós szakaszba lép.
Figyelemre méltó eredményeket értek el a πN és más
mezon-barion kölcsönhatások vizsgálatában is, főleg az
S-hullámú ütközési hossz meghatározásában. Mindezek
fontosak az atommagokat és hiperonokat összetartó erős
kölcsönhatások megismerése szempontjából.
Összegzés, kitekintés
A kvarkok 1960-as években történt felfedezése óta a
hadronfizika hatalmas fejlődésen ment át. A hadronok
szerkezetére, gerjesztett állapotaira, bomlásmódjaira,
kölcsönhatásaira rengeteg kísérleti adat gyűlt össze,
és ma már hatékony kvarkmodellek állnak rendelkezésre
a mezonok és barionok sajátságainak leírására.
A kezdetektől kiinduló (ab initio) rács-QCD számításokkal
a hadronok tömegét, egyes gerjesztett állapotait
és bomlásait is le lehet írni. A hadronok kölcsönhatásainak
vizsgálata precíziós szakaszba lépett.
A nyilvánvaló sikerek ellenére egyik tárgyalt témakör
sem tekinthető lezártnak. A hadronok szerkezetét
tovább szükséges vizsgálni az elérhető legnagyobb
energiáknál pp- és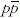 -reakciókból.
A "spinkrízis" sem
feloldott, új adatokra van szükség különösen leptonokkal
létrehozott, mélyen rugalmatlan szórási folyamatokból
és az általánosított partoneloszlási reakciókból.
Az összetevő kvarkokra alapozott kvarkmodellek
jó nyomon járnak a hadrongerjesztések és bomlások
leírásában. Már megjelentek következetesen relativisztikus
kvarkmodellek is. Ugyanakkor – különösen
a bomlások leírásában – néha nagy eltérések vannak
a kísérleti és elméleti eredmények között. A rács-QCD
számítások reményteljesek, de egyelőre a kísérleti
hadrontömegekhez illesztett kvarktömegekkel számolnak,
amik sokkal nagyobbak a fizikai (csupasz)
kvarktömegeknél.
-reakciókból.
A "spinkrízis" sem
feloldott, új adatokra van szükség különösen leptonokkal
létrehozott, mélyen rugalmatlan szórási folyamatokból
és az általánosított partoneloszlási reakciókból.
Az összetevő kvarkokra alapozott kvarkmodellek
jó nyomon járnak a hadrongerjesztések és bomlások
leírásában. Már megjelentek következetesen relativisztikus
kvarkmodellek is. Ugyanakkor – különösen
a bomlások leírásában – néha nagy eltérések vannak
a kísérleti és elméleti eredmények között. A rács-QCD
számítások reményteljesek, de egyelőre a kísérleti
hadrontömegekhez illesztett kvarktömegekkel számolnak,
amik sokkal nagyobbak a fizikai (csupasz)
kvarktömegeknél.
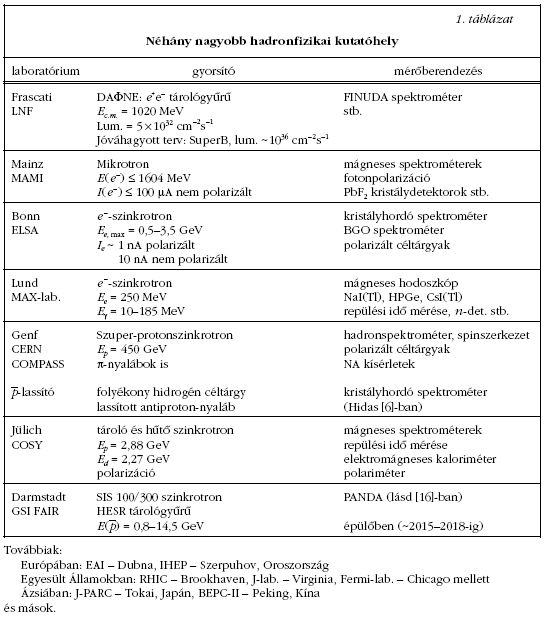
A vizsgálatok tovább folytatódnak. Az 1. táblázat
áttekintést ad néhány nagyobb hadronfizikai kutatólaboratóriumról,
valamint a gyorsító és mérőberendezéseikről.
Európában különösen reményteljes a GSI
FAIR PANDA programja. Ebben a nagy energiájú antiproton-
nyaláb, valamint a rendkívül fejlett mérőrendszer
(időprojekciós kamra, mikrovertex-detektorok,
driftkamrák, repülési időt mérő berendezés, elektromágneses
és hadron kaloriméterek, Cserenkov-detektorok,
eltérítő mágnesek, müonszámláló stb.) ideális
feltételeket teremtenek a hadronfizikai kutatásokhoz.
Jelentős előrelépés várható a Frascati LNF SuperB
programjának realizálásától is, ami a gyorsító luminozitásának
több mint három nagyságrenddel való emelését
tűzte ki célul. Japánban már működik a J-PARC
első valódi kaongyár. Az USA-ban a RHIC, Brookhaven
és a J-lab., Virginia programok jelentős hozzájárulást
adhatnak a hadronfizikához.
A hadronfizikai kutatások fejlődési irányait igen
részletesen tárgyalja A magfizika perspektívái Európában
című munka [15].
Irodalom
- Particle Data Group, Review of Particle Physics, J. Phys. G 37
(2010) 075 021.
- M. M. Islam, R. J. Luddy, A. V. Prokudin, Int. J. Mod. Phys. A 21
(2006) 1.
- B. Bressan, V. Greco, CERN Courier 49 (2009/September) 19.
- F. Bradamanti, Nucl. Phys. News 18/4 (2008) 32.
- S. D. Bass: The spin structure of proton. Rev. Mod. Phys. 77
(2005) 1257.
- P. Hidas, Fizikai Szemle 53/10 (2003) 359.
- E. Klempt, A. Zaitsev, Phys. Rep. 454 (2007) 1.
- T. Fényes: Részecskék és kölcsönhatásaik. Debreceni Egyetemi
Kiadó, Debrecen, 2007.
- S. Godfrey, N. Isgur, Phys. Rev. D 32 (1985) 189.
- S. Capstick, W. Roberts, Prog. Part. Phys. 45 (2000) 241.
- L. Ya. Glozman, Phys. Rep. 444 (2007) 1.
- I. Montvay, G. Münster: Quantum fields on a lattice. Cambridge
Univ. Press, Cambridge 1994.
- Ch. Davies, CERN Courier (2004/June) 23.
- U. Wiedner, Nucl. Phys. News 20/4 (2010) 19.
- G. Rosner, M. Makarow (eds.): NuPECC Long Range Plan 2010:
Perspectives of Nuclear Physics in Europe. European Science
Foundation, Strasbourg
- K.-T. Brinkmann, P. Gianotti, I. Lehman, Nucl. Phys. News 16/1
(2006) 15
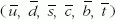 létezik, a hadronok sokféle
kombinációban épülnek fel. Az azonos (vagy nagyon
hasonló) kvarkösszetételű mezonoknak gyakran
külön nevet is adtak. Így 2010-ben már több, mint 150
mezon- és több, mint 130 barionállapot volt ismeretes.
A hadronokat tömegeikkel, összetételükkel és
különböző kvantumszámaikkal lehet jellemezni. Illusztrációként
az 1. ábrán fel van tüntetve néhány
mezon- és barionállapot az Iz izospinvetület-, S? ritkaság-
és C? bájkvantumszám-térben a kvarkösszetételükkel
együtt. Teljesebb áttekintés található a Particle
Data Group [1] közleményben.
létezik, a hadronok sokféle
kombinációban épülnek fel. Az azonos (vagy nagyon
hasonló) kvarkösszetételű mezonoknak gyakran
külön nevet is adtak. Így 2010-ben már több, mint 150
mezon- és több, mint 130 barionállapot volt ismeretes.
A hadronokat tömegeikkel, összetételükkel és
különböző kvantumszámaikkal lehet jellemezni. Illusztrációként
az 1. ábrán fel van tüntetve néhány
mezon- és barionállapot az Iz izospinvetület-, S? ritkaság-
és C? bájkvantumszám-térben a kvarkösszetételükkel
együtt. Teljesebb áttekintés található a Particle
Data Group [1] közleményben.
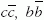 ) sajátságaiból,
valamint a szóráskísérletekből
ismerhetők meg. A helyzet hasonló a
magfizika őskorához, amikor az atommagot összetartó
erők felderítése céljából az egy protont és egy
neutront tartalmazó deuteron sajátságait kezdték tanulmányozni.
) sajátságaiból,
valamint a szóráskísérletekből
ismerhetők meg. A helyzet hasonló a
magfizika őskorához, amikor az atommagot összetartó
erők felderítése céljából az egy protont és egy
neutront tartalmazó deuteron sajátságait kezdték tanulmányozni.
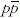 rugalmas szórás,
rugalmas szórás,
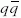 -kondenzátum (pionfelhő) hat kölcsön a
másik proton hasonló rétegével, ami diffraktív szóráshoz
vezet. Kis |t| tartományban (0 és 1 GeV2 között)
pp-szórásnál a Coulomb- és erős kölcsönhatások között
interferencia lép fel.
-kondenzátum (pionfelhő) hat kölcsön a
másik proton hasonló rétegével, ami diffraktív szóráshoz
vezet. Kis |t| tartományban (0 és 1 GeV2 között)
pp-szórásnál a Coulomb- és erős kölcsönhatások között
interferencia lép fel.


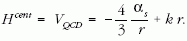

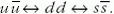 .
.
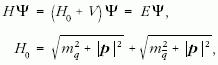
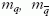 , a kvark, illetve antikvark nyugalmi
tömege, p a relatív impulzus tömegközépponti rendszerben,
, a kvark, illetve antikvark nyugalmi
tömege, p a relatív impulzus tömegközépponti rendszerben,
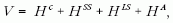
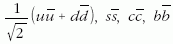
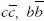 és más c- és b-kvark
tartalmú mezonokra
is vannak adatok. Számítottak továbbá parciális
bomlási szélességeket (például a ρ → ππ, φ → KK K* →
Kπ bomlásokra) és sok más mennyiséget is.
és más c- és b-kvark
tartalmú mezonokra
is vannak adatok. Számítottak továbbá parciális
bomlási szélességeket (például a ρ → ππ, φ → KK K* →
Kπ bomlásokra) és sok más mennyiséget is.
 )
mezonoktól
a könnyű pionokig. Az alacsonyan fekvő állapotok
energiáit elég jól leírja. A modell hátránya, hogy a
relativisztikus effektusokat csak félig kvantitatíven
veszi figyelembe (a Hamilton-operátor kimutathatóan
nem kovariáns), továbbá hogy gluonlabdákat és hibrid
állapotokat nem tartalmaz. Ez utóbbiak tárgyalására
a rács-QCD számításoknál visszatérünk.
)
mezonoktól
a könnyű pionokig. Az alacsonyan fekvő állapotok
energiáit elég jól leírja. A modell hátránya, hogy a
relativisztikus effektusokat csak félig kvantitatíven
veszi figyelembe (a Hamilton-operátor kimutathatóan
nem kovariáns), továbbá hogy gluonlabdákat és hibrid
állapotokat nem tartalmaz. Ez utóbbiak tárgyalására
a rács-QCD számításoknál visszatérünk.

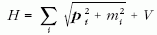
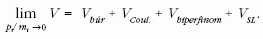


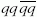 vagy
vagy
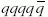 multikvarkállapotok is, és ezek
együtt jelentkezhetnek a szokásos mezon- és barionspektrumokkal.
multikvarkállapotok is, és ezek
együtt jelentkezhetnek a szokásos mezon- és barionspektrumokkal.
 molekulajellegűek, de a
kísérleti tények kizárnak erősen kötött tetrakvark
(
molekulajellegűek, de a
kísérleti tények kizárnak erősen kötött tetrakvark
(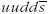 , ami nK+
(azaz
, ami nK+
(azaz 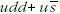 ) vagy
pK0 (azaz
) vagy
pK0 (azaz 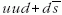 )
rezonanciaként jelentkezik. Az
állapot létét több laboratóriumban is kísérletileg észlelték,
de a vizsgálatok további megerősítésre szorulnak.
2009-ben üzembe lépett Japánban a J-PARC protonszinkrotron.
Ennek nagyteljesítményű protonnyalábja
lehetővé teszi a kaonok és pionok intenzív
előállítását, ez az első valódi kaongyár. A θ+ pentakvark
kutatását π-/K-reakciókban egyik első feladatuknak
tekintik.
)
rezonanciaként jelentkezik. Az
állapot létét több laboratóriumban is kísérletileg észlelték,
de a vizsgálatok további megerősítésre szorulnak.
2009-ben üzembe lépett Japánban a J-PARC protonszinkrotron.
Ennek nagyteljesítményű protonnyalábja
lehetővé teszi a kaonok és pionok intenzív
előállítását, ez az első valódi kaongyár. A θ+ pentakvark
kutatását π-/K-reakciókban egyik első feladatuknak
tekintik.
