
Fizikai Szemle honlap |
Tartalomjegyzék |
Teiermayer Attila
Karolina Gimnázium, Szeged
A fényt kibocsátó dióda (Light Emitting Diode = LED) működésének fizikája nem része a középiskolai törzsanyagnak, legfeljebb fakultációs órákon vagy szakkörön tárgyalható. A LED-ek mint sajátos fényforrások azonban jól felhasználhatók a fizikatanítás számos területén. Alkalmazásuk több szempontból is előnyös: egyrészt könnyen és olcsón beszerezhetők, használatuk nem igényel speciális felszerelést, és lehetőséget nyújtanak arra is, hogy érdeklődőbb, tehetségesebb diákjaink otthon is kísérletezzenek velük; másrészt az elvégzett kísérletekhez, mérésekhez számítási feladatokat is kapcsolhatunk. A kísérletek magyarázatot, értelmezést kívánnak, ezek során sokat taníthatunk meg diákjainknak a félvezető-fizika speciális területeiről is.
Írásomban a LED-ek néhány iskolai alkalmazását szeretném bemutatni a teljesség igénye nélkül.
Egyetlen LED fényereje csekély, ha azonban egy foglalatban sok LED helyezkedik el, az együttes fényerő összemérhető a hagyományos lámpákéval, miközben elektromos energiaigénye sokkal kisebb azokénál. A kereskedelemben bő választékban kaphatók ilyen hálózati feszültségre készült LED-es fényforrások. A LED működtetésére néhány volt egyenfeszültség szükséges. A sok LED-ből álló lámpák foglalatába beépített elektronika biztosítja, hogy a diódák a 230 V-os hálózati feszültségről táplálva is működtethetők legyenek.
A 2010. májusi emelt szintű érettségi vizsga szóbeli tételsorának egyik mérési feladata az volt, hogy a vizsgázó hasonlítsa össze egy hagyományos izzó és egy geometriailag teljesen hasonló felépítésű kompakt fénycsöves fényforrás relatív fényteljesítményét zsírfoltos fotométer segítségével. Relatív fényteljesítményen a kitűzött feladat a fényforrás fényteljesítménye és a felvett elektromos teljesítmény hányadosát, tehát a fényhasznosítást értette. Ez a feladat továbbfejleszthető úgy, hogy a másik széles körben elterjedt modern fényforrással, a LED-es fényforrással történjen az összehasonlítás, vagy a két új típusú fényforrás relatív fényteljesítménye kerüljön összevetésre.
Ehhez a mérési feladathoz rövid, de tanulságos számítási feladatokat kapcsolhatunk. E témakör feldolgozása történhet szakköri keretek között, tanórán csoportmunkában, vagy frontális foglalkozásban.
A Bunsen által kifejlesztett zsírfoltos fotométer egyszerűen használható a mérés elvégzéséhez. Ha a zsírfoltot csak egy irányból világítjuk meg, a fényforrás felőli oldalon a folt sötétebb, a szemközti oldalon pedig világosabb, mert a zsírfolt fényáteresztő képessége nagyobb, mint az őt tartalmazó papíré. Ha az 1. ábrán látható módon mindkét oldalról megvilágítjuk a fényfoltot, és megtaláljuk a papírlap azon helyzetét, ahol a folt mindkét oldalon azonos fényességű, akkor a folt megvilágítottsága megegyezik [1].
Szakirodalmakból [2] megtudhatjuk, hogy a folton a fényforrás fényteljesítménye egyenesen arányos a folt és a fényforrás távolságának négyzetével, így
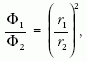
illetve azt, hogy a fényhasznosítások aránya az
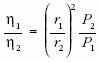
összefüggéssel számolható ki, ahol Φ a fényforrás fényteljesítményét, η a fényhasznosítást, r a folt és fényforrás távolságát, P a fényforrás elektromos teljesítményét jelenti.
Méréseimhez egy 60 W-os hagyományos izzót, egy MEGAMAN Party Color típusú kompakt fénycsövet (gömb alakú búra, átmérő: 6 cm, teljesítmény: 6 W, élettartam 10 000 óra), és egy FORlight típusú, 60 LED-et tartalmazó fényforrást (gömb alakú búra, átmérő: 5,7 cm, teljesítmény: 3 W, élettartam 50 000 óra) használtam. A fényforrások kiválasztásánál figyeltem arra is, hogy mindegyik fénye "meleg" legyen.
Első feladatként adhatjuk diákjainknak, hogy méréssel hasonlítsák össze a hagyományos fényforrás és a két modern fényforrás fényteljesítményét, fényhasznosítását, és ezen adatokból jósolják meg a két modern fényforrás fényhasznosításának arányát, majd méréssel ellenőrizzék a számítás eredményét.
Először tehát összehasonlíthatjuk a hagyományos izzót a kompakt fénycsövessel és a LED-es fényforrással. A méréseket a fent leírtak alapján elvégezve kapjuk, hogy:
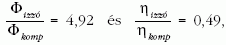
valamint
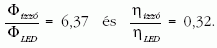
A méréseket elvégezve jóslatként
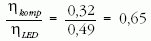
értéket kapunk. Ha ezután a két modern fényforrással a mérést elvégezzük, ez a hányados 0,71-nek adódik. Ha a mért és a számolt eredmény viszonylag közel esik egymáshoz, az eredménnyel elégedettek lehetünk, hiszen a foltok világosságának vagy sötétségének megítélése szubjektív, ezért itt a relatív fényteljesítmények arányának becsléséről lehet csupán szó.
A most következő feladatok elméleti jellegűek, de az energiatakarékosságra nevelés szempontjából fontosak lehetnek.
Az előző mérési eredmények után a számítást elvégezve a LED-es fényforrással 50 000 óra alatt körülbelül 49 000 Ft-ot fizetünk az áramért, a kompakt fénycsöves fényforrással körülbelül 85 000 Ft-ot, (a 14 W-os kompakt fénycsőnél körülbelül 40 000 Ft-ot) a hagyományos izzóval pedig 154 000 Ft-ot. (50 darab hagyományos izzó ára 4500 Ft, 5 kompakt fénycsőé 9500 Ft, míg a LED-es fényforrásé 3800 Ft, ez a különbség az áramfogyasztáshoz képest elhanyagolható.)
A számok alapján egyértelműen a LED-es fényforrás mellett érdemes döntenünk. Ugyanakkor az is az igazsághoz tartozik, hogy napi 8 óra üzemidővel számolva az 50 000 óra körülbelül 20 év, és az emberek világítás szempontjából ekkora távlatban nem szoktak tervezni, kiindulva abból, hogy 20 évvel ezelőtt a mai újdonságokra nem számíthattak volna.
Ezek a feladatok segíthetnek minket abban, hogy diákjainkat a meglévő energiával való takarékoskodásra neveljük, élményt jelenthet eközben az, hogy egy általunk elvégzett órai mérés szolgáltatja a számítási feladat alapját.
Mint minden diódán, a LED-en is csak egy irányban haladhat át az áram. Ez teszi lehetővé, hogy könnyen, egyszerűen készítsünk belőle stroboszkópot. Váltakozó feszültségre kapcsolva a LED csak félperiódusonként világít. 50 Hz-es frekvencián ez nem érzékelhető, ha azonban a frekvenciát csökkentjük, a jelenség jól megfigyelhető.
Az 2. ábrán látható stroboszkópot egy LED-es zseblámpából készítettük. A zseblámpa 20 kis fényerejű LED-ből áll, és eredetileg 4,5 V egyenfeszültségről működtethető. Kis átalakítással azonban elérhető, hogy hanggenerátorra csatlakoztathassuk. A lámpában a LED-es hálózat egyik kivezetése maga a fémtest, a másik pedig a csőben közvetlenül a LED-ek alatt található kis rugó.
A cső falát szakkörös diákjaimmal két helyen átfúrtuk, egy vezetéket a cső belső falára forrasztottunk, egy másikat pedig egy szigetelőszalaggal bevont krokodilcsipesz segítségével a rugóhoz rögzítettük. A vezetékeket banánhüvelyen keresztül köthetjük a hanggenerátorra. Figyelnünk kell arra, hogy a váltófeszültség alkalmazásakor a hanggenerátor által kiadott effektív feszültség nem lehet nagyobb, mint
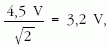
hiszen a LED-es hálózaton eső csúcsfeszültség legfeljebb 4,5 V lehet! A lámpa által felvett teljesítmény a mérések szerint 400 mW körül van.
A hanggenerátorról működtetett diódák villogó megvilágításában a folyamatos mozgások szakaszosnak tűnnek, a stroboszkóphatás jól megfigyelhető. Ha a mozgó test fényvisszaverő-képessége jó, például fehérre van festve, a helyiséget elsötétítve és a mozgó test mögé sötét hátteret helyezve, egyszerű stroboszkópunk megvilágítása mellett "strobo-képeket" fotózhatunk.
A különböző színű fény hullámhosszának mérése fontos optikai kísérlet. Egyetemi laboratóriumokban drága spektroszkópokkal speciális töltésű gázkisülési csövek fényét vizsgálják. Középiskolai szinten jól megfelel a különböző színű LED-ek fényének vizsgálata egyszerű optikai rácson keresztül. A hullámhosszmérést szubjektív észleléssel vagy egyszerű digitális kamerával (például mobiltelefon kamerája) készített fotó segítségével végezhetjük el.
Színes LED mellé helyezzünk cm-skálát (fehér papír-mérőszalagot vagy vonalzót)! A LED-et igazítsuk például a 10 cm-es osztásvonalához! Távolodjunk el a LED-től előzőleg kimért 1-2 méter távolságra, majd nézzünk a világító LED-re úgy, hogy közvetlenül egyik szemünk elé optikai rácsot tartunk! Ha a rács osztásvonalai függőlegesen állnak, a 3. ábrához hasonló képet látunk. Középen, a skála kiválasztott vonalánál a világító LED, jobbra és balra szimmetrikusan a két elsőrendű elhajlási maximum található. Ez a mérés szubjektív észlelésen alapuló módja.
Ha mindkét szemünkkel egyszerre nézünk, a természetes látványt és a rácson keresztül látott képet agyunk egymásra vetíti. Így jól meg tudjuk állapítani, hogy a diódától jobbra és balra eső elhajlási maximumok a centiméterskálán hová esnek. A rács és a LED távolságát (L), az elhajlási maximumok skálán mért távolságát (x) és az optikai rács rácsállandóját (d) ismerve a fény hullámhossza meghatározható (4. ábra).
A szubjektív látványt rögzíthetjük digitális fényképezőgéppel (például mobiltelefon kamerájával). A fényképezőgépet szembe állítjuk a centiméterskála fölött lévő diódával, közvetlenül az objektív elé tartjuk az ismert rácsállandójú optikai rácsot, és exponálunk. Ezután lemérjük és feljegyezzük a LED és az optikai rács (illetve a gép lencséje) közti távolságot. A kamera a szemünkhöz hasonlóan alkot képet a látványról. A rögzített digitális kép azonban a rácsállandó értékével, valamint a kamera és tárgy helyszínen lemért távolságával kiegészítve a mérés maradandó dokumentuma. A fotót a kísérlettől függetlenül utólag bárhol, bármikor megnézhetjük és kiértékelhetjük.
Az 3. ábrán látható kép készítésekor a mobiltelefon lencséje L = 29,5 cm távol volt a diódától, az optikai rács 300 vonalat tartalmazott milliméterenként (rácsállandó d = 1/300 mm). A képen a skála csekély elmosódottsága ellenére jól megbecsülhető a két oldalsó elhajlási maximum távolsága, ennek fele a számításhoz szükséges x érték, ez alapján x ≈ 5,3 cm.
Az így ismert adatokkal és a fenti összefüggésekkel számolva a LED sárga fényének hullámhossza kerekítve
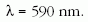
A tapasztalatok szerint az elhajlási kép leírt fotózása után a legkülönfélébb színes LED-ek hullámhosszát a diákok otthoni munkában is meg tudják határozni. A fotó kiértékelése feleltetéshez is kapcsolható és dolgozatban is feladható.
Mint minden fizikai mérésnél, az előbb leírt hullámhosszmérésnél is meg kell adnunk a mérés pontosságát. A LED és a rács távolságánál a leolvasási pontosság 0,5 cm-nek vehető, a képről a folt leolvasását 2-3 mm-es hibával tehetjük meg. Ebből 10%-os nagyságrendű hiba származhat. Ugyanakkor ennél a mérésnél nem is a pontos számérték a fontos, hanem az, hogy egy igen kicsiny mennyiséget a legtöbb középiskolában fellelhető egyszerű eszközök segítségével viszonylag nagy pontossággal meg tudunk határozni. Különösen igaz ez a következő részben említendő infravörös fényre.
Az elektromágneses spektrum infravörös tartományát szemünk nem érzékeli. Egyszerűen bemutatható ez például a tv-készülék távvezérlőjével. Az eszköz előlapján infravörösben sugárzó LED található. Szabad szemmel nem látjuk, hogy a LED a távirányító gombjainak lenyomásakor fényt bocsátana ki. A digitális fényképezőgép azonban ezt a fényt is "látja". A kamera chipje érzékeli az infravörös sugárzást és meg is jeleníti a folyadékkristályos képernyőjén. Ha a távirányító gombjait lenyomjuk, a képernyőn úgy látjuk, hogy a LED világít. A digitális kamerák e tulajdonságát felhasználhatjuk arra, hogy optikai rács segítségével megmérjük a szemünk számára láthatatlan fény hullámhosszát.
Az eljárás hasonló, mint a színes LED hullámhosszának kamerával való mérésénél. A különbség abban van, hogy most az elhajlási maximumok kis intenzitása miatt sötétben kell fényképet készíteni, így a képre nem fotózhatunk skálát. A probléma kettős fotózással oldható meg. Készítsünk fényképet először világosban, ekkor például a távirányító szélessége lehet a viszonyítási alap (természetesen ekkor a helyszínen le kell mérni és fel kell jegyezni az eszköz valódi szélességét). A fotózást ezután a távirányító működése közben, az optikai rácsot közvetlenül a kamera lencséje elé tartva meg kell ismételni. Ügyeljünk arra, hogy a kamera és a infra-LED távolságát le kell mérnünk, és ez a távolság a két fénykép készítése során meg kell egyezzen. Ha a távirányító szélességét mérjük le, akkor a rácsot úgy helyezzük a kamera elé, hogy az elhajlás függőlegesen történjen, hiszen ilyenkor a vízszintes méretek nem torzulnak.

|

|
Az 5. és a 6. ábra így készített két felvételt mutat. Így a távirányító valódi 4,3 cm szélességéből arányosan kiszámolhatjuk a már említett x távolságot. A felvétel készítésekor a lencse és a LED távolsága L = 25 cm volt, a rácsállandó pedig d = 1/300 mm. Az eredeti fotó alapján x = 7 cm, a számítást elvégezve az infravörös fény hullámhosszára 899 nm-t kapunk.
A leírt kettős fotózás feleslegessé válik, ha találunk olyan távirányítót, ami két infravörös LED-del működik (7. ábra). Ilyenkor elegendő egyetlen fotót készíteni az elhajlásról. Arra kell csak figyelnünk, hogy az optikai rács vonalai párhuzamosak legyenek a két LED által meghatározott egyenessel. Ilyen felvétel látható a 8. ábrán.
A távirányítón vízszintesen egymás mellett helyezkedik el a két LED, a kamera elé tartott optikai rács vonalai ennek megfelelően vízszintesen álltak. Fényelhajlás a rács vonalainak irányára merőlegesen lép fel, ezért a két LED távolságát az elhajlás nem változtatja meg. Az elhajlási maximumok távolságát és a LED-ek távolságát a fotón mérjük. Az elhajlási maximumok valódi távolságát a fotó léptékének ismeretében tudjuk meghatározni. Ehhez a LED-ek fotón mért távolságát és a LED-ek távirányítón lemért távolságát használhatjuk fel.
A 8. ábrán az elhajlási kép látható. A valóságban a két LED távolsága 8 mm volt, a felvétel készítésekor a távirányító a kamerától L = 16 cm távolságban helyezkedett el, a rácsállandó d = 1/200 mm. A mérést és a számítást elvégezve a hullámhosszra 941 nm-t kapunk.

|

|
A fent leírt kísérletek csak egy szeletét adják a LED-ek középiskolai alkalmazásának. A világító diódák használatán keresztül taníthatunk anyagszerkezeti ismereteket, fizikai optikát, ezen kívül megmérhetjük a Planck-állandót [3], és beszélhetünk diákjainknak az energiatakarékosságról, a jövő (vagy már a jelen) fényforrásairól.
A kísérletek nemcsak színesíthetik a tanórát vagy a szakköri foglalkozást, hanem lehetőség nyílik mérések végzésére, kiértékelésére, és ehhez kapcsolódóan számítási feladatok megoldására.
Diákjaink így nemcsak az órán találkozhatnak a LEDekkel, hanem otthon is kísérletezhetnek, ezzel látens módon megnövelhetjük a fizika tantárgy heti óraszámát.
___________________________