Fizikai Szemle honlap |
Tartalomjegyzék |
Abonyi Iván
ELTE TTK
Kármán Tódor (1881. május 11. Budapest – 1963. május 7. Aachen) a magyarországi mérnökgenerációk egyik legkiválóbb képviselője, sokoldalú fizikus és gépészmérnök, zseniális szervező-egyéniség, Neumann János szerint a tudományos tanácsadó (scientific consultant) szerepkörének egyik kimagasló személyisége volt.
Középiskolai tanulmányait a Trefort-féle Mintagimnáziumban végezte. Ezt az iskolatípust édesapja, Kármán Mór tervezte meg, hogy a leendő középiskolai tanárok itt gyakorolva szerezhessék meg a pályájuk során szükséges pedagógiai ismereteket az egyetemi tanulmányaik mellett. Az iskolatípust Trefort Ágoston (1817– 1888) közoktatási minisztersége alatt valósították meg. Ez lett – röviden szólva – a "Minta" gimnázium.
A Kármán-család a Minta közelében, attól alig két háztömbnyire, a Szentkirályi utcában lakott. Tódor utolsó gimnáziumi évei során az Eötvös Loránd indította tanulmányi versenyeken számos jó helyezést ért el. Itt érettségizett, majd a budapesti Műegyetemre ment, amit akkor még Királyi József Műegyetemnek neveztek. Gépészmérnöknek készült.
Tanulmányait sikeresen végezte, oklevelét 1902-ben szerezte meg. Nagy hatással volt rá Bánki Donát (1859–1922), aki végzése után tanársegédként alkalmazta, de ugyanakkor Ganz Ábrahám vagongyárába is elküldte.
Munkahelyén a nyomott rudak kihajlásának problémáival foglalkozott. Ez a problémakör nagy részben elkísérte későbbi pályáján, hiszen ezek a szerkezeti anyagok a legkülönfélébb műszaki konstrukciókban fontos szerepet játszanak. Például hidak és más építmények esetében, de döntő mértékben az éppen akkortájt induló repülőgépipar területén tűntek ki fontosságukkal.
1906-ban Kármán a Magyar Tudományos Akadémia ösztöndíjat elnyerve Göttingenbe jutott, Ludwig Prandtl (1875–1953) tanszékére. Ez a körülmény döntő hatással volt tudományos pályájára – ekkor jegyezkedett el a repülés, a különböző repülő szerkezetek problémáival és szépségével. Ez volt az az időszak Prandtl életében is, amikor nyilvánvalóvá vált, hogy a repülés nem egyszerűen úszás a levegőben (mint egy arkhimédészi probléma), mert az igazi feladat az lenne, hogy a levegőnél nehezebb testek is repülhessenek. Világossá vált, hogy nem elég az Arkhimédészféle sztatikus felhajtóerő a repüléshez, hanem egy dinamikai erőhatás is szükséges. Ennek szoros kapcsolata van mind a repülő szerkezet szárnyának alakjával, mind a már mozgó szerkezet körül kialakuló áramlással. Az is kiderült már akkor, hogy a repülő test elemei által keltett hatások is befolyásolják a dinamikai felhajtóerőt. Akármilyen kényelmes a levegőt ideális közegnek tekinteni, mégsem lehet elhanyagolni a test és a közvetlenül hozzáérő levegő kölcsönhatását, a dinamikus határréteget. Ez az éppen születő problémakör természetesen megragadta a fiatal Kármán Tódor fantáziáját.
De előbb a megkezdett feladat megoldása volt soron. 1909-ben a nyomott rudak kihajlásáról készített tanulmánya alapján a Göttingeni Egyetem doktorrá fogadta és magántanárrá habilitálta.
Ezután már sor kerülhetett az örvénysorok és a közegellenállás kapcsolatának vizsgálatára.
Az örvénysorok kérdése tulajdonképpen a hidrodinamika (esetünkben az aerodinamika) jellegzetes áramlástani problémája. A korábbi eredményes kutatók természetes ösztönnel a síkbeli áramlásokkal foglalkoztak. Ekkor hallgatólagosan felteszik, hogy a z-tengely irányában nem történik semmi, mondjuk, hogy ebben az irányban végtelen kiterjedésű a test, így minden érdekes dolog az x-y síkban játszódik le, tehát síkbeli áramlást vizsgálhatunk. Ebbe a síkbeli áramlásba helyezzünk el egy akadályt, amelyet az áramló folyadék vagy gáz körüláramol. Ha az akadály körlap, akkor az események leírása eleinte még nagyobb nehézségek nélkül elvégezhető. Ezért nem csodálatos, hogy a síkbeli áramlás kör alakú akadály körül problémakör már a 18. században, majd a 19. században is – főleg azóta, hogy kialakult a komplex változójú függvények tanulmányozása, amiben a körnek centrális szerep jutott – úgyszólván menetrendszerűen napirenden volt. Ám megjelentek a fizikusok és mérnökök által felvetett kínos kérdések: az áramló ideális folyadék és az akadály vajon tapad-e egymáshoz, van-e és ha van, milyen a dinamikus határréteg? Ez a probléma a 19. század utolsó évtizedeiben vált igazán aktuálissá.
Közben úgy látszott, mintha a hidrodinamika tankönyvei csakúgy, mint a komplex függvénytani munkák egyszerűen leálltak volna, (átmenetileg) elégnek ítélték volna eredményeiket, amelyek igen jelentősek és igen hatásosak voltak. E hirtelen megállás nyomai látszanak a kor mechanikai tan- és kézikönyvein is. Az a benyomásunk, hogy hiányzott az új lökés, amely a repülés ügyének kibontakozásával érkezett meg a századfordulón.
Az új korszak képviselői Ludwig Prandtl, de legfőként Kármán Tódor. Prandtl kezdett foglakozni azzal, hogy mi történik a repülők szárnyprofilja körül a repülés közben, egyelőre természetesen kör keresztmetszetű szárnyprofilt vizsgálva. Ezt követhette az a remény, hogy a körkeresztmetszetet majd valaki ideális szárnyprofillá transzformálja, ha másképpen nem lehet (ideálisan zárt képletben), akkor legalábbis jó közelítésben.
Ebben a küzdelemben játszott rendkívül fontos szerepet Kármán Tódor. Eljárását a következő részben ismertetjük, csak előbb még néhány megjegyzést teszünk.
Az alábbiakban ismertetendő Kármán-féle eredmények 1911–12-ben láttak napvilágot. Ekkor jelent meg az első tanulmány Kármán tollából a Göttinger Nachrichten oldalain [1]. A cikk kimondott célkitűzése az volt, hogy áramlástanilag indokolja Osborne Reynolds közegellenállási képletét abban az esetben, amikor a körüláramlott test "hátsó része" nem gömbölyű, hanem szögletes, olyan mint egy konzervdoboz alja. Igen érdekes, hogy a számítások eredménye kétféle, lényegében mégis hasonló esetre vezet. Az akadály "hátsó" széleinél az áramlás "befelé" fordul, a két szélen örvénylő áramlás indul meg, majd leszakad az akadályról. Ezek az örvények energiát hordoznak, ez fogja az ellenállást okozni. Az örvények impulzusnyomatékot is képviselnek, az akadály szemben lévő rétegeinél ellenkező forgásirányuk miatt, a "jobbról", illetve "balról" bekanyarodó örvénygyűrűk egymással szemben forognak, az impulzusnyomatékuk összege (legalább időátlagban) zérus. A két ilyen örvénytípus között a különbség annyi, hogy az egyiknél az örvények pontosan (időben) párosával lépnek fel (és majd szakadnak le), míg a másiknál az örvények (kis időeltolódással) egymást szakaszosan követik. Ezért van az, hogy ebben az eseten az elvitt impulzusnyomaték csak időátlagban zérus összegű. A részletes tanulmányozásra kis idővel később, 1912-ben H. Rubach közreműködésével került sor, ez a tanulmány a Physikalische Zeitschrift hasábjain jelent meg [2].
Egy szó, mint száz, ez a két tanulmány kicsit több mint 100 éve jelent meg. A Göttinger Nachrichten akkoriban a szakmai "világirodalom" fontos orgánuma volt (többek között David Hilbert is ezen az egyetemen dolgozott). Ma már nem csodálkozhatunk azon, hogy ez a lap csak a nagyobb könyvtárak legmélyén, külön épületek "süllyesztőiben" található. De a Physikalische Zeitschrift – szerencsére – ma is azonnal hozzáférhető. Nem győzzük hangsúlyozni, hogy ez a lap, a Physikalische Zeitschrift, milyen jelentőségű, hiszen a korszak a fizika legkülönfélébb fejezeteinek 20. századi felfedezéseit mutatja be a kutatók első publikációin – és persze, esetleges vitacikkein – keresztül.
Most inkább a felett akarunk csodálkozni, hogy az örvényúttal kapcsolatos cikk(ek) és a témájuk (a múlt évtizedek során többször is megmutatkozó rendkívüli jelentősége ellenére) mennyi ideig várták, hogy a 20. század tankönyveiben méltó bemutatásuk megtörténjék.
Az a benyomásunk, hogy a tudományegyetemi használatra készült elméleti fizikai tankönyvek közül a legendás Arnold Sommerfeld-féle könyvsorozat az első, amelyben a szerző aránylag részletesen bemutatja az örvényes síkbeli áramlásokat a Kármán-féle eredményekig és hivatkozik a közegellenállás tárgyalásában Kármán korszakalkotó szerepére. De azért vegyük észre, hogy Arnold Sommerfeld (1868–1950), aki oly sok fiatal zsenit nevelt fel a fizika igazán nagynevű kutatójává (például Werner Heisenberg et és Wolfgang Paulit), és aki maga is tevékeny részt vett a modern atomfizika feltárásában [3], miközben sajtó alá rendezi A deformálható közegek mechanikája című tankönyvét [4] – az első kiadás 1944-ben, a negyedik kiadás már halála után, 1957-ben –, úgy teszi ezt, hogy az eredményeknek a súrlódási jelenségeken túlmenő, főleg a repülést érintő vonatkozásairól egyetlen sort sem ír!
Hazánkban a tudományegyetemi célokra készült tankönyvek közül – amelyek a II. világháborút követő megújulás során, 1950 után készültek – kiemelkedő jelentőségű volt Budó Ágoston Mechanika kötete [5] 1951-ből. Ebben a kötetben hiába keressük a Kármán-eredményeket. Ezekre a 3. kiadásig, 1969-ig kellett várni. Pedig akkor már nemcsak a szuperszonikus repülőgépek, hanem a tevékeny űrkutatás szintjére is eljutottunk.
A 20. század második felének legendás elméleti fizikai tankönyvsorozata a Nobel-díjas L. D. Landau és a Lenin-díjas E. M. Lifsic nevéhez fűződik. A Moszkvai Egyetemen tartott előadások nyomán készült kéziratokból indult ki a sorozat, Landau előadásait eleinte Lifsic rendezte sajtó alá. Az első kötet a mechanika általános megalapozását szolgálta. A második lett igazán legendás, a Klasszikus erőterek, a relativitáselmélet páratlanul jól sikerült áttekintésével igazán maradandó. A Hidrodinamika című kötet [6] mintegy 680 oldala óriási összefoglaló, azonban a Kármán-féle problémakör nem szerepel benne. (Kénytelenek vagyunk Kármán NATO-ban betöltött szerepére gondolni!)
Egy meglehetősen rövid – egyetlen oldalt is alig igénylő – említés található A mérnöki tudományok kézikönyve [7] H. Niedring cikkében, 1993-ban.
A legfrissebb magyar tankönyvirodalomban is találunk egy rövid utalást a Kármán-féle örvénysorra Demény András, Erostyák János, Szabó Gábor, Trócsányi Zoltán: Fizika I.: Klasszikus mechanika című könyvében [8]. Hasonlóképpen egy rövid fejezet végén szerepel egy utalás Kármán Tódor felfedezte örvényútra Bérces György, Erostyák János, Klebniczki József, Litz József, Pintér Ferenc, Raics Péter, Skrapits Lajos, Sükösd Csaba és Tasnádi Péter szerzők A fizika alapjai című tankönyvében [9].
Most röviden próbáljuk meg érzékeltetni, hogy Kármán Tódor szerint mi a közegben mozgó test által tapasztalt ellenállás mechanizmusa. Különösképpen azt vizsgáljuk meg, hogy az Osborne Reynolds-féle tapasztalati közegellenállási törvényt meg lehet-e magyarázni ezzel az örvényleválási mechanizmussal.
A cél tehát megadni a folyadékban U sebességgel haladó testre kifejtett közegellenállási erő képletét:
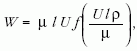
ahol
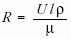
a Reynolds-szám, µ a ρ sűrűségű folyadék viszkozitása, l pedig egy aránylag tetszőlegesen választható, mégis jellegzetes hosszúság, amely az áramlási térbe merített testre jellemző, vagy legalább is az alakjától függ. A tapasztalat szerint az R a nagyon nagy viszkozitás, vagy a lassú mozgás esetén jó közelítéssel állandó. Az R = 0 határesetet a Stokes-féle közegellenállási képlet adja (f = 1), amely igen jó közelítéssel érvényes az "elég egyszerű" alakú testek (gömbök?) esetében, a tapasztalatok széles köre által alátámasztva. Az ellenkező határeset (R→ ∞) vonatkozhat éppenséggel a repülésre is, de mindenképpen külön megfontolást érdemel. Az idevágó tapasztalatok (már 100 évvel ezelőtt is!) – például a légcsavar gyors mozgására gondolva – azt mutatták, hogy az R a közegellenállástól már függetlenné válik. Ebből az szűrhető le, hogy az áramlási tér az akadály (a test) körül két részre bontható. Az egyik a közvetlen akadály körüli zóna. A közeli zóna folytonos változási tartomány, olyan mintha a testre nem is hatna közegellenállás. A másik pedig a távoli zóna, az előbbitől független, hozzá képest "nemfolytonos" zóna, amelyben az áramlás a Helmholtz és Kirchhoff által kidolgozott módszerekkel írható le. Mégpedig a Lord Rayleigh által bevezetett ellenállási képlettel, amely a relatív sebesség négyzetével arányos. Az elméletből – ebben a pillanatban (1911-ben) – hiányzik az a jellegzetes "szívó hatás", aminek eredménye az ellenállási mechanizmus, amit viszont a kísérletek már ki tudnak mutatni. Röviden szólva: üres beszédnek tűnik a közegben mozgó test mögött kialakuló, úgynevezett "holt tér", amit a mozgó test magával vonszol. A kérdés pontosan fogalmazva tehát az, hogy mi van az áramlásba helyezett test mögött? Ez a kérdés a most vizsgált Kármán-dolgozatok igazi tárgya.
Az első dolgozat – elkerülve az áramlásban lévő merev test pontos geometriai alakját(!) – két örvényfonalat vesz kiindulásul, amelyek egyenként azonos pörgésirányú örvények, szabályos távolságra egymást követően a sorokban. Természetesen a pörgésirány mindkét oldalon, vagy pedig váltakozva, hol az egyik, hol a másik oldalon, az egymást követő örvények l távolságának felével eltolva. A számítás eredménye az, hogy csak az utóbbi eset valósul meg a természetben, csak ez lesz stabil, éspedig abban az esetben, ha a h/l hányados meghatározott értékű. Itt h a két örvénysor közti távolság, l – mint említettük – az örvények közti távolság az egyes örvénysorban (1. ábra, Kármán eredeti rajza az [1] cikkből és 2. ábra: Kármán az örvénysorral). Az örvénysorokra felírt differenciálegyenletek elemzéséből az örvénysorok u sebességére adódik:
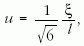
ahol ξ az örvényerősség.
Kármán Tódor nyomán az ellenállás-mechanizmust a következő módon magyarázzuk. A nyugvó folyadékban a test U sebességgel halad az x irányban. A test mögött emiatt örvényes mozgás alakul ki, amely a testtől bizonyos távolságra már a fent kiszámított stabil konfigurációtól alig tér el. Ez a mozgásállapot a testhez rögzített vonatkoztatási rendszerben nem stacionárius, hiszen az örvénysorok csak u < U sebességgel terjednek. Ez vezet arra, hogy az örvénysorok leszakadnak a testről – miközben újból keletkeznek a test mögött. A leszakadó örvénysorok a folyadékhoz képest U-u sebességgel mozognak, ez impulzust von el a testtől, ez vezet a közegellenálláshoz. Ezáltal ugyanis az örvénysorok U-u sebességkülönbséggel elszakadnak a testtől és ez a W ellenállási erőre a
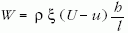
képletet adja. Most már csak a ξ örvényerősséget kell meghatározni. Abból kell kiindulni, hogy az izolált örvényfonal stabil állapota az instabil örvényrétegnek. Ezért tegyük fel, hogy az egyes örvényfonalak örvényerősségét megkaphatjuk, mint az l hosszúságú örvényréteg cirkulációjának összegét, hiszen ebből származik. Ezért
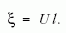
Ebből viszont az örvényrendszer terjedési sebességére
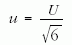
adódik. Így az ellenállási erőre kapjuk, hogy
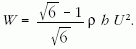
Előnyös, ha az általános szokásnak megfelelően bevezetjük a φ "ellenállási számot", amivel
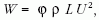
itt L a végtelen szélességűnek gondolt test valamilyen más, tetszőleges mérete (lemezvastagsága, ha körhenger, akkor annak átmérője stb.). Erre azért van szükség, hogy az elméleti elgondolás eredményét a tapasztalattal összehasonlíthassuk. Ezzel
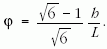
Ennyi az 1911. évből származó dolgozat [1] tömörített kivonata, amely mutatja, hogy az örvénysorokkal sikerült a négyzetes közegellenállási törvény mögé pillantani. Az első pozitívum: sikerült a fenomenológiai törvény mögött meghúzódó fizikai folyamatokat feltárni. Ezen eredmény jelentőségét nehéz úgy felmérni, hogy ne essünk túlzásba. Azokról a kimagasló eredményekről, amelyek a további évtizedekben mutatkoztak meg, az életrajz rövid folytatása során emlékezünk meg az alábbiakban.
Az örvénysorok problémaköre után Kármán még több érdekes kérdéssel foglalkozott, de az első világháború kitörése az ő életét is befolyásolta. Az akkor 33 éves göttingeni professzor hazatért, mert behívót kapott. Halláskárosodása miatt hátországi szolgálatra rendelték. Közel egy évig egy csepeli ruharaktárban dolgozott, majd a Bécs melletti Fischamendbe került, ahol a Monarchia új fegyverneme, a hadirepülő-arzenál központja volt (3. ábra). Itt végre a repüléssel lehetett foglalkozni, részt vehetett egy helikopteres konstrukció megvalósításában. Ez azt a cél szolgálta, hogy a tüzérség hatásosságát megfigyelhessék, a léggömbre helyezett szemlélő helyett az üteg felett egy helikopteren. Ez az alkotókról, Petróczy Istvánról, Kármán Tódorról és Zsurovetz Vilmosról elnevezett PKZ-jelű helikopter (4. ábra).
A háború végén Kármán Budapestre került, az oktatásügyi minisztériumban a felsőoktatási osztály vezetője lett. Ebben a minőségben vett részt Eötvös Loránd temetésén.
A következő években Aachenben találjuk, hiszen 1913-as professzori kinevezése nem évült el. Itt – úgy látszik – megtalálta helyét, egyetemi tanárként kedvére foglalkozhatott a repülés problémáival, lehetősége volt arra, hogy hatalmas szélcsatornát építsen a konstrukciók kísérleti vizsgálatára. Ez azonban ismét nem tarthatott soká. A békeszerződés Németországot többek között a repülőgépipar területén is korlátozta. A húszas évek még csak-csak elteltek. Ekkorra Kármán légügyi, a gépkonstrukciós kérdésekben már világszerte elfogadott, sőt keresett szaktekintély. 1933-ig ideje jelentős részében a világot járta, ahová szakmai kérdésekben hívták a légitársaságok műszaki tanácskérések során. A hitleri hatalomátvétel előtt Kármán többekkel együtt úgy látta, hogy új "hazát" kell keresnie. Ezt az új hazát Robert Andrews Millikan (1868–1953) Nobel-díjas fizikus a California Institute of Technology (a kaliforniai műegyetem) akkori vezetője kínálta neki, aki Pasadenába hívta, tanszéket és kísérleti laboratóriumot ajánlva. Daniel Guggenheim, az amerikai "rézkirály" adománya segítségével megalapította a pasadenai kísérleti aerodinamikai laboratóriumot (amiből 1943 után a Jet Propulsion Laboratory lett). 1935-ben Kármán az Amerikai Egyesült Államok állampolgárságát is megkapta.
Az Egyesült Államokban nemcsak a pasadenai központ fejlesztésén dolgozott. Az amerikai repülésügy komplex fejlesztésébe kezdett, előbb a polgári, később az eredményeknek megfelelően a nagy távolságú szállítórepülők és a harci repülők terén is, már a II. világháború folyamán.
Közben egy sajátos esemény, a Tacoma-Narrows tengerszoros felett épített híd összeomlása újra előtérbe hozta az örvénysorok problémáját. 1940. november 7-én a Washington államban lévő, a szoros felett épített 853 m hosszú híd az erős szélben sajátos kilengések – először rezonanciajelenségnek értelmezett hatások – következében leszakadt. A tragédiát követően Kármán az Engineering News Record hasábjain nyílt levélben megírta, hogy nézete szerint a híd berezgését a széláram hatására kialakuló és leszakadó örvénysorok okozták. Az esemény után természetesen műszaki vizsgálóbizottság alakult, amelynek tagjai sorába őt is meghívták. A híd újjáépítési munkálatai megkezdődtek, az ő javaslatait is figyelembe vették. Az új híd 1950-ben készült el, áramvonalas alakja jelentősen csökkentette az örvénysorok kialakulásának lehetőségét, és a híd még ma is áll.
A II. világháború alatt az Egyesült Államok kormányának légügyi szakértőjeként dolgozott. Számos gyakorlati javaslata vált be, csak azt emeljük most ki, hogy a nagy hatótávolságú bombázó és vadászrepülők üzemanyaggal való – repülés közben végrehajtott – újratöltését (egy másik repülőgépről) az ő elgondolása alapján vezették be.
A múlt század negyvenes éveitől kezdve Kármán Tódor a repülésügynek nemcsak az azonnali korszerűsítését tekintette kikerülhetetlen feladatnak. Az egész légi közlekedés minden kérdésében rendszeres, az oktatás részleteit is mozgósító előadásokat szervezett, ezek nagy részét ő maga tartotta. Az úttörő munka nemcsak a torlósugár-meghajtásra való áttérés, hanem az igazi rakétahajtás lehetőségeit is érintette. Csakhamar eljutott az interkontinentális, majd a kozmikus rakéták problémáihoz, ami mind a repülő testek alakját, mind a hajtóművek és hatóanyagok kérdését magában foglalta.
Ugyanakkor világos volt számára, hogy az egész "rakétaügy" két szektorra bomlik, az egyik az azonnali, "földi" alkalmazás, az Egyesült Államok hadi potenciálját érintő kérdés, a másik viszont az egész emberiség, az osztatlan "Kelet" és "Nyugat" közös ügye, a kozmikus űrhajózás kidolgozása. Ez utóbbit illetően egyik korszakalkotó diplomáciai eredménye a "Nemzetközi Asztronautikai Föderáció" (az egyes országok asztronautikai célú egyesületeinek összefogására szánt szövetség) megalakítása (1951). A másik pedig a világ minden asztronautikai témában eredményt elért kutató érdemi összefogásának és elismerésének célját szolgáló "Nemzetközi Asztronautikai Akadémia" megszervezése, ahol ténylegesen minden tevékenység számított, ami az asztronautika jelenét és jövőjét befolyásolhatja, a jogi kérdésektől kezdve a gyakorlati űrkutatás orvosi, mérnöki, konstrukciós, csillagászati stb. problémáit felölelve (1960).
Nem csoda tehát, hogy Kármán Tódor, a gépészmérnök, a repülésügy szakértője, a modern repüléstechnika nemzetközi előmozdítója, az asztronautika igencsak tevékeny szakembere 1963-ban J. F. Kennedytől, az Egyesült Államok elnökétől a National Medal of Science első példányát kaphatta meg egész tudományos tevékenysége elismeréséül (5. ábra).
Tudományos munkáinak gyűjteményes kiadása 1956-ban jelent meg [10].
Születésének századik évfordulóján, az Egyesült Államok emlékbélyeg kiadásával emlékezett meg az "Aerospace Scientist"-ről, vagyis "a repülés és űrrepülés tudósáról" (6. ábra).
Hogy a tudós világ milyen nagy becsben tartja őt, arra jellemző: a Hold túlsó oldalán (7. ábra) és a Marson is egy-egy kráter elnevezése őrzi emlékét.
Az örvénysorok napjainkban is elő-elő kerülnek. Egy műholdas felvétel révén a felhőkben kirajzolódó örvénysor látható, ami Guadelupe szigetének hegyei miatt alakult ki. A felvételt egy NASA műholdon elhelyezett kamera készítette 2012. június 20-án (8. ábra).
E sorok írója itt szeretne köszönetet mondani azoknak, akiknek segítsége és találékonysága nélkül ezt a munkát nem tudta volna elvégezni. Scharnitzky Viktorné Borika könyvtáros szakértelmének és lelkes támogatásának köszönöm az [1] és a [10] irodalom felkutatásának eredményét. Kendefi András figyelme nélkül mindörökre rejtve maradt volna az örvénygyűrűk Guadelupe-szigeti képe. Mindkettőjüknek hálás köszönet a segítségükért.