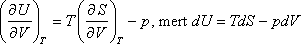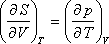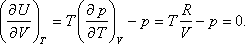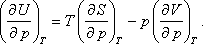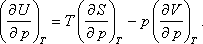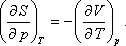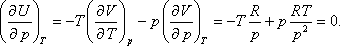A JOULE-THOMSON EFFEKTUS
Radnai Gyula
ELTE, Általános Fizika Tanszék
1. Az ideális gáz belső energiája
Az állandó tömegű ideális gáz egyszerű termodinamikai rendszer, mivel egyensúlyi állapotát két független állapotjelző egyértelműen
meghatározza [1,2].
Ha független állapotjelzőkül a nyomást és a térfogatot választjuk, akkor az ideális gáz hőmérséklete az alábbi termikus
állapotegyenletből kapható meg:
pV = RT (n = 1 mólra)
Az ideális gáz belső energiáját pedig az alábbi kalorikus állapotfüggvény szolgáltatja:
U = U (p, V)
A fenomenologikus termodinamikának főtételekre alapozott tárgyalásakor a nulladik főtétel biztosítja a hőmérséklet egzisztenciáját, az első főtétel pedig a belső energia, egzisztenciáját minden termodinamikai rendszerre. Így még a második főtétel előtt definiálhatunk egy empirikus hőmérsékleti skálát, valamelyik termodinamikai rendszer termikus állapotegyenletének felhasználásával.
A szokásos eljárás az, hogy referencia rendszernek éppen az ideális gázt választjuk, mert a pV = RT állapotegyenletben a
gázok anyagi minőségétől való függés nem szerepel. (Joggal választhatnánk például az ideális paramágneses szilárd anyagot is; az
ideális gáz választásának történeti oka van.)
A második főtétel az entrópia egzisztenciáját biztosítja. Kiterjesztve az entrópia fogalmát összetett rendszerek nem egyensúlyi
állapotaira is, a második főtétel segítségével a folyamatok irányára is következtethetünk. Csupán egyensúlyi állapotokon keresztül
történő idealizált folyamatok esetén is lehetővé válik azonban a második főtétel alapján egy olyan univerzális hőmérsékleti skála
definiálása, amely független a hőmérsékletet mérő anyag állapotegyenletétől:
 munkavégzés nélkül
munkavégzés nélkül
Vajon a pV = RT állapotegyenlettel definiált "ideális gáz hőmérsékleti skála” alkalmas-e olyan univerzális, „abszolút”
hőmérsékleti skálának, amelynek létezését a második főtétel mondja csak ki? Igen.
Egy közvetett bizonyíték lehet a következő eljárás:
- Feltesszük, hogy ideális gázra
pV = RT
úgy, hogy T most a második főtétel segítségével definiált abszolút hőmérséklet.
- Bebizonyítjuk a második főtétel felhasználásával, hogy ebben az esetben az ideális gáz belső energiája független a gáz
térfogatától és nyomásától, csak abszolút hőmérsékletétől függhet. A térfogattól való függés:
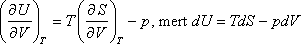
Felhasználva a következő Maxwell relációt:
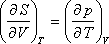
kapjuk:
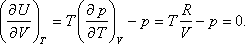
A nyomástól való függés:
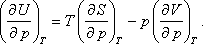
Felhasználhatjuk a következő Maxwell relációt:
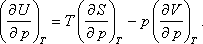
Így kapjuk:
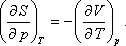
- Feltesszük, hogy ideális gázra a
pV=RT
egyenlet nem más, mint T definíciója, vagyis a
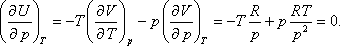
mennyiség egy empirikus, úgynevezett „ideális gáz hőmérséklet”, és e definíció alapján gőzhőmérőt készíthetünk.
- Megvizsgáljuk kísérletileg, vajon igaz-e, hogy az ideális gáz belső energiája csak a pV szorzattól függ.
Vagyis megvizsgáljuk, hogy igaz-e a 2. pontban bebizonyított állítás akkor is, ha a pV = RT-ben T az ideális
gázzal hitelesített hőmérsékleti skála.
Egyik ilyen kísérlet az, amikor összehasonlítjuk az ideális gáz két tetszőleges olyan egyensúlyi állapotát, melyben belső energiája
(és mólszáma) egyenlő, de nyomása és térfogata is más-más értékű.
Megmérjük mindkét állapotban a hőmérsékletet (empirikus, ideális gáz skálán), és megvizsgáljuk, egyenlő-e a két hőmérséklet.
Ha igen, akkor ez azt jelenti, hogy az ideális gáz belső energiája csak a pV = RT-vel definiált empirikus, ideális gáz
hőmérséklettől függ.
Elvileg megfelelő kísérlet erre az, amelyet először (1807-ben) Gay-Lussac végzett el, majd Joule a múlt század 40-es éveiben
megismételt, részleteiben is megvizsgált.
- Ha kísérletileg is megfelelő igazolást nyer az a feltételezés, hogy az ideális gáz belső energiája csak az ideális gáz
hőmérséklettől függ, akkor ebből már az első főtétel alapján következik, hogy az ideális gáz egy izotermikus folyamatban
ugyanannyi hőt vesz fel, mint amennyi munkát végez, s egy Carnot körfolyamatban a felvett és a leadott hők abszolút értékeinek
hányadosa az ideális gáz hőmérsékletek hányadosával egyezik meg.
Ugyanez igaz azonban a második főtétellel definiált abszolút hőmérsékletek hányadosára is!
Ez azt jelenti, hogy az ideális gáz hőmérséklet arányos az abszolút hőmérséklettel.
Kényelmi okokból az arányossági tényezőt 1-nek választjuk, s így az ideális gáz hőmérsékleti skála egyben abszolút hőmérsékleti
skála lesz.
(Mechanikában hasonló eljárást követünk akkor, amikor a gravitációs és a tehetetlen tömeg arányosságát bizonyító kísérletek -
Eötvös, Renner, Dicke és mások kísérletei - közös eredményeként, egyenlőnek választjuk a kétféle módon definiált tömeg
mértékegységét és mértékszámát.)
Fizikatörténeti háttér
Gay-Lussac a gázok közös viselkedését kutatta, az ideális gáz fogalma akkor még nem létezett. éppen az ő vizsgálatai vezettek
azonban az ideális gáz absztrakciójához. Felállította alaptörvényeit, amelyeket 1807-ben saját és mások kísérleti tapasztalataira
támaszkodva a következőképpen mondott ki: [3].
- Valamennyi gáz eredeti térfogatának 1/267 részével terjed ki, ha hőmérsékletét 1 fokkal növeljük;
- A gázok kitágulása független a nyomástól.
 munkavégzés nélkül
munkavégzés nélkül munkavégzés nélkül
munkavégzés nélkül