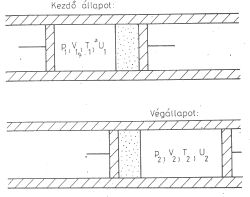
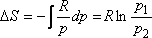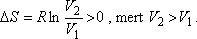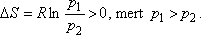Ezt az alábbi ábrákkal lehet szemléltetni (4. ábra).
Állítás:
U1+ p1Vl = U2 +
p2V2
Bizonyítás: Az első főtétel értelmében
U2 - U1= Q + W
Most Q = 0 az adiabatikus szigetelés miatt,
W = p1V1 - p2V2
mert a baloldali dugattyú lenyomásakor p1V1 munkát végzünk, a
jobboldali dugattyú elmozdulása közben pedig p2V2 munkát
nyerünk. A befektetett munka így a kettő különbsége.
Átrendezés után kapjuk a bizonyítandó állítást.
A H = U + pV mennyiséget entalpiának nevezzük, így a Joule-Thomson kísérletben
H1 = H2
mindig, akármilyen gázzal végezzük is azt el. A gáz új egyensúlyi állapota tehát mindig ugyanolyan
entalpiájú, mint a kiindulási állapot volt.
Ideális gázra pV = RT, tehát U = H - RT, vagyis ez a kísérlet ugyanúgy alkalmas
annak az igazolására, hogy a belső energia csak a hőmérséklet függvénye, mint a Gay-Lussac kísérlet.
Ha pedig T a második főtétellel definiált abszolút hőmérsékletet jelenti, akkor a Gay-Lussac
kísérlethez hasonlóan ez is alkalmas lesz az abszolút hőmérsékleti skála és az ideális gáz hőmérsékleti
skála egyenértékűségének bizonyítására, s közvetve a második főtételbe vetett bizalmunk
megerősítésére.
Csupán azt kell a méréssel ellenőriznünk, igaz-e, hogy T1= T2.
Viszont óriási különbség van a Gay-Lussac kísérlet és a Joule-Thomson kísérlet mérési
megbízhatósága, pontossága között!
Itt közvetlenül a gáz hőmérsékletét mérjük a kis hőkapacitású termoelemekkel, ezért a hőmérsékletmérés
pontossága legalább egy nagyságrenddel nagyobb.
Másrészt a Joule-Thomson kísérletben nem egy meghatározott, korlátozott tömegű gáz
állapotváltozását vagyunk kénytelenek megvizsgálni, mint a Gay-Lussac kísérletben, hanem megfelelő
kompresszort és nyomásszabályozókat csatlakoztatva a henger két oldalára, a nyomásokat
szabályozottan állandó értékeken tudjuk tartani, s így tetszőleges mennyiségű gáz állapotváltozását
tudjuk figyelemmel kísérni. A Joule-Thomson kísérlet során kivárhatjuk a stacionárius (időben állandó)
folyamat kialakulását. Az egyetlen probléma a jó hőszigetelés megvalósítása, az ebből eredő hiba
csökkentésére helyezzük el a termoelemeket a fojtás közelében.
Mivel a Joule-Thomson kísérlet is olyan irreverzibilis folyamat, ahol a kezdő és végállapot
egyensúlyi, ezért itt is kiszámítható az entrópianövekedés, a Gay-Lussac kísérlethez hasonló módon.
Tekintsünk egy egyensúlyi, izentalpikus folyamatot:
TdS = dU + pdV
TdS = d(U + pV) - Vdp
TdS = dH - Vdp
dH = 0, tehát
TdS = -Vdp
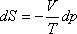
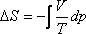 Mivel a Joule-Thomson kísérletben p2 < p1, ezért a
helyettesítő egyensúlyi folyamatban
Mivel a Joule-Thomson kísérletben p2 < p1, ezért a
helyettesítő egyensúlyi folyamatban
dp < 0
.
kell, hogy legyen. Tekintettel arra, hogy V > 0, és T > 0, ezért szükségképpen
ΔS > 0.
Egy mól ideális gázra 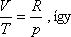 , így
, így
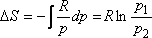
Az egyensúlyi folyamat során ugyanennyivel csökken a folyamatban
résztvevő hőtartályok összentrópiája, viszont az irreverzibilis Joule-Thomson
kísérletben ez a kompenzáló entrópiacsökkenés hiányzik, mivel a gáz
környezettől adiabatikusan el van szigetelve.
Hasonlítsuk össze egy mól ideális gáz entrópiaváltozását a két kísérletben!
Gay-Lussac kísérlet:
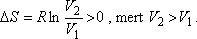
Joule -Thomson-kísérlet:
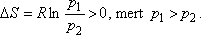
A Gay-Lussac kísérletben V2 / V1 = 2 volt, a Joule-Thomson
kísérletben azonban p1 / p2 = 200 is lehet!
Reális gázok esetén is sokkal nagyobb a tömegegységre
jutó entrópianövekedés a Joule-Thomson kísérletben, mint a Gay-Lussac kísérletben. Ez is oka annak,
hogy a reális gázok esetén mérhető hőmérsékletváltozás sokkal nagyobb a Joule-Thomson kísérletben,
mint a GayLussac kísérletben.
Hőmérsékletváltozások a Joule-Thomson-effektus során
Ha 200 atm-ról 1 atm-ra csökkentjük az eredetileg 52 °C-os levegő nyomását, akkor
hőmérséklete 23 °C-ra csökken. Ha 52 °C-os hélium nyomását csökkentjük 200 atm-ról
1 atm-ra, akkor a hélium 64 °C-ra melegszik fel. Tipikus hűtőközegek az ammónia és a freon 12.
Ha ezek hőmérsékletét akarjuk 30 °C-ról -15 °C-ra csökkenteni a Joule-Thomson effektus
segítségével, akkor az ammónia nyomását például 12 atm-ról 2,4 atm-ra, a freon 12 nyomását pedig
elég 7 atm-ról 1,8 atm-ra csökkenteni.
Általánosan jellemző kísérleti tapasztalat, hogy a kritikus nyomásnál legalább egy nagyságrenddel
nagyobb kezdőnyomásról indulva mind hőmérsékletcsökkenés, mind hőmérsékletemelkedés
lehetséges a Joule-Thomson kísérletben. Ez csak attól függ, hogy milyen a végállapotbeli nyomás.
Kivételt képeznek azonban például az igen magas hőmérsékletű kezdőállapotok, ekkor a
Joule-Thomson effektus mindig a hőmérséklet emelkedéséhez vezet.
Példaképpen nézzük meg a túlhevített vízgőz esetét. Ennek kritikus hőmérséklete
374 °C = 647 K, kritikus nyomása 225 atm. A mérnöki gyakorlatban használatos
vízgőztáblázatokból kiolvasható, hogy ha mondjuk 2 atm-ról 1 atm-ra fojtjuk le a
túlhevített vízgőz nyomását Joule-Thomson-effektus segítségével, akkor 130 °C-ról
indulva 4,5 °C-os hőmérsékletcsökkenést, 165 °C-ról indulva 3 °C-os csökkenést,
500 °C-ról indulva 0,5 °C-os csökkenést kapunk. Ahhoz, hogy a hőmérséklet ne
csökkenjen, hanem emelkedjék, a kiindulási hőmérsékletet jóval 1000 °C fölé kellene emelni.
Olyan magasra amikor viszont a H2O molekulák a nagy sebességű ütközések

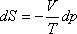
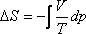 Mivel a Joule-Thomson kísérletben p2 < p1, ezért a
helyettesítő egyensúlyi folyamatban
Mivel a Joule-Thomson kísérletben p2 < p1, ezért a
helyettesítő egyensúlyi folyamatban
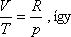 , így
, így