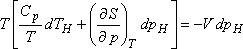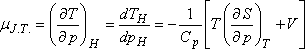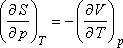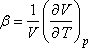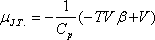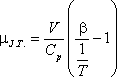következtében részben gerjesztődnének, esetleg ionizálódhatnak is, s ekkor már nem az eredeti gázról
lenne szó. A mérnöki vízgőztáblázatokban nem is találunk 1000 °C-nál nagyobb hőmérséklethez
tartozó adatokat.
A Joule-Thomson-effektus adta hőmérsékletváltozás azonban nem csak a kiindulási hőmérséklettől,
hanem a kiindulási nyomástól is függ. Ha például az 500 °C-os vízgőz nyomását nem 2
atm-ról fojtjuk le 1 atm-ra, hanem 500 atm-ról 499 atm-ra, a hőmérsékletcsökkenés az
előbbi 0,5 °C-nak is csak a fele, 0,25 °C lesz. Ez azt mutatja, hogy elég magas nyomáson
az ilyen kis Δp értékkel való fojtás (ezt nevezik differenciális Joule-Thomson
effektusnak) előbb-utóbb hőmérsékletemelkedéshez vezet.
Persze ha az 500 °C-os, 500 atm nyomású vízgőz nyomását 1 atm-ra fojtjuk, (ez az igazi,
vagy "integrális" Joule-Thomson effektus) akkor hőmérséklete már jelentősen csökken, lehűl
122 °C-ra).
Nemcsak gázzal, hanem folyadékkal is elvégezhetjük a Joule-Thomson kísérletet. A H2O példájánál maradva
megvizsgálhatjuk, hogyan változik a víz hőmérséklete a fojtásos folyamat során. A víz entalpiája elég jó közelítésben csak a
hőmérséklet függvénye, így csak nagyon kis hőmérsékletváltozásokat várhatunk. Induljunk ki itt is az 500 atm nyomású
kezdőállapotból, legyen a kezdőhőmérséklet 273 °C (= 546 K). Ha követjük azt a izentalp görbét, amely ezen a
kezdőállapoton halad át a p; T diagramon, akkor az alábbi p, T értékpárokhoz jutunk:
p; 500 atm 400 atm 300 atm 200 atm 100 atm
T; 273,0 °C 273,2 °C 273,4 °C 273,3 °C 272,8 °C
Ez azt jelenti, hogy ha az 500 atm nyomású 273 °C hőmérsékletű H2O fluidumot 400 atm-ra fojtjuk,
akkor 0,2 °C-kal felmelegszik, ha viszont 100 atm-ra fojtjuk, akkor 0,2 °C-kal lehűl. Ha éppen 125 atm-ra fojtanánk,
hőmérséklete pontosan ugyanannyi lenne, mint a kiindulási állapotban volt.
Nemcsak ideális gázra jellemző tehát, hogy a Joule-Thomson folyamatban nincs hőmérsékletváltozás.
Minden tiszta anyagra, nem túl kicsi és nem túl nagy
hőmérsékletek esetén akármelyik hőmérséklethez tartozik tetszőlegesen sok olyan (p, p') nyomás értékpár, amelyek
entalpiája egyenlő egymással.
Ekkor a nagyobb nyomásról a megfelelő kisebb nyomásra fojtva az anyagot, hőmérséklete nem változik meg. Az előbb említett
273 °C vizet 500 atm-ról 125 atm-ra, vagy 400 atm-ról 175 atm-ra vagy 350 atm-ról 250 atm-ra fojtva nem lesz
hőmérsékletváltozás. A differenciális Joule-Thomson effektus során ezen a hőmérsékleten kb. 300 atm nyomáson nem lesz
hőmérsékletváltozás.
Joule-Thomson koefficiens
A víz most leírt viselkedése a tiszta anyagokra általában is jellemző, s az alábbi ábrákon foglalható össze:
(5. ábra.).
A p; T koordinátarendszerben az olyan p*, T* állapot, amely esetén a differenciális Joule-Thomson-effektusban
nincs hőmérsékletváltozás, mindig egy izentalp görbének a legnagyobb hőmérsékletű állapota. Látszik, hogy ugyanilyen entalpiájú,
de p*-nál kisebb nyomású állapotok esetén differenciális Joule-Thomson-effektus során a hőmérséklet csökken,
p*-nál nagyobb nyomások esetén nő. Ezért a p*, T* állapotot a megfelelő entalpiához tartozó "inverziós
állapotnak" hívják, itt "fordul meg" (invertálódik) a differenciális Joule-Thomson-effektus kimenetele.
A differenciális Joule-Thomson-effektus eredményének mennyiségi jellemzésére vezették be az ún. JouleThomson-koefficienst
(µJ.T.,) az alábbi definícióval:
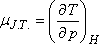
Az egyensúlyi termodinamika alapösszefüggései segítségével µJ.T.-t az anyag más jellemzőivel is
összekapcsolhatjuk:
TdS = dU + pdV
TdS = d(U + pV) - Vdp
TdS = dH -Vdp
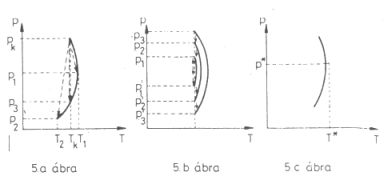
5. ábra. Állandó entalpiájú (izentalp) görbék és fojtásos folyamatok ábrázolása a (p; T) koordinátarendszerben
5. a. ábra. A kezdeti (pk, Tk) állapotból melegebb
(p1, T1) és hidegebb (p2, T2)
állapotba is átmehet az anyag. Ha nyomását éppen p3-ra csökkentjük, hőmérséklete nem változik.
5. b. ábra. Ugyanahhoz a hőmérséklethez tetszőleges sok olyan (pi, pi') nyomás
értékpár tartozik, amelyek esetén nem lesz hőmérsékletváltozás a Joule-Thomson-kísérletben.
5. c. ábra. Egy kiválasztott T* hőmérséklethez tartozó p* nyomás, amely esetén a differenciális
Joule-Thomson effektusban nem lesz hőmérsékletváltozás
Legyenek az extenzív állapotjelzők (S, H, V) p és T függvényei. Ekkor S = S (p,T) teljes
differenciálja:
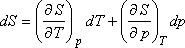
Másrészt
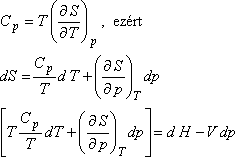
Tekintsük azt a speciális esetet, amikor dH< /I>= 0, mivel 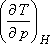 -t
akarjuk meghatározni:
-t
akarjuk meghatározni:
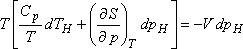
Ebből az egyenletből:
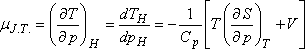
Szemléletesebb kifejezést kapunk, ha felhasználjuk a következő Maxwell relációt:
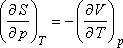
valamint a térfogati hőtágulási együttható alábbi definícióját:
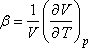
Ezekkel
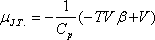
ami így is írható:
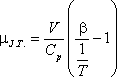
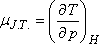
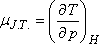

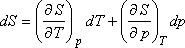
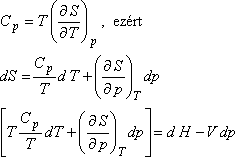
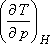 -t
akarjuk meghatározni:
-t
akarjuk meghatározni: