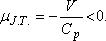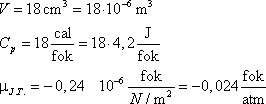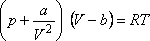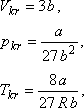A most levezetett összefüggésünk alapján a Joule-Thomson-koefficiens előjelét
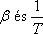 viszonyával tudjuk összekapcsolni.
Az anyagnak azokban az állapotaiban, ahol
viszonyával tudjuk összekapcsolni.
Az anyagnak azokban az állapotaiban, ahol 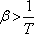 a Joule-Thomson-koefficiens pozitív, tehát a differenciális Joule-Thomson-effektus során az anyag
hőmérséklete csökken.
a Joule-Thomson-koefficiens pozitív, tehát a differenciális Joule-Thomson-effektus során az anyag
hőmérséklete csökken. 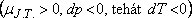 Ha viszont
Ha viszont
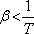 ,
akkor az anyag melegszik. Abban az esetben, amikor
,
akkor az anyag melegszik. Abban az esetben, amikor 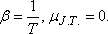 .
Ez éppen az ideális gáz esetén valósul meg, hiszen az ideális gázra
.
Ez éppen az ideális gáz esetén valósul meg, hiszen az ideális gázra
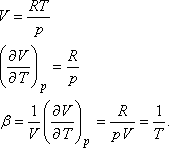
Térjünk vissza a víz példájához. A víz hőtágulási együtthatója 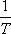 -hez
képest rendkívül kicsi (0 °C és 4 °C között negatív, 4 °C-on zérus, 4 °C és
100 °C között pozitív - 1 atm nyomáson), ezért jó közelítésben a JouleThomson koefficiens
vízre:
-hez
képest rendkívül kicsi (0 °C és 4 °C között negatív, 4 °C-on zérus, 4 °C és
100 °C között pozitív - 1 atm nyomáson), ezért jó közelítésben a JouleThomson koefficiens
vízre:
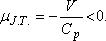
Vagyis a víznek melegednie kell a fojtásos folyamatban. Behelyettesítve a mólnyi mennyiségű vízre
jellemző adatokat:
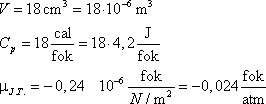
A várható hőmérsékletemelkedés 1000 atm nyomásesés esetén 24 °C. Ez a becslés jól egyezik
a víz-vízgőz táblázatokból kiolvasható értékkel.
Felmerül a kérdés: a szokásos, szobahőmérsékletű víznek nincs inverziós pontja? Miért mindig csak
melegszik a Joule-Thomson-effektus során?
Említettük, hogy az inverziós állapot minden tiszta anyagra így H2O-ra is csak
nem túl kicsi és nem túl nagy hőmérsékleteken léphet fel. Ez a hőmérsékletintervallum nagyon tág, és
általában a hármasponti és a kritikus hőmérséklet közötti értéktől a kritikus (abszolút) hőmérséklet
többszöröséig tart. Vízre az alsó határ 234 °C körül van (kb. 507 K). Ennél alacsonyabb
hőmérsékleteken a folyadék víz csak melegszik a fojtásos folyamatban.
Az inverziós görbe
Az inverziós állapotokat ábrázoló pontok a p;T koordinátarendszerben egy maximummal
rendelkező görbén helyezkednek el, amely valahol a folyadék-gőz fázishatár görbéről indul jóval a
kritikus hőmérséklet után éri el újra a T tengelyt (6. ábra).
Ezt az utóbbi határhőmérsékletet, amely a lehetséges legnagyobb inverziós hőmérséklet nevezik gyakran
egyszerűen inverziós hőmérsékletnek. Fontos jelentése van: ha Joule-Thomson effektussal
hőmérsékletcsökkenést szeretnénk elérni, akkor az anyag kiindulási hőmérsékletének ennél kisebbnek
kell lennie. H2O esetén persze ez egy olyan óriási hőmérséklet, hogy a kérdés feltevése
se indokolt. Az inverziós hőmérséklet levegő esetén még 330 °C, hidrogén és különösen hélium
esetén azonban jóval a szobahőmérséklet alatt van. Hidrogénre -71 °C = 202 K, ami a hidrogén
kritikus hőmérsékletének (33,3 K-nak) még mindig kb. a hatszorosa. Nitrogénre a maximális inverziós
hőmérséklet a kritikus hőmérséklet ötszöröse, héliumra pedig 7,7-szerese (kb. 40 K).
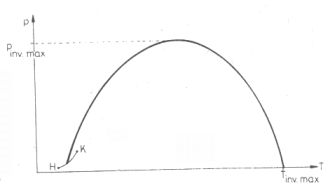
6. ábra. Inverziós görbe a (p; T) koordinátarendszerben.
H = Hármaspont (a gáz, a folyadék és a szilárd fázis közös egyensúlyi állapota),
K = Kritikus pont (a H-t K-val összekötő, ún. folyadék-gáz fázishatárgörbén
vannak a telített gőz állapotok)
Tinv.max. = a legnagyobb inverziós hőmérséklet
pinv.max. = a legnagyobb inverziós nyomás
Az inverziós görbe alatti tartományban µJ.T. > 0, az inverziós görbén
µJ.T. = 0, felette pedig µJ.T. < 0.
A folyadék-gáz fázisgörbe alatt a Joule-Thomson-
koefficiens pozitív, tehát pl. a vízgőzt 234 °C hőmérséklet alatt is lehet hűteni Joule-Thomson-effektussal.
(234 °C-on és 30 atm nyomáson éri el H2O esetén az inverziós görbe a víz-vízgőz
fázishatárgörbét). A 10 atm-ás 190 °C hőmérsékletű vízgőz hőmérséklete 163 °C-ra csökken,
ha fojtással a nyomását 1 atm-ra csökkentjük. A 2 atm-ás 120°°C-os vízgőz hőmérséklete
111 °C-ra csökken, ha 1 atm-ra tágul ki a fojtásos folyamatban (kuktafazék szelepén kiáramló eset),
az 1 atm-ás 100 °C-os vízgőzt 0,01 atm-ra fojtva pedig 93 °C lesz a hőmérséklete.
Ha összehasonlítjuk különböző gázok inverziós hőmérsékleteinek mért értékeit, ez ugyanolyan nagy
változatosságot mutat, mint amilyen változatosak a kritikus hőmérséklet mért értékei. A kettő
hányadosa azonban már sokkal kevésbé változik. Tájékozódásul álljon itt néhányjellemző adat:
[9]
| Tkr | Tinv.max |
Tinv.max/Tkr |
| N2 | 126 K |
621 K | 4,9 |
| levegő | 132 K |
603 K | 4,6 |
| Ar | 151 K |
723 K | 4,8 |
| H2 | 33,3 K |
202 K | 6,1 |
| He | 5,2 K |
40 K | 7,7 |
| pkr | pinv.max |
pinv.max/pkr |
| N2 | 33,5 atm |
400 atm | 12 |
| H2 | 12,8 atm |
106 atm | 13 |
| He | 2,3 atm |
37 atm | 16 |
A fenti táblázatban nemcsak a maximális inverziós hőmérsékletet, hanem az inverziós görbe
maximumához tartozó nyomást is összehasonlítottuk a kritikus állapothoz tartozó megfelelő
értékekkel.
Érdemes ezek után megnézni, hogy a reális gázokra leggyakrabban használt állapotegyenletek -
melyeket molekuláris fizikai meggondolásokból kaphatunk mennyire jól adják ezeket az értékeket. A
legismertebb ilyen állapotegyenlet a van der Waals állapotegyenlet:
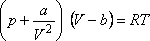
Az ebben szereplő a, b, R paraméterekkel a kritikus térfogat, nyomás és hőmérséklet az
alábbi módon fejezhető ki (l. pl. [10]):
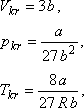
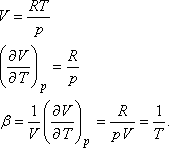
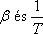 viszonyával tudjuk összekapcsolni.
Az anyagnak azokban az állapotaiban, ahol
viszonyával tudjuk összekapcsolni.
Az anyagnak azokban az állapotaiban, ahol 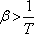 a Joule-Thomson-koefficiens pozitív, tehát a differenciális Joule-Thomson-effektus során az anyag
hőmérséklete csökken.
a Joule-Thomson-koefficiens pozitív, tehát a differenciális Joule-Thomson-effektus során az anyag
hőmérséklete csökken. 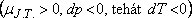 Ha viszont
Ha viszont
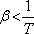 ,
akkor az anyag melegszik. Abban az esetben, amikor
,
akkor az anyag melegszik. Abban az esetben, amikor 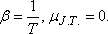 .
Ez éppen az ideális gáz esetén valósul meg, hiszen az ideális gázra
.
Ez éppen az ideális gáz esetén valósul meg, hiszen az ideális gázra
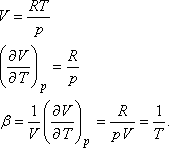
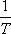 -hez
képest rendkívül kicsi (0 °C és 4 °C között negatív, 4 °C-on zérus, 4 °C és
100 °C között pozitív - 1 atm nyomáson), ezért jó közelítésben a JouleThomson koefficiens
vízre:
-hez
képest rendkívül kicsi (0 °C és 4 °C között negatív, 4 °C-on zérus, 4 °C és
100 °C között pozitív - 1 atm nyomáson), ezért jó közelítésben a JouleThomson koefficiens
vízre: