Fizikai Szemle 1979/03. 88.o.
A foton
Ha egyetlen mondatban kellene válaszolni arra a kérdésre, hogy mi a foton, a válasz kétségtelenül csak az
lehetne, hogy a foton a fényrészecske neve. Márpedig a foton szót ma teljesen általánosan használják a
fizikában, irodalomban és előadásokban egyaránt. Ebből tehát arra a következtetésre lehetne jutni, hogy
a fény természetéről vallott mai felfogásunk szerint a fény részecskékből áll, amelyek természetesen
bizonyos bonyolult tulajdonságokkal rendelkezhetnek. (Pl, polarizációs irányuk van, stb.) Ez a következtetés
azonban elhamarkodott volna. A foton fogalma, azóta, amióta a század elején Einstein megalkotta,
érdekes és mélyértelmű fejlődésen ment keresztül. Ma már pontosan csak a kvantumelektrodinamika
keretén belül érthető meg és nem is lelet egy mondattal definiálni. A foton fogalmának megértése nélkül
azonban nem foglalhatunk állást ma is aktuális kérdésekkel szemben, amilyen például az az ismert
probléma, hogy a foton csak önmagával interferálhat-e, vagy interferálhatnak különböző fotonok is.
Tekintsük tehát át a fény természetéről vallott nézetek fejlődését az újkori fizika történetének során
és vizsgáljuk meg, hogy ma mit értünk foton alatt.
Mint ismeretes, a klasszikus fizika kezdeti szakában két elmélet állott szemben egymással: Newton
korpuszkuláris és Huyghens undulációs elmélete. Newtont elsősorban az a szempont vezette a
korpuszkuláris elmélet kialakításánál, hogy csak így tudta megmagyarázni, hogyan haladhat a fény
az üres téren át, pl. a Napról a Földre. A korpuszkuláris természet mellett szólt azonkívül a fény
egyenesvonalú terjedése és az éles árnyék, jól lehetett magyarázni a tükrön való visszaverődés
jelenségét is rugalmas golyók visszaverődésének mintájára. Ismeretes továbbá, hogy a fénytörés
jelenségét is látszólag jól lehetett magyarázni azzal a feltevéssel, hogy a sűrűbb közeg nagyobb
vonzóereje maga felé hajlítja a fénysugarat.
Ez az elmélet azonban csakhamar tarthatatlannak bizonyult. A pontosabb megfigyelés azt mutatta, hogy
az egyenesvonalú terjedés és az éles árnyék képződése nem is felel meg a valóságnak, elhajlás lép
fel, (éspedig az elhajlási kép sokszor bonyolult struktúrát mutat, úgyhogy semmiképpen nem lehet
részecskefelfogással magyarázni). A fény terjedésére adott magyarázat sem állja meg a helyét. Először
is sokszor nem a sűrűbb anyag az »optikailag sűrűbb«, másodszor Newton elmélete
szerint a sűrűbb anyagban nagyobb a fénysebesség, ez pedig ellenkezik Fizeau kísérletének eredményével.
(Teljesség kedvéért megjegyezhetjük, hogy a tükrön való visszaverődés sem érthető rugalmas golyók
mintájára, ha tekintetbe vesszük, hogy még a legsimább tükör is atomi méretekben erősen
»göröngyös«). Végezetül pedig az interferenciajelenségeknek
(fény + fény = sötétség), melyek közül néhányat már Newton is ismert, a magyarázatát meg sem
lehet kísérelni korpuszkuláris alapon.
Huyghens hullámelméletével viszont az előbb felsorolt jelenségeket mind meg lehet magyarázni, azonban
természetesen szükséges feltételezni valamilyen anyagot, ami a hullámokat hordozza. Ezt az anyagot,
amely tehát a világűrt is betölti, nevezték el éternek. Feltették, hogy ez igen ritka, finom anyag, mert
hiszen a bolygókra gyakorolt fékező vagy egyéb mechanikai hatását nem észlelték. Az éterelmélet a 19.
század első felében nagy fejlődésen ment keresztül. Ebben elsősorban a polarizáció felfedezésének
volt nagy szerepe, mert ennek magyarázatára fel kellett tenni, hogy a fény transzverzális rezgés,
másszóval, hogy az éter a fényrezgésekkel szemben, mint rugalmas, szilárd anyag viselkedik. (Hogy
az égitestek mégis ellenállás nélkül haladhatnak benne, az azzal lenne magyarázható, hogy azok
mozgása nagyon lassú a fényrezgések üteméhez képest.) Kialakult a mechanikai fényelmélet,
amely a fényjelenségeket úgy akarta magyarázni, hogy egyszerűen megpróbálta a rugalmas kontinuumok
mechanikáját az éterre alkalmazni. Közben az elektromosság is rohamosan fejlődött, 1862-ben
sikerült Maxwellnek a róla elnevezett egyenletekben csodálatos tömörséggel és precizitással
összefoglalni az elektromágneses jelenségek törvényszerűségeit. Egyenletei alapján megjósolta
az elektromágneses hullámok létezését, sőt kimondta, hogy a fény nem más, mint nagyfrekvenciájú
elektromágneses hullám. Ezek után a mechanikai fényelméletnek az volt a feladata, hogy az
elektromágneses térnek immár pontosan ismert, a Maxwell-egyenletek által leírt tulajdonságait
az éter mechanikai tulajdonságaira vezesse vissza. Rengeteg fáradozás ellenére ez a törekvés
sikertelen maradt. Ezért már a század vége felé le is mondanak arról, hogy az éter tulajdonságait
mechanikai úton magyarázzák. Elfogadják azt a tényt, hogy az éter számára külön törvényszerűségek
állnak fenn, amelyeket éppen a Maxwell-egyenletek írnak le. Annál erősebben lép fel azonban az igény,
ezt a különleges anyagot valamilyen módon közvetlenül észlelni. Konkréten felmerült a kívánság,
a Naprendszernek vagy speciálisan a Földnek sebességét az éterhez képest megállapítani, az éterhez
képest mozgó Földön az éterszél hatását kimutatni. Ismeretes, hogy az ezzel a céllal elvégzett
Michelson-kísérlet eredménye negatív volt és a speciális relativitás-elméletnek lett a kísérleti alapja.
A mi szempontunkból most csak az elmélet alapvető megállapítása a fontos: Éter nincs. Mert hiszen
azonnal felmerül a kérdés: mi hordozza az elektromágneses hullámokat? Erősen hangsúlyozzuk,
hogy a fény naiv hullámelmélete már azzal a felismeréssel, hogy nem létezik a teret betöltő finom
anyag, megdőlt.
Hogy ezt a körülményt nem szokták hangsúlyozni, annak oka abban rejlik, hogy ugyanebben az időben
váltak ismeretessé a kvantumos jelenségek és az ezzel kapcsolatos megfontolások, amelyek a fizika
fejlődésének új forradalmi szakaszát indították meg, és amelyek egészen más oldalról támadták meg
a fény természetének hullámelméletét. Ismeretes, hogy Planck a fekete sugárzás törvényének
levezetésénél arra a feltevésre kényszerült, hogy az atomok csak diszkrét energiájú állapotokban
létezhetnek. Hogyan abszorbeálják akkor a fényt? A közönséges, klasszikusan elképzelt hullámtérből
nem vehetnek felugrásszerűen valamilyen véges, diszkrét energiamennyiséget, mert hiszen a szokásos
kísérleti feltételek mellett a klasszikus számítások szerint az átlagos energiasűrűség sokkal kisebb,
semhogy az atom a környezetéből ugrásszerűen akkora energiát tudjon felvenni, amennyit a
feketesugárzás magyarázatához fel kell tételezni. Kétféle magyarázattal próbálkozhatunk. Az abszorpció
vagy úgy történhet, hogy az atomok az energiát lassan összegyűjtik, felhalmozzák maguk körül s
aztán egyszerre elnyelik, vagy az energia már eleve csomókba koncentrálva van jelen a sugárzási
térben. Ugyanerre utal egy másik fontos tapasztalati tény, a fotoeffektus jelensége. Bizonyos
fémekből fény hatására elektronok lépnek ki. A kiváltott elektronok energiája a fény színétől, tehát
frekvenciájától függ, száma pedig a fény intenzitásától, éspedig az effektus rögtön a besugárzás
megindítása után fellép (tehát egészen minimális intenzitású fénynél is egy-két gyors elektron rögtön
megjelenik). A Maxwell-féle elmélet szerint ilyen rövid idő alatt az elektron semmiféleképpen nem
vehet fel akkora energiát a térből, amennyit tapasztalunk, csak akkor, ha a sugárzásban már eleve
koncentrált csomók alakjában jön az energia. Ezek az új tapasztalatok tehát azt mutatják, hogy a
fénynek eklatáns részecsketulajdonságai is vannak, amelyeket semmiképpen nem lehet az eddigi
hullámképpel magyarázni.
 Látjuk tehát, hogy sem a naiv részecske elképzelés, sem a naiv hullám elképzelés nem tudja kielégítően
leírni a fény természetével kapcsolatos tapasztalatokat. A súlyos dilemmából még két kiutat lehet
megpróbálni. A) A naiv hullámképet úgy módosítani, hogy a részecsketulajdonságok is beleférjenek.
B) Ugyanezt megfordítva, a naiv részecskeképet úgy módosítani, hogy a hullámtulajdonságok is
beleférjenek. Az első úttal próbálkozott meg 1905-ben Einstein, a tűsugárzás elméletének felállításával.
Eszerint a fény ugyan valóban elektromágneses hullám, azonban a térben kis hullámcsomagok alakjában
van jelen. Éspedig egy monokromatikus fénynyalábban a frekvencia v, ezeknek a kis
hullámvonulatoknak, hullámcsomagoknak az energiája hv, impulzusa hv/c. Ezeket a
csomókat nevezte Einstein fotonoknak. A fotonok segítségével az előbb említett két jelenség,
t. i. a fényemisszió, abszorbció és a fotoeffektus valóban érthetővé válik, sőt, mint ismeretes, a
kilépő fotoelektronok maximális energiájára vonatkozó Einstein-féle képlet vagy a színképvonalak
frekvenciáját megadó Bohr-féle frekvenciafeltétel kvantitatíve is teljes megegyezésben van a
tapasztalattal. A fotonok impulzusa szintén ellenőrizhető tapasztalatilag. Elsősorban a fénynyomást
kell említenünk, azonban ezt a Maxwell-elmélet is magyarázza. Ezen túlmenőleg azonban Einstein
1917-ben kimutatta, hogy a Maxwell-féle sebességeloszlás izzó gázokban csak akkor stacionárius,
ha az egyes fotonok éppen
Látjuk tehát, hogy sem a naiv részecske elképzelés, sem a naiv hullám elképzelés nem tudja kielégítően
leírni a fény természetével kapcsolatos tapasztalatokat. A súlyos dilemmából még két kiutat lehet
megpróbálni. A) A naiv hullámképet úgy módosítani, hogy a részecsketulajdonságok is beleférjenek.
B) Ugyanezt megfordítva, a naiv részecskeképet úgy módosítani, hogy a hullámtulajdonságok is
beleférjenek. Az első úttal próbálkozott meg 1905-ben Einstein, a tűsugárzás elméletének felállításával.
Eszerint a fény ugyan valóban elektromágneses hullám, azonban a térben kis hullámcsomagok alakjában
van jelen. Éspedig egy monokromatikus fénynyalábban a frekvencia v, ezeknek a kis
hullámvonulatoknak, hullámcsomagoknak az energiája hv, impulzusa hv/c. Ezeket a
csomókat nevezte Einstein fotonoknak. A fotonok segítségével az előbb említett két jelenség,
t. i. a fényemisszió, abszorbció és a fotoeffektus valóban érthetővé válik, sőt, mint ismeretes, a
kilépő fotoelektronok maximális energiájára vonatkozó Einstein-féle képlet vagy a színképvonalak
frekvenciáját megadó Bohr-féle frekvenciafeltétel kvantitatíve is teljes megegyezésben van a
tapasztalattal. A fotonok impulzusa szintén ellenőrizhető tapasztalatilag. Elsősorban a fénynyomást
kell említenünk, azonban ezt a Maxwell-elmélet is magyarázza. Ezen túlmenőleg azonban Einstein
1917-ben kimutatta, hogy a Maxwell-féle sebességeloszlás izzó gázokban csak akkor stacionárius,
ha az egyes fotonok éppen 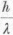 nagyságú impulzussal lökik hátra az atomot, mikor elhagyják.
Nézzük meg azonban, hogy mi a helyzet az interferencia jelenségével.
Kisszögű interferenciánál
a kísérletekre mégcsak találhatnánk magyarázatot e kép alapján. Nem találhattunk azonban magyarázatot
a nagyszögű interferencia-kísérletekre, amelyek közül az első Selényi Pál nevéhez fűződik
(lásd ábra). A P pontból ellentétes irányban kiinduló 1 és 2 fénysugár interferál, ami nem
egyeztethető össze az említett csomagképpel, hiszen a csomag vagy az egyik, vagy a másik ágban
indulna el és nem lehetne jelen egyszerre mindkettőben. Vagy nézzük meg hogyan tudnók magyarázni
az interferenciát a Michelson-féle interferométerben. Mindenekelőtt ismeretes, hogy az interferenciakép
jellege független az intenzitástól, egészen gyenge fény esetén is, ha az egyes csomagok már egyenként
jönnek, változatlan.
nagyságú impulzussal lökik hátra az atomot, mikor elhagyják.
Nézzük meg azonban, hogy mi a helyzet az interferencia jelenségével.
Kisszögű interferenciánál
a kísérletekre mégcsak találhatnánk magyarázatot e kép alapján. Nem találhattunk azonban magyarázatot
a nagyszögű interferencia-kísérletekre, amelyek közül az első Selényi Pál nevéhez fűződik
(lásd ábra). A P pontból ellentétes irányban kiinduló 1 és 2 fénysugár interferál, ami nem
egyeztethető össze az említett csomagképpel, hiszen a csomag vagy az egyik, vagy a másik ágban
indulna el és nem lehetne jelen egyszerre mindkettőben. Vagy nézzük meg hogyan tudnók magyarázni
az interferenciát a Michelson-féle interferométerben. Mindenekelőtt ismeretes, hogy az interferenciakép
jellege független az intenzitástól, egészen gyenge fény esetén is, ha az egyes csomagok már egyenként
jönnek, változatlan.

Az interferencia tehát csak úgy lenne elképzelhető, hogy a csomag a »C«
félig áteresztő tükrön kettészakad, az egyik fele megjárja az utat A-ig és vissza, a másik B-ig
és vissza. Ekkor azonban a két félcsomagot ki lehetne mutatni külön-külön, például A-nál és
B-nél elhelyezett számláló csövek segítségével. Cosyns elvégezte ezt a kísérletet és azt találta,
hogy az A-nál és B-nél elhelyezett számlálócsövek sohasem szólalnak meg egyszerre,
hanem statisztikusan vagy az egyik vagy a másik szólal meg, más szóval a foton csak egészében
abszorbeálódik, »feldarabolni« nem lehet. Ha tehát a csomagelképzelés helyes, akkor
azt kell mondanunk, hogy az egyes fotonok az A és B tükrök közül csak az egyiket
érintik. Ekkor azonban teljesen magyarázat nélkül maradt az interferencia. Talán még érdekesebbek
Rupp kísérletei. Az egyiknek vázoljuk a gondolatmenetét. Optikai rács mögött az ábrán látható
módon csősugarakat bocsátunk el közvetlenül a rács nyílásai mentén.
 A csősugarakban gerjesztett atomok repülnek, melyek fényt bocsátanak ki.
Mármost a tűsugárzás elmélete alapján a következő két eset lehetséges. 1. Vagy olyan gyorsan történik a
foton kisugárzása, hogy az egész csomag, az egész hullámvonulat egyetlen nyíláson megy át,
2. vagy pedig a hullámvonulat kibocsátása olyan hosszú idő alatt történik, hogy az alatt az atom sok
nyílás mellett elhalad, így mindegyik nyíláson a hullámvonulatnak csak egy kis darabja megy át. Az
energia egyenletesen eloszlik az egyes darabokra és így a megjelenő frekvencia az eredeti frekvenciának
a tört része lenne. Nos a tapasztalat szerint egyik eset sem következik be, hanem az történik, hogy az
eredeti frekvencia mellett két másik ú. n. tükörfrekvencia is megjelenik, ezeknek eltérése az eredetitől
pontosan megfelel a csősugárban repülő atomnak a rács egyes nyílásai elé való érkezése ütemének,
frekvenciájának. Úgy tűnik tehát, hogy az eredetitől különböző frekvenciájú fotonok kerülnek a térbe,
mégpedig a tűsugárzás szempontjából teljesen érthetetlen módon. Természetesen további nehézségek is
lennének ezeket azonban nem részletezzük, mert az eddigiek is mutatják ennek a képnek az elégtelenségét.
A csősugarakban gerjesztett atomok repülnek, melyek fényt bocsátanak ki.
Mármost a tűsugárzás elmélete alapján a következő két eset lehetséges. 1. Vagy olyan gyorsan történik a
foton kisugárzása, hogy az egész csomag, az egész hullámvonulat egyetlen nyíláson megy át,
2. vagy pedig a hullámvonulat kibocsátása olyan hosszú idő alatt történik, hogy az alatt az atom sok
nyílás mellett elhalad, így mindegyik nyíláson a hullámvonulatnak csak egy kis darabja megy át. Az
energia egyenletesen eloszlik az egyes darabokra és így a megjelenő frekvencia az eredeti frekvenciának
a tört része lenne. Nos a tapasztalat szerint egyik eset sem következik be, hanem az történik, hogy az
eredeti frekvencia mellett két másik ú. n. tükörfrekvencia is megjelenik, ezeknek eltérése az eredetitől
pontosan megfelel a csősugárban repülő atomnak a rács egyes nyílásai elé való érkezése ütemének,
frekvenciájának. Úgy tűnik tehát, hogy az eredetitől különböző frekvenciájú fotonok kerülnek a térbe,
mégpedig a tűsugárzás szempontjából teljesen érthetetlen módon. Természetesen további nehézségek is
lennének ezeket azonban nem részletezzük, mert az eddigiek is mutatják ennek a képnek az elégtelenségét.
A B) alatt említett lehetőséggel éppen a legújabb időben Jánossy Lajos magyar fizikus foglalkozott.
E szerint a fotont »részecskének« kell tekintenünk, azonban hatalmas kiterjedésű
részecskének, amelyet »léggömbhöz« hasonlíthatnánk. Ennek mozgását, belsejének
struktúráját és az anyaggal való kölcsönhatását bonyolult törvényszerűségek szabnák meg, amely
törvényszerűségeket a Maxwell-egyenletek továbbfejlesztésével lehetne megtalálni. Az eddig észlelt
interferencia-kísérletek, ha nem is könnyen, elvileg magyarázhatók lennének. Hiszen ez a foton éppen
nagy kiterjedésénél fogva az interferenciakísérletben szereplő összes tükrökkel, résekkel, stb.
kölcsönhatásban állna és így a »léggömb« alakulását, mozgását azok együttesen szabnák
meg. Abszorbciónál a »léggömb« összeugrik, ez az illető atom és a »léggömb«
belső megfelelő tartományának szerencsés összeilleszkedése esetén következik be. Valamilyen
meghatározott abszorbens esetében ez annál valószínűbb, minél több, a foton számára hozzáférhető
atomot tartalmaz. Ahhoz, hogy a részletes kísérleti ellenőrzést végre lehessen hajtani, szükséges
volna ezt a »módosított részecske« elgondolást kvantitatív formába önteni. Semmi
esetre sem utasítható el azonban ennek hiányában, hiszen láttuk, hogy itt elvi problémáról van szó
és hogy az eddigiekben felsorolt egyszerűbb elképzelések semmi módon nem egyeztethetők össze
a tapasztalattal.

Nézzük meg azonban, hogy milyen elvi nehézségek támaszthatók a fent vázolt
elgondolás ellen. Elsősorban nem lehet tudni, hogy a foton mekkorára tud »dagadni«.
Láttuk, hogy legalább akkora kell, hogy legyen, mint maga az interferencia-berendezés. Az eddigi
legnagyobb méretű berendezéseket véve alapul, legalább 100 m-es nagyságrendet kell feltételeznünk.
Kérdés továbbá, hogy abszorbciónál mi húzza össze a fotont. Az összehúzódásnál c-nél
gyorsabban terjedő hatásokat kell feltételeznünk. Végezetül pedig az elmélet nehezen egyeztethető
össze Joffe kísérletével. Joffe pontszerű röntgenfényforrást állított elő, melynek intenzitását ismerte
és melynek sugarait kondenzátorlapok közé vitt bizmutgolyócskákra engedte.
Ha a γ foton eltalálta a golyócskát, fotoeffektus lépett fel, a golyó töltése megváltozott, amit a
Millikan-kísérlethez hasonló módon észlelni lehetett. Joffe azt találta, hogy
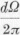 annak valószínűsége,
hogy egy kilépő foton gerjessze a bizmutgolyót, ahol dΩ az a kúpszög, amely alatt a
bizmutrészecske a fényforrástól látszik. A fenti elgondolás szerint ez az eredmény erősen befolyásolható
kellene, hogy legyen olyan módon, hogy a fényforrás mellé, azonban a bizmutgolyóval ellenkező oldalra
nagy kiterjedésű, de teljesen abszorbeáló fekete felületet teszünk. Ez a felület ugyanis sokat elnyelne azok
közül a fotonok közül is, amelyeket egyébként a bizmutgolyó abszorbeált volna. Bár ezt a kísérletet ilyen
értelemben tudomásunk szerint még nem végezték el, egy ilyen várakozás helyessége teljesen
valószínűtlennek látszik. Ismét látjuk tehát, hogy sem az A), sem a B) alatt
felsorolt lehetőségek nem vezetnek célhoz a dilemma megszűntetésében. Ha a foton hullám, akkor igenis
nagy kiterjedést kell neki tulajdonítani, ha részecske, akkor viszont igenis kis golyócskákból áll; más
szóval a részecske és hullámtulajdonságokat szemléletes módon összeolvasztani nem lehet. Azt
viszont már sokszor láttuk, hogy külön-külön egyik sem kielégítő.
annak valószínűsége,
hogy egy kilépő foton gerjessze a bizmutgolyót, ahol dΩ az a kúpszög, amely alatt a
bizmutrészecske a fényforrástól látszik. A fenti elgondolás szerint ez az eredmény erősen befolyásolható
kellene, hogy legyen olyan módon, hogy a fényforrás mellé, azonban a bizmutgolyóval ellenkező oldalra
nagy kiterjedésű, de teljesen abszorbeáló fekete felületet teszünk. Ez a felület ugyanis sokat elnyelne azok
közül a fotonok közül is, amelyeket egyébként a bizmutgolyó abszorbeált volna. Bár ezt a kísérletet ilyen
értelemben tudomásunk szerint még nem végezték el, egy ilyen várakozás helyessége teljesen
valószínűtlennek látszik. Ismét látjuk tehát, hogy sem az A), sem a B) alatt
felsorolt lehetőségek nem vezetnek célhoz a dilemma megszűntetésében. Ha a foton hullám, akkor igenis
nagy kiterjedést kell neki tulajdonítani, ha részecske, akkor viszont igenis kis golyócskákból áll; más
szóval a részecske és hullámtulajdonságokat szemléletes módon összeolvasztani nem lehet. Azt
viszont már sokszor láttuk, hogy külön-külön egyik sem kielégítő.
 A helyzet a lelkiismeretes fizikus előtt valóban kétségbeejtőnek látszik. Mindenekelőtt kiemelendő azonban
a következő alapvető jelentőségű tény: Vannak kísérletek, amelyek a részecskeképpel megmagyarázhatók,
hullámképpel nem, és vannak olyan kísérletek, amelyeknél fordított a helyzet. De nincsen olyan kísérlet,
amely a részecske-természetet teljesen igényelné, amelyben a fénykvantum a részecske fogalmát teljesen
kimerítené, azt teljességében bizonyítaná, és nincs olyan kísérlet sem, egyetlen egy sem, amely a
hullámtermészetet igényelné teljesen, azt bizonyítaná. Valóban, hogy csak egy példát említsünk, azokban
a kísérletekben, amelyekben a foton abszorbcióját, mint kis helyre lokalizált processzust, (mint a
foton »becsapódását«) észlelhetjük, soha. nem adhatjuk meg egyszersmind a fotonnak,
mint részecskének a pályáját is. Hiszen adott
kísérleti berendezés mellett (lásd ábra) lehetetlenség választ adni arra a kérdésre, hogy melyik nyíláson jött á
t a foton.*
A helyzet a lelkiismeretes fizikus előtt valóban kétségbeejtőnek látszik. Mindenekelőtt kiemelendő azonban
a következő alapvető jelentőségű tény: Vannak kísérletek, amelyek a részecskeképpel megmagyarázhatók,
hullámképpel nem, és vannak olyan kísérletek, amelyeknél fordított a helyzet. De nincsen olyan kísérlet,
amely a részecske-természetet teljesen igényelné, amelyben a fénykvantum a részecske fogalmát teljesen
kimerítené, azt teljességében bizonyítaná, és nincs olyan kísérlet sem, egyetlen egy sem, amely a
hullámtermészetet igényelné teljesen, azt bizonyítaná. Valóban, hogy csak egy példát említsünk, azokban
a kísérletekben, amelyekben a foton abszorbcióját, mint kis helyre lokalizált processzust, (mint a
foton »becsapódását«) észlelhetjük, soha. nem adhatjuk meg egyszersmind a fotonnak,
mint részecskének a pályáját is. Hiszen adott
kísérleti berendezés mellett (lásd ábra) lehetetlenség választ adni arra a kérdésre, hogy melyik nyíláson jött á
t a foton.*
Éppen ellenkezőleg. Az eddigiekben felsorolt eredmények meggyőzően bizonyítják, hogy a fény nem állhat
sem részecskékből, sem pedig valamely közeg által hordozott hullámokból. A kiutat éppen az a radikális
felismerés szolgáltatja, hogy a fény természetét nem lehet a makroszkopikus tapasztalatokból absztrahált
szemléleti elemek segítségével megérteni. El kell fogadnunk, hogy a fény jelenléte magának a térnek valamiféle
gerjesztett állapotát jelenti. A fény tulajdonságaival magát a teret kell felruháznunk.
Ez a felfogás nem lesz olyan idegen, ha az előbbiekre gondolva belátjuk, hogy más kiút csakugyan
nincsen, másrészt pedig ha eszünkbe idézzük, hogy az éterfogalom likvidálása után maga a klasszikus
Maxwell-elmélet sem más, mint térelmélet. (Amely azonban természetesen éppen a kvantumjelenségeket
nem tudja helyesen leírni.) Hogy az »üres« teret bizonyos fizikai tulajdonságokkal kell
felruházni, azt pl. már az égitestek egymásra gyakorolt gravitációs hatása is mutatja, amely hatás
szintén az »üres« téren keresztül továbbítódik. Nos, a modern fizika tapasztalatai arra
utalnak, hogy a térnek nagyonis reális fizikai tulajdonságai vannak és éppenséggel döntő szerepe van
a jelenségek megértésénél.
 Az első kísérlet, amely ezen a nyomon indul el, amely tehát lemond a szemléletes képről és elveti mind a
konkrét részecskeképet, mind a hullámképet, viszont a részleges hullám- és részecsketulajdonságokat
egyesíti, Bohr, Kramers és Slater próbálkozása. Elgondolásukat csak egészen röviden említjük meg.
Állításuk összefoglalva: nincs is »foton», úgyszólván semmi sincs, amit fénynek lehetne
nevezni, csak az anyagot és az azon végbemenő változásokat észleljük. Pl. a fényemisszió és abszorbció
jelenségét a következőképpen kell elképzelni: Az 1-es »lámpa melegíti a teret«, gerjeszti,
pl. olyan módon, hogy gerjesztett atomjai alapállapotba esnek le. A 2-es abszorbens viszont elnyeli az
így felszabadult energiát olyan módon, hogy statisztikusan ugyanannyi atomja alapállapotból gerjesztett
állapotba kerül. Az egyes elemi processzusokra nem is igaz az energia- és impulzus-tétel, azonban
makroszkopikusan, mint statisztikai törvényszerűség, tekintettel az elemi processzusok nagy számára,
kiadódik. A térnek tehát csak virtuális szerepe van. Ezt a virtuális gerjesztettséget a klasszikus hullámok
írják le, amelyek valószínűségi jellegűek: Ahol nagy az amplitudó, ott valószínű az egyes processzusok
bekövetkezése (az utóbbiak felelnek meg a részecske-tulajdonságoknak, míg a valószínűségi hullámoknak
viselkedését, mint említettük, a hullámegyenletek írják le, t. i. a Maxwell-egyenletek). A következő évben
azonban Bothe és Geiger koincidencia-berendezés segítségével bebizonyította, hogy a
Compton-effektusnál az energia- és impulzus-megmaradás elve az egyes elemi processzusokon
belül is igaz. Ezzel a fent leírt elméletet megcáfolta. Azóta számos egyéb pontos mérés is bizonyítja,
hogy az említett megmaradási elvek a,z elemi folyamatokra is érvényesek.
Az első kísérlet, amely ezen a nyomon indul el, amely tehát lemond a szemléletes képről és elveti mind a
konkrét részecskeképet, mind a hullámképet, viszont a részleges hullám- és részecsketulajdonságokat
egyesíti, Bohr, Kramers és Slater próbálkozása. Elgondolásukat csak egészen röviden említjük meg.
Állításuk összefoglalva: nincs is »foton», úgyszólván semmi sincs, amit fénynek lehetne
nevezni, csak az anyagot és az azon végbemenő változásokat észleljük. Pl. a fényemisszió és abszorbció
jelenségét a következőképpen kell elképzelni: Az 1-es »lámpa melegíti a teret«, gerjeszti,
pl. olyan módon, hogy gerjesztett atomjai alapállapotba esnek le. A 2-es abszorbens viszont elnyeli az
így felszabadult energiát olyan módon, hogy statisztikusan ugyanannyi atomja alapállapotból gerjesztett
állapotba kerül. Az egyes elemi processzusokra nem is igaz az energia- és impulzus-tétel, azonban
makroszkopikusan, mint statisztikai törvényszerűség, tekintettel az elemi processzusok nagy számára,
kiadódik. A térnek tehát csak virtuális szerepe van. Ezt a virtuális gerjesztettséget a klasszikus hullámok
írják le, amelyek valószínűségi jellegűek: Ahol nagy az amplitudó, ott valószínű az egyes processzusok
bekövetkezése (az utóbbiak felelnek meg a részecske-tulajdonságoknak, míg a valószínűségi hullámoknak
viselkedését, mint említettük, a hullámegyenletek írják le, t. i. a Maxwell-egyenletek). A következő évben
azonban Bothe és Geiger koincidencia-berendezés segítségével bebizonyította, hogy a
Compton-effektusnál az energia- és impulzus-megmaradás elve az egyes elemi processzusokon
belül is igaz. Ezzel a fent leírt elméletet megcáfolta. Azóta számos egyéb pontos mérés is bizonyítja,
hogy az említett megmaradási elvek a,z elemi folyamatokra is érvényesek.
Ebből tehát következik, hogy mégis van értelme fotonról beszélni. A fotonok az energia- és
impulzus-kvantumok »megszemélyesítői«. Van értelme azt mondani, hogy ha egy atom
az E1 energiájú állapotból az E2 energiájú állapotba
esett le, akkor egy hv = E1- E2 energiájú
foton került a térbe; ha egy másik atom az E2 nívóról az
El-re emelkedik fel, akkor egy
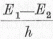 frekvenciájú foton eltűnt a térből.
Erre a folyamatra azt mondhatom, hogy az egyik atom emittált egy fotont, a másik elnyelte és ez a
kijelentés bizonyos mértékig megfelel pl. annak a régebbi naiv kijelentésnek, hogy az egyik atom
kibocsátott egy golyócskát, amely elrepült a másik atomig és ott elnyelődött. Megfelel pedig annyiban,
hogy most is igaz az energia- és impulzus-megmaradás elve éppen úgy, mint a naiv modell esetében,
mélyebb értelmet nyer azonban ez a kijelentés annyiban, hogy kimondásakor arra gondolunk, hogy
emissziónál a tér hv energiával gerjesztett állapotba kerül, az abszorpciónál ez a gerjesztettség megszűnik.
Ha az első atom »2 fotont« bocsát ki, az egyszerűen annyit jelent, hogy a tér kétszer hv
energiával, tehát magasabban lesz gerjesztve.
frekvenciájú foton eltűnt a térből.
Erre a folyamatra azt mondhatom, hogy az egyik atom emittált egy fotont, a másik elnyelte és ez a
kijelentés bizonyos mértékig megfelel pl. annak a régebbi naiv kijelentésnek, hogy az egyik atom
kibocsátott egy golyócskát, amely elrepült a másik atomig és ott elnyelődött. Megfelel pedig annyiban,
hogy most is igaz az energia- és impulzus-megmaradás elve éppen úgy, mint a naiv modell esetében,
mélyebb értelmet nyer azonban ez a kijelentés annyiban, hogy kimondásakor arra gondolunk, hogy
emissziónál a tér hv energiával gerjesztett állapotba kerül, az abszorpciónál ez a gerjesztettség megszűnik.
Ha az első atom »2 fotont« bocsát ki, az egyszerűen annyit jelent, hogy a tér kétszer hv
energiával, tehát magasabban lesz gerjesztve.
A fotonnak ez a most felvázolt fogalma természetesen csak akkor telik meg igazán tartalommal, ha
megtaláljuk azt a matematikai apparátust, amely leírja az elektromágnesség, a fény tulajdonságait hordozó
tér viselkedését, másszóval ha felépítjük a tér kvantumelméletét. Ebben a matematikai apparátusban
a fotonok konkrét, matematikai megfelelői szabatosan megadhatók. Foglaljuk tehát röviden össze,
hogyan indulunk el a sugárzás kvantumelméletében. Az alapelv ismeretes a pontkvantummechanikából.
A klasszikus egyenletekből indulunk ki, azonban bennük azokat a mennyiségeket, amelyeket a
klasszikus elméletben, amint az idő függvényét kerestük, (pl. a részecskék koordinátái) most a
kvantumelméletnek megfelelően átértelmezzük, operátorokat rendelünk hozzájuk, és azokkal számolunk
tovább. Azok a függvények, amelyekre ezek az operátorok hatnak, hivatottak leírni a rendszer
lehetséges állapotait. Minden operátorhoz tartoznak speciális, ú. n. sajátfüggvények, illetve az
ezekhez hozzárendelt sajátállapotok. Tekintsük például az energia operátorát. Ha a kvantummechanikai
rendszer állapota ennek sajátállapota, az annyit jelent, hogy az energia ebben az állapotban egy
bizonyos meghatározott értéket vesz fel. Nos, a sugárzás problémájánál szintén a klasszikus
egyenletekből indulunk ki, amelyek pl. anyagtól mentes elektromágneses tér esetén így hangzanak:
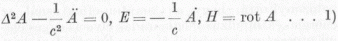 ahol az A a vektorpotenciál, E és H az elektromos illetve
mágneses térerősség. Az eljárás a következő: valamilyen alkalmasan választott ortogonális
A1 (x, y, z), A2 (x, y, z,) ... Ak (x, y, z), ...
függvényrendszer szerint kifejtjük az A vektorpotenciált:
ahol az A a vektorpotenciál, E és H az elektromos illetve
mágneses térerősség. Az eljárás a következő: valamilyen alkalmasan választott ortogonális
A1 (x, y, z), A2 (x, y, z,) ... Ak (x, y, z), ...
függvényrendszer szerint kifejtjük az A vektorpotenciált: 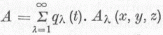 ahol az Aλ-kat bizonyos feltételektől eltekintve szabadon
választhatjuk, természetesen úgy, hogy valóban minden függvény az Aλ-k
szerint haladó sorba legyen fejthető. A matematikából ismeretes, hogy pl. megfelel az
ahol az Aλ-kat bizonyos feltételektől eltekintve szabadon
választhatjuk, természetesen úgy, hogy valóban minden függvény az Aλ-k
szerint haladó sorba legyen fejthető. A matematikából ismeretes, hogy pl. megfelel az
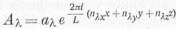 választás, ahol aλ egy konstans vektor,
nλx, nλy, nλz
egész számok, L pedig a térnek nagysága (matematikai okokból a teret végesnek, bár igen
nagynak tekintjük. L természetesen a számítás végén kiesik). Egyébként rögtön látszik, hogy
ezek az Aλ-k éppen a különböző
(nλx, nλy, nλz)
irányvektorok által meghatározott irányokban haladó síkhullámoknak felelnek meg. (Olyan értelemben
tudniillik, hogy ha klasszikusan számolnánk tovább, akkor az 1) egyenleteket éppen a
qλ(t) = e-ivλt
helyettesítéssel lehetne kielégíteni,
ahol
választás, ahol aλ egy konstans vektor,
nλx, nλy, nλz
egész számok, L pedig a térnek nagysága (matematikai okokból a teret végesnek, bár igen
nagynak tekintjük. L természetesen a számítás végén kiesik). Egyébként rögtön látszik, hogy
ezek az Aλ-k éppen a különböző
(nλx, nλy, nλz)
irányvektorok által meghatározott irányokban haladó síkhullámoknak felelnek meg. (Olyan értelemben
tudniillik, hogy ha klasszikusan számolnánk tovább, akkor az 1) egyenleteket éppen a
qλ(t) = e-ivλt
helyettesítéssel lehetne kielégíteni,
ahol 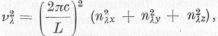 , már pedig
, már pedig
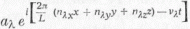 kifejezés pontosan
egy említett irányú síkhullámot ábrázol.) Azonban hangsúlyozzuk, lehetne sok másféle módon is
megválasztani az Aλ-kat a sorfejtéshez. Erre a kérdésre a későbbiekben
még visszatérünk, de már itt leszögezzük, hogy a számítások végeredménye az Aλ-k
speciális választásától független.) A qλ(t) ismeretlen függvények
mármost itt pontosan úgy szerepelnek, mint az ismeretlen koordináták a pontkvantumelméletben.
Rájuk alkalmazzuk tehát az ottani szabályokat. Részletekbe nem megyünk, csak annyit emelünk ki:
Ebben az apparátusban a fotonok úgy jelennek meg, mint az egyes parciális hullámok. Az egyes
qλ-k »nagysága« (kvantummechanikailag átértelmezve)
szabja meg, hogy az illető parciális hullámnak megfelelő fotonból »hány« van jelen, helyesebben,
hogy a tér ilyen formájú gerjesztése milyen fokú, mennyire erős. Ezt precízebben is megfogalmazzuk.
Gondolatban írjuk fel a sugárzó tér energia-operátorát, (tekintsünk el egyelőre az elektromágneses tér
és az ebben levő anyagi részecskék kölcsönhatásától, akkor az energia egyszerűen a térenergiának és
a részecskék energiájának az összege és a nekik megfelelő operátorok is egyszerűen összeadódnak),
és nézzük meg, hogyan és mivel tudjuk jellemezni ennek sajátállapotait. Ismeretes, hogy például a
közönséges kvantumelméletben a hidrogénatom sajátállapotait 3 kvantumszámmal (nlm) lehet jellemezni,
amelyek mindegyikéhez bizonyos »viszonylag szemléletes« jelentést lehet fűzni.
kifejezés pontosan
egy említett irányú síkhullámot ábrázol.) Azonban hangsúlyozzuk, lehetne sok másféle módon is
megválasztani az Aλ-kat a sorfejtéshez. Erre a kérdésre a későbbiekben
még visszatérünk, de már itt leszögezzük, hogy a számítások végeredménye az Aλ-k
speciális választásától független.) A qλ(t) ismeretlen függvények
mármost itt pontosan úgy szerepelnek, mint az ismeretlen koordináták a pontkvantumelméletben.
Rájuk alkalmazzuk tehát az ottani szabályokat. Részletekbe nem megyünk, csak annyit emelünk ki:
Ebben az apparátusban a fotonok úgy jelennek meg, mint az egyes parciális hullámok. Az egyes
qλ-k »nagysága« (kvantummechanikailag átértelmezve)
szabja meg, hogy az illető parciális hullámnak megfelelő fotonból »hány« van jelen, helyesebben,
hogy a tér ilyen formájú gerjesztése milyen fokú, mennyire erős. Ezt precízebben is megfogalmazzuk.
Gondolatban írjuk fel a sugárzó tér energia-operátorát, (tekintsünk el egyelőre az elektromágneses tér
és az ebben levő anyagi részecskék kölcsönhatásától, akkor az energia egyszerűen a térenergiának és
a részecskék energiájának az összege és a nekik megfelelő operátorok is egyszerűen összeadódnak),
és nézzük meg, hogyan és mivel tudjuk jellemezni ennek sajátállapotait. Ismeretes, hogy például a
közönséges kvantumelméletben a hidrogénatom sajátállapotait 3 kvantumszámmal (nlm) lehet jellemezni,
amelyek mindegyikéhez bizonyos »viszonylag szemléletes« jelentést lehet fűzni.
A helyzet itt is hasonló. A térnek és a benne lévő anyagnak egy meghatározott energiaértékhez tartozó
állapotát kvantumszámoknak egy meghatározott sorozatával lehet jellemezni. Ezek között szerepelnek
először is a térben jelenlévő atomok kvantumszámai (éspedig ezek az atomok éppen az ezen
kvantumszámoknak megfelelő energiaértékekkel járulnak hozzá az összenergiához). Továbbá minden
Aλ parciális hullámhoz, fotonhoz tartozik egy kvantumszám, ezt
az illető parciális hullámhoz tartozó betöltési számnak nevezhetjük, mely csak egészszámú értékeket
vehet fel, éspedig, ha értéke nλ akkor ennek a parciális hullámnak
adaléka az összenergiához nλhvλ.
(Mindennek levezetésére itt nem térhetünk ki.) Éppen ez indokolja a betöltési szám nevet, mert hiszen azt
mondhatjuk, hogy hvλ energiájú fotonból éppen nλ
db. van jelen. Sőt éppen ebből látszik, hogy miért feleltetjük meg a »fotonoknak«, vagyis
a fény energia-impulzus kvantumainak éppen ezeket a parciális hullámokat. Másrészt viszont
minden tulajdonság, amivel a fotont felruházhatjuk, ebben az apparátusban benne van. Láthatjuk pl.
hogy ha valamely nλ = 2, ez valóban pusztán annyit jelent, hogy
a térnek Aλ-val jellemzett rezgés-formája kétszeres energiával
van gerjesztve és aligha volna értelme a két fotont valamilyen módon különválasztani. A fotonokhoz
nem lehet az individuális lét fogalmát a naiv szemléletnek megfelelő módon hozzákapcsolni. Ez
nyilvánul meg abban a tényben is, melyet már említettünk, hogy az Aλ-kat,
tehát az egyes parciális hullámokat, az egyes fotonokat, bizonyos önkénnyel választhatjuk meg.
(Matematikailag egy másik választásra való áttérés egyszerűen egy kanonikus transzformációt jelent.)
Láthatjuk tehát, hogy a foton szót hallva a tér gerjesztett állapotára kell gondolnunk, a fotonok
»száma« a gerjesztés fokát jelenti, a fotonok »helyének« vagy
»alakjának« közvetlen fizikai jelentése nincsen.
Nem mehetünk bele a kvantumelektrodinamika további részleteibe. A sugárzás kvantumelmélete
teljesítőképességét illetően messzemenően igazolta a várakozást. Nehézségek természetesen vannak,
azonban nincsen olyan elmélet, amely ne ismerne megoldatlan problémákat.
Noha tulajdonképpen eljutottunk oda, hogy mit kell körülbelül »foton« alatt érteni a fizika
jelenlegi stádiumában, még részletesebben meg kell, hogy nézzük, hogyan kapcsolódik a fotonnak
most már egzakt fogalma a tárgyalás első felében felhozott szemléletesebb leírásmódokhoz. Hol és
hogyan mutatkoznak meg a részecske- és hullámtulajdonságok és hogyan kell nézni a kvantumelektrodinamika
szemszögéből a felsorolt kísérleteket. Először is leszögezzük, hogy azok a korpuszkuláris tulajdonságok,
melyek önkényes szemléleti elemek hozzáfűzése nélkül valóban megfigyelhetők, lényegében egyszerűen
az impulzus és energia kvantumos kicserélését, illetőleg ezzel párhuzamosan az energia-impulzus
tételnek az egyes elemi processzusokra való érvényességét jelentik. Ezek és csakis ezek a korp.
tulajdonságok valóban közvetlenül kiadódnak az elméletből. Nézzünk egy pár tipikus példát, először
a fényemisszió jelenségét. A kvantumelektrodinamika eljárása a következő: Abból a kezdő állapotból
indulunk ki, hogy a sugárzó térben egyetlen gerjesztett atom (mondjuk hidrogén atom) van jelen,
nlm kvantumszámokkal jellemezve. A továbbiakban egyszerűség kedvéért egyetlen
»a« betűvel fogjuk összefoglalva jelölni ezt a három kvantumszámot.
Foton nincs jelen a térben: Az összes nλ betöltési szám a 0 értéket veszi
fel. A fent említett
jelölésmóddal élve, az egész rendszer állapotát az a, 0, 0, 0... sorozat jellemzi. Ezek után (a számítást nem
részletezzük) felírjuk az atom és a sugárzó tér kölcsönhatásának kvantummechanikai kifejezését, és ismert
módon mint perturbációt vesszük tekintetbe. Ismeretes, hogy ez a perturbáció átmeneteket létesít a
kezdeti állapotból más állapotokba. Minden átmenetnek ki tudjuk számítani a valószínűségét. A számítás
szerint 0-tól különböző valószínűséggel csak olyan állapotokba történik átmenet, amelyekben az atom
nincs többé gerjesztett állapotban, ellenben a térben egyetlen foton van jelen éspedig éppen egy olyan,
amely az atom eltűnt energiáját képviseli. Egy ilyen állapot a b, 0, 0, ..., 1λ, 0, 0, ...
sorozattal jellemezhető, ahol a b-ben az atom gerjesztetlen állapotának kvantumszámai vannak összefoglalva.
Az energiamegmaradás pedig az Ea - Eb = hvλ
egyenlettel fejezhető ki.
A megfordított folyamatnál az abszorbciónál a kezdeti állapot valamilyen b, 0, 0, ..., 1λ,
0, 0, ... állapot, a végállapot a, 0, 0, 0, ... Ha a kiinduló helyzet az, hogy a térben jelen van egy foton
és több atom gerjesztetlen állapotban, akkor a számítás minden további nehézség nélkül kiadja
azt, hogy átmenet csak olyan állapotba lehetséges, amelyben a foton eltűnik és az egyik, de csak egyetlen
atom gerjesztett állapotba kerül. Azonnal érthetővé válik tehát, hogy miért nem lehetett a foton
»becsapódását« két különböző helyen észlelni egyszerre, más szóval, hogy miért
nem lehetett a fotont »feldarabolni».
Sőt ezen túlmenőleg érthetővé válik maga az a tény, hogy miért abszorbeálódnak a fotonok egy
atomra koncentrálódva, »becsapódás« formájában. Ami mármost azokat a jelenségeket
illeti, amelyek a fény hullámtermészetére utalnak, ezekre nézve részletezés nélkül megjegyezzük, hogy ezek a
tulajdonságok magukba az (Aλ) parciális hullámokba olvadnak be az
elméletben.
Eddig elintéztük az »objektív korpuszkuláris tulajdonságokat» és ezzel kapcsolatban láttuk,
hogy a fotonok elsőlegesen, egzaktul, bár nem szemléletesen, egyszerűen a térenergia és impulzus kvantált
voltának megjelenítői. A gyakorlatban azonban az a helyzet, hogy sok kísérletet a közvetlen tapasztalaton
túlmenő képekkel teszünk a magunk számára szemléletessé. Pl. a Compton-effektust mindenki úgy képzeli
el, hogy a foton kis golyó módjára ütközést szenved az elektronon és irányt változtatva halad tovább,
csökkent impulzussal. Természetes, hogy az ilyen elképzelések egzakt megfelelőit Már nem találhatjuk
meg a kvantumelektrodinamikában. Esetről-esetre lehetséges azonban a számítást úgy vezetni,
hogy annak menete a szemléletes elképzeléshez simuljon, annak megfeleljen. Így pl. célszerű
épen a Compton-effektusnál az Aλ parciális hullámoknak a fentiekben megadott, különböző
irányokba mutató síkhullámokat választani.. Ekkor ugyanis bizonyos szemléletességgel azt lehet
mondani, hogy a különböző fotonok abban különböznek, hogy különböző irányban haladnak. A
számításnál megint abból indulunk ki, hogy egyetlen megadott irányú foton van jelen a térben, és egy
elektron, és kiszámítjuk az átmenet valószínűségét, egy olyan állapotba, melyben ez a foton eltűnt,
(a hozzátartozó betöltési szám 0 lett) és egy másik irányú foton megjelent. Az érdekes a következő:
Ha a számítás pl. azt mutatja, hogy csak olyan fotonok megjelenésének van valószínűsége, melyeknek
»iránya« (ezt, ismételjük az (nλx,
nλy, nλz) vektor szabja meg) az ábrán
kettős nyíllal van feltüntetve, akkor a kísérlet is azt az eredményt

szolgáltatja, hogy egy kis felfogó-ernyőt az elektrontól távol a térben körülhordozva csak akkor észlelünk
becsapódást, ha az ernyő az ábrán felrajzolt helyen van. Ha tehát ebben a számításban az
Aλ parciális hullámokat, a fotonokat síkhullámoknak választjuk,
akkor valóban hozzásimulunk az ütköző golyócska szemléletes képéhez. Erősen hangsúlyozzuk azonban,
hogy a megfeleltetést nem lehet túlzásba vinni és semmiesetre sincs értelme pl. azt a kérdést feltenni, hogy
az Aλ, az egész térben egyenletes amplitudóval kiterjedő síkhullámnak
megfelelő foton »melyik időpillanatban hol tartózkodik« az e-E »pályán«.
Dehát ezek szerint semmit sem lehet lokalizálni a térben? A klasszikus elmélet szerint az atomok véges
hosszúságú hullámvonalakat bocsátanak ki, az ezekben tartalmazott energia c sebességgel halad
a térben. Hogy a fényhatások valóban c sebességgel terjednek, azt sokszorosan igazolta a tapasztalat,
hogyan kell ezt összhangba hozni az egész térre kiterjedő fotonokkal,
Aλ-kkal? Az energia lokalizációja, a fényhatások véges
sebességgel való terjedése valóban kiadódik az elméletből. Ehhez azonban ismét le kell mondanunk,
az objektív tapasztalatokon túlmenő önkényes szemléleti elemekről. A bajt az okozza, ha a következőt
gondoljuk magunk elé pl. az emisszió jelenségénél: A rendszer (atom + sugárzótér) kezdeti állapota az
a, 0, 0,.... állapot. Egy idő múlva a rendszer átment valamilyen b, 0, 0, .... állapotba.
Ugyanis pontosabban megnézve a dolgot, a helyzet az, hogy a rendszer ilyen állapotoknak, amelyek
egymástól abban különböznek, hogy más-más nλ veszi fel az 1 értéket,
szuperpozíciójába ment át. A számításokat ismét nem követhetjük végig, azonban bizonyos
mértékig azt mondhatjuk, hogy ha pl. az ilyen módon gerjesztett tér egy második atomra hat, akkor
a szuperpozicióban szereplő fotonok együttesen hatnak rá. Ilyen módon lehet levezetni a fényhatás
terjedési sebességét és más olyan jelenségeket, amelyek az energia tér- és időbeli lokalizációjával
kapcsolatosak. Ezzel egyúttal »a különböző fotonok interferenciájának« problémáját is
érintjük. Ha a szuperpozicióban szereplő síkhullám-fotonok együttesen hatnak egy további, a térben
elhelyezett atomra, akkor nyugodtan lehet azt mondani, hogy ezek a különböző fotonok interferálnak
egymással.
Az előbbi bekezdés tartalma a következő:
Ha az egyes elemi processzusokat precízen vizsgáljuk, akkor kitűnik, hogy az elektromágneses tér
végeredményben meglehetősen összetett és bonyolult módon viselkedik, melyhez a klasszikus
szemléleti képek csak egyszerű esetben és akkor sem részletekbe menően fűzhetők hozzá; a
kvantumelektrodinamika segítségével ugyan pontosan tárgyalhatók, viszont az itt fellépő fotonok,
mint olyanok, viszonylag másodlagos jelentőségűek. Ugyanezt más szavakkal kifejezve: alig lehet
pontosan megmondani, mit jelent az a kijelentés, hogy egy atom kibocsátott egy fotont, azonban pl.
ha azt kérdezzük, hogy egy adott szóráskísérletben milyen lesz a kiváltott fotoelektronok számának
szögeloszlása, ezt pontosan ki tudjuk számítani.
Befejezésül egy hasonlattal szeretnénk közelebb hozni a fizikai tulajdonságokkal felruházott térnek a
szemlélet számára nehezen hozzáférhető szerepét. (Ez a hasonlat Marx Györgytől származik.) Egy
fénykvantum emisszióját és rákövetkező abszorbcióját a következő »folyamathoz«
fogjuk hasonlítani: Valaki mondjuk Budapesten felad bizonyos pénzösszeget egy szegedi címre és a
címzett megkapja. Ismeretes, hogy a feladott pénz mennyisége csak a legkisebb pénzegység, a
»pénzkvantum« többszöröse lehet. Viszont hiábavaló lenne a kísérlet, a szó szoros
értelmében végigkövetni a kérdéses pénzmennyiség útját a feladótól a címzettig. »Emissziókor«
a pénz beleolvad a takarékpénztár testébe, »Abszorpciókor« ugyanaz a mennyiség kiválik:
igaz a »megmaradás« tétele, azonban meddő próbálkozás volna meglesni, hogyan ugrik
szét egy 10 forintos 2 db 5 forintosra.
Ugyanez a problémakomplexum, amelyet most az elektromágneses tér kvantumelméletével kapcsolatban
ismertettünk, ma sokkal általánosabb körben aktuális az azóta felfedezett számos új részecsketípussal
kapcsolatban. Újabban különösen Blohincev hangoztatja kutatása programmjaként, hogy a részecskék
tulajdonságaival magát a fizikai teret kell felruházni. Ha igaz is, hogy az elemi részek térkvantumelméletében
még elég sok a nehézség az elért eredmények mellett (aminek nagyrészt az az oka, hogy az elemi részek
közt ható erőkről a tapasztalat eddig nem mondott meg eleget) mégis éppen a részecskék egymásba
való átalakulásának lehetősége meggyőzően bizonyítja, hogy valóban ez kell legyen a fejlődés útja.
Károlyházi Frigyes
Eötvös Loránd Tudományegyetem
Fizikai Intézete
________________________
* Ez a példa abból a szempontból érdekes, hogy jól mutatja a hullám- és részecskekép komplementer
voltát. Ugyanabban a kísérletben is felléphetnek hullám- és részecsketulajdonságok egyszerre, azonban
minél inkább fennáll az, hogy a kísérlet a részecskeképet igényli, annál kevesebbet mutat a hullámjellegből.
Ha pl. a fenti ábrán az egyik lyukat betömjük, akkor a fotonhoz sokkal többet lehet hozzáfűzni a pálya
fogalmából, viszont az interferencia megszűnik. Persze a klasszikus mintára elképzelt részecskének
meghatározott pályán való mozgásának fogalma itt sem adódik ki teljesen! Ehhez azt is meg kellene
mondani, hogy mikor ment át a foton a nyíláson. E célból ezt az egy nyílást is csak egy pillanatra
nyitnánk ki s ha az alatt, amíg nyitva volt, átment egy foton, akkor mindenesetre tudjuk, hogy mikor
ment át. Ismeretes azonban, hogy ebben az esetben a foton energiáját nem tudnánk többé megmondani
stb. Némely kísérletben a viszonyok pontos végigkövetése rendkívül nehéz.
 Látjuk tehát, hogy sem a naiv részecske elképzelés, sem a naiv hullám elképzelés nem tudja kielégítően
leírni a fény természetével kapcsolatos tapasztalatokat. A súlyos dilemmából még két kiutat lehet
megpróbálni. A) A naiv hullámképet úgy módosítani, hogy a részecsketulajdonságok is beleférjenek.
B) Ugyanezt megfordítva, a naiv részecskeképet úgy módosítani, hogy a hullámtulajdonságok is
beleférjenek. Az első úttal próbálkozott meg 1905-ben Einstein, a tűsugárzás elméletének felállításával.
Eszerint a fény ugyan valóban elektromágneses hullám, azonban a térben kis hullámcsomagok alakjában
van jelen. Éspedig egy monokromatikus fénynyalábban a frekvencia v, ezeknek a kis
hullámvonulatoknak, hullámcsomagoknak az energiája hv, impulzusa hv/c. Ezeket a
csomókat nevezte Einstein fotonoknak. A fotonok segítségével az előbb említett két jelenség,
t. i. a fényemisszió, abszorbció és a fotoeffektus valóban érthetővé válik, sőt, mint ismeretes, a
kilépő fotoelektronok maximális energiájára vonatkozó Einstein-féle képlet vagy a színképvonalak
frekvenciáját megadó Bohr-féle frekvenciafeltétel kvantitatíve is teljes megegyezésben van a
tapasztalattal. A fotonok impulzusa szintén ellenőrizhető tapasztalatilag. Elsősorban a fénynyomást
kell említenünk, azonban ezt a Maxwell-elmélet is magyarázza. Ezen túlmenőleg azonban Einstein
1917-ben kimutatta, hogy a Maxwell-féle sebességeloszlás izzó gázokban csak akkor stacionárius,
ha az egyes fotonok éppen
Látjuk tehát, hogy sem a naiv részecske elképzelés, sem a naiv hullám elképzelés nem tudja kielégítően
leírni a fény természetével kapcsolatos tapasztalatokat. A súlyos dilemmából még két kiutat lehet
megpróbálni. A) A naiv hullámképet úgy módosítani, hogy a részecsketulajdonságok is beleférjenek.
B) Ugyanezt megfordítva, a naiv részecskeképet úgy módosítani, hogy a hullámtulajdonságok is
beleférjenek. Az első úttal próbálkozott meg 1905-ben Einstein, a tűsugárzás elméletének felállításával.
Eszerint a fény ugyan valóban elektromágneses hullám, azonban a térben kis hullámcsomagok alakjában
van jelen. Éspedig egy monokromatikus fénynyalábban a frekvencia v, ezeknek a kis
hullámvonulatoknak, hullámcsomagoknak az energiája hv, impulzusa hv/c. Ezeket a
csomókat nevezte Einstein fotonoknak. A fotonok segítségével az előbb említett két jelenség,
t. i. a fényemisszió, abszorbció és a fotoeffektus valóban érthetővé válik, sőt, mint ismeretes, a
kilépő fotoelektronok maximális energiájára vonatkozó Einstein-féle képlet vagy a színképvonalak
frekvenciáját megadó Bohr-féle frekvenciafeltétel kvantitatíve is teljes megegyezésben van a
tapasztalattal. A fotonok impulzusa szintén ellenőrizhető tapasztalatilag. Elsősorban a fénynyomást
kell említenünk, azonban ezt a Maxwell-elmélet is magyarázza. Ezen túlmenőleg azonban Einstein
1917-ben kimutatta, hogy a Maxwell-féle sebességeloszlás izzó gázokban csak akkor stacionárius,
ha az egyes fotonok éppen 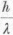 nagyságú impulzussal lökik hátra az atomot, mikor elhagyják.
Nézzük meg azonban, hogy mi a helyzet az interferencia jelenségével.
Kisszögű interferenciánál
a kísérletekre mégcsak találhatnánk magyarázatot e kép alapján. Nem találhattunk azonban magyarázatot
a nagyszögű interferencia-kísérletekre, amelyek közül az első Selényi Pál nevéhez fűződik
(lásd ábra). A P pontból ellentétes irányban kiinduló 1 és 2 fénysugár interferál, ami nem
egyeztethető össze az említett csomagképpel, hiszen a csomag vagy az egyik, vagy a másik ágban
indulna el és nem lehetne jelen egyszerre mindkettőben. Vagy nézzük meg hogyan tudnók magyarázni
az interferenciát a Michelson-féle interferométerben. Mindenekelőtt ismeretes, hogy az interferenciakép
jellege független az intenzitástól, egészen gyenge fény esetén is, ha az egyes csomagok már egyenként
jönnek, változatlan.
nagyságú impulzussal lökik hátra az atomot, mikor elhagyják.
Nézzük meg azonban, hogy mi a helyzet az interferencia jelenségével.
Kisszögű interferenciánál
a kísérletekre mégcsak találhatnánk magyarázatot e kép alapján. Nem találhattunk azonban magyarázatot
a nagyszögű interferencia-kísérletekre, amelyek közül az első Selényi Pál nevéhez fűződik
(lásd ábra). A P pontból ellentétes irányban kiinduló 1 és 2 fénysugár interferál, ami nem
egyeztethető össze az említett csomagképpel, hiszen a csomag vagy az egyik, vagy a másik ágban
indulna el és nem lehetne jelen egyszerre mindkettőben. Vagy nézzük meg hogyan tudnók magyarázni
az interferenciát a Michelson-féle interferométerben. Mindenekelőtt ismeretes, hogy az interferenciakép
jellege független az intenzitástól, egészen gyenge fény esetén is, ha az egyes csomagok már egyenként
jönnek, változatlan.



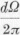 annak valószínűsége,
hogy egy kilépő foton gerjessze a bizmutgolyót, ahol dΩ az a kúpszög, amely alatt a
bizmutrészecske a fényforrástól látszik. A fenti elgondolás szerint ez az eredmény erősen befolyásolható
kellene, hogy legyen olyan módon, hogy a fényforrás mellé, azonban a bizmutgolyóval ellenkező oldalra
nagy kiterjedésű, de teljesen abszorbeáló fekete felületet teszünk. Ez a felület ugyanis sokat elnyelne azok
közül a fotonok közül is, amelyeket egyébként a bizmutgolyó abszorbeált volna. Bár ezt a kísérletet ilyen
értelemben tudomásunk szerint még nem végezték el, egy ilyen várakozás helyessége teljesen
valószínűtlennek látszik. Ismét látjuk tehát, hogy sem az A), sem a B) alatt
felsorolt lehetőségek nem vezetnek célhoz a dilemma megszűntetésében. Ha a foton hullám, akkor igenis
nagy kiterjedést kell neki tulajdonítani, ha részecske, akkor viszont igenis kis golyócskákból áll; más
szóval a részecske és hullámtulajdonságokat szemléletes módon összeolvasztani nem lehet. Azt
viszont már sokszor láttuk, hogy külön-külön egyik sem kielégítő.
annak valószínűsége,
hogy egy kilépő foton gerjessze a bizmutgolyót, ahol dΩ az a kúpszög, amely alatt a
bizmutrészecske a fényforrástól látszik. A fenti elgondolás szerint ez az eredmény erősen befolyásolható
kellene, hogy legyen olyan módon, hogy a fényforrás mellé, azonban a bizmutgolyóval ellenkező oldalra
nagy kiterjedésű, de teljesen abszorbeáló fekete felületet teszünk. Ez a felület ugyanis sokat elnyelne azok
közül a fotonok közül is, amelyeket egyébként a bizmutgolyó abszorbeált volna. Bár ezt a kísérletet ilyen
értelemben tudomásunk szerint még nem végezték el, egy ilyen várakozás helyessége teljesen
valószínűtlennek látszik. Ismét látjuk tehát, hogy sem az A), sem a B) alatt
felsorolt lehetőségek nem vezetnek célhoz a dilemma megszűntetésében. Ha a foton hullám, akkor igenis
nagy kiterjedést kell neki tulajdonítani, ha részecske, akkor viszont igenis kis golyócskákból áll; más
szóval a részecske és hullámtulajdonságokat szemléletes módon összeolvasztani nem lehet. Azt
viszont már sokszor láttuk, hogy külön-külön egyik sem kielégítő.


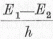 frekvenciájú foton eltűnt a térből.
Erre a folyamatra azt mondhatom, hogy az egyik atom emittált egy fotont, a másik elnyelte és ez a
kijelentés bizonyos mértékig megfelel pl. annak a régebbi naiv kijelentésnek, hogy az egyik atom
kibocsátott egy golyócskát, amely elrepült a másik atomig és ott elnyelődött. Megfelel pedig annyiban,
hogy most is igaz az energia- és impulzus-megmaradás elve éppen úgy, mint a naiv modell esetében,
mélyebb értelmet nyer azonban ez a kijelentés annyiban, hogy kimondásakor arra gondolunk, hogy
emissziónál a tér hv energiával gerjesztett állapotba kerül, az abszorpciónál ez a gerjesztettség megszűnik.
Ha az első atom »2 fotont« bocsát ki, az egyszerűen annyit jelent, hogy a tér kétszer hv
energiával, tehát magasabban lesz gerjesztve.
frekvenciájú foton eltűnt a térből.
Erre a folyamatra azt mondhatom, hogy az egyik atom emittált egy fotont, a másik elnyelte és ez a
kijelentés bizonyos mértékig megfelel pl. annak a régebbi naiv kijelentésnek, hogy az egyik atom
kibocsátott egy golyócskát, amely elrepült a másik atomig és ott elnyelődött. Megfelel pedig annyiban,
hogy most is igaz az energia- és impulzus-megmaradás elve éppen úgy, mint a naiv modell esetében,
mélyebb értelmet nyer azonban ez a kijelentés annyiban, hogy kimondásakor arra gondolunk, hogy
emissziónál a tér hv energiával gerjesztett állapotba kerül, az abszorpciónál ez a gerjesztettség megszűnik.
Ha az első atom »2 fotont« bocsát ki, az egyszerűen annyit jelent, hogy a tér kétszer hv
energiával, tehát magasabban lesz gerjesztve.
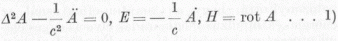 ahol az A a vektorpotenciál, E és H az elektromos illetve
mágneses térerősség. Az eljárás a következő: valamilyen alkalmasan választott ortogonális
A1 (x, y, z), A2 (x, y, z,) ... Ak (x, y, z), ...
függvényrendszer szerint kifejtjük az A vektorpotenciált:
ahol az A a vektorpotenciál, E és H az elektromos illetve
mágneses térerősség. Az eljárás a következő: valamilyen alkalmasan választott ortogonális
A1 (x, y, z), A2 (x, y, z,) ... Ak (x, y, z), ...
függvényrendszer szerint kifejtjük az A vektorpotenciált: 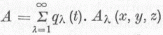 ahol az Aλ-kat bizonyos feltételektől eltekintve szabadon
választhatjuk, természetesen úgy, hogy valóban minden függvény az Aλ-k
szerint haladó sorba legyen fejthető. A matematikából ismeretes, hogy pl. megfelel az
ahol az Aλ-kat bizonyos feltételektől eltekintve szabadon
választhatjuk, természetesen úgy, hogy valóban minden függvény az Aλ-k
szerint haladó sorba legyen fejthető. A matematikából ismeretes, hogy pl. megfelel az
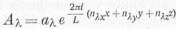 választás, ahol aλ egy konstans vektor,
nλx, nλy, nλz
egész számok, L pedig a térnek nagysága (matematikai okokból a teret végesnek, bár igen
nagynak tekintjük. L természetesen a számítás végén kiesik). Egyébként rögtön látszik, hogy
ezek az Aλ-k éppen a különböző
(nλx, nλy, nλz)
irányvektorok által meghatározott irányokban haladó síkhullámoknak felelnek meg. (Olyan értelemben
tudniillik, hogy ha klasszikusan számolnánk tovább, akkor az 1) egyenleteket éppen a
qλ(t) = e-ivλt
helyettesítéssel lehetne kielégíteni,
ahol
választás, ahol aλ egy konstans vektor,
nλx, nλy, nλz
egész számok, L pedig a térnek nagysága (matematikai okokból a teret végesnek, bár igen
nagynak tekintjük. L természetesen a számítás végén kiesik). Egyébként rögtön látszik, hogy
ezek az Aλ-k éppen a különböző
(nλx, nλy, nλz)
irányvektorok által meghatározott irányokban haladó síkhullámoknak felelnek meg. (Olyan értelemben
tudniillik, hogy ha klasszikusan számolnánk tovább, akkor az 1) egyenleteket éppen a
qλ(t) = e-ivλt
helyettesítéssel lehetne kielégíteni,
ahol 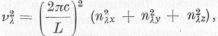 , már pedig
, már pedig
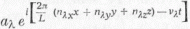 kifejezés pontosan
egy említett irányú síkhullámot ábrázol.) Azonban hangsúlyozzuk, lehetne sok másféle módon is
megválasztani az Aλ-kat a sorfejtéshez. Erre a kérdésre a későbbiekben
még visszatérünk, de már itt leszögezzük, hogy a számítások végeredménye az Aλ-k
speciális választásától független.) A qλ(t) ismeretlen függvények
mármost itt pontosan úgy szerepelnek, mint az ismeretlen koordináták a pontkvantumelméletben.
Rájuk alkalmazzuk tehát az ottani szabályokat. Részletekbe nem megyünk, csak annyit emelünk ki:
Ebben az apparátusban a fotonok úgy jelennek meg, mint az egyes parciális hullámok. Az egyes
qλ-k »nagysága« (kvantummechanikailag átértelmezve)
szabja meg, hogy az illető parciális hullámnak megfelelő fotonból »hány« van jelen, helyesebben,
hogy a tér ilyen formájú gerjesztése milyen fokú, mennyire erős. Ezt precízebben is megfogalmazzuk.
Gondolatban írjuk fel a sugárzó tér energia-operátorát, (tekintsünk el egyelőre az elektromágneses tér
és az ebben levő anyagi részecskék kölcsönhatásától, akkor az energia egyszerűen a térenergiának és
a részecskék energiájának az összege és a nekik megfelelő operátorok is egyszerűen összeadódnak),
és nézzük meg, hogyan és mivel tudjuk jellemezni ennek sajátállapotait. Ismeretes, hogy például a
közönséges kvantumelméletben a hidrogénatom sajátállapotait 3 kvantumszámmal (nlm) lehet jellemezni,
amelyek mindegyikéhez bizonyos »viszonylag szemléletes« jelentést lehet fűzni.
kifejezés pontosan
egy említett irányú síkhullámot ábrázol.) Azonban hangsúlyozzuk, lehetne sok másféle módon is
megválasztani az Aλ-kat a sorfejtéshez. Erre a kérdésre a későbbiekben
még visszatérünk, de már itt leszögezzük, hogy a számítások végeredménye az Aλ-k
speciális választásától független.) A qλ(t) ismeretlen függvények
mármost itt pontosan úgy szerepelnek, mint az ismeretlen koordináták a pontkvantumelméletben.
Rájuk alkalmazzuk tehát az ottani szabályokat. Részletekbe nem megyünk, csak annyit emelünk ki:
Ebben az apparátusban a fotonok úgy jelennek meg, mint az egyes parciális hullámok. Az egyes
qλ-k »nagysága« (kvantummechanikailag átértelmezve)
szabja meg, hogy az illető parciális hullámnak megfelelő fotonból »hány« van jelen, helyesebben,
hogy a tér ilyen formájú gerjesztése milyen fokú, mennyire erős. Ezt precízebben is megfogalmazzuk.
Gondolatban írjuk fel a sugárzó tér energia-operátorát, (tekintsünk el egyelőre az elektromágneses tér
és az ebben levő anyagi részecskék kölcsönhatásától, akkor az energia egyszerűen a térenergiának és
a részecskék energiájának az összege és a nekik megfelelő operátorok is egyszerűen összeadódnak),
és nézzük meg, hogyan és mivel tudjuk jellemezni ennek sajátállapotait. Ismeretes, hogy például a
közönséges kvantumelméletben a hidrogénatom sajátállapotait 3 kvantumszámmal (nlm) lehet jellemezni,
amelyek mindegyikéhez bizonyos »viszonylag szemléletes« jelentést lehet fűzni.