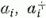SU (2), SU (3), … (második rész)

Györgyi Géza
Központi Fizikai Kutató Intézet

2. Jordan-Wigner-operátorok

A feles spinű részecskék alapvető tulajdonságát ragadja meg a Pauli-féle kizárási elv. Eszerint adott fajta részecske rendelkezésére álló kvantumállapotok mindegyikét legfeljebb egy-egy részecske foglalhatja e1.

Egész spinű részecskék esetében ezzel szemben a részecskeszám adott kvantumállapotban a 0,1, 2, … értékek bármelyikét felveheti. Legyenek 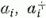az

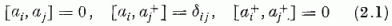
felcserélési összefüggéseket teljesítő operátorok; (2.1)-ből következik, hogy az

operátor sajátértékspektruma: 0, 1, 2 … n_i tekinthető tehát az i jelű kvantumállapothoz rendelt részecskeszám-operátornak.

Feles spinű részecskék esetében Pascual Jordan és Wigner Jenő tűzte ki feladatul - analógiában az előbbiekkel - olyan 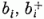operátorok szerkesztését, amelyekből a (2.2) mintára megalkotott

operátor sajátértékei az i jelű kvantumállapothoz tartozó részecskeszám lehetséges értékeit adják.

A Pauli-elv szerint e sajátértékek: 0 és l.

A foton esetében pl. - melynek spinje egész - az 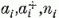operátorok a klasszikus elektrodinamika térmennyiségeiből kiindulva nyerhetők; a kanonikus kvantálás szabályait alkalmazva adódnak a (2.1) csererelációk. A kanonikus kvantálás Heisenberg-Born-Jordan-Dirac-féle módszere tudvalevőleg élesítését képezi a Bohr-féle korrespondencia-elvnek. Ez utóbbi szerint a klasszikus fizika törvényei a megfelelő kvantumfizikai törvényekből a nagy kvantumszámok határesetében állnak elő. A kanonikus kvantálás lehetővé teszi, hogy fordítva is bejárjuk ezt az utat: ismerve a határesetként adódó klasszikus törvényeket, "rekonstruáljuk" a kvantumfizika megfelelő törvényeit. Így nyerhető pl. 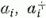a klasszikus elektromágneses térelméletből kiindulva a fotonok viselkedését leíró kvantumelektrodinamika; ennek formalizmusában fellépnek a (2.1)-et teljesítő operátorok, melyekből képezhetők a 0, 1, 2,… sajátértékekkel rendelkező (2.2) részecskeszámoperátorok.

A feles spinű részek, így az elektron esetében, hol a részecskék száma csak a 0,1 értéket veheti fél, a nagy kvantumszámok hiányzanak, klasszikus határeset nincsen, így a kanonikus kvantálás nem alkalmazható. Hasonló a helyzet a spin esetéhez, hol nagy kvantumszámok ugyancsak nincsenek. Klasszikus határeset hiányában az elektronspin kvantummechanikája sem épülhetett ki a kanonikus kvantálás módszerével; azt ehelyett a spinvetület lehetséges értékeire vonatkozó tapasztalatok alapján, a kvantummechanika alapelveire és a forgás csoport tulajdonságaira támaszkodva dolgozták ki. A hasonlóságot fokozza a mindkét esetre jellemző dichotomia; mind az adott kvantumállapothoz tartozó részecskeszám, mind az elektrospin vetülete két értéket vehet fel.

Jordan és Wigner a (2.3)-beli 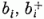Ni operátorok megszerkesztésekor kiaknázta ezt az analógiát. Legyen

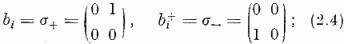
ekkor

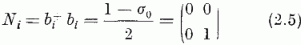
[vö. (1.52)]; fennáll továbbá

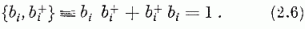
Az i és j jelű, általában különböző kvantumállapotok b, b+ operátoraira (2.6)-ot Jordan és Wigner kézenfekvő módon általánosította:

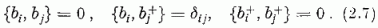
Összevetve (2.7)-et (2.1)-gyel megállapítható: míg az egész spinű részekre a Heisenberg-féle, [,] típusú, "mínusz-jeles" felcserélési összefüggések érvényesek, a feles spinű részecskékre a Jordan-Wigner-féle, { ,} típusú, "plusz-jeles" csererelációknak kell teljesűlniök.

Jelölje a (2.5) alakban előállított N részecskeszám-operátor sajátvektorait ξ₀ és ξ₁ (N, valamint b és b⁺ indexét nem írjuk ki a következőkben). Írható :

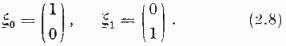
Fennáll:

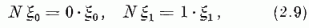
továbbá

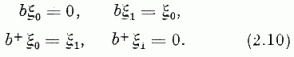
A hasonlóság (1.54) és (2.9-10), valamint (1.2) és (2.8) között szembeötlő. A 0 részecskeszámhoz tartozó ξ₀-t az 1-hez tartozó ξ₁-be transzformáló b⁺-et keltő, a ξ₁-et ξ₀-ba transzformáló b-t elnyelő operátornak mondják.

Az 1/2 spin esetével talált analógia alapján gondolhatnánk arra, hogy a ξ₀, ξ₁ vektorokból tetszőleges c₀, c₁ komplex együtthatókkal képezett c₀ξ₀ + c₁ξ₁ szuperpozíció fizikai jelentése után tudakozódjunk, s hogy olyan operátort vezessünk be, mely - az (1.69)-beli mintájára - mondjuk ξ₀-t ebbe az adott szuperpozícióba transzformálja. Itt azonban véget ér az analógia a spinnel.

A részecskék közönséges, nemrelativisztikus kvantummechanikájában, hol a részecskeszám állandó a mozgás folyamán, valamely szuperpozícióban résztvevő állapotok komplex együtthatói fontos fizikai jelentéssel rendelkeznek. Ennek megvilágítására törekedtünk az 1/2 spin példáján, az (1.69) képlethez kapcsolódó megjegyzéseinkben. A const. részecskeszámmal dolgozó kvantummechanika határain kívül ugyanez érvényes pl. a fotonok esetében a részecskeszám különböző értékeihez tartozó állapotok szuperpozíciójára. (Ilyen szuperpozícióra egy példa a meghatározott fázissal oszcilláló elektromágneses tér.) Más a helyzet, ha egész és feles impulzusmomentumú állapotokat szuperponálunk. Mint Wick, Wightman és Wigner megállapította, ha a φ egész, valamint ψ feles impulzusmomentumú állapotból képezünk formálisan tetszőleges λ, µ komplex együtthatókkal szuperpozíciót, e komplex együtthatók korántsem rendelkeznek a fentiekével analóg "vérbő" fizikai jelentéssel. Pontosabban e szerzők azt mutatták meg, hogy a feltevés, mely szerint a λφ + µψ , valamint λe^iαφ + µe^iβψ szuperpozíciókkal leírt állapotok (α β tetszőleges valós) mérés segítségével megkülönböztethetők volnának, összeférhetetlen a relativisztikus invariancia (az időtükrözés-, ill. elforgatás-operátor létezésének) követelményével. Ténylegesen nem áll rendelkezésünkre semminő (mérési vagy más) módszer, mellyel ezeket a szuperpozíciókat preparálhatnánk vagy egymástól megkülönböztethetnénk. Wick, Wightman és Wigner a tényállás jellemzésére bevezették a szuperkiválasztási elv fogalmát. Azt mondjuk, hogy az egész és a feles impulzusmomentumú állapotok között szuperkiválasztási elv érvényesül.

Alkalmazzuk ezeket a megállapításokat a ξ₀, ξ₁ állapotokra. A 0 részecskeszámhoz tartozó ξ₀ állapot 0 (egész), az 1 feles spinű részecskét tartalmazó ξ₁ állapot feles impulzusmomentumú. Így - ellentétben az 1/2 spin esetével [vö. (1.69)] - a c₀ξ₀ + c₁ξ₁ szuperpozíció komplex c₀, c₁ együtthatóinak fázisai nem nyújtanak semmilyen méréssel nyerhető információt, és nem áll rendelkezésünkre semminő eljárás, mellyel a rendszert a c₀ξ₀ + c₁ξ₁ szuperpozíció leírta állapotba hozhatnánk. Míg tehát az 1/2 spin esetével talált hasonlóság a b, b⁺, N = b⁺b Jordan-Wigner-féle operátorok megszerkesztéséhez igen hasznosnak bizonyult, most látjuk: az analógia nem áll fenn korlátlanul. A korlátozást a szuperkiválasztási elv fejezi ki. Formálisan N és σ₀, b és σ₊, b⁺ és σ_- között találtunk analógiát [vö. (2.4-5)]. Egyaránt fontos fizikai jelentéssel rendelkeznek N és σ₀ = σ₃ sajátértékei és sajátállapotai. 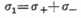A σ₃-éival egyenrangú fizikai jelentése van 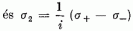sajátértékeinek és -állapotainak; a formális szempontból analóg 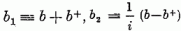, operátorok sajátértékei azonban nem képviselnek fizikai mennyiséget, a megfelelő 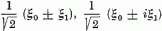sajátállapotok között - megfelelően a szuperkiválasztási elvben megfogalmazott felismerésnek - mérés segítségével különbség nem tehető. Általában a c₀ξ₀ + c₁ξ₁ szuperpozíció c₀, c₁ együtthatóinak fázisai nem tartalmaznak semmilyen méréssel nyerhető információt; így nincs alap itt arra sem, hogy az (1.69)-beli -vel analóg operátort vezessünk be. Az SU (2) generátorok - . mint fent láttuk a Jordan-Wigner-operátorok megszerkesztéséhez igen hasznosaknak bizonyultak; maguknak az SU (2) csoportot alkotó mátrixoknak az alkalmazására azonban itt nem nyílik tér.

3. Az izospin

A neutron felfedezése (Chadwick, 1932) s az annak nyomában született felismerés, mely szerint a neutronok a protonokkal nagyjából egyenrangú alkotóelemei a magoknak, újabb példát mutatott a dichotomiára a kvantumfizikában. Heisenberg javaslatára a protont és a neutront mint a nukleon két különböző állapotát fogjuk fel. A nukleon a helykoordinátáknak és a spinváltozónak megfelelő szabadsági fokok mellett egy további, ötödik szabadsági fokkal is rendelkezik: "tud neutron és tud proton lenni'' .

Legyenek 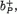, b_P a proton keltő és elnyelő operátorai (adott térbeli mozgásállapotban és spinállapotban), 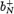és b_N pedig legyenek a megfelelő neutron-keltő és -elnyelő operátorok. Feles spinű részekről lévén szó, ezek az operátorok a (2.7) Jordan-Wigner-csererelációkat teljesítik. A 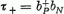operátor az elnyelt neutron helyébe protont kelt, azaz a nukleon neutron-állapotát a proton-állapotba transzformálja; 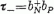viszont a proton-állapotból a neutron-állapotba transzformál. Ezek ketten a 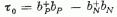operátorral együtt a

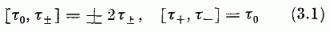
felcserélési összefüggéseket teljesítik. Jelölje a proton állapotvektorát ω_P , a neutronét 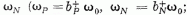a nukleont nem tartalmazó állapot, a vákuum). Írható:

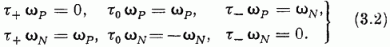
A τ₀ operátor sajátértéke, mely protonra +1, neutronra -1, felfogható, mint a nukleon ötödik szabadsági fokának megfelelő dichotomikus változó. Kiemelendő (3.1) és (1.53), valamint (3.2) és (1.54) formai egyezése. A spinnel fennálló analógiától vezettetve be szokás vezetni a 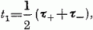, 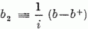operátorokat, melyeket még formálisan összefoglalnak egy t (t₁, t₂, t₃) "vektor"-rá. Fennáll

[vö. (1.55)]; t neve a nukleon izospin-operátora. - Az analógia a spinnel - mely ezen elnevezés bevezetéséhez is az alapot adta - nem érvényes teljesen itt sem. Míg a t₃ operátor, melynek sajátértékei a proton- s a neutron-állapotot különböztetik meg, fizikai jelentéssel rendelkezik, a t₁, t₂ operátoroknak - sajátértékeinek, sajátvektorainak - ilyen jelentés nem tulajdonítható.

Általában valamely c_Pω_P + c_Nω_N szuperpozíció c_P, c_N komplex együtthatóinak fázisai nem rejtenek magukban méréssel nyerhető információt; nem ismerünk eljárást, mellyel a nukleont a megadott szuperpozíció leírta állapotba hozhatnánk. A Wick, Wightman és Wigner által kimondott sejtés szerint a különböző töltésű állapotok, így a proton- és a neutron-állapot között szuperkiválasztási elv érvényesül. Most is megállapítható: a τ₊, τ₀, τ_- SU(2) generátoroknak a nukleonok töltésállapotainak leírásában nagy hasznát vesszük, az SU(2) csoportot alkotó mátrixoknak azonban nem jut hasznos szerep.

Az izospin különösen hasznos eszköz a nukleonrendszerek (magok) s az elemi részek töltésállapotainak rendszerezéséhez. - A mag nukleonjaitól elfoglalt kvantumállapotokhoz tartozó t izospin-operátorokat összegezve nyerjük a mag "eredő'' T = ∑t izospin-operátorát. Abban a közelítésben, amelyben a proton s a neutron tulajdonságai (töltés, tömeg stb.) között fennálló különbség figyelmen kívül hagyható, T felcserélhető a mag energiaoperátorával, T² sajátértéke "jó kvantumszám'' és - Wigner nyomán - a magállapotok jellemzésére használható. Az egymásból egy-egy 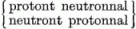helyettesítve nyerhető magállapotok, - a proton s a neutron hasonlósága folytán - hasonló tulajdonságúak; ilyenek alkotják a töltésmultipletteket, melyeket T² sajátértéke (illetőleg az azt meghatározó izospin-kvantumszám) jellemez. A magok töltésmultiplettjeinek, s az atomspektroszkópia spinmultiplettjeinek elmélete között szoros analógia van, mely (3.1) és (1.53) analógiájának folyománya. A magátalakulásokban az izospin-kvantumszám kiválasztási szabályoknak tesz eleget.

Az erős kölcsönhatásokban jelentkező részecskeállapotok is töltésmultiplettekbe rendszerezhetők. Ilyet alkotnak pl. a proton és neutron szimmetrikus kölcsönhatásáért első sorban felelősnek tartott pion + , 0, - töltésű állapotai (triplett) ; a bomláskor nukleont adó rövid élettartamú gerjesztett multiplettek legismertebbje, a Δ kvartett, hosszú élettartamúra pedig a ∑ triplett vagy a Ξ dublett példa. - A megismert és töltésmultiplettekbe sorolt részecskeállapotok száma többszáz. Átfogóbb rendszerezésükhöz - mint később meglátjuk - az SU(3) és az SU(6) nyújt alapot.

4. Kvázispin-operátorok

Még más SU(2) generátorok is képezhetők a proton- és neutron-keltő, valamint elnyelő operátorokból a τ operátorokon (az izospinen) kivül. Legyen 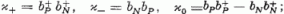ezekre fennáll:

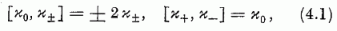
ami (3.1)-gyel és (1.53)-mal alakilag teljesen megegyezik. A κ₊ operátor egy proton-neutron-párt kelt, κ_- azt elnyeli; ha e pár jelen van, κ₀ sajátértéke +1, ha pedig nincs jelen, úgy -1. E κ operátoroknak mindeddig nem vették hasznát a fizikában; mondhatjuk: ez a κ formális játékszer csupán.

Hasznos szerepet kapott azonban ezeknek a κ operátoroknak csaknem betű szerinti mása a szupravezetés elméletében, s méginkább a magelméletben, az ún. szupravezető típusú párkorreláció leírásában. - A szupravezetés leírására Bardeen, Cooper és Schrieffer javasolta

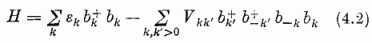
"redukált Hamilton-operátor" kölcsönhatási tagját alkalmazva ≠ 0 eredményt akkor kaphatunk, ha az elektronok párosával foglalják el a -k, k állapotokat (itt a k index az elektron impulzusának és spinvetületének összefoglaló jele; -k az ellentett impulzusú és spinvetületű - időtükrözött - elektronállapotot jelzi); H alapállapota az ilyen párokból felépített sok elektron-állapotok alkalmas szuperpozíciója alakjában kereshető. [A (4.2) képletben b_k, 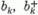a (2.7) összefüggéseket teljesítő Jordan-Wigner-operátorok.] Gyümölcsözőnek bizonyult e Hamilton-operátor a magspektrumok leírásában is (a k index ilyenkor legtöbbnyire az n fő-, az l mellék-, a j belső és az m mágneses kvantumszám összefoglaló jele; -k az n, l, j, -m számnégyest jelzi).

Tegyük fel Bardeen, Cooper és Schrieffer nyomán, hogy (4.2)-ben V_kk, alkalmas átlagértékkel, valamely V állandóval helyettesíthető. Állandónak vesszük ezen kívül (4.2)-ben ε_k-t is: ε_k = ε; ezt megtehetjük, ha V oly nagy, hogy mellette az egyes ε_k-k különbségei elhanyagolhatók ("erős csatolás" határesete), vagy ha a mag bizonyos tulajdonságaiért egyetlen, az n, l, j kvantumszámok rögzített értékével jellemzett szintet elfoglaló nukleonokat kívánunk felelőssé tenni (ebben az esetben a k index m-mel azonosítandó). Az ilyen egyszerűsítéssel nyert

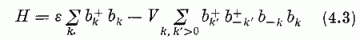
Hamilton-operátor sajátértékfeladata egzaktul megoldható.

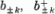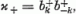
Teljes analógiában a proton- és neutron-állapotok keltő és elnyelő operátoraiból fent képezett κ generátorokkal, képezzük most az adott k-hoz tartozó operátorokból a 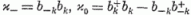operátorokat. Ezek ugyancsak az SU(2) generátorok (4.1) felcserélési összefüggéseit teljesítik. Vezessük be ezen operátorok 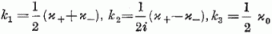kombinációit, melyeket formálisan egy k (k₁, k₂,k₃) .”vektor"-rá foglalunk össze. Fennáll

[vö. (1.55), (3.3)]; k-t kvázispin-operátornak nevezik. Összegezve ezen k, operátorokat a k, -k indexpár különböző (a k index < 0) értékeire nyerjük a 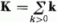"eredő" kvázispin-operátort, melyre (4.4) folyamányaképp

teljesül. Legyen

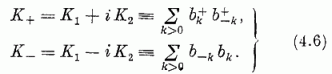
Írható továbbá (2.7), (2.5) alapján:

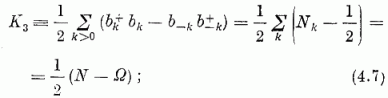
itt 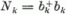a k indexű állapothoz tartozó részecskeszám-operátor, 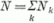a teljes részecskeszám-operátor, 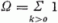a részecskék rendelkezésére álló k, - k állapotpárok száma [feltesszük, hogy Ω véges; pl. a magban a j meghatározott értékével jellemzett szintre helyezett protonok vagy neutronok esetében 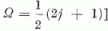. A K operátorokkal kifejezhetjük a (4.3) Hamilton-operátort; a legegyszerűbb H-t és K² és K₃ segítségével előállítani:

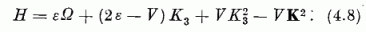
A K₃ operátornak, mint azt (4.7) mutatja, valamely n részecskét tartalmazó állapot sajátállapota az 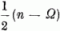sajátérték mellett. Ha valamely, a részecskeszám n értékéhez tartozó állapot sajátállapota még K²-nek, úgy sajátállapota lesz a (4.8) Hamilton-operátornak is.

Legyen η₀ a részecskét nem tartalmazó állapot, a vákuum. Alkalmazzuk erre egyszer, majd kétszer, háromszor, … a K₊ operátort; ilyen módon rendre két-, négy-, hatrészecske-állapotokat sit. nyerünk. - Legyen az így nyert K₊η₀ kétrészecske-állapotra - és egymásra is - ortogonális kétrészecske-állapotok jele η_{2; σ} (a σ index a megkülönböztetésükre szolgál), és alkalmazzuk ezekre is egyszer, majd kétszer, háromszor sit. a K₊ operátor t. - Az így nyert K₊ η_{2; σ} állapotokra, valamint -ra - s egymásra - ortogonális négyrészecske állapotok jele η_{4; σ} lesz; alkalmazzunk ezekre is egyszer, kétszer, háromszor, … a K₊ operátort. Így eljárva az állapotok

rendszerére jutunk. Alkalmazzuk K² = K₊K_- + K₃(K₃-1)-et először η₀-ra. Az elnyelő operátorból felépült K_- alkalmazásakor zérus adódik; K₃(K₃-1) az 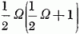tényezővel szoroz. - Ugyancsak zérust kapunk, ha K--t az η2;σ állapotokra alkalmazzuk. Feltettük ugyanis, hogy az η_{2; σ} -k ortogonálisak K₊ η₀-ra: 0 = (η_2;σ, K₊ η₀) = (K_-η_2;σ,η₀); az utóbbi alak K_-η_2;σ és η₀ ortogonalitását állítja, amiből K_-η_2;σ = 0 következik. 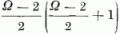A K² operátor alkalmazása így most is K₃(K₃-1)-ével helyettesíthető, s ez az tényezővel való szorzást jelent. - Hasonlóképpen általánosságban igazolható a K_-η_s;σ = 0 összefüggés fennállása, ennek alapján pedig K²-nek η_s;σ-hoz tartozó sajátértékére 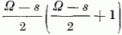adódik (s = 0,2,4, …). A K², K₊ operátorok (4.5) értelmében felcserélhetők. Ennek folytán (4.9) egy-egy sorában K₂-nek egy és ugyanazon sajátértékhez tartozó sajátállapotai állnak. A sajátértéket - mint láttuk - az 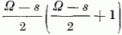kifejezés adja meg, ahol s a Racah bevezette szenioritás; s az a - legkisebb - részecskeszám, amely mellett az adott sajátérték először fellép. Így pl. a 0 szenioritáshoz tartozó állapotok "családfája" egészen a 0 részecskeszámig megy vissza, a 2 szenioritásúaké a 2 részecskeszámig sit. - A K², K₃ operátorok sajátértékeinek 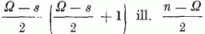kifejezését felhasználva a (4.8) Hamilton-operátor sajátértékére kapjuk:

*

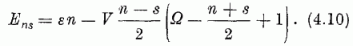
Most is elmondható: az SU(2)generátor kvázispin operátoroknak nagy hasznát vettük; a megfelelő SU(2) csoport alkotó mátrixok azonban itt sern kapnak oly fizikailag tartalmas szerepet, mint az 1/2 spin elméletében. A szupravezető elektronjai s a mag protonjai esetében ezen SU( 2) csoport mátrixainak alkalmazása különböző töltésű állapotok szuperpozícióját eredményezheti; a - töltetlen - neutronok esetében is különböző barionszámú állapotok szuperpozíciója adódhat.

Mint említettük, minden jel arra mutat, hogy a különböző töltésű állapotok között, szuperkiválasztási elv érvényesül; ugyanez a különböző barionszámú állápotokról is elmondható. A szóbanforgó szuperpozíciók komplex amplitudóinak fázisa így fizikailag semmitmondó; a megadott szuperpozíció leírta állapot preparálására nincs módunk. (Megemlítjük, hogy Bardeen, Cooper és Schrieffer mindazonáltal formálisan dolgozott a töltés különböző értékei jellemezte sokelektronállapotok szuperpozíciójával, megjegyezve, hogy a rendszer leírására ennek a szuperpozíciónak a maximális súllyal képviselt részecskeszámhoz tartozó altérre vetett vetületét kell választanunk. Bardeen, Cooper és Schrieffer közelítő módszerének Bogoljubov és Valatin elegáns megfogalmazását adta, felhasználva az SU(2)'csoport valós mátrixait.)

5. A síkbeli izotróp harmonikus oszcillátor vagy az impulzusmomentum kvantumelmélete Schwinger szerint

A síkbeli izotróp harmonikus oszcillátor energiája (a Hamilton-függvény):

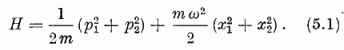
A (kanonikus) mozgásegyenletek:

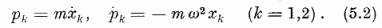
Bevezetve a

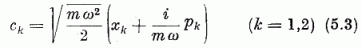
komplex változókat, (5.1) a

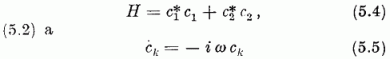
alakba írható. Az (5.5) mozgásegyenletek alapján könnyen látható, hogy a 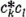szorzatok mind (k, l = 1,2) mozgásállandók. Ha k = l = 1, ill. 2, az x_1^-, valamint az x_2^- tengely mentén végbemenő harmonikus rezgőmozgás energiáját kapjuk; a k ≠ l indexű - komplex - mozgásállandók abszolútértéke az előbbi két energia geometriai középértékével egyenlő, arkuszuk pedig a két oszcilláció fáziskülönbségét szolgáltatja. Képezhetjük a szimmetrikusabb, valós

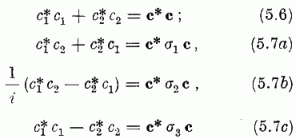
kombinációkat is [itt bevezettük a c₁, c₂ komponensekkel rendelkező c komplex vektort; a σ_r Pauli-mátrixokat (1.22) alatt adtuk meg]. Az (5.6-7) kombinációk jelentése a 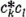-ekéből következik. Közülük (5.6) a Hamilton-függvény (összenergia), (5.7b) az impulzusmomentum ω-szorosa (c* × c = i ω r × p); (5.7c) az x₁- és x₂-tengely, (5.7a) az x2 = x₁ és az x₂ = - x₁ egyenes mentén végzett harmonikus rezgőmozgások energiáinak különbsége. Említésre érdemes e mozgásállandók geometriai értelme. Ezt - elhagyva a közös faktort - az alábbi kis táblázat szemlélteti:

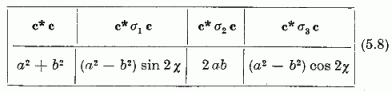
Itt a és b a Lissajous-féle pályaellipszis fél nagy-, ill. kistengelye, χ a nagytengely és a koordinátarendszer x₁-tengelye által közbezárt szög. E mozgásállandók nem mind függetlenek, fennáll közöttük a

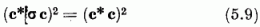
reláció.

Vizsgáljuk a síkbeli izotróp harmonikus rezgőmozgás olyan transzformációit, amelyekkel szemben az energia (a Hamilton-függvény) értéke invariáns. - Kereshetnénk az energia mellett talált, a mozgásra jellemző c*σ_rc (r = 1, 2, 3) állandók azon lineáris transzformációit, amelyek változatlanul hagyják a c*c energiát. Ilyenek (5.9) szerint a c*σc háromkomponensű, valós "vektor"ra, alkalmazott elforgatások (általánosabban ortogonális transzformációk). Vagy kereshetjük maguknak a c kétkomponensű komplex vektoroknak azon

lineáris tránszformációit, amelyek teljesítik az energia invarianciájának c'*c' = c*c feltételét. Ez maga után vonja unitér jellegét [lásd (1.10)]. A mátrixok az U(2) csoportot képezik. Először az utóbbi transzformációkkal foglalkozunk; (5.10) alapján ugyanis az (5.7) mozgásállandók transzformációja egyszerűen meghatározható, míg megfordítva c* σ c transzformációjának ismeretében nem olyan egyszerű c-ére következtetni, mely ekkor nem is egyértelműen meghatározott.

A unitér mátrix determinánsa - tudjuk - egységnyi abszolútértékű [lásd (1.15)]. Így előállítható mint valamely exp iφ tényező s egy unimoduláris unitér mátrix szorzata. Az exp iφ faktor egyöntetűen változtatja meg minden mozgás fázisát (az időtengely kezdőpontját tolja el); a pályaellipszist és a befutás értelmét érintetlenül hagyja. Ha érdeklődésünk csak ezen irányítással ellátott pályaellipszisekre terjed ki, úgy - az U(2) csoportról az SU(2) csoportra szorítkozva - megkövetelhetjük, hogy a mátrix unimoduláris legyen. Az unimoduláris unitér mátrixok - melyek az SU(2) csoportot képezik - kényelmes kifejezését (1.23) alatt adtuk meg. Mint (1.25-28) segítségével megállapítható, ha a c kétkomponensű komplex vektorra az SU(2) csoport (α) mátrixát alkalmazzuk, a háromkomponensű valós c*σc vektor α forgásvektorú elforgatást szenved. A forgásvektor szemléletes jelentését kevés szóval nem könnyű jellemezni. Annak megállapítására szorítkozunk, hogy a (α) mátrix alkalmazása az α(α, 0, 0) esetben az x₂ = x₁ és az x₂ = - x₁ egyenes mentén végbemenő rezgőmozgás között a fáziskülönbséget eredményez, α (0, α, 0) esetén a pályaellipszist elforgatja 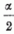szöggel a centruma körül, az α(0,0 α) esetben pedig az x₁- és az x₂-tengely mentén végzett oszcillációk között hoz létre α fáziskülönbséget. Ennek megfelelően e három fajta transzformáció közül az első az x₂ = x₁, valamint az x₂ = - x₁ egyenesbe, a harmadik az x₁-, valamint az x₂- tengelybe első pályákat hagyja változatlanul, a második fajtával szemben pedig minden körpálya invariáns.

Ejtsünk néhány szót az SU(2) csoport s a térbeli elforgatások kapcsolatáról, mellyel elsőízben az elektrospinnel kapcsolatban, és most a síkbeli izotróp harmonikus oszcillátort vizsgálva újból találkoztunk. A spinfüggvények elforgatáskor mutatott transzformációjának [lásd (1.8)] meghatározására törekedve azt találtuk, hogy e transzformációk mátrixai az SU(2) csoportot alkotják és a forgáscsoport kétértékű ábrázolását létesítik. Míg a spin esetében az elforgatásokból kiindulva jutottunk az SU(2) csoporthoz, a síkbeli izotróp harmonikus oszcillátor esetében a c-re alkalmazott SU(2) [ill. U(2)] transzformációk [lásd (5.10)] az elsődlegesek, ezek rendelkeznek közvetlen fizikai jelentéssel; a c-ből leszármaztatott mozgásállandó c*σc "vektor" forgástranszformációi, ill. ezek - valós unimoduláris ortogonális - mátrixai természetszerűen mint ezen SU(2) csoport ábrázolása foghatók fel. Ez a szó szoros értelemében vett, vagyis egyértékű ábrázolás; megjegyzendő azonban, hogy nem hű: az SU(2) csoport két, egymástól előjelben különböző mátrixához ugyanazt a forgástranszformációt (ortogonális mátrixot) rendeli. - Az SU(2) csoportot alkotó mátrixoknak mint a forgáscsoport kétértékű ábrázolásának fellépte az 1/2 spin elméletében, valamint az SU(2) csoport forgástranszformációs mátrixok létesítette ábrázolásának jelentkezése a síkbeli izotróp harmonikus oszcillátor esetében az SU(2), valamint a forgáscsoport - vagy a valós unimoduláris ortogonális mátrixok csoportja, az SO(3) csoport - szerkezete között fennálló benső rokonsággal van kapcsolatban. Ez a rokonság: a két csoport elemei között kettő-egy-értelmű művelettartó megfeleltetés létesítésének lehetősége, másképpen: kettő-egy homomorfia.

Megjegyezzük még, hogy (5.10) kanonikus transzformáció. Az (5.10) transzformációs képlet és komplex-konjugáltja a W (c, c' * ) = c' * c alkotófüggyvényből a c' = δW/δc'*, c* = δW/δc módon származtatható. A transzformáció

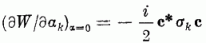
infinitezimális generátorai a 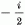faktortól eltekintve éppen az (5.7) mozgásállandók.

*

A klasszikus mechanika keretei között fent mondottak, a kvantummechanikában kevés változtatással elismételhetők. A Hamilton-operátort mint p_k és x_t függvényét (5.1) adja meg; az impulzuskomponensek p_k és a koordináták x_l operátorai a

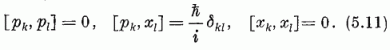
Heisenberg-Born-Jordan-féle felcserélési összefüggéseket tartoznak kielégíteni. Most is bevezethetők az (5.3) kombinációk. A c_k mennyiségek időfüggése - a klasszikus és a kvantummechanikában egyaránt - az (5.5) egyenlet értelmében exp (-iωt) alakú; az amplitúdót 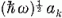alakban írjuk fel: 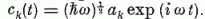ck(t) = ((ħω)½ ak Az a_k nem-hermitikus operátorokra és adjungáltjukra (5.3), (5.11) alapján a

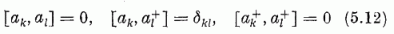
felcserélési összefüggések adódnak [vö.(2.1)]. Az (5.6-7)-tel analóg c⁺c és c⁺ σc most is mozgásállandók, s az a_k, 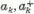amplitúdókkal - ill. az azokat összefoglaló a, a⁺ operátor- vektorokkal - is kifejezhetők. A 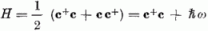Hamilton-operátor [vö. (5.4-6)] így a

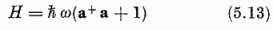
alakot nyeri, az I = (2ħω)^-1 c⁺ σc képlettel értelmezett mozgásállandó "vektor" pedig így írható:

A (5.9) képlet helyett most (c⁺σc)² = (c⁺ c)² +2ħωc⁺c teljesül:

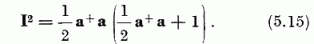
A c operátor-vektor (5.10), vagy a ebből adódó

transzformációjával szemben, hol az U(2) csoport bármely mátrixa lehet, az (5.13) Hamilton-operátor invariáns. Az U(2) csoportról az SU(2)-re szorítkozva, majd felhasználva -nek (1.23) kifejezését, beláthatjuk [vö. (1.25-28]): ha: (α)-t a-ra alkalmazzuk, az I "vektor" α forgásvektorú elfordulást végez, vagy másképpen: I komponensei az SU(2) csoportnak az SO(3) mátrixai létesítette ábrázolása szerint transzformálódnak. Mindez a legszorosabb analógiát mutatja a klasszikus elméletben tett megállapításokkal. - Megemlítjük, még, hogy az (5.16) [vagy (5.10)] transzformáció a kvantummechanikában is kanonikus (azaz hasonlósági) transzformáció:

ahol T mint α függgvénye:

Az exponenciális függvény hatványsorát felhasználva, (5.14) és (5.12) segítségével igazolható (5.17-18) és (5.16), (1.23) azonossága. Fennáll

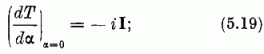
az (5.17-18) kanonikus transzformációkat az I₁, I₂, I₃ mozgásállandók generálják. Feljegyezzük még (5.14), (5.12) alapján I (I₁, I2, I₃) felcserélési összefüggéseit:

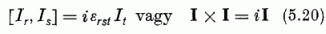
[vö. (1.43-46), (1.55-56), (3.3), (4.4-5)]. A párhuzam a klasszikus és a kvantumelmélet között még itt is fennáll; ha úgy tetszik az (5.20)-szal [akárcsak az (5.11-12)-vel] analóg klasszikus Poisson-zárójeles összefüggések is felírhatók.

*

A mozgásállandók (5.8) geometriai jelentése s az SU(2) transzformációk szemléletes értelmezése - a pályaforgalom alkalmazhatóságának ismert korlátai folyományaképpen - természetesen nem (ill. csak a nagy kvantumszámok határesetében) vihető át a klasszikus tárgyalásból a kvantummechanikába. Oktalanság volna azonban fájlalni ezt a "veszteséget", nyomban látni fogjuk, hogy a kvantummechanikában mennyivel gazdagabb bőségben adódnak a Hamilton-operátor invarianciájának következményei, mint a klasszikus mechanikában.

A pályafogalom (és a klasszikus mozgás időbeli lefolyása) helyére a kvántummechanikában tudvalevőleg a kvantummechanikai állapot fogalma lép. A síkbeli izotróp harmonikus oszcillátor energiasaját állapotainak teljes ortonormált rendszere felírható a

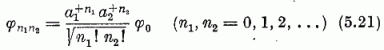
alakban; itt φ₀ ≡ φ₀₀ az alapállapot, melyre a₁φ₀ = a₂φ₀ = 0 . Az (5.12) felcserélési összefüggések segítségével nyerhetők az

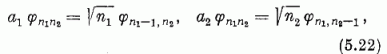
közvetlenül (5.21) alapján pedig az

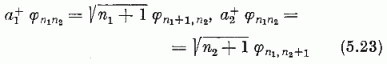
relációk. Mint (5.13), (5.22-23) segítségével megállapítható, φ_n1n2-re a

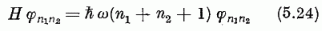
energiasajátértékegyenlet teljesül. Eszerint n_t (i = 1,2) az oszcillátor i indexű szabadsági fokához tartozó ħω energiakvantumok számát jelenti; megfelelően (5.22-23)-nak, 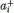neve kvantumkeltő, a_i-é pedig kvantum-elnyelő operátor.

A H Hamilton-operátor az SU(2) csoport (5.16) transzformációval szemben invariáns; (5.17) felhasználásával írható: H = T-¹HT. Ezt (5.24)-be helyettesítve és mindkét oldalra alkalmazva T-t kapjuk:

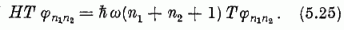
Még itt is fennáll bizonyos analógia a klasszikus elmélettel. Ott azt láttuk: ha a mozgást mint az idő függvényét leíró c komplex vektor-függvényre az SU(2) csoport valamely mátrixát alkalmazzuk [lásd (5.10)], változatlan energiájú mozgást leíró c'-t kapunk. Itt ezt látjuk: ha a φ_n1n2 kvantummechanikai állapotra az SU(2) generátor I generálta T transzformációt [lásd (5.18)] alkalmazzuk, ugyanahhoz az energiasajátértékhez tartozó φ'_n1n2 = T φ_n1n2 sajátállapotot nyerünk.

Mindez érdekes, de így önmagában nem különösen gyümölcsöző. A kvantummechanikában azonban ennél többet mondhatunk. A T φ_n1n2 transzformált állapot előállítható az eredeti φ_n1n2 állapotok lineáris kombinációja alakjában:

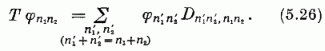
Ha a-t először a (α), majd a (β) transzformációnak vetjük alá: a" = (β) (α) a, s ennek megfelelően φ_n1n2-re először T(α)-t, majd T(β)-t alkalmazzuk, úgy írható:

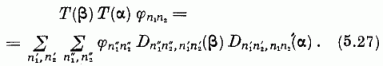
Az SU(2) csoport elemei s az (5.26) lineáris kombinációk együtthatói alkotta 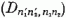mátrixok között fennálló megfeleltetés eszerint a

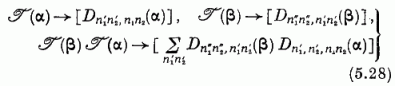
tulajdonságú, művelettartó. A 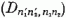mátrixok az SU(2) csoport egy ábrázolását képezik.

A kvantummechanikában - és ennek klasszikus megfelelőjét hiába keresnénk - egy-egy energiaszinthez a H Hamilton-operátort változatlanul hagyó transzformációk csoportjának, másként: H invariancia- (vagy szimmetria-) csoportjának meghatározott ábrázolása tartozik. Az ábrázolás mátrixainak indexei: a kvantumszámok; a mátrixok sorainak vagy oszlopainak száma, vagyis az ábrázolás dimenziója: az elfajulás foka; ismerve az ábrázolást, a kvantumátmenetekre kiválasztási szabályok és intenzitásképletek, adott típusú perturbáció okozta szintfelhasadásra intervallum-szabályok - azaz egész sereg fontos fizikai eredmény - nyerhető.

Képezve az (5.14) generátor "vektor" komponenseinek I_± = I₁ ± i I₂ kombinációit, írható:

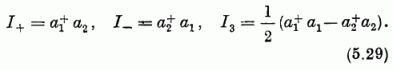
Ezek (5.22-23) szerint így hatnak a φ_n1n2; állapotokra :

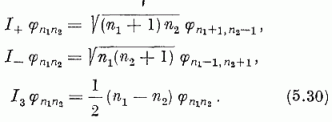
Az (5.19), (5.26) képletek segítségével innen a fent talált ábrázolások (δ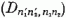(a)/δa_r)_α=0 (r = 1, 2, 3) infinitezimális mátrixai leolvashatók. Lie szerint az infinitezimális mátrixok ismeretében az ábrázolás összes mátrixai meghatározhatók. Az (5.21), (5.16-17), (5.18), (5.22) képletek alapján közvetlenül adódik:

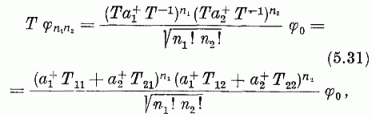
és a binomiális képletet alkalmazva nyerjük az (5.26) eredményt, ahol

*

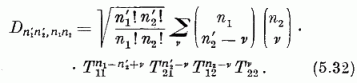
A síkbeli izotróp harmonikus oszcillátor Hamilton-operátorának SU(2) invarianciája kapcsán fent kifejtett formalizmus, ha a szereplő szimbólumoknak alkalmas új jelentést tulajdonítunk, az impulzusmomentum kvantummechanikájának tömör megfogalmazását szolgáltatja. Ezt Schwinger ismerte fel.

Mint (5.20) mutatja, I (ha egységnek ħ-t választjuk) megoldása az impulzusmomentumoperátor felcserélési összefüggéseinek. Az (5.15) (5.13), (5.24), valamint az (5.30) képletekből látható: (5.21) sajátállapota I²-nek a j(j+ 1), I₃-nak az m sajátérték mellett, ahol a

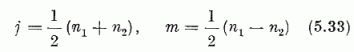
számok mindketten 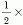egész alakúak. Vezessük be (5.21) helyett a ψ_jm ≡ φ_n1n2 jelölést, ahol j, m és n1, n2 kapcsolatát (5.33) adja meg.

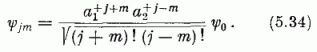
Ekkor (5.30) alapján írható:

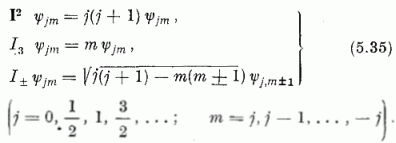
Az impulzusmomentum-operátorok hatását (mátrixelemeit) meghatározó képletek állnak előttünk. - - Az 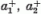operátorokból felépült, (5.34)-ben álló monom fokszáma 2j, így mondhatjuk: egy-egy 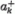a j értékéhez 1/2-del járul hozzá; az m-hez viszont az 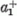operátor + 1/2-del, 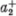pedig - 1/2-del járul. Ennek alapján kézenfekvőnek látszik ψ_jm-et olyan mikrorendszer állapotának tekinteni, melynek j impulzusmomentuma 1/2 spinek eredőjeként áll elő: 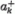az 1/2 spin és + 1/2 spinvetület, 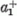az 1/2 spin, - 1/2 spinvetület "keltő" operátora (a₁, a₂ a megfelelő spin- "elnyelő" operátorok). [Ilyen rendszert képeznek pl. az alapállapotú N, P,As,Sb, Bi, (j = 3/2); Mn, Re (j = 5/2); Cr, Mo (j= 3) atomok, az alapállapotú H² Li⁶ (j = 1); Li⁷, Be⁷ (j = 3/2) magok, és a feltevés szerint a Δ s a vele egy családba - az SU(3) dekuplettbe - tartozó gerjesztett nukleonok, melyek 3/2 spinje - vélhető - három kvark 1/2 spinjének eredője.] De mint kitűnik, ψ_jm alkalmazhatósága nem ily korlátozott; az nem csak 1/2 spinekből összetett, hanem tetszőleges j impulzusmomentumií állapot reprezentálására felhasználható. [Ebben az általánosabb esetben (5.34) nem az alkotóelem 1/2 spinek kapcsolódását szemlélteti, hanem azt az alapvető kvantummechanikai törvényt, mely szerint j és m csak 1/2 × egész alakú lehet.] E formalizmus segítségével rövid úton levezethető az impulzusmomentum kvantumelméletének minden ismert eredménye (a forgásmátrixok tulajdonságai; két, három, négy, impulzusmomentum összeadása; a tenzoroperátorok elmélete); sőt, Schwinger még új eredményeket is kapott.

Itt példaként a forgásmátrix kifejezésének leszármaztatására szorítkozunk. - A formalizmust az impulzusmomentum leírására használva az I operátor-vektor mellől az idézőjel természetesen elmarad. Most, ellentétben az oszcillátor esetével, I elforgatása az elsődleges, szemléletes jelentéssel rendelkező transzformáció; az a-ra és a⁺-re alkalmazott SU(2) mátrixok ezen elforgatások kétértékű - ábrázolásának szerepét töltik be itt. Az (5.26) átírásával nyert

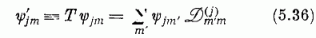
képlet, az impulzusmomentum-sajátfüggvények forgástranszformációját határozza meg. Itt bevezettük az

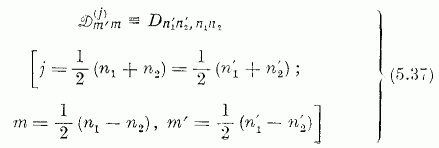
új jelölést. A gyakorlatban az elforgatásokat a forgásvektor helyett inkább a hagyományos Euler-szögekkel jellemzik. Hajtsuk végre először a γ (0,0,γ), majd a β (0,β,0), végül az α (0,0,α) forgásvektorú elforgatást. Azt az elforgatást, mely egymaga helyettesíti e hármat jellemezzük az αβγ Euler-szögekkel. E három elforgatásnak megfelelő mátrixok (1.22-23), szerint

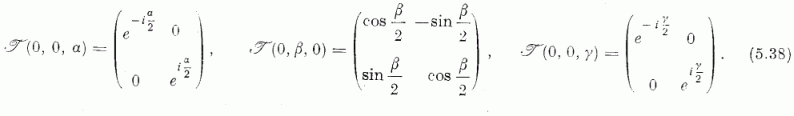
Az αβγ Euler-szögű elforgatáshoz a

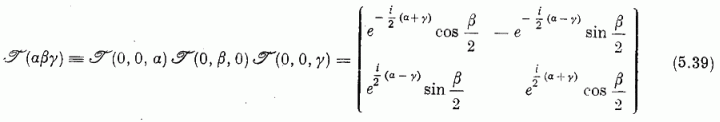
mátrix rendelhető. Ennek T_ij elemeit (5.32)-be helyettesítve és (5.37)-et tekintetbe véve nyerjük azαβγ Euler-szögeknek megfelelő forgásmátrix kifejezését:

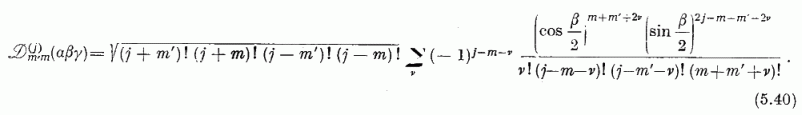
Ez a képlet sűrűn alkalmazásra kerül a sugárzások, a reakciók szögkorrelációjának elméletében.

*

A fentiekben az SU(2) csoporttal különösen sokoldalú szerepben találkoztunk. A síkbeli izotróp harmonikus oszcillátor mozgásegyenleteinek adott megoldásából az SU(2) mátrixai segítségével - mind a klasszikus mind a kvantumelméletben új, az energia ugyanazon értékéhez tartozó megoldás nyerhető; a Hamilton- függvényeknek, ill. operátornak az SU(2) szimmetriacsoportja. A generátorok mozgásállandókat szolgáltatnak. A kvantummechanikában ezen felül egy-egy energiaszinthez az SU(2) csoport meghatározott ábrázolása tartozik. Megjegyzendő, hogy ezek mind irreducibilis ábrázolások: bármiképp válasszuk is az energiasajátállapotok teljes rendszerét, az nem érthető el, hogy egy ilyen ábrázolás minden mátrixa egyöntetűen a ("kvázidiagonális") alakot öltse. Az irreducibililtást mutatja, hogy valamely φ_n1n2 energiasajátállapotból az I± generátorok ismételt alkalmazásával az adott szinthez tartozó minden φ_n1n2 állapot megkapható [lásd (5.30)]. Megemlítjük, hogy egy-egy irreducibilis ábrázoláshoz tartozó energiasajátállapotokat összefoglalóan nevezik multiplettnek; ennek multiplicitása az irr. ábrázolás dimenziója. - Megjegyzendő továbbá, hogy az SU(2) csoportnak nincs olyan irreducibilis ábrázolása, amely az itt találtak közül valamelyikkel ne volna ekvivalens; "ekvivalencia erejéig" az SU(2) csoport összes irreducibilis ábrázolását megkaptuk. (Az ekvivalens ábrázolások az energiasajátállapotok teljes rendszerének más választása mellett állnak elő.) Mindez Lie tételére hivatkozva igazolható, tekintetbe véve, hogy az (5.20) felcserélési összefüggéseknek nincs oly an megoldásuk, amelyből nyerhető ábrázolás ne volna az (5.30) [vagy (5.35)] megoldásokból kapott ábrázolások valamelyikével ekvivalens. - Az SU(2) csoport és a térbeli forgáscsoport között fennálló homomorfia - melyet visszatükröz a generátorok felcserélési törvényeinek azonos alakja is [vö. (1.43-44)] lehetőséget kínál arra is, hogy a síkbeli izotróp harmonikus oszcillátor Hamilton-operátorának SU(2) invarianciájával összefüggésben kifejtett formalizmust felhasználjuk az impulzusmomentum kvantummechanikája tömör megfogalmazására, eredményeinek rövid leszármaztatására. Az SU(2) csoport előbb talált irreducibilis ábrázolásai most a forgáscsoport (egy- vagy kétértékű) irr. ábrázolásainak szerepét töltik be.

Mind a síkbeli izotróp harmonikus oszcillátor Hamilton-operátorának, mind az impulzusmomentum- operátor négyzetének sajátértékfeladata rávilágít a mozgásállandók, az energia operátorának szimmetriacsoportja és az energiaszintek elfajulása, valamint a csoportábrázolások elmélete között a kvantummechanikában fennálló benső kapcsolatra.

(Folytatása következik)