Fizikai Szemle honlap |
Tartalomjegyzék |
Györgyi Géza
Központi Fizikai Kutató Intézet
Induljunk ki a térbeli izotróp harmonikus oszcillátor Hamilton-operátorának
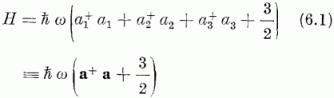
alakjából. Az ak, 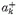 operátorokra az
operátorokra az
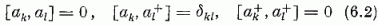
felcserélési összefüggések érvényesek. Az
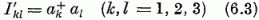
mozgásállandó operátorokra (6.2)-ből az
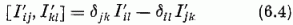
csererelációkat nyerjük.
Legyen  tetszőleges 3 × 3-as unitér
mátrix:
tetszőleges 3 × 3-as unitér
mátrix:  +
+ 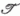 = 1; ezek halmaza az U (3) unitér csoport. Alkalmazzuk
= 1; ezek halmaza az U (3) unitér csoport. Alkalmazzuk 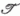 - t
az a(a1, a2, a3) operátor-vektorra
- t
az a(a1, a2, a3) operátor-vektorra

A 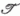 mátrix unitér voltából következik:
a′ +a′ = a+ a; így ezen transzformációval szemben a (6.1)
Hamilton-operátor invariáns.
mátrix unitér voltából következik:
a′ +a′ = a+ a; így ezen transzformációval szemben a (6.1)
Hamilton-operátor invariáns.
A 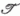 mátrix determinánsának abszolútértéke
egy [vö. (1.15)]. Így
mátrix determinánsának abszolútértéke
egy [vö. (1.15)]. Így 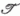 előállítható mint egy
exp iφ tényező s egy unimoduláris mátrix szorzata. Az exp iφ faktor az
időtengely kezdőpontjának eltolását eredményezi. Ha ezen eltolásra érdeklődésünk nem terjed ki,
úgy az U(3) csoportról szorítkozhatunk az SU(3) unimoduláris (vagy speciális) unitér csoportra,
megkövetelve, hogy
előállítható mint egy
exp iφ tényező s egy unimoduláris mátrix szorzata. Az exp iφ faktor az
időtengely kezdőpontjának eltolását eredményezi. Ha ezen eltolásra érdeklődésünk nem terjed ki,
úgy az U(3) csoportról szorítkozhatunk az SU(3) unimoduláris (vagy speciális) unitér csoportra,
megkövetelve, hogy 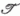 unimoduláris legyen.
unimoduláris legyen.
Megmutatjuk, hogy (6.5) kanonikus (hasonlósági) transzformáció. Jegyezzük meg először, hogy
tetszőleges 3 × 3-as 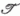 unitér mátrix felirható a
unitér mátrix felirható a

alakban, ahol γ alkalmas 3 × 3-as hermitikus mátrix
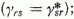 az exponenciális mátrix-függvényt
hatványsora értelmezi. Legyen
az exponenciális mátrix-függvényt
hatványsora értelmezi. Legyen 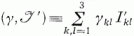 és
képezzük a
és
képezzük a

operátort. Írható

(6.7-8) és (6.5-6) azonossága az exponenciális függvény hatványsorát felhasználva, (6.2-3)
segítségével igazolható. Az unimoduláris 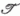 mátrixokra
mátrixokra 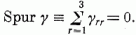 . Ez a feltétel a γ
hermitikus mátrixot meghatározó független paraméterek számát lecsökkenti kilencről nyolcra.
Fölösleges tehát (6.7)-ben a 9 lineárisan független I′ kl operátor;
8 független operátor elég. Legyen
. Ez a feltétel a γ
hermitikus mátrixot meghatározó független paraméterek számát lecsökkenti kilencről nyolcra.
Fölösleges tehát (6.7)-ben a 9 lineárisan független I′ kl operátor;
8 független operátor elég. Legyen
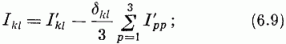
a Spur γ = 0 feltételt felhasználva kapjuk:
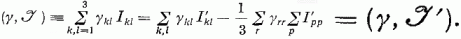
Most tehát (6.7) helyett írható:

Az Ikl operátorok száma ugyan szintén 9, az
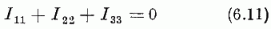
azonosság folytán azonban közülük csak 8 független. Az Ikl-ek csererelációi ugyancsak a (6.4) alakúak:
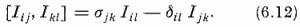
Mint (6.5-8) mutatja, az U(3) csoportot képező kanonikus transzformációkat a 9 független I′&kl generálja, az SU(3) kanonikus transzformációk generátorai pedig (6.10) szerint az Ikl-ek, melyek között 8 független található.
Szokás az SU(3) generátorokat másként is jelölni. Legyen Hk = Ikk és Er = Ikl (k ≠ l); az r vektorális index kapcsolatát a k, l indexpárral nyomban közöljük. A Hk operátorokat egy H (H1, H2, H3) "vektorrá" foglaljuk össze; (6.11) szerint
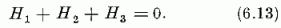
A (6.12) csererelációk ekkor így írhatók:
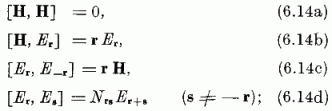
itt az Er ≡ Ikl generátornak megfelelő r "vektor":

ahol
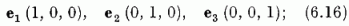
Nrs zérus, +1 vagy -1 aszerint, hogy az r-et és . s-et (6.15) szerint meghatározó k, l és i, j indexpárokra a k ≠ j, l ≠ i, a k ≠ j, l = i s a k = j, l ≠ i relációk közül melyik teljesül. Az r vektorok neve: gyökök [(6.14b) ugyanis sajátértékegyenletként fogható fel, melyben r a sajátérték; r egy-egy komponense a megfelelő szekuláris egyenlet gyöke]. A csererelációk (6.14) alakja a standard vagy kanonikus alak.
*
A térbeli izotróp harmonikus oszcillátor energiasajátállapotainak teljes ortonormált rendszere felírható a
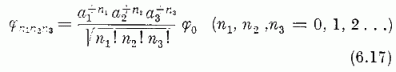
alakban; itt φ0 ≡ φ000 az alapállapot, amelyre ak φ0 = 0 (k = 1. 2. 3). A (6.2) felcserélési összefüggések segítségével nyerhetők az
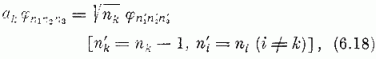
közvetlenül (6.17) alapján pedig az
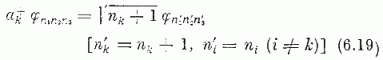
relációk. A (6.1); (6.18-19) képletekből következik:
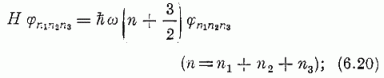
itt ni (i = 1, 2, 3) az oszcillátor i indexű szabadsági fokához tartozó ħ ω kvantumok száma.
Hasonlóan a síkbeli izotróp harmonikus oszcillátor esetéhez, rámutathatnánk arra, hogy a Hamilton-operátornak az SU(3) kanonikus transzformációkkal szemben mutatott invarianciájából következik: valamely energiasajátállapotra a (6.10)-zel adott T operátort alkalmazva, azonos energiasajátértékhez tartozó sajátállapotot nyerünk. Vázolhatnánk most is, mily mértékű az analógia H invarianciájának a klasszikus és a kvantummechanikában adódó következményei között. Rámutathatnánk újból a kvantummechanikában jelentkező merőben új vonásra, ti. arra, hogy ott egy-egy energiaszinthez H invarianciacsoportjának meghatározott ábrázolása tartozik. Nem volna nehéz végül meghatározni - analógiában az SU(2) esetével [vö. (5.32), ill. (5.39)] - az SU(3) csoport azon ábrázolásainak mátrixait sem, amelyek a térbeli izotróp harmonikus oszcillátor energiaszintjeihez tartoznak. E kérdések tárgyalását mellőzzük azonban, s az SU(3) generátorok hatásának megadására szorítkozunk.
A (6.9), (6.3), (6.18-19) képletek alapján írhatjuk:
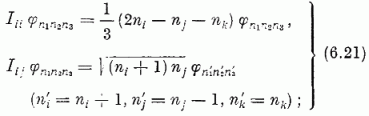
itt i, j, k az 1, 2, 3 számhármast jelöli tetszőleges sorrendben. "Szemléletesebb'' képleteket nyerhetünk a generátorok (6.14)-ben használt H, Er jelölését alkalmazva. A Hi =Iii generátoroknak, mint (6.21) mutatja, φn1n2n3 sajátfüggvénye. A megfelelő sajátértékeket mi-vel jelöljük. Foglaljuk össze ezeket egy m (m1, m2, m3) "vektorrá": m-re a súly elnevezés használatos. A φn1n2n3-hoz tartozó súlyvektor komponensei:
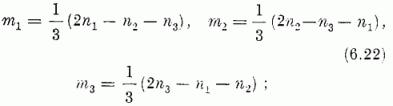
ezek nem függetlenek, közöttük fennáll:
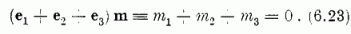
Így ha m-et a sajátállapotok indexelésére kívánjuk használni, további jellemzőre van szükség.
Mondjuk azt - önkényesen -, hogy az m súly az m′ súlynál nagyobb, ha az m-m′ vektor első el nem tűnő komponense pozitív. A legnagyobb súlyt adott n1, + n2 + n3 mellett jelölje j. Ennek komponenseire (6.22) alapján kapjuk:
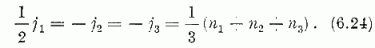
A sajátállapotok jellemzésére j és m (egy, ill. két független komponens) együtt elegendő; ennek alapján a Ψjm ≡ φn1,n2,n3 jelölést is fogjuk alkalmazni.
Legyen
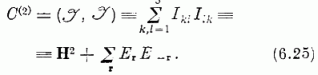
Ez az ún. Casimir-operátor; C(2) valamennyi SU(3) generátorral kommutál.
Az Er, H generátorok és a C(2) Casimir-operátor hatása a Ψjm ≡ φn1,n2,n3 sajátállapotokra eként adható meg:
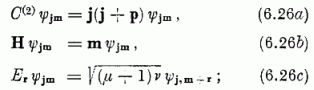
itt p a k < l tulajdonságú, ún. pozitív r = ek, - el, gyökök összege; a µ, v egész számokat a következő feltétel rögzíti: m - µr súly, de m - (µ + 1)r nem az, és m + vr súly, de m + (v + 1)r nem az. A (6.26 b-c) képletek ugyanazt mondják, mint (6.21), más jelölésben; (6.26a) igazolása (6.26b-c), (6.14c) felhasználásával, a Casimir-operátor és a generátorok felcserélhetőségét figyelembe véve történhet. Az analógia (6.26) és az SU(2) generátorokra nyert (5.35) képletek között nyilvánvaló.
A (6.21) vagy (6.26) képletekről az SU(3) csoport említett, a térbeli izotróp harmonikus oszcillátor egyes energiaszintjeihez tartozó ábrázolásainak infinitezimális mátrixai leolvashatók. Ez utóbbiak Lie szerint meghatározzák az ábrázolásokat. Kiemeljük, hogy ezek mind irreducibilis ábrázolások; valamely Ψjm állapotból alkalmas Er generátorok kellő számú alkalmazásával az adott szinthez tartozó bármely Ψjm′ megkapható.
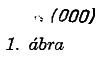 |
 |
 |
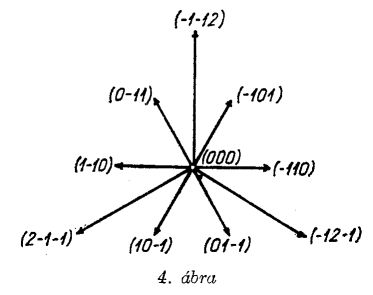 |
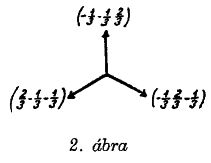
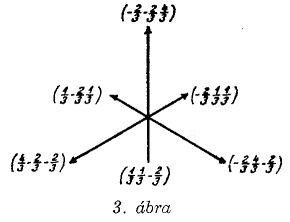
Egy-egy irreducibilis ábrázoláshoz - ha tetszik: szinthez - tartozó m súlyokat [melyek (6.23) szerint
egy síkban fekszenek] felrajzolva adódnak a súlyábrák. Példaként az
n1 + n2 + n3 = 0, 1, 2, 3
esetekre közöljük a súlydiagrammokat (1-4. ábra;
a súlyvektorok végpontjához odaírtuk az m1, m2, m3
komponenseket; a nullvektort kis kör jelzi). A súlyábrák teszik a (6.26) képleteket igazán
szemléletessé. A H operátor-"vektornak" mindegyik Ψjm
sajátállapota; a sajátérték a súlyábra megfelelő vektora. Az Er operátor
j-t szintén változatlanul hagyja, m-et azonban m + r-re
változtatja, vagyis: az r gyökkel megadott irányú és nagyságú "lépést tesz" a súlyábrán
(és még 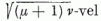 -vel szoroz, minek folytán
ha m + r nem súly, zérust kapunk). Ily módon az Er-ek
segítségével "bebarangolhatjuk" a súlyábrát (ez mutatja az irreducibilitást). A legnagyobb súly
- megfelelően önkényes megállapodásunknak - a szabályos háromszög alakú súlyábra alsó bal
szögpontjába mutató vektor. Ez egyértelműen jellemzi a súlyábrát és vele együtt az SU(3)
megfelelő irreducibilis ábrázolását, továbbá (6.26a) szerint a C(2)
Casimir-operátor sajátértékét. Egy-egy súlyábrához (adott j-vel jellemzett irreducibilis
ábrázoláshoz) tartozó Ψjm állapotok sorozatára a multiplett
elnevezés használatos.
-vel szoroz, minek folytán
ha m + r nem súly, zérust kapunk). Ily módon az Er-ek
segítségével "bebarangolhatjuk" a súlyábrát (ez mutatja az irreducibilitást). A legnagyobb súly
- megfelelően önkényes megállapodásunknak - a szabályos háromszög alakú súlyábra alsó bal
szögpontjába mutató vektor. Ez egyértelműen jellemzi a súlyábrát és vele együtt az SU(3)
megfelelő irreducibilis ábrázolását, továbbá (6.26a) szerint a C(2)
Casimir-operátor sajátértékét. Egy-egy súlyábrához (adott j-vel jellemzett irreducibilis
ábrázoláshoz) tartozó Ψjm állapotok sorozatára a multiplett
elnevezés használatos.
Adott külső mágneses tér pl. egy atomi elektron j impulzusmomentumú energiaszintjét tudvalevőleg a mágneses kvantumszám m = j, j - 1, … ,-j értékeivel jellemzett (a1)szintekre hasítja fel. Az előálló Zeeman-multiplett egy-egy ilyen alszintjének (komponensének) egy-egy Ψjm felel meg: másrészről e Ψjm -ekhez (lásd 5. szakasz) a forgás- ill. SU(2) csoport egy-egy irreducibilis ábrázolása tartozik. Ezen és több más példa (finom- és hiperfinomszerkezet-multiplettek, töltésmultiplettek, nagyobb csoportokkal kapcsolatos mag- és részecske- "szuper"-multiplettek) alapján az empirikus eredetű multiplett szó a csoportelmélet irreducibilis ábrázolás terminuszával a fizikus számára csaknem szinonímává vált.
A multiplettet képező Ψjm-ek száma - az irr. ábr. dimenziója (jele d) - a multiplicitás, melyet a j legnagyobb súllyal a Weyl-féle dimenzióképleteként fejez ki:
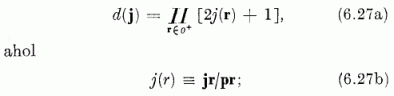
itt a produktumot a pozitív gyökök σ+ rendszerére kell kiterjesztenünk, p pedig - mint fent - a pozitív gyökök összegét jelöli. A (6.27) képletet verifikálhatjuk pl. az 1-4. ábrák multiplettjeire; rendre a d = 1, 3, 6, 10 multiplicitásokat nyerjük.
*
Megemlítjük az SU(3) generátorok néhány szokásos, a fent alapul vett H, Er választástól eltérő definícióját. Legyen
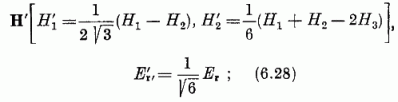
ekkor a H′ (H′1, H′2)
operátor-vektort, a gyököket és a súlyokat két független komponens jellemzi, a gyökökre
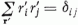 teljesül. - Egy másik használatos definíció,
melynek nyilvánvalóan (5.14) a modellje:
teljesül. - Egy másik használatos definíció,
melynek nyilvánvalóan (5.14) a modellje: 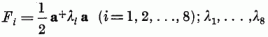 a Pauli-mátrixokkal analóg, 3 × 3-as hermitikus mátrixok, melyeket
Gell-Mann vezetett be (ezeket helykímélés céljából nem írjuk fel). - Elliott választása
helyet ad a generátorok között az
a Pauli-mátrixokkal analóg, 3 × 3-as hermitikus mátrixok, melyeket
Gell-Mann vezetett be (ezeket helykímélés céljából nem írjuk fel). - Elliott választása
helyet ad a generátorok között az 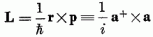 a
pályamomentum
a
pályamomentum
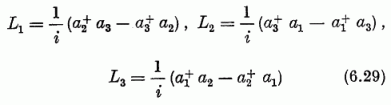
komponenseinek; ezekhez járul az öt
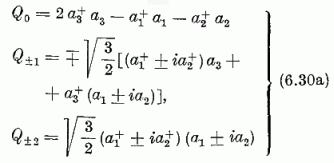
generátor, melyeket tömörebben így is felírhatunk:
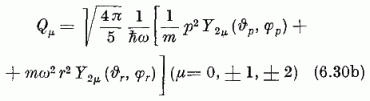
υr, φr a helyvektor, υp,φp pedig az impulzus vektorának polárszögei).
A térbeli izotróp harmonikus oszcillátor gyakran szolgál a problémák tárgyalásának kiindulópontjául
az elméleti magfizikában. Nulladik közelítésben megfelelő lehet a feltevés, mely szerint az
atommag nukleonjai a magcentrumtól mért távolsággal arányos visszatérítő erő hatása alatt
végzik mozgásukat. Az A tömegszámú magot jellemző H Hamilton-operátor
ebben a közelítésben az A számú nukleon (6.1) mintára felírt H(1), …,
H(A) Hamilton-operátorainak összege. Ez a H Hamilton-operátor -
hasonlóan az egyes H(i)-khez - invariáns az SU(3) csoporttal szemben; így
H sajátállapotai is SU(3) multiplettekbe osztályozhatók: - A fenti "független-részecske
oszcillátor-modell" persze túlzott egyszerűsítést jelent. A valóság jobb megközelítése a nukleonok
között ható kéttest-erők  potenciáljának
bevezetésével érhető el. A V(ij) potenciálfüggvény alakjára s a fellépő paraméterek
értékére tett "észszerű" feltevések mellett elvégzett numerikus számítások ténylegesen jó
eredményeket adtak az 1p nukleonhéj feltöltésével kiépülő magok (4 < A ≤ 16)
spektrumára, valamint az 1d-2s héj kezdetén (A = 19-ig); ennél
nehezebb magokra az ilyen számítások nehézségei legyőzhetetlenekké válnak.
potenciáljának
bevezetésével érhető el. A V(ij) potenciálfüggvény alakjára s a fellépő paraméterek
értékére tett "észszerű" feltevések mellett elvégzett numerikus számítások ténylegesen jó
eredményeket adtak az 1p nukleonhéj feltöltésével kiépülő magok (4 < A ≤ 16)
spektrumára, valamint az 1d-2s héj kezdetén (A = 19-ig); ennél
nehezebb magokra az ilyen számítások nehézségei legyőzhetetlenekké válnak.
Figyelmet érdemel itt egyes magok esetében a forgási állapotok fellépte. Ezek forgási sávokba sorolhatók; egy-egy sávon belül a gerjesztési energia (legtöbbször) a magspin-operátor négyzetének I (I + 1) sajátértékével arányos. Forgási sávokat korábban nagy számban észleltek nehéz magok spektrumában. Az egészen könnyű magok között régóta ismert példa a Be8 mag sávja (5. ábra). Az ötvenes évek derekától kezdődően további könnyű magokban azonosítottak forgási sávokat (pl. F19, Ne20; Mg24 stb.; lásd 6. ábra). A forgási állapotok egyrészről leírhatók a Bohr-Mottelson-féle fenomenológikus modellel, mely feltételezi a deformált "magtörzs" létét s ehhez esetleg egy-két külső nukleont csatol, másrészről felmerülhet természetesen az igény a mikroszkópikus leírásra, mely a magot mint A számú, kölcsönhatásban álló nukleon rendszerét fogja fel. Különösen természetes a mikroszkópikus leírás igénye a könnyű magok forgási állapotai esetében; hisz' Be8, F19 benne fekszik a magoknak abban a tartományában, ahol az oszcillátor-modell alapján, kétnukeon-erők bevezetésével elvégzett számítások jó eredményeket adtak a spektrumokra, s a többi ilyen mag (Ne20, Mg24 stb.) is e tartomány szomszédságában található. Az F19 mag esetében ténylegesen bebizonyosodott, hogy a kétféle leírás - a fenomenológikus és mikroszkópikus - egymással és a tapasztalattal összhangban álló eredményekre vezet. Várhatóan másutt is fennáll az összhang, az ennél nehezebb magokra azonban az ilyen összehasonlításnak útját állják a mikroszkópikus leírással járó legyőzhetetlen számítási nehézségek (a kétnukleon-kölcsönhatás diagonalizálandó energiamátrixa nagyságrendben 100 × 100-as és annál nagyobb is lehet). Természetes gondolat, hogy az oly egyszerű képet mutató forgási spektrumok mikroszkópikus értelmezéséhez ennél egyszerűbb úton is el kell tudnunk jutni.
A térbeli izotróp harmonikus oszcillátor és az SU(3) csoport kapcsolatát felhasználva Elliott adott meg olyan - egyszerű, nagymértékben idealizált - mikroszkópikus magmodellt, amely forgási sávok felléptére vezet. Az Elliott-modell Hamilton-operátora:
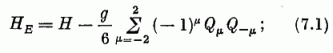
itt H a független részecske oszcillátor-modell Hamilton-oprátora, mely az egyes nukleonok (6.1) alakú Hamilton-operátorainak összege, Qµ pedig az egyes nukleonoknak megfelelő, a (6.30) mintára képezett SU(3) generátorok összegét jelöli:
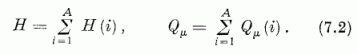
A (7.1) részletes kiírásakor előálló
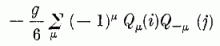
alakú tagok kölcsönhatást eredményeznek az i-edik és a j-edik nukleon között. Ez az ún. kvadrupól-kölcsönhatás nyilvánvalóan mesterkélt, nem tükrözi híven a valóságos nukleon-nukleon erők minden lényeges tulajdonságát, mindazonáltal mutat bizonyos "realisztikus" vonásokat. Így ha pl. az i-edik nukleon mozgását a z-tengely mentén végzi, úgy a j-edik nukleonnak - mint az (6.30), (7.1-2) alapján megállapítható - energetikailag előnyös mozgását ugyancsak a z-tengely mentén kell végeznie. A nukleonok mozgásában a kvadrupól-kölcsönhatástól előidézett korreláció eszerint a mag (kvadrupól-jellegű, ellipszoidális) deformációját eredményezi, amit éppen a forgási spektrummal rendelkező magoknál meg is lehet figyelni.
A független-részecske oszcillátor-modell H Hamilton-operátora - mint már említettük - természetesen SU(3) invariáns; HE azonban nem az, a kvadrupól-kölcsönhatás ugyanis "sérti" az invarianciát. Az SU(3) csoport mégis segítségünkre van: HE ugyanis kifejezhető SU(3) generátorokkal és sajátértékfeladata ezen az úton könnyűszerrel megoldható.
Az SU(3) transzformációk, melyek minden egyes nukleon a (i) operátor-vektorát (i= 1, 2,…, A) egyöntetűen (6.5), (6.8) szerint transzformálják, generálhatók pl. az egyes nukleonokra (6.9), (6.3) alapján felírt Ikl(i)-ket összegezve adódó
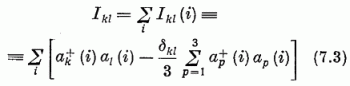
generátorokkal; de ugyancsak használhatjuk generátorként az
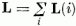 eredő pályamomentum 3 komponensét s a (7.2)-vel
megadott 5 Qµ operátort. A Casimir-operátor [vö. (6.25)] a
generátorok mindkét fajtájával egyszerű alakban kifejezhető:
eredő pályamomentum 3 komponensét s a (7.2)-vel
megadott 5 Qµ operátort. A Casimir-operátor [vö. (6.25)] a
generátorok mindkét fajtájával egyszerű alakban kifejezhető:
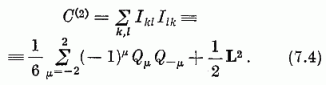
Mint látjuk, a kvadrupól-kölcsönhatás kifejezhető a C(2), L2 operátorokkal; írjuk (7.1) helyett:
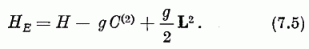
A független-részecske oszcillátor-modell H Hamilton-operátornak E0
sajátértékeit az egyes nukleonok 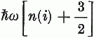 oszcillátor-energiáinak összege adja:
oszcillátor-energiáinak összege adja: 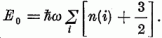 .
Minthogy a H operátor SU(3) invariáns, sajátállapotait - a korábban mondottak szerint -
oly módon választhatjuk, hogy azok SU(3) multipletteket alkossanak. Egy-egy ilyen multiplett
komponensei a C(2) Casimir-operátornak sajátállapotai; ha a
multiplettet egyértelműen jellemző legnagyobb súlyt J jelöli, úgy C(2)
sajátértéke J(J + p) [vö. (6.26); p az SU(3) pozitív
gyökeinek összege]. Ha végül képezzük az SU(3) multiplett-komponensek azon lineáris
kombinációit, amelyek L2-nek is sajátállapotai, a (7.5) Hamilton-operátor
sajátértékfeladatának megoldását nyerjük.
.
Minthogy a H operátor SU(3) invariáns, sajátállapotait - a korábban mondottak szerint -
oly módon választhatjuk, hogy azok SU(3) multipletteket alkossanak. Egy-egy ilyen multiplett
komponensei a C(2) Casimir-operátornak sajátállapotai; ha a
multiplettet egyértelműen jellemző legnagyobb súlyt J jelöli, úgy C(2)
sajátértéke J(J + p) [vö. (6.26); p az SU(3) pozitív
gyökeinek összege]. Ha végül képezzük az SU(3) multiplett-komponensek azon lineáris
kombinációit, amelyek L2-nek is sajátállapotai, a (7.5) Hamilton-operátor
sajátértékfeladatának megoldását nyerjük.
Megjegyzendő, hogy a J legnagyobb súly helyett, melynek komponensei nem mind
függetlenek, az SU(3) multiplettek jellemzésére J komponenseinek
λ = J1 - J2, µ = J2 - J3
kombinációi is használatosak; C(2) sajátértéke ezekkel a
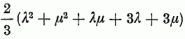 alakban fejezhető ki.
alakban fejezhető ki.
Az Elliott-modell HE Hamilton-operátorának E sajátértékét a H operátor E0 sajátértékének, a Casimir-operátor sajátértékének, valamint az L2 operátor L (L + 1) sajátértékének kombinációja alakjában nyerjük:
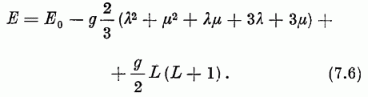
Adott E0 és λ, µ mellett az E energiasajátérték az L impulzusmomentum-kvantumszámtól a forgás spektrumokra jellemző függést mutatja.
*
Milyen SU(3) multiplettek, s ezeken belül milyen forgási sávok lépnek fel valamely adott magban? Az általános válasz hosszadalmas ábrázoláselméleti megfontolásokat igényel; itt csupán néhány egyszerű példát veszünk szemügyre.
Az első, legegyszerűbb példa: két részecske az n = 1 oszcillátor-kvantumszámú szinten. A kétrészecske-rendszer ilyen állapotai a
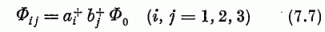
alakban írhatók fel; Φ0 a rendszer alapállapota (mindkét részecske az
n = 0 szinten), 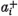 az egyik,
az egyik,
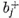 a másik részecskéhez tartozik.
Képezzük a (7.7) állapotok
a másik részecskéhez tartozik.
Képezzük a (7.7) állapotok
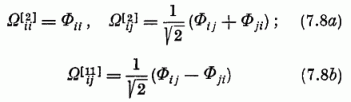
kombinációit; a hat szimmetrikus Ω[2] s a három antiszimmetrikus Ω[11] ugyanúgy teljes ortonormált rendszert képez, mint a kilenc Φij állapot.
Az SU(3) generátorok a kétrészecske-rendszer esetében (7.3) szerint:
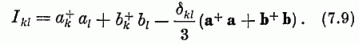
Most is célszerű a Hk = Ikk, Er = Ikl (k ≠ l; r = ek - ei) jelölés használata. A H (H1, H2, H3) operátor-vektor alkalmazásával megállapíthatjuk, hogy a (7.8) állapotok valamennyien meghatározott M súlyhoz tartoznak. Az Er operátort valamely M súlyhoz tartozó állapotra alkalmazva az M + r súlyhoz tartozó állapotot nyerünk, egy faktorral szorozva (ill. zérust, ha M + r nem súly) ; a [2], ill. [11] felső index eközben érintetlen marad. A (7.8a) állapotok esetében a 3. ábrán közölt hat súlyvektor adódik; a (7.8b) alatt felírt három állapothoz tartozó súlyokat a 7. ábra mutatja.
Ha az állapotok indexelésére a súlyokat vezetjük be, a generátorok hatását a (6.26) mintára áttekinthető képletekkel fejezhetjük ki. A (7.8) állapotok alsó indexpárjának szerepét M veszi át, a (7.8a) és (7.8b) állapotok megkülönböztetésére pedig a szögletes zárójelbe foglalt indexcsoport helyett a J legnagyobb súlyt alkalmazzuk. Ha az i, j alsó indexpárban az 1, 2, 3 számok rendre N1-szer, N2-ször, N3-szor fordulnak elő, úgy a megfelelő M súly komponenesei:
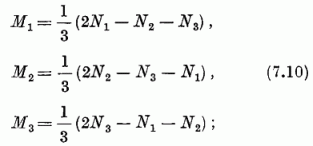
Nk természetesen a k indexű, a és b típusú oszcillátor-kvantumok számának összegét jelenti [vö. (6.22)]. Ily módon bevezetve a (7.8) állapotokra a ΨJM jelölést, a
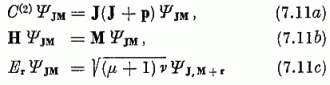
képleteket nyerjük; itt µ v hasonló jelentésű, mint (6.26)-ban.
Helyezzünk most egy részecskét az n = 2, egyet az n = 1 oszcillátor-szintre. Ilyen állapotok egy teljes ortonormált rendszere:
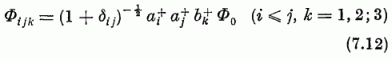
(18 állapot). Képezzük ezekből a jk indexpárban antiszimmetrikus kilenc
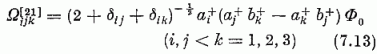
kombinációt. Ezek valamennyien normáltak, az i = j vagy i = k állapotok egymásra s a többi állapotra is ortogonálisak, az ijk = 123, 213, 312 állapotok azonban egymásra nem ortogonálisak és nem is függetlenek; független és egymásra is ortogonális állapotok azonban pl.
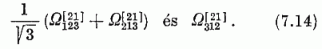
A (7.13) állapotok közül azok, amelyekre i = j vagy i = k, továbbá a (7.14) állapotok együttvéve (számuk összesen 8) ortonormált sorozatot képeznek. Meg lehet győződni arról, hogy itt egy SU(3) multiplettel állunk szemben; a súlydiagramm a 8. ábrán látható. Figyelmet érdemel, hogy a zérustól különböző súlyok megegyeznek a (6.15) gyökvektorokkal. Ezt a multiplettet az SU(3) reguláris multiplettjének nevezzük; a megfelelő irr. ábrázolás neve reguláris ábrázolás. Az SU(3) generátorok hatása most is áttekinthetőbbé tehető az állapotok indexeként az M súlyokat alkalmazva; némi bonyodalmat okoz azonban az az új vonás, hogy van olyan súly (M = 0), amelyhez két lineárisan független állapot tartozik.
Megemlítjük, hogy a most talált nyolckomponensű multiplett (oktett) mellett a (7.12) állapotokból képezhető még egy tízkomponensű SU(3) multiplett (dekuplett; a súlyokat lásd a 4. ábrán) is; ezen oktett és dekuplett együttesen helyettesíteni képes a 18 állapotból álló (7.12) ortonormált rendszert.
*
Röviden utalunk az egyes SU(3) multiplettek jellegzetes szimmetriatulajdonságaira. Így (7.8a) alatt ij-ben szimmetrikus, (7.8b) alatt antiszimmetrikus-állapotokat látunk; e szimmetriatulajdonságokat szokás a
ún. Young-ábrákkal szemléltetni. Az egy sorban álló négyzetek szimmetriára, az egy oszlopban állók antiszimmetriára utalnak. A (7.13) állapotok a
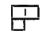
Young-ábrával szemléltethetők; az egy oszlopban
álló két négyzet a jk indexpárban fennálló antiszimmetriára utal. A Young-ábra
közlése helyett sokszor az egy-egy sorban álló négyzetek számát adják meg, szögletes
zárójelbe zárva. Így 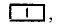 ,
,
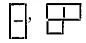 helyett rendre [2], [11], [21] írható;
ezeket a szimbólumokat alkalmaztuk (7.8), (7.13-14) alatt felső index gyanánt.
helyett rendre [2], [11], [21] írható;
ezeket a szimbólumokat alkalmaztuk (7.8), (7.13-14) alatt felső index gyanánt.
Minthogy a szereplő indexek háromértékűek, antiszimmetria legfeljebb három indexben állhat fenn. Az SU(3) multiplettek Young-ábrái így legfeljebb háromsorosak lehetnek; a szögletes zárójeles szimbólum az általános esetben tehát három számból áll: [f1f2f3] (a zérussal egyenlő fi-ket nem szoktuk kiírni).
A Young-ábrák e futólagos jellemzésének kiegészítéseképpen közöljükaz [f1f2f3] szimbólum kapcsolatát az SU(3) multiplettek másfajta jellemzőivel. A legnagyobb súly komponensei a
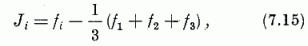
a (7.6) alatt használt λ, µ pedig a
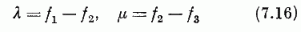
kapcsolatban állnak az fi-kel. Az f1 + f2 + f3 összeget J vagy λ, µ nem határozza meg; az a háromértékű SU(3) indexek száma.
*
A kérdés, hogy adott SU(3) multiplettben milyen forgási sávok, az L impulzusmomentum-kvantumszám mely értékei lépnek fel, még válaszra vár. Újra csak példákra szorítkozunk. A (7.7-8) példában L a két részecske l = 1 momentumainak eredőjeként adódik: L = 0, 1, 2. A Wigner-féle impulzusmomentum-összeadási együtthatók szimmetriatulajdonságai azt mutatják, hogy ezek közül L = 0, 2 a [2] multipletthez, L = 1 pedig [11]-hez tartozik. A (7.13) példa [21] oktettje esetében az L = 1, 2, a (7.12)-ből képezhető dekulpettben (szimbóluma [3]) pedig az L = 1, 3 értékek lépnek fel.
*
A fenti példák mintája szerint elemezve a Be8 mag n = 1 oszcillátor-szinten helyetfoglaló 4 külső nukleonjának állapotait, megállapíthatjuk először is, hogy a fellépő SU(3) multiplettek [4], [31], [22], és [211]. A megfelelő (λµ) értékpárok (7.16) szerint (40), (21), (02) és (10); ezeket rendre (7.6)-ba helyettesítve azt találjuk, hogy legalacsonyabban a (40) multiplett fekszik, mely a 0, 2, 4 impulzusmomentum-értékeket egyesíti magában. Az 5. ábra mutatja, hogy az elmélet e következtetése a megfigyeléssel összhangban áll.
A Mg24 mag legmélyebben fekvő SU(3) multiplettjére hasonló módon (λµ) = (84) adódik; ez egy 0, 2, 4, …, egy 2, 3, 4, …, valamint egy 4, 5, … forgási sávot foglal magában. A 6. ábrán, mely Mg24 megfigyelt spektrumát 6 MeV-ig mutatja, az előbbi két sáv jól felismerhető; a harmadik valószínűleg igen magasan, 15 MeV táján fekszik. Tanulságos végül egybevetni Mg24 és Ne20 spektrumát. Az utóbbi legmélyebb SU(3) multiplettjére (80) adódik a 0, 2, 4, 6, 8 impulzusmomentum-tartalommal. Ezt a sávot, mely Mg24 alapállapoti sávjával analóg, megfigyelték; míg azonban Mg24 spektrumában fellép egy alacsonyan fekvő 2, 3, 4, … sáv is, Ne20 esetében ilyen nem észlelhető, összhangban a modellel.
Az erős kölcsönhatásokban jelentkező különféle részecskeállapotoknak, barionoknak és mezonoknak, vagy közös nevükön hadronoknak ma már se szeri, se száma. Példaképpen a két legismertebb barion-családot ragadjuk ki (9. és 10. ábra). A 9. ábrán bemutatott nyolctagú barion-család, a barionoktett a nukleonok [a proton (P) és a neutron (N)] mellett a Λ, a három Σ és a két Ξ hiperont foglalja magában. Az utóbbiak viszonylag hosszú (~ 10-10 s) élettartamú barionok, melyeket az ötvenes években fedeztek fel. A 10. ábrán látható családnak jóideig csak kilenc tagja volt ismert. A Δ részecskeállapotokat a pion-nukleon szórás vizsgálata során Fermi fedezte fel (1952), a Σ*, Ξ* állapotokat a hatvanas évek kezdetén ismertük meg. Ezek élettartama igen rövid (~10-23 s) és azok rezonanciaként észlelhetők. A részecskecsaládok egyes tagjaira jellemző Q töltésük; ezen kívül azonban szükséges legalább még egy jellemző. Az Y hipertöltés nemcsak az egyes szinteket különbözteti meg a 9. és a 10. ábrán, de a rá vonatkozó kiválasztási szabályok jellemzik a különféle átalakulások valószínűségét is.
Gell-Mann és Ne'eman felismerése szerint ezen részecskecsaládok
megfeleltethetők bizonyos SU(3)
multipletteknek. Az SU(3) súlydiagrammokon az egy-egy vízszintes egyenes mentén elhelyezkedő
multiplett-komponenseket az m súlyvektor harmadik komponensének ugyanazon értéke
jellemzi; az egy-egy vízszintes egyenesen elhelyezkedő barionokhoz pedig ugyanazon Y
hipertöltés tartozik. A megfeleltetés első lépéseként a súly m3
komponense az Y hipertöltés -1-szeresével azonosítható. A 9. ábra
barion-oktettjét a 8. ábra SU(3) oktettjével egybevetve azt
látjuk, hogy m első komponense az egyes barionok töltését adja meg: Q = m1;
hasonló megállapítást tehetünk a 10. ábra részecske-családját
a 4. ábra súlydiagrammjával összevetve; a T3
kvantumszám az m súlyból pl. az 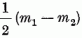 alakban
nyerhető.
alakban
nyerhető.
Az SU(3) csoport szerepének felismerése a részecskefizikában a hadronok csoportelméleti osztályozására irányuló sokéves erőfeszítések gyümölcse. A független SU(3) generátorok száma nyolc lévén, Gell-Mann elméletének a nyolcas út nevet adta, utalva a Buddhától kijelölt "nemes nyolcas út"-ra, mely "a fájdalom megszűnéséhez vezet".
A részecskecsaládok és az SU(3) multiplettek között létesíthető megfeleltetés első pillantásra talán puszta érdekességnek látszik, különösebb fizikai következmények nélkül. Valójában a hadronok ezen osztályozása igen gyümölcsözőnek bizonyult. A 10. ábrán látható családnak - mint említettük - kezdetben csak kilenc tagja volt ismert. Gell-Mann érdeme a felismerés: ha ezekhez egy tizedik, Y = - 2 hipertöltésű, Q = - 1 töltésű részecske csatlakoznék, úgy e családnak a 4. ábra SU(3) multiplettje, a dekuplett volna megfeleltethető. Gell-Mann ezen jóslata ragyogó igazolást nyert: az Ω- részecskét rövidesen sikerült kísérletileg kimutatni (1964).
A nyolcas út másik sikere a Gell-Mann és Okubo által nyert tömegformula. Írjuk
fel a barionok osztályozásában szerepet kapott SU(3) multiplettek, az oktett és a dekuplett
komponenseit. Az oktettkomponenseket (7.13-14) alatt két operátor-hármas:
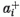 és
és 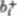 (i = 1, 2, 3) segítségével sikerült megszerkeszteni. Felhasználva ezt az eredményt, a
nyolctagú barion-család és az SU(3) oktett között létesített megfeleltetés részletesen így írható
fel:
(i = 1, 2, 3) segítségével sikerült megszerkeszteni. Felhasználva ezt az eredményt, a
nyolctagú barion-család és az SU(3) oktett között létesített megfeleltetés részletesen így írható
fel:
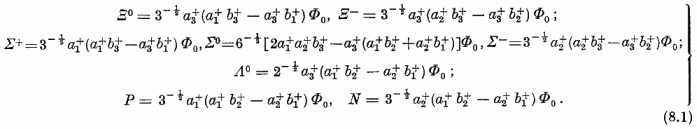
A dekuplett-komponensek megszerkesztéséhez egy 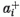 (i = 1, 2, 3) operátor-hármas is elég; dekuplettet képeznek a térbeli izotróp harmonikus
oszcillátor n = 3-hoz tartozó (6.17 ) energiasajátállapotai. A tíztagú barion-család
tagjainak az SU(3) dekuplett komponenseivel való azonosítása részletesen:
(i = 1, 2, 3) operátor-hármas is elég; dekuplettet képeznek a térbeli izotróp harmonikus
oszcillátor n = 3-hoz tartozó (6.17 ) energiasajátállapotai. A tíztagú barion-család
tagjainak az SU(3) dekuplett komponenseivel való azonosítása részletesen:
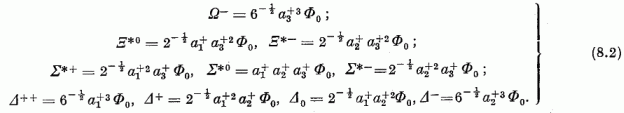
A megfelelő SU ( 3 ) generátorok, mint ( 7. 9 ) alatt is :
Képezzük ezekből a
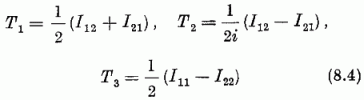
kombinációkat. A T (T1,T2,T3) "vektor" az SU(2) generátorok

felcserélési összefüggéseinek tesz eleget. A T± = T1 ± iT2 operátorok a neutront protonba, ill. a protont neutronba, általában a (8.1-2) képletek egy-egy sorában álló töltésmultiplettek szomszédos komponenseit egymásba transzformálja. A T operátor-vektor az izospin operátora. A T2 operátor T (T +1) sajátértékét meghatározó T izospinkvantumszám segítségével az egyes töltésmultiplettek multiplicitása az ismert 2T + 1 alakban írható fel.
A barionok nyugalmi energiáját képviselő Hamilton-operátor nem SU(3) invariáns, hiszen ha az volna, egy-egy SU(3) multiplett egyenlő nyugalmi energiájú (tömegű) részecskeállapotokat egyesítene magában. Legfeljebb közelítő SU(3) invarianciáról lehet beszélni, arra hivatkozva, hogy a 9. és 10. ábrákon a tömegfelhasadás viszonylag csekély. Feltehetjük, hogy az SU(3) invarianciát megsértő pertubációs operátor - mely a tömegfelhasadást eredményezi, éppúgy mint a mágneses tér a Zeeman-felhasadást - egyszerű szerkezetet mutat. Szem előtt tartva a lineáris Zeeman-effektust, a legegyszerűbb feltevés az, hogy ez a perturbációs operátor H3 - I33-mal arányos. Ekkor azonban az oktettben nem lép fel a Σ - Λ felhasadás. Tartalmazzon ezért a perturbációs operátor egy a generátorokban kvadratikus tagot is, mellyel azonban a (8.4) izospin-operátor legyen felcserélhető. Ennek alapján választásunk:
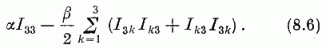
A második tag így is írható: 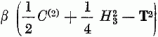 . A (8.6)
operátor sajátértéke adja meg a tömegfelhasadást:
. A (8.6)
operátor sajátértéke adja meg a tömegfelhasadást:
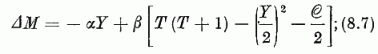
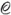 -vel a Casimir-operátor sajátértékét
jelöltük. Ez Gell-Mann és Okubo tömegképlete. Az oktett- és
dekuplett-komponensek tömegére a
-vel a Casimir-operátor sajátértékét
jelöltük. Ez Gell-Mann és Okubo tömegképlete. Az oktett- és
dekuplett-komponensek tömegére a
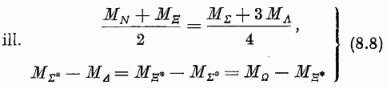
összefüggést kapjuk. Mindkettő igen jól teljesül. - A (8.7) képletet használta fel Gell-Mann arra, hogy megjósolja az Ω- tömegét, továbbá a ΔY = 1 szabálynak megfelelő lassú bomlását.
Látjuk, hogy a Gell-Mann és Ne'eman által megadott osztályozás gyümölcsözően használja fel az SU(3) multipletteket és generátorokat, ugyanakkor azonban az SU(3) csoport és ábrázolásainak mátrixai számára nem juttat semmilyen szerepet. Ez - hasonlóan a másutt látott ilyen esetekhez (pl. izospin) - a töltést, ill. a hipertöltést illető szuperkiválasztási elvvel áll kapcsolatban.
*
Figyelmet érdemel, hogy a "nyolcas út" a hadronok osztályozására kizárólag olyan SU(3)
multipletteket használ, amelyek összesen három 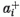 ,
ill.
,
ill. 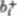 operátor alkalmazásával képezhetők
[lásd (8.1-2)]. Vajon van-e a természetben szerepük más SU(3) multipletteknek is, mindenek előtt
a legegyszerűbb nemtriviális - ún. fundamentális multipletteknek (lásd a 2.,
7. ábrák súlydiagrammjait)? Ezt a kérdést először Gell-Mann
és Zweig vette fel, rámutatva arra, hogy ezen multipletteknek
operátor alkalmazásával képezhetők
[lásd (8.1-2)]. Vajon van-e a természetben szerepük más SU(3) multipletteknek is, mindenek előtt
a legegyszerűbb nemtriviális - ún. fundamentális multipletteknek (lásd a 2.,
7. ábrák súlydiagrammjait)? Ezt a kérdést először Gell-Mann
és Zweig vette fel, rámutatva arra, hogy ezen multipletteknek 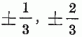 elektromos, barion- és hipertöltésű részecskék felelnének meg. Gell-Mann e feltételezett
részecskéknek a kvark nevet adta.
elektromos, barion- és hipertöltésű részecskék felelnének meg. Gell-Mann e feltételezett
részecskéknek a kvark nevet adta.
Szabad kvarkot mindeddig nem figyeltek meg. Sok esetben igen gyümölcsözőnek bizonyult azonban a feltevés, mely szerint minden hadron kvarkokból épül fel. Eszerint az ismert barionok három kvarkból állanának, a mezonokat pedig kvark-antikvark-pár képezné.
Az 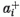 ,
, 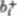 operátorokat fent matematikai segédeszközként használtuk fel, de tekinthetnénk azokat kvark-keltő
operátornak is; a három
operátorokat fent matematikai segédeszközként használtuk fel, de tekinthetnénk azokat kvark-keltő
operátornak is; a három 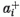 operátor
(i = 1, 2, 3) természetesen a kvark térbeli mozgásáról nem, csak elektromos és
hipertöltéséről ad számot. Az SU(3) multiplettek hadronfizikai jelentőségének alapját talán a
fundamentális kvark-triplett létezése, az
operátor
(i = 1, 2, 3) természetesen a kvark térbeli mozgásáról nem, csak elektromos és
hipertöltéséről ad számot. Az SU(3) multiplettek hadronfizikai jelentőségének alapját talán a
fundamentális kvark-triplett létezése, az 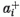 kvark-operátor indexének "trichitomiá"-ja képezi.
kvark-operátor indexének "trichitomiá"-ja képezi.
Megvilágítást igényel a kérdés, eddig azonban elsiklottunk felette: Mit jelent az, hogy míg a (8.2)
dekuplett egyedül az 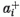 (i = 1, 2, 3)
operátorhármas segítségével is felépíthető, a (8.1) oktett megszerkesztéséhez feltétlenül szükséges
egy további
(i = 1, 2, 3)
operátorhármas segítségével is felépíthető, a (8.1) oktett megszerkesztéséhez feltétlenül szükséges
egy további 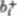 (i = 1, 2 , 3) hármast
bevezetnünk? Ha ezen operátorokat kvark-operátorokként értelmezzük, miben különböznek
egymástól az a- és a b-kvarkok? Mindezek a kérdések a
hadron-szupermultiplettek elméletéhez vezetnek (10. szakasz).
(i = 1, 2 , 3) hármast
bevezetnünk? Ha ezen operátorokat kvark-operátorokként értelmezzük, miben különböznek
egymástól az a- és a b-kvarkok? Mindezek a kérdések a
hadron-szupermultiplettek elméletéhez vezetnek (10. szakasz).
(Folytatása következik)