|
|
(1.1) |
Fizikai Szemle honlap |
Tartalomjegyzék |
Györgyi Géza
KFKI
"Gondolatok a fizika tanításának néhány kérdéséről" című kiváló cikkében 1 Holics László szép és igaz gondolatokat fogalmaz meg a mechanikaoktatásról, a természeti folyamatok kvantitatív megfogalmazásáról, a deduktív módszerről:
"A mechanika tanítja meg (a tanulót) a lehető legegyszerűbb objektumokon megfigyelni a változásokat, jelenségeket, egzakt kvantitatív formába foglalni az egyszerű folyamatokat." Itt tanul meg deduktíve eljutni új, meg nem figyelt igazságokhoz és itt csodálja meg először a természetmagyarázó elvek lenyűgöző teljesítőképességét..." Majd Marx György szavaira hivatkozik: ... az egész fizikaoktatásban lényeges szerepet kell juttatni a dinamikai alaptörvények tanításának . . . velük kell illusztrálnunk a természettörvény fogalmát, szerepét, rajtuk keresztül kell rámutatni a természeti jelenségek gazdag változatossága mögött rejlő egyszerű és mély összefüggésekre."
Még Vermes Miklós írásából szeretnénk idézni; Mikola Sándorról írva említi, 2 hogy az ő számára "a fizika centrális része a Newton-axiómák, a gravitáció, a Kepler-törvények . . . területén feküdt."
Valóban, a Newton-axiómák, a gravitációs törvény és a Kepler-probléma fontosságát a fizika fejlődésében és felépítésében aligha lehet eléggé hangsúlyozni. A Newton-féle dinamikai alaptörvények oktatásának még nyomatékosabbá, elmélyültebbé kell válnia, különös tekintettel a sürgető szükségletre, hogy a relativitáselmélet és a kvantummechanika alapjai is helyet kapjanak a középiskolai oktatásban. A Kepler-probléma pedig prototípusa az egyszerű folyamatnak, melyből deduktíve új igazságokhoz juthatunk, mindenekelőtt Newton gravitációs és dinamikai törvényeihez; de ezeken túl hosszú a sora azoknak a fontos fizikai tényeknek és törvényeknek, amelyeknek felismerése a Kepler-problémához kapcsolódik.
Jogosnak tetszik tehát lehetőségek után kutatni, melyek a Kepler-mozgást s vele összefüggésben Newton dinamikai törvényeit közelebb hozhatják a tanulóhoz s számára élményszerűbbé tehetik. Mindenekelőtt szeretnénk rámutatni: a Kepler-mozgás időbeli lefolyását kvantitatív alakban kifejező (2.5) Kepler-féle időegyenlet a bolygómozgást tárgyaló gimnáziumi fizikakönyv 3 matematikai eszközeinek hatósugarán belül fekszik. Kitűzhető feladatul a Kepler-pálya megrajzolása, a pálya egyes pontjai mellett feltüntetve a megfelelő időpontokat. A pálya jellemző adataiból kiszámítható pl., milyen messze jár most a Halley-üstökös, mennyivel hosszabb a nyarat magában foglaló félév, mint az a félév, amely a telet foglalja magában, nyomonkövethető a műholdak - közöttük a gyakorlatilag fontos, nyújtott pályán keringő "Molnija-I" távközlési holdak - mozgása. Ugyanezen matematikai eszközök birtokában ugyancsak könnyen megszerkeszthető a hodográf görbéje [a sebesség-ábra; lásd a (3.5) vagy a (3.12) képletet]. A folyamatok kvantitatív formába foglalására ezek a feladatok bizonyára elmélyültebben tanítanak, mint a Kepler-törvények szövegének emlékezetben való rögzítése, vagy az egyenlő idők alatt súrolt területek egyenlő voltát szemléltető ábra. A pályagörbe s a hodográf, valamint az időbeli lefolyás: ez a kép kinematikailag kimerítő. Ami a dinamikát illeti, a gimnáziumi tankönyv megállapítja: "A bolygók mozgását leíró erőtörvény a Kepler-törvényekből levezethető. Kepler fáradozott is ilyen törvény megalkotásán, azonban ilyen irányú munkája nem volt eredményes." Majd közli a távolság négyzetével fordítottan arányos gravitációs erő képletét. Körpálya esetére az egyetemi kísérleti fizika tankönyvben 4 megtalálható a levezetés. Egyszerűsége középiskolába illő; valójában a gimnáziumi tankönyv3 119. oldalán közölt 2. példa képletéhez fűzött egyetlen megjegyzéssel elintézhető lenne. Ebben a cikkben meg szeretnénk mutatni, hogy a bonyolultabb feladat, a távolság négyzetével fordítottan arányos erő törvényének megállapítása ellipszispályákra szintén elvégezhető olyan matematikai eszközökkel, amelyeknek számos középiskolás birtokában van. Megfontolásunk azon alapszik, hogy a Kepler-mozgás hodográfja kör: a sebességvektor végpontja körmozgást végez. A sebességvektor végpontjának a sebességét, azaz a gyorsulást határozzuk meg. Bizonyos bonyodalmat jelent, hogy ez a körmozgás nem egyenletes. A számítást gépiesen elvégezhetnénk a közvetett, az inverz és az implicit függvény deriválási szabályát felhasználva. Ezekre mindamellett nem, csupán a szögfüggvények differenciahányadosainak határértékeire hivatkozunk. Az olvasótól, aki gépiesebb tárgyalást szívesebben látna, a szerző elnézést kér: cikkét ebben az alakban beszélte meg tizenéves (ált. iskolás, kismatematikus) beszélgetőtársaival. Végül szeretné hangsúlyozni: félreértés volna, ha e cikkben bárki határozott javaslatot vagy konkrét kritikát látna. Utakat, lehetőségeket keresni és kipróbálni: csupán ennyi volt a cél. A 400 éve született Johannes Kepler műve minden bizonnyal egy nemzedékhez sem állott olyan közel, mint a miénkhez, mely tanúja lehetett az Űrkorszak eljövetelének. Akarjuk azt és következményeit a természetleírás sajátos nyelvén: a matematikáén is gyermekeinknek minél pontosabban és élményszerűbben megmagyarázni !
1. Az egyenletes körmozgásról. Kiindulásképpen idézzük fel adott körpályához kötött tömegpont (anyagi részecske) mozgását. A pálya legyen egységnyi sugarú kör:
|
|
(1.1) |
A tömegpont (jele legyen ![]() P) helyét meghatározhatjuk x, y Descartes-koordinátái segítségével. De jellemezhetjük a P0OP körív u hosszával is
(1. ábra); u egyben a P0OP középponti szög ív mértéke. Megadása az x, y koordinátákat egyértelműen meghatározza:
P) helyét meghatározhatjuk x, y Descartes-koordinátái segítségével. De jellemezhetjük a P0OP körív u hosszával is
(1. ábra); u egyben a P0OP középponti szög ív mértéke. Megadása az x, y koordinátákat egyértelműen meghatározza:
|
x = cos u, y = sin u. |
(1.2) |
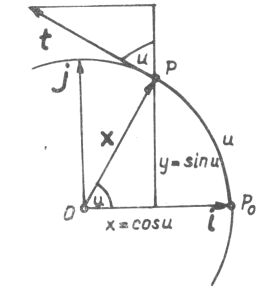
A tömegpont körpályáján egységnyi idő alatt fusson be egységnyi utat. A
![]() pályamenti sebesség tehát egyenlő eggyel.
A részecske adott pontba 2
pályamenti sebesség tehát egyenlő eggyel.
A részecske adott pontba 2
![]() idő múltán tér vissza; egyenletes körmozgással állunk szemben.
idő múltán tér vissza; egyenletes körmozgással állunk szemben.
Az O-t P-vel összekötő x helyzetvektort a síkbeli Descartes-koordinátarendszer tengelyei irányába mutató i, j egységvektorokkal az
| x = i cos u + j sin u | (1.3) |
alakban fejezhetjük ki. A sebesség vektora a pillanatnyi mozgásirányba, vagyis a körpálya P-beli érintőjének irányába mutat. Nagysága a pályamenti sebesség értékével egyenlő, ami esetünkben egy. Egységnyi hosszúságú, érintőirányú sebességvektorunkat t-vel jelöljük:
| t = - i sin u + j cos u. | (1.4) |
*
A t sebességvektort a fentiekben a körmozgás szemléletes képére hivatkozva nyertük. Hasznos lesz, ha eljárásunkat egybevetjük a sebesség határátmenet útján való kiszámításával. Az u szögnek megfelelő helyzetvektort jelöljük részletesebben x(u)-val. Növeljük meg u-t
![]() -val; x(u) ekkor x (u +
-val; x(u) ekkor x (u +
![]()
![]() x(u) +
x(u) +
![]() -re változik. A
-re változik. A
![]() /
/
![]() vektor a
vektor a
![]() elmozduláshoz tartozó átlagsebesség. Az i, j egységvektorokkal ez a
elmozduláshoz tartozó átlagsebesség. Az i, j egységvektorokkal ez a
|
|
(1.5) |
alakban fejezhető ki, ahol
|
|
(1.6) |
|
|
(1.7) |
Ha ![]() minden határon túl zérushoz közeledik, a (1.5) átlagsebesség mint határértékhez az (1.4) sebességvektorhoz tart:
minden határon túl zérushoz közeledik, a (1.5) átlagsebesség mint határértékhez az (1.4) sebességvektorhoz tart:
|
|
(1.8) |
|
|
(1.9) |
|
|
(1.10) |
2. A Kepler-mozgás származtatása körmozgásból merőleges vetítéssel. Az 1. szakaszban a körmozgást síkbeli Descartes-koordináták segítségével írtuk le. Vezessünk be most egy térbeli derékszögű koordinátarendszert; e1, e2, e3 legyenek a koordinátatengelyek irányába mutató egységvektorok.
Az i, j egységvektorok közül, amelyek segítségével a körpályát (1.3) alatt leírtuk, az előbbit válasszuk e1 -gyel egyenlőnek, az utóbbi pedig feküdjön e2 és e3 síkjában és e2-vel a
![]() szöget zárja be (
2. ábra):
szöget zárja be (
2. ábra):
|
|
(2.1) |
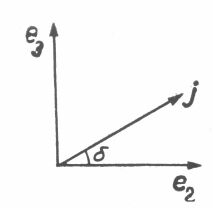
A következőkben az ![]() jelölést fogjuk használni; ekkor természetesen
jelölést fogjuk használni; ekkor természetesen
![]() . Az x helyzetvektor az el, e2, e3 egységvektorokkal az
. Az x helyzetvektor az el, e2, e3 egységvektorokkal az
|
|
(2.2) |
alakban fejezhető ki; el, e2, e3 mellett szorzóként a tömegpontnak új, térbeli koordinátarendszerünkre vonatkoztatott x, y, z koordinátái állnak:
|
|
(2.3) |
Vetítsük a körpályán keringő P pontot merőlegesen az xy síkra; P vetületét, melyet Q-val jelölünk az
|
|
(2.4) |
koordináták jellemzik (a harmadik koordináta természetesen zérus). Ellipszist kaptunk, melynek fél nagytengelye egy; E az excentricitás. Valóban: egyszerűen meggyőződhetünk arról, hogy a Q pontnak az
![]() , O és -
, O és -
![]() , O síkbeli Descartes-koordinátájú gyújtópontoktól mért távolságösszege const. (= 2). Megjegyezzük, hogy a (2.4) ellipszist az (1.2) körből y irányú,
, O síkbeli Descartes-koordinátájú gyújtópontoktól mért távolságösszege const. (= 2). Megjegyezzük, hogy a (2.4) ellipszist az (1.2) körből y irányú,
![]() arányú zsugorítással is. megkaphattuk volna. A vetítéssel való származtatás mindamellett a következők szempontjából előnyösebb.
arányú zsugorítással is. megkaphattuk volna. A vetítéssel való származtatás mindamellett a következők szempontjából előnyösebb.
*
A pályamenti sebesség állandó volta a vetítéskor veszendőbe megy. Jellemezhető azonban az egyenletes körmozgás olyan tulajdonsággal is, amit a merőleges vetítés nem ront el. Miközben a P pont körpályáján u hosszúságú ívet fut be, az x vektor u/2 területű körcikken seper végig. A (2.4) ellipszispályán haladó Q pont helyzetvektora által kisepert terület ezen körcikk területének
![]() -szorosa. (Bármely, az i, j vektorok síkjában fekvő T területű síkidomot merőlegesen vetítve az el, e2 síkra, T
-szorosa. (Bármely, az i, j vektorok síkjában fekvő T területű síkidomot merőlegesen vetítve az el, e2 síkra, T
![]() területű síkidomot kapunk.) Ha a P pont által megtett u út, mint feltettük, arányos az idővel, úgy az időegység alatt végigsepert terület, a területi sebesség, ugyancsak állandó. Az ellipszispályán haladó Q pont területi sebessége, vagyis az O-ból Q-ba mutató helyzetvektor által egységnyi idő alatt végigsepert terület, mely - mint láttuk - az előbbinek
területű síkidomot kapunk.) Ha a P pont által megtett u út, mint feltettük, arányos az idővel, úgy az időegység alatt végigsepert terület, a területi sebesség, ugyancsak állandó. Az ellipszispályán haladó Q pont területi sebessége, vagyis az O-ból Q-ba mutató helyzetvektor által egységnyi idő alatt végigsepert terület, mely - mint láttuk - az előbbinek
![]() (= állandó)-szorosa, ennek következményeképpen szintén konstans.
(= állandó)-szorosa, ennek következményeképpen szintén konstans.
*
A Q pont tehát ellipszispályán kering, mint a bolygók az I. Kepler-törvény szerint. A Q pont
mozgása és a bolygómozgás azonban eltérő tulajdonságú abban a tekintetben, hogy míg az első esetben a Q pontnak az ellipszis O középpontjára vonatkoztatott területi sebessége konstans, az utóbbi esetben a Nap által elfoglalt N gyújtópontból a bolygóhoz vont vezérsugár az, ami - a II. Kepler-törvény szerint - egységnyi idő alatt állandó nagyságú területen seper végig.
Módosítsuk modellünket oly módon, hogy Kepler II. törvényét is helyesen tükrözze vissza. Először a körmozgást végző P pontot vesszük szemügyre. A 3. ábrán a körpályával együtt ábrázoltuk (2.4)
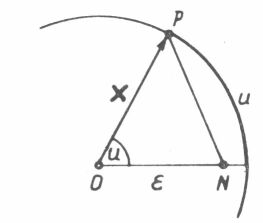
ellipszisünk jobboldali N gyújtópontját is (mely az x tengelyen fekszik s így benne van a körpálya síkjában). Az O-t P-vel összekötő x vektor mellett az N-től P-hez vont egyenes szakaszt is láthatjuk. Nevezzük ezt röviden NP vezérsugárnak.
Tudjuk: u hosszúságú ívdarab befutása közben az x vektor u/2 területű körcikken seper végig. Mekkora az a terület, amelyet eközben az NP vezérsugár súrol? Ezt oly módon kapjuk, hogy a körcikk u/2 területéből levonjuk az ONP háromszög
![]() területét. Az egyenletes körmozgást azzal jellemeztük, hogy az u ívhossz, vagy az x által súrolt u/2 terület az idővel arányosan nő. Ehelyett most új feltevést teszünk: legyen az NP vezérsugár által végigsepert terület arányos az idővel. Eszerint
területét. Az egyenletes körmozgást azzal jellemeztük, hogy az u ívhossz, vagy az x által súrolt u/2 terület az idővel arányosan nő. Ehelyett most új feltevést teszünk: legyen az NP vezérsugár által végigsepert terület arányos az idővel. Eszerint
![]() állandószorosa a t időnek; az állandót
állandószorosa a t időnek; az állandót ![]() -vel jelölve írhatjuk:
-vel jelölve írhatjuk:
|
|
(2.5) |
![]() ahol T az az idő, amely alatt u zérusról
ahol T az az idő, amely alatt u zérusról
![]() -re nő (periódus vagy keringési idő).
-re nő (periódus vagy keringési idő).
Ez annak feltétele, hogy az NP vezérsugár által súrolt terület arányos legyen az idővel. Az N-től Q-hoz vont vezérsugár által végigsepert terület ennek az xy síkra vetett merőleges vetülete. Mivel vetítéskor a terület
![]() (= const.)-szorosára változik, az új feltevés folytán a modell a kívánt módon módosult: ellipszispályáján Q a II. Kepler-törvénnyel összhangban kering.
(= const.)-szorosára változik, az új feltevés folytán a modell a kívánt módon módosult: ellipszispályáján Q a II. Kepler-törvénnyel összhangban kering.
A (2.5) összefüggés a Kepler-féle időegyenlet.
3. A Kepler-mozgás hodográfja. Határozzuk meg a körpályán. keringő P tömegpont pályamenti sebességét Kepler időegyenlete alapján. Az u szögnek megfelelő t időt jelöljük részletesebben t(u)-val. Növeljük meg u-t
![]() -val; t(u) ekkor t(u +
-val; t(u) ekkor t(u +
![]() )-ra nő. A
)-ra nő. A
![]() hányados, ahol
hányados, ahol
![]() , a
, a
![]() megváltozáshoz tartozó átlagos pályamenti sebesség. A pályamenti sebesség adott ponthoz (u-hoz, t-hez) tartozó értékét a
megváltozáshoz tartozó átlagos pályamenti sebesség. A pályamenti sebesség adott ponthoz (u-hoz, t-hez) tartozó értékét a
![]() határátmenet szolgáltatja.
határátmenet szolgáltatja.
Ha u-t ![]() -val megnöveljük, (2.5) baloldala
-val megnöveljük, (2.5) baloldala
![]() -val, a jobboldal
-val, a jobboldal
![]() -vel nő;
-vel nő;
![]() -vel osztva kapjuk:
-vel osztva kapjuk:
|
|
(3.1) |
Végezzük el a ![]() határátmenetet; (1.10) tekintetbevételével kapjuk:
határátmenetet; (1.10) tekintetbevételével kapjuk:
|
|
(3.2) |
(A t idő szerint elvégzett differenciálást olykor pont segítségével is jelezzük.)
A (3.2) pályamenti sebességgel megszorozva az (1.4) érintőirányú egységvektort, megkapjuk a P tömegpont sebességvektorát. Ezt w-vel fogjuk jelölni:
![]() Az (1.4), (2.1), (3.2) képletek alapján, az
Az (1.4), (2.1), (3.2) képletek alapján, az
![]() jelölés felhasználásával írhatjuk:
jelölés felhasználásával írhatjuk:
|
|
(3.3) |
A 2. szakaszban a P pontot merőlegesen projiciáltuk az xy síkra; Q, melyet ily módon kaptunk, a (2.4) ellipszispályán Kepler-mozgást végez. A Q pont sebességét v-vel fogjuk jelölni. A v sebességvektor a (3.3)-mal megadott w vektor vetülete az xy síkra. Az utolsó, e3-mal arányos tagot elhagyva kapjuk:
|
|
(3.4) |
Innen a derékszögű sebességkomponensek nyomban leolvashatók:
|
|
(3.5) |
A sin u, cos u szögfüggvényeket kiküszöbölve kör egyenletét kapjuk (feltéve, hogy
![]() ):
):
|
|
(3.6) |
Ez a Kepler-mozgás hodográfja. A kör sugara
![]() , középpontja az ordinátatengelyen van
, középpontja az ordinátatengelyen van
![]() magasságban (
4. ábra)
magasságban (
4. ábra)
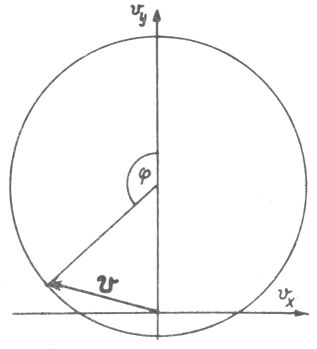
Hasznos bevezetni a ![]() szöget a
szöget a
|
|
(3.7) |
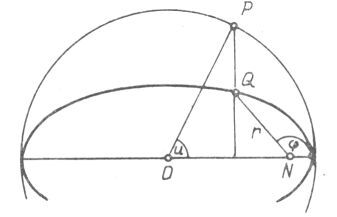
összefüggések segítségével; ![]() az ellipszispálya N gyújtópontját a Q ponttal összekötő vezérsugár,
az ellipszispálya N gyújtópontját a Q ponttal összekötő vezérsugár,
![]() pedig a vezérsugár azimutszöge
(5. ábra). A csillagászok
pedig a vezérsugár azimutszöge
(5. ábra). A csillagászok
![]() -t valódi anomáliának nevezik; u az excentrikus
-t valódi anomáliának nevezik; u az excentrikus
![]() közepes anomália. A vezérsugár az excentrikus anomália segítségével (2.4) alapján az
közepes anomália. A vezérsugár az excentrikus anomália segítségével (2.4) alapján az
|
|
(3.8) |
alakban fejezhető ki. A (3.7) képletek helyett írható:
|
|
(3.9) |
A (3.9) összefüggések megfordítása:
|
|
(3.10) |
Ez utóbbi összefüggések közül az elsőt (3.8)-ba helyettesítve a pályaellipszis polárkoordinátás egyenletét kapjuk:
|
|
(3.11) |
A valódi anomáliát meghatározó (3.9) egyenletek segítségével a (3.5) sebességkomponenseknek a
|
|
(3.12) |
egyszerű alakot adhatjuk. A hodográf új paraméteres előállítását kaptuk. A
![]() szög szemléletes jelentését a
4. ábra mutatja.
szög szemléletes jelentését a
4. ábra mutatja.
4. A Newton-féle gravitációs törvény. Határozzuk meg a v vektor végpontjának sebességét, vagyis: a Kepler-mozgást végző Q pont gyorsulását. Ismét körmozgással van dolgunk, csakhogy ez a körmozgás nem egyenletes.
Legyen ![]() és növekedjék a
és növekedjék a
![]() valódi anomália
valódi anomália
![]() idő alatt
idő alatt
![]() -vel. A
-vel. A
![]() differenciahányados komponensei (3.12) alapján :
differenciahányados komponensei (3.12) alapján :
|
|
(4.1) |
A ![]() /
/
![]() "átlagos szögsebesség" meghatározását megnehezíti, hogy
"átlagos szögsebesség" meghatározását megnehezíti, hogy
![]() -t nem tudjuk egyszerű, zárt alakban t segítségével kifejezni. Könnyen megadható azonban a (3.9) vagy a (3.10) képletek közül az első alapján
-t nem tudjuk egyszerű, zárt alakban t segítségével kifejezni. Könnyen megadható azonban a (3.9) vagy a (3.10) képletek közül az első alapján
![]() és u között a
és u között a
|
|
(4.2) |
összefüggés; u kapcsolatát t-vel a (2.5) Kepler-egyenlet fejezi ki. A keresett "szögsebességet" írjuk fel ezért a
|
|
(4.3) |
alakban. A ![]() differenciahányadost (3.1) alatt meghatároztuk. Még
differenciahányadost (3.1) alatt meghatároztuk. Még
![]() kiszámítása van hátra.
kiszámítása van hátra.
Az ![]() megnövekedett értékek között ugyancsak fennáll (4.2):
megnövekedett értékek között ugyancsak fennáll (4.2):
|
|
(4.4) |
Vonjuk le (4.2)-t (4.4)-ből; ![]() -val osztva, csekély átalakítás után kapjuk:
-val osztva, csekély átalakítás után kapjuk:
|
|
(4.5) |
Végezzük el most a ![]() határátmenetet. Ismerni kívánjuk a (4.1) differenciálhányadosok határértékeit, azaz a dv/dt gyorsulás komponenseit. Vegyük tekintetbe (1.9)-et és (1.10)-et, továbbá a (4.5)-ből (3.8) és (3.10) - [vagy (3.9) és (3.11)] figyelembevételével kapott
határátmenetet. Ismerni kívánjuk a (4.1) differenciálhányadosok határértékeit, azaz a dv/dt gyorsulás komponenseit. Vegyük tekintetbe (1.9)-et és (1.10)-et, továbbá a (4.5)-ből (3.8) és (3.10) - [vagy (3.9) és (3.11)] figyelembevételével kapott
|
|
(4.6) |
valamint a (3.2), (3.8) egyenletekből következő
|
|
(4.7) |
relációt; (4.3)-at is tekintetbe véve, (4.1) határértékére kapjuk:
|
|
(4.8) |
Ugyanez vektoregyenletté összefoglalva:
|
|
(4.9) |
ahol r° az N gyújtópontból a Q tömegpont felé mutató egységvektor. Megkaptuk az eredményt: a Kepler-mozgást végző tömegpont gyorsulása - megfelelően Newton gravitációs törvényének - fordítva arányos a rádiuszvektor négyzetével.
Megjegyzendő, hogy a (2.4) vagy (3.11) pályaellipszis fél nagytengelyét egynek választottuk. Ha nem így teszünk, a végeredményben az ellipszis a fél nagytengelye is fellép:
|
|
(4.10) |
Az ![]() tényező
tényező ![]() -tel egyenlő, s ez Kepler III. törvénye szerint a Naprendszer minden bolygójára ugyanaz az érték.
-tel egyenlő, s ez Kepler III. törvénye szerint a Naprendszer minden bolygójára ugyanaz az érték.
_________________________________
1 Fizikai Szemle 20, 13 (1970 január).
2 Fizikai Szemle 11, 248 (1961 augusztus).
3 Fizika a gimnáziumok III. osztálya számára, Tankönyvkiadó, Budapest.
4 Dr. Budó Ágoston Dr. Pócza Jenő, Kísérleti Fizika I. kötet, Tankönyvkiadó, Budapest, 1962. 89. o.