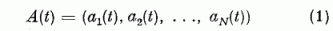
Fizikai Szemle honlap |
Tartalomjegyzék |
Zimányi József
Központi Fizikai Kutató Intézet,
Budapest
Az idegrendszer kutatásának egyik alapproblémája annak megmagyarázása, hogy hogyan szerveződik egy hatékonyan működő hálózatba a központi idegrendszerben levő óriási számú neuron. (Az ember központi idegrendszerében levő neuronok számát 3 × 1010-re tehetjük. Egy-egy neuron átlagosan mintegy 103 neuronnal van kapcsolatban.) E hálózat pontos megadásához olyan sok információra van szükség, hogy kizártnak tekinthetjük a teljes információ DNS-ben kódolt genetikai átvitelét. Genetikusan csak a hálózat globális vonásai lehetnek meghatározottak. Szükséges tehát feltételezni, hogy a neuronhálózatnak rendkívül hatásos önszerveződő képessége van, aminek révén az eredetileg véletlenszerűen, csak statisztikusan megadott módon kapcsolódó neuronok egy hatékony, koherensen működő hálózattá alakulnak.
A következőkben egy modell-rendszer vizsgálata kapcsán rámutatunk ezen önszerveződés egy lehetséges módjára. A modellünk [1] egymással kölcsönösen gátló kapcsolatban álló neuronokból áll. Az egyes neuronok aktivitását egy egyszerű, általános tanuló elv szabályozza. Megmutatjuk, hogy ez a rendszer, véletlen eloszlásban érkező ingerek hatására, bármílyen kezdő állapotból ugyanabba a jól meghatározott állapotba fejlődik.
A modellünkben felírt neuron egyenlet és memória egyenlet a [2]-ben javasolt egyenletekhez hasonló. A neuronhálózatok tárgyalásának bevezető jellegű összefoglalását [3]-ban írtuk le.
(Egy impulzus hossza körülbelül egy ezred másodperc). Így a párhuzamos szálak kötegének egy metszetében "villogó ábrákat" észlelhetnénk (ez az elrendezés hasonló a független impulzusokat szállító optikai üvegszál köteghez). A párhuzamos szálakat megszámozzuk 1-től N-ig. A t időben a köteg keresztmetszetében észlelhető ábrát az A(t) vektorral adjuk meg. Az A(t) elemei a 0 vagy 1 értéket veszik fel aszerint, hogy a megfelelő párhuzamos szál aktív vagy inaktív volt-e a t időpillanatban :
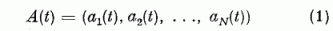
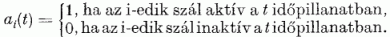
Ezek az ábrák jelennek meg a P neuronok bemenetein. (A kisagyban a Purkinje sejtek valóban ilyen ábrákat "figyelnek" dendritjeik segítségével). A bemeneti helyek a párhuzamos szálak és a
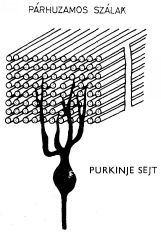
1. ábra A kisagybeli Purkinje-sejt és a párhuzamos szálak kapcsolatának vázlatos képe
P neuron dendritje közötti szinapszisok. Minden szinapszishoz egy erősséget rendelünk.
A k-ik párhuzamos szálat az i-ik neuronhoz kapcsoló szinapszis erősségét jelöljük
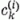 -val. Egy
ehhez a szinapszishoz érkező impulzus a P neuron axon dombjának feszültségét
Δv(t)-vel növeli. A szinapszis erősségét ezzel a potenciál változással
definiáljuk:
-val. Egy
ehhez a szinapszishoz érkező impulzus a P neuron axon dombjának feszültségét
Δv(t)-vel növeli. A szinapszis erősségét ezzel a potenciál változással
definiáljuk:

Az i-ik P neuron gerjeszthetőségét a

érzékenységi vektorral karakterizálhatjuk. Az i index az i = 1, 2, ... , M értékeket veheti fel, ahol is
M a P neuronok száma. Természetesen igen sok
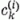 zérus, mert egy P neuron nem
csatlakozik az összes párhuzamos szálhoz.
zérus, mert egy P neuron nem
csatlakozik az összes párhuzamos szálhoz.
Egy neuron működését a következő módon írjuk le.
A neuron v(i)(t) gerjesztési potenciálja, ha egyéb input nem érkezik, időben exponenciálisan csökken λ csökkenési állandóval. (A gerjesztési potenciált a neuron nyugalmi potenciáljától számítjuk).
A neuron aktívvá válik, ha potenciálja az axon dombon meghaladja az s(i) küszöb értéket. Ekkor a neuron egy τ hosszúságú, nem csökkenő impulzust emittál az axonja mentén. A P neuront gátló típusnak tekinthetjük, így axonjának minden szinaptikus csatlakozásánál gátló hatást fejt ki (azaz nem növeli, hanem csökkenti a hozzá csatlakozó neuron potenciálját). Ezt az aktivitást a w(i)(t) függvénnyel írjuk le:
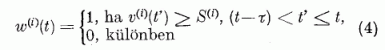
A P neuron axonjának szinaptikus kapcsolata van a többi P neuronnal. Egy ilyen kapcsolat
erősségét 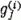 -vel jelöljük;
-vel jelöljük;
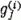 -t azzal a potenciál csökkenéssel
definiáljuk, mely az i-edik P neuronon jön létre, akkor amikor a j-ik P neurontól gátló impulzus
érkezik.
-t azzal a potenciál csökkenéssel
definiáljuk, mely az i-edik P neuronon jön létre, akkor amikor a j-ik P neurontól gátló impulzus
érkezik.
A fenti diszkusszió alapján a neuron potenciál időbeli változását leíró egyenlet, mely megadja a potenciál t + τ időben felvett értékét a t időben mérhető adatok segítségével, így írható:
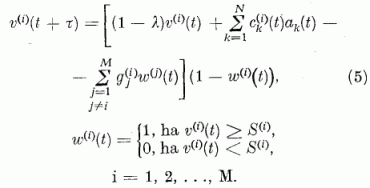
Ezek az egyenletek a neuron egyenletek. Azt mutatják, hogy a neuron potenciál a t + τ időben úgy kapható meg, hogy a t időbeli potenciálból levonunk egy kis vesztességi tagot, -λv(i)(t), hozzáadjuk a párhuzamos szálakon érkező gerjesztés hatását, ∑ckak; levonjuk a többi P neurontól érkező gátlások hatását megadó tagot, ∑-gjw(i). Végül egy szorzófaktort alkalmazunk, (1-w(i). Ennek a tényezőnek a hatására az impulzus-emisszió (tüzelés) után a neuron potenciál visszaáll az alapértékére és ott is marad a refrakter idő Tr = τ (kb. 1 ms) alatt. A refrakter idő alatt a neuron nem gerjeszthető. Áttekinthetőbbek az egyenletek, ha a gerjesztési potenciált a küszöb potenciál egységekben fejezzük ki. Definiáljuk tehát a relatív gerjesztettséget a következő módon:
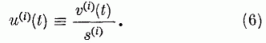
Az u(i)(t) relatív gerjesztettség időbeli változására vonatkozó egyenletet az 5. egyenletből kapjuk úgy, hogy annak mindkét oldalát elosztjuk a s(i) küszöb feszültséggel:
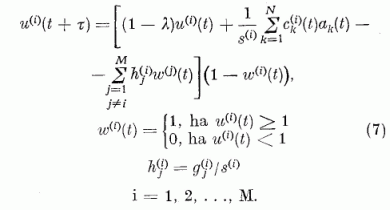
A neuron egyenletnek ezt az alakját használjuk a továbbiakban.
Amikor a neuron hálózatnak az A(t) vektorral jellemzett ábrák "villogására" adott közvetlen válaszát számoljuk, a szinaptikus erősségeket gyakorlatilag konstansoknak tekinthetjük. Egy hosszabb időskálán azonban ezek az erősségek is változnak és ezáltal a hálózat tanulása lehetségessé válik. A szinapszis erősségének változására a Hebb féle tanulási elvhez [4] hasonló elvet használunk. Ezt a tanulási elvet a következőkben fogalmazzuk meg:
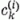 erősségű szinapszison érkező
ak(t) gerjesztést a P neuron tüzelése követi
(w(i) = 1), akkor ez a szinapszis erősödik (a hatásos gerjesztések erősítik a
szinapszist);
erősségű szinapszison érkező
ak(t) gerjesztést a P neuron tüzelése követi
(w(i) = 1), akkor ez a szinapszis erősödik (a hatásos gerjesztések erősítik a
szinapszist);
A fentiekben megfogalmazott tanulási elvet a szinaptikus erősségek időbeli változására vonatkozó következő egyenlettel foglaljuk össze:
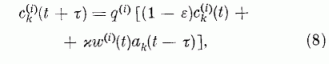
ahol a
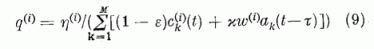
normálási faktor biztosítja, hogy a gerjesztő szinapszis erősségek összege ne változzon:

A 8. egyenletet memória egyenletnek nevezzük.
Az itt javasolt tanulási mechanizmus nincsen ellentmondásban Szentágothai [5] és Marr [6] conjunctionális tanulási elvével, hanem alesetként tartalmazza azt. Nevezetesen a conjunctionális tanulási elv azt feltételezi, hogy a párhuzamos szál és a Purkinje-sejt közti szinapszis akkor erősödik, ha a párhuzamos szálon érkező ingerrel egyidőben a kúszó roston is érkezik inger. Mivel azonban a kúszó roston keresztül jövő inger minden esetben tüzelésre kényszeríti a Purkinje-sejtet. a conjuctionális tanulásnak ez a speciális esete az a) tanulási elv következményének is felfogható.
A 7. és 8. egyenletek meghatározzák a hálózat viselkedését adott bemenet esetén, ha a kezdeti értéket megadjuk. Tegyük fel, hogy a szinaptikus erősségek kezdőértékei véletlenszerűen oszlanak el ("tanulatlan állapot"). A parallel szálakon egy megadott A1 ábra villan fel többször egymás után. Ennek hatására az összes P neuron gerjesztettsége növekedni kezd. A gerjesztettség abban a neuronban - jelöljük ezt P(1)-gyel - növekszik a leggyorsabban, amelyiknek szinaptikus erősségeloszlásával képezett ∑ckak gerjesztési összeg a legnagyobb. Ez a P neuron éri el először a küszöb gerjesztést, amikor is tüzelni fog. A tanulási mechanizmus révén ennek a P neuronnak azok a szinapszisai fognak erősödni, amelyeken inger érkezett. Ennek a neuronnak a ∑ckak gerjesztési összege megnövekszik az A1 ábrára. Így a P(1) neuron egyre érzékenyebb lesz az A1 ábrára. Eközben P(1) többi, impulzust nem közvetített szinapszisai gyengülnek, így P(1) egyre kevésbé lesz érzékeny a másfajta ábrákra. Ha a P neuronok nem volnának kölcsönös gátló kapcsolatban, akkor ugyanez a folyamat a többi neuront is érzékenyítené az A ábrára. Azonban a kölcsönös gátlás révén a P(1) neuron, amikor elérte a küszöb szintre való gerjesztettséget, a többi P(1) neuronra gátló impulzust ad, és ezzel csökkenti azok gerjesztettségét. Így a többi P(i) neuronnak egyre hosszabb és hosszabb időre lesz szükséges ahhoz, hogy az A1 ábrára tüzeljen, és végül az A1 ábrára már egyáltalán nem fognak tüzelni, érzéketlenné válnak A1-re.
Ugyanez a tanulási folyamat a különböző P(i) neuronokat különböző Ai ábrákra teszi érzékennyé.
A fentieket összegezve a következóket állapíthatjuk meg. Egy neuron hálózatban, amelyben a szinaptikus kapcsolatok kezdetben véletlenszerűen, csak statisztikus törvények által meghatározottan voltak eloszolva, a különböző P neuronok
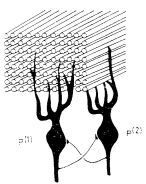
2. ábra Az egymást kölcsönösen gátló két P neuron rendszer vázlatos képe
a párhuzamos szálakon át érkező különböző ábrákra szelektív érzékenységet fejlesztenek ki. Ez a fejlődés a kölcsönös gátlás és egy egyszerű, minden neuronra érvényes tanulási mechanizmus következményeként jön létre.
A neuron hálózat kvalitatív analízise plauzibilis eredményre vezetett. Ennek megerősítésére és a hálózat önszervező tulajdonságának mélyebb megértésére kvantitatív analízist írunk le a következőkben. Egy nagy számú neuronból álló rendszer részletes vizsgálata, ahol minden neuronnak több tízezer szinapszisa van meghaladja a ma ismert matematikai módszerek teljesítőképességét. A következőkben két, egymással kölcsönös gátló kapcsolatban álló P neuront fogunk vizsgálni (2. ábra ). Mindegyik P neuron sok szinapszissal kapcsolódik a párhuzamos szálakhoz. A ∑ckak összeg kiszámításához azonban egy további egyszerűsítést is bevezetünk: a rendszernek két orthogonális ábrára vonatkozó adaptív tulajdonságát vizsgáljuk. (Két ábrát orthogonálisnak nevezünk, ha az ábravektoruk skaláris szorzata nulla.)
Legyen a kiválasztott két P neuron egymás mellett, így a parallel szálaknak ugyanarról a területéről kapják mindketten a gerjesztést. Osszuk fel a két P neuron "látóterén" (perceptív területén) átmenő párhuzamos szálakat két egyenlő, diszjunkt halmazra. Jelöljük e két halmazt Gx és Gy-nal. Mindegyik n szálat tartalmaz. Egy általános információ során a Gx halmazból nx, a Gy halmazból ny lesz aktív. Ezek átlagos gerjesztő hatását a két P neuronra megkapjuk, ha a gerjesztési összeget két részre bontjuk.
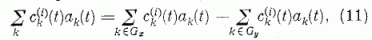
Itt a két összegezés a Gx, illetve a Gy halmazhoz tartozó párhuzamos szálakra való összegezést jelöli. Definiáljuk az egyes halmazokban az átlagos szinaptikus erősséget a következő módon:
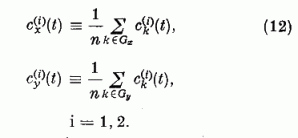
Ha a szinaptikus erősségeket ezen átlagokkal közelítjük, a gerjesztési tag nagyban egyszerűsödik:
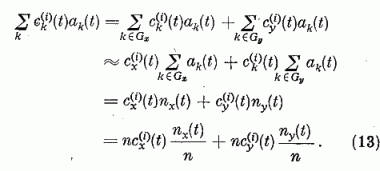
Definiáljuk továbbá az effektív érzékenységi vektort,
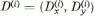 , és az effektív ábra vektort,
B = (Bx, By), a következő kifejezésekkel:
, és az effektív ábra vektort,
B = (Bx, By), a következő kifejezésekkel:
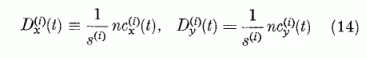
és
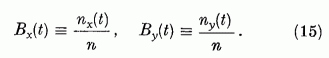
Ezekkel a definíciókkal a gerjesztési tagot így írhatjuk:
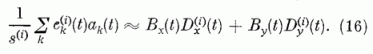
A normálási feltétel most a
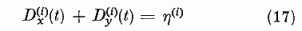
alakot ölti.
Abból a célból, hogy az eredményeket jól lehessen szemléltetni, a D(i)(t) és B(t) vektorokat polár koordinátákkal fogjuk megadni:
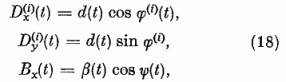
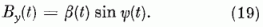
Mivel a normálási feltétel egy összefüggést ír elő 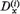 és
és 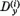 között, a φ(i)
érzékenységi szög teljesen megadja a P(i) neuron érzékenységi állapotát.
között, a φ(i)
érzékenységi szög teljesen megadja a P(i) neuron érzékenységi állapotát.
Összegezzük az eddigieket. A modell hálózatunk két P neuronból áll, melyek egymást kölcsönösen gátolják. A P neuronokat a 14. egyenletben megadott érzékenységi vektorokkal jellemezzük. A párhuzamos szálakon érkező gerjesztést a 15. egyenlettel definiált két komponensű effektív ábra vektorral adjuk meg. A teljes redukált hálózatot a 3. ábra mutatja. E hálózat működését leíró neuron
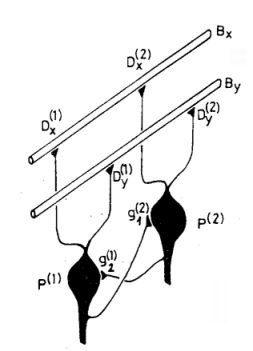
3. ábra A redukált modell képe.  és
és  az effektív szinapszis erősségek,
az effektív szinapszis erősségek,  és
és  a gátló szinapszisok erősségei, Bx és By a gerjesztő ábra komponensei.
a gátló szinapszisok erősségei, Bx és By a gerjesztő ábra komponensei.
egyenletek, melyeket a 16. egyenletnek a 7. egyenletbe való helyettesítésével kapunk, a következők:
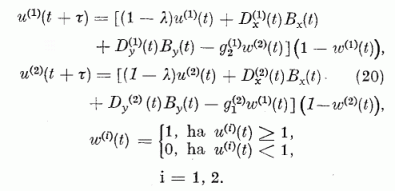
A modell memória egyenletét úgy kapjuk meg hogy a 8. egyenletet összegezzük
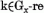 -re és
-re és
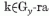 -ra, majd elosztjuk a kapott
egyenleteket (i)-vel :
-ra, majd elosztjuk a kapott
egyenleteket (i)-vel :
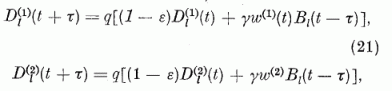
ahol
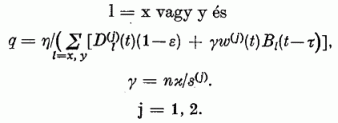
E modell hálózat viselkedésének tanulmányozására számológép programot készítettünk. 120 különböző bemenő ábrát alkalmaztunk. A β ábra erősségnek a β = 0,2, 0,3 és 0,4 értékeket adtuk. A Ψ ábra szögeknek 40 különböző értéket adtunk a [0, 90°] intervallumban. Az így nyert 120 ábrát véletlen sorrendbe állítottuk. Egy-egy ábrát 100-szor kapcsoltunk rá a hálózat bemenetelére mielőtt áttértünk a következő ábrának a bekapcsolására. A φ(1)(t) és φ(2)(t) érzékenységi szög változását minden ábra "felvillantása" után meghatároztuk. A φ(1)(t), φ(2)(t) számpárost minden 12 000. ábra felvillantása után kinyomattuk. Egy-egy ilyen számpárost egy-egy pont jelöl a 4. ábrán. Egy ilyen kinyomtatás után a számítás tovább folytatódott.
Mivel az érzékenységi vektorok normáltak, a. két P neuronból álló rendszer érzékenységét teljesen leírja a két, φ(1)(t) és φ(2)(t) érzékenységi szög. Így egy pont a (φ(1), φ(2)) "érzékenységi fázis síkon" (4. ábra) teljesen megadja a modell érzékenységi állapotát, és az út, amelyen ez a pont halad, az érzékenységnek a tanulás folyamán létrejövő változását adja meg. A 4. ábrán az útra rajzolt nyíl a fejlődés irányát mutatja. Két szomszédos pont közt eltelt idő mindig azonos, éspedig a 12 000 ábra "felvillantásának" megfelelő idő. A különböző utak különböző kezdő érzékenységnek felelnek meg. A paramétereknek az értéke e számítás során a következő volt:
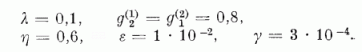
A rendszer szimmetrikus a két P neuronra vonatkozóan, és ezért a rendszer viselkedése a I. tartományban tükörképe a II. tartománybeli viselkedésének. (4. ábra).
Az egyszerűsített modell numerikus analízise alátámasztja a hálózat kvalitatív analízise során nyert következtetéseket. A 4. ábra világosan mutatja, hogy a rendszernek fix pontjai vannak az "érzékenységi állapot fázis síkon". Ez azt jelenti, hogy a rendszer tetszőleges kezdeti állapotból mindig ugyanabba a "tanult állapotba" szervezi magát a véletlenszerű eloszlásban érkező ingerek hatására. Ebben a tanult állapotban a két-P-neuron rendszer felosztja az ábrateret két egyenlő részre, és az egyik P neuron csak az egyik részhez, a másik neuron csak a másik részhez tartozó ábrákra lesz csak érzékeny. (Egy kis szakaszon, a két rész határán, minkét neuron érzékelheti az ábrát (lásd az 5. ábrát).
A bemutatott matematikai analízisből beláttuk, hogy tetszőleges kezdeti szinapszis erősség eloszlással bíró P neuronok esetén is a rendszer mindig ugyanabba a fix tanult állapotba szervezi magát. Ebben az állapotban diszkriminálni képes a beérkező gerjesztések között. A rendszernek ez az önszervező képessége a kölcsönös gátló kapcsolat és a neuron sejtre a 8. egyenletben megfogalmazott egyszerű tanulási elv következménye.
Végezetül megjegyezzük, hogy a fentiekben leírt önszervező képesség akkor is létrejön, ha a kölcsönös gátlás interneuronokon keresztül valósul meg. Úgyszintén megjegyzendő, hogy ez az önszerveződés nem zárja ki a "tanító segítségével történő
tanulást", azaz a P neuronnak a kúszó rost segítségével létrejövő tanulását. A két mechanizmus egymástól függetlenül vagy éppen egymással együttműködve is működhet.
________________________
Előadás az .MTA 1980. évi közgyűlése alkalmából rendezett biofizikai ülésszakon.