VALÓSÁG.....MODELLEK.....GYEREKEK

Eric M. Rogers
Princeton University and Nuffield Foundation
O-Level Project

Itt van három irodalmi idézet, hogy az olvasó eltűnődjön, míg az új gépek szédületes tempóban járják saját útjukat.

Az első egy asztronómiai tény költői leírása. Modell ez? A tudósok "magyarázat"-igényét nem elégíti ki: de leírja-e a jelenséget? Alakít-e ki drámai sikerrel képet az emberi elmében? Ha igen, akkor gyarapítja-e a tudást? A második az oktatás legmélyebb kérdését teszi fel, és Jób a fejezet további részében - elvárásomnak megfelelően - elkerüli a világos állásfoglalást, végezetül csak egy általános vallási kijelentést ad pozitív válaszként.

A harmadik mélyen gyökerező, intellektuális és lelki harcunkra emlékeztet bennünket. Itt kell feltennem egy kérdést a számítógépekről. Bizonyos, hogy időt nyerünk velük, összefoglalhatják és analizálhatják tudásunk szövevényes aspektusait; a hallgatóknak helyes választ tudnak adni bőséges memóriájukból. De képesek-e támogatni és előbbre vinni az általunk oly komolyan vett és fontosnak tekintett kutatást?

Niels Bohr

A kutatás néhány vonatkozását nagyban előre vitte Niels Bohr, ki oly nyilvánvalóan tudott mélyen gondolkodni. Ebben az évben van születésének centenáriuma; a visszaemlékezésekhez egy rövid történettel szeretnék hozzájárulni és az előadás végén bemutatok egy modellt, melyet ő javasolt a Nagy Komplementaritási Elvének illusztrálására.

A történet. Emlékszem Bohr egy Cambridge-i látogatására, ahol a kémiai elemekről tartott előadást, megmutatva helyüket a Mengyelejev-táblázatban. Kezdte a H-val, két összeadással jutott el a He-hoz*. Azután a Li és így tovább..., megemlítve a már ismert, illetve várható tulajdonságaikat. Csodálatos előadás volt. Kísérleti tények vagy nagy sikerű sejtések voltak? (Nekem mindkettő.) De amint az idő haladt előre, és Bohr elemről elemre folytatta, egy óvatos pillantás az órára azt mutatta, hogy a Cavendish Laboratórium szemináriuma szokásos befejezéséig már csak pár perc van hátra; és Bohr még csak néhány elemmel volt kész. Az udvariasság azt diktálta, hogy maradjunk a radioaktív befejezésig. De egy perccel az óraütés előtt Bohr megállt és határozottan kijelentette: "A többi szisztematikus botanika."

Modellek és gyermekek

Az általunk készített - elképzelt - modellek lényeges elemei a 'Természet megértésének. De a gyerekek - sőt még az idősebb hallgatók is meglepődnek és csalódottak, hogy ha azt mondjuk nekik, hogy az általunk adott leírások: (csak) modellek. Fiatal korban az igazat várják, az "igazán valódi" leírását az atomoknak, ...molekuláknak, ...kristályszerkezetnek, ...sőt még a fekete lyuknak is. Ügyetlennek vagy szerencsétlen tudatlannak tartanak bennünket, amikor azt mondjuk, hogy csak modelleket és jobb modelleket tudunk nyújtani, hogy kifejezzük azokat a módozatokat, amiket a Természetben felismerni vélünk. Csak lassan fogadják el a görög filozófusok által "Első okok"-nak minősített fogalom megismerésének lehetetlenségét. Tehát óvatos terápia szükséges. Finomabban kell megközelíteni a problémát, még ha azt játékmodellekkel kezdjük is.

Játékmodellek

A játékok, olyanok mint az imádott "maci", vagy egy villanyvasút, jelentős motivációk gyermekkorban. Alkalmanként a játékmodell természettudományt tanít vagy tudományos kérdést vet fel. Például módosítsuk a játékvonat mozdonyát a következőképpen: szélesítsd ki kéményét és helyezz belé egy kis egyenáramú elektromágnest, mely egy szabadon mozgó dugattyút vesz körül. A dugattyú felső része sárgarézből, az alsó pedig vasból legyen. Tápláld a tekercset egy a kis vonatra helyezett telepről, de úgy helyezd a kapcsolót a sínre, hogy az csak rövid időre zárjon éppen akkor, amikor a vonat bemegy az alagútba. Mikor a mágnes begerjed, felrántja a dugattyút s az éles ütést mér egy sárgaréz golyóra, mely függőlegesen kilövődik. Nyugalomban levő vonatnál a golyó a kéménybe hullik. Ezt követően hadd fusson a vonat a pályán, melynek egy egyenes szakaszán legyen a mágneses kapcsoló és az alagút. A golyó ekkor parabola pályát leírva átrepülhet az alagút fölött és visszatér a kéménybe az alagút után. Futtassuk ezt karácsonykor, és engedjük feltenni saját kérdését a fizikáról. Csak egy-két játékmodellt kell megmutatnunk~és aztán azt mondani, hogy ez nem a tudomány magyarázásának része, (hanem) csak játék.

Tanításmodellek

Még kevésbé kielégítő, amikor azt mondjuk, hogyan írjuk le a Természetet modellekkel. Mégis fogjuk használni azokat meggyőzésre és oktatásra. Tálcán levő acélgolyók véletlenszerű mozgásban tarthatók: a tálca sarkainál ütögetve a falat láthatóvá tehetjük az ütközésüket, ezzel illusztrálva a gázban mozgó molekulákról való képünket. Az üveggolyók még jobbak lennének; nagyobbak, csaknem olyan rugalmasak és már megszokott játékok. Senki sem fogja azt hinni azután, hogy a levegőmolekulák, (ezen kis pöttöm, láthatatlan kis golyók) azon barátságtalan anyagból, acélból készültek. (És senki sem fogja azt hinni, hogy az U235-ös bomba egérfogókból vagy konyhai gyufából épül fel, jóllehet mindkettőben van olyan vonás, mely illusztrálhatja egy robbanáshoz vezető láncreakcióról alkotott általános képet.)

Modellek a Természet kifejezésére

Ezek egy matematikai formulától - néha teljesen új matematika - túlzottan reális megjegyzésig mint például, ha azt mondjuk, hogy hélium-atom egy gömbölyű golyó - terjednek. A "gömbölyűt" csak azért tesszük hozzá, hogy kifejezze szimmetriáját. A "golyó" alaposan félrevezető, mert a kezdőt arra csábítja, hogy megkérdezze "Mennyi az átmérője? "**

A matematikai formula - mint modell - érdeme egyszerűségében van. Noha ez gyakorlati előny, használatát ez teszi kétségessé egy fizikus számára. Például, ha megkérünk egy matematikust, hogy írjon le egy csillapított harmonikus mozgást, általában az

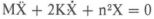
egyenletet kapjuk válaszul, holott a valóságban ritkán fordul elő olyan surlódás, amilyet a Stokes-törvény jelent, hacsak az objektum nem egy kis ködcsepp, vagy egy Millikan olajcsepp! A folyadékban levő súrlódás sokkal inkább v2-tel, semmint v-vel arányos, de az utóbbi esetben a differenciálegyenlet megoldása könnyebb!

A gömbölyű golyó közel áll hozzánk

Mind a fenőnek, mind a gyerekek - kivéve a csecsemőket -, ha egy szokatlan tárggyal (vagy gondolattal) találkoznak, megkísérlik úgy leírni, hogy valami megszokotthoz kapcsolják. Nincs csodálkozni való azon, hogy a héliumatomot gömbölyű golyónak nevezzük, jóllehet elővigyázatosabban azt kellene mondanunk, hogy az "olyan, mint egy gömbölyű golyó". Pszichológus kollégáinknak kitűnő demonstrációja van ezen emberi törekvés bemutatására. Építettek egy erősen eltorzított modellszobát, de belül úgy építették ki, hogy a megfigyelő azt higgye, hogy derékszögű. Ezen illúzióért a megfigyelőnek be kell kukucskálnia egy olyan lyukon át a szobába, melyhez a torzított kiépítést tervezték. A szoba hátsó fala magas és messze van az egyik oldalon és alacsonyodva közeledik a másik oldalhoz (lásd 1. ábra). Egy ember áll a magas oldali küszöbön: a megfigyelő kicsinek, törpének látja őt. Ezt követően az ember átsétál az alacsony, közelben levő ajtóhoz és kitölti az ajtónyílást, mint egy óriás. A megfigyelő inkább elhiszi, hogy az ember valami csoda folytán óriás méretűvé nőtt, semmint hogy elhiggye, hogy a szoba nem derékszögű, még akkor sem, ha ezt közlik vele. Még rosszabb, mikor a megfigyelő egy csatornát lát a szobában, ami látszólag lejt egyik oldalról a másikra. Egy kéz egy labdát helyez ebbe a csatornába és az "felfelé" gurul, azt a látszatot keltve, mintha mozgás közben növekedne. Gondolkodásunk megvéd bennünket az új, szokatlan dolgoktól. Ez olyan megszívlelendő figyelmeztetés fiatal fizikusok, illetve pszichológusok számára, hogy úgy vélem minden fizikusképző intézetben kellene lennie egy torzított szobának, még ha kartonpapírból csinálták is.

De vajon mit csinál egy csecsemő? Minden látványt és szót újnak talál, így aztán a tanulási folyamat közvetlen és lenyűgözően gyors kell, hogy legyen.

Térképek

Mit tehetünk annak érdekében, hogy a tanítási folyamat során a Természetről való ismereteink átadását szolgáló modellek elfogadhatóbbak legyenek. Kijelenthetjük, hogy "a játékmodellek nem reálisak; a Természet modelljei, kicsit olyanok, mint az atom, de nagyon hasznosak - és a legjobbak mit elérhetünk". Olyanok, mint a térképek; bár a térképet sokkal inkább gazdag elméleti alkotásnak, mintsem sajátos modellnek tekintem.

Ha hallgatóink otthonosak egy városban, ahol földalatti van, fölhasználhatjuk a vonaltérképet mely rendszerint stilizált - és a város busztérképét. Angliában ezt különösképp gyümölcsözőnek találom. Bemutatom a londoni földalatti többszínű térképét, amin a vonalak fel-le, jobbról balra, vagy éppen 45 °-os szögben futnak, valamint a busztérképet, ami szükségképpen követi az út kacskaringóit. Aztán megkérdezek egy 16 évesekből álló Nuffield osztályt "Melyik a helyes térkép?" (Vigyázok, nehogy plusz zavart okozzak azzal, hogy "igazi"-t mondok "helyes" helyett.) Egy vagy esetleg több hallgató is a következő kifogást emeli: "Attól függ, hogy mire akarjuk használni." Igen, és pontosan ez a helyzet agy. atom- és molekulamodellekkel is: egyszerű, rugalmas, szilárd golyó a korai kinetikus gázelméletben, ...egy egyenes pálya a ködkamra-képekben, ...no de a radioaktivitás?????

Bohr féle komplementaritás

Azon az alapon, ahogy egyfajta mérés kizárhat egy másikat - egymást páronként kölcsönösen kizáró esetek -, Bohr felállított egy általános elvet sok különböző alkalmazással. 'Tekintsünk két rövid tanmesét. Első tanmese. Tegyük fel, hogy van egy dobozkánk, olyasmi, mint egy gyufásskatulya, ami vékony, ciripelő hangot bocsát ki. Két embernek lehetősége van megvizsgálni, hogy felnyitás nélkül kiderítsék mi van benne. B., egy amatőr biológus meghallgatja és úgy dönt, hogy rovar van benne, olyan, mint egy tücsök. Miután ezt a döntést meghozta, tudományos kérdésfeltevésre képes, és ezekre válaszokat kap. Meghallgatja a ciripelés zenei hangjait és időtartamát, aztán megbecsüli (el tudjuk képzelni) a tücsök lábán levő barázdák számát és azok egymástól való távolságát. Ez még addig is elsegítheti, hogy kitalálja a bentlevő tücsök fajtáját. Ez az ő hipotézisére épülő jó tudományos feltevés, de azon való nagy felbuzdulásában, hogy a dobozba indirekt úton belelásson, nem veszi észre azt a kényszert, amit magára vett az első feltevés elfogadásával.

Ezenközben M., egy rádiómérnök, figyeli és hallgatja, majd úgy dönt, hogy egy kis tranzisztoros rádióoszcillátor van a dobozban. A doboz méretéből és a ciripelés hangmagasságából megbecsüli (el tudjuk képzelni) a ciripelést szabályozó kondenzátor adatait.

Ezt követően B. és M. összejönnek. Bár egyáltalán nem értenek egyet a magyarázatban, de abban megegyezik véleményük, hogy egy további kísérletet kell végezni. Még mindig nem nyithatják ki a dobozt, de engedélyt kapnak, hogy olajat öntsenek bele a sarkán levő kis repedésen keresztül. A ciripelés mélyebb hangon folytatódik. A biológus B. azt mondja "Pontosan az, amit vártam: nehezebben tudja mozgatni a viszkózus olajban lábait". A mérnök M. mondja: "Ez döntő. Olaj folyt a kondenzátorlemezek közé, az mindig növeli a kapacitást, s az pedig a zenei hangot mélyíti." Mindketten megerősödtek hitükben - és mindketten elfelejtik, hogy mérésüknek csak alapfeltevésük keretében van ilyen tanulsága.

Második tanmese: Egy ideges betétkönyv-tulajdonos, aki megtakarított pénzét bankba rakta, aggódik a pénze miatt, és meg akar győződni arról, hogy tényleg ott van-e biztonságban a bankban. Két módszerrel próbál meggyőződni erről:

1. ) Megnézi a rendszeres kamatfizetést és ebből arra következtet, hogy a banknál megvan a pénze.
2. ) Felidéződik egy gyermekkori emléke, mikoris zseblámpájával bekukucskált a malacperselybe, és időről időre bemegy a bankba követelni a pénz kiadását, hogy megnézze. A bank beleegyezik, de figyelmezteti, hogy így nem lesz kamat (a bank továbbá elmondja neki, hogy ha minden ügyfelüknek gyakran lenne ilyen kívánsága, akkor a bank nem tudna működni).

A betétkönyv-tulajdonos bármelyik módszert sikeresen alkalmazhatja, de egyiket használva a másik elveszti helyes ellenőrzőképességét. Át kell formálnia a bankszakmáról alkotott képét és meg kell tanulnia, hogy bár pénze biztonságban van, de nincs olymódon ott, mint készpénze a szalmazsákban.

Általános komplementaritás

A komplementaritást megtaláljuk intellektuális világunk főbb pontjain: a természettudományban, filozófiában, etikában - és az életben is. Sok olyan problémát találunk, melynek különböző, páronként kizáró, komplemens aspektusai vannak.

Atomi tapasztalásaink azt sugallják, hogy nem szabad azt mondanunk, hogy "ezek ellentmondó nézetek. Zavaró, hogy mindegyik igaznak tűnik, és rejtélyes, mikor azt találjuk, hogy az egyik nézőpont használata kizárja számunkra a másikat." Ehelyett inkább azt a görög örökségünket kellene hibáztatni, mely egy abszolút igen vagy nem "logikai" érvelésben való hitet hagyott ránk.

Doboz két kockával

A 2. ábra egy szemléltető modellt ábrázol, ami a komplementaritást hivatott illusztrálni, melyet valószínűleg Bohr javaslatára készítettek az 1939-es Világ Kiállításra. A balatoni szemináriumon bemutatott modell egy nagyméretű változat, amit H. M. Waage és J. A. Wheeler tervezett. Ha valaki szeretne egy másolatot készíteni, a teljes rajzot megtalálja a "The American Scientist, Vol. 44, No. 4, Oct. 1956., a J. A. Wheeler által írt "A Septet of Sybils" című cikkben. A berendezés néhány részletét a 3. ábra mutatja.***

Két nagy kartonkocka (A és B) vari a hosszú A B, mindkét végén átlátszó ablakú fiókban. A fiók egy két végén nyitott alagútban van úgy, hogy bármelyik oldalon kihúzhatjuk, hogy lássuk az ott levő kockát. Ahhoz, hogy az A kockát lássuk, a fiókot addig kell húzni, míg az A vége teljesen kijön: az A kocka látható, a B el van rejtve. Ahhoz, hogy a B kockát lássuk, át kell tolni a fiókot az alagúton egészen addig, amíg a B vég ki nem jön és B láthatóvá válik. Teljesen kihúzva vagy áttolva a fiókot, a dobozban egy átfordítószerkezet működésbe lép úgy, hogy ha az egyik kocka kijön és láthatóvá válik, akkor a másikat megdobja. (Ezt egy kalapács csinálja, ami megüti a kockák alatt levő gumipadlót.) A forgatószerkezet mindaddig nem működik, míg a fiók útjának legalább felét meg nem tette. Így aztán, ha a fiókot csak annyira nyomjuk be, hogy éppen benne legyen a dobozban, visszahúzhatjuk és újra megnézhetjük az A kockát, s ugyanazt az oldalát látjuk. De ha áttoljuk a fiókot egészen addig, míg B megjelenik, hallhatjuk, amint A bukfencezik, mielőtt B megjelenik; így aztán nem mondhatjuk meg előre, mit fog A mutatni, legközelebb megnézzük. Az egyik kocka megnézése megakadályoz bennünket abban, hogy tudjuk: mit fog a másik mutatni.

Ez tudományos értelemben nem "modell" ez csak egy játék, hogy illusztráljuk a komplementaritást. Ha az A véget az "ELEKTRON HELYE" (vagy "HOL?") néven nevezzük, a B vég lehet a "LEN DÜLE'T" (vagy "MILYEN GYORS?").

Sok más nézőpontpár van, melyek komplementerek - lényegesek, de páronként kizáróak; foglalkozva az egyikkel a másik kicsúszik a kezünkből.

Íme néhány J. A. Wheeler által az "A Septet of Sybils"-ben felsorolt válogatás.

AZ A VÉGÉN LEVŐ A KOCKA JELENTÉSE		A B VÉGÉN LEVŐ B KOCKA JELENTÉSE
Hely (pl. egy elektroné) vagy hol?		Lendület (elektroné) vagy milyen gyors?
KÍSÉRLET AZ ANYAG HULLÁMTERMÉSZETÉNEK MEGFIGYELÉSÉRE		KÍSÉRLET AZ ANYAG RÉSZECSKE'TERMÉSZE'TÉNEK MEGFIGYELÉSÉRE
Egy szó információátadásra való használata		Ugyanazon szó jelentésének analízise
Szabad akarat		Determizmus
Embertársaink szeretete		Igazságosság az emberiséggel szemben

A komplementaritás nem az ellentéteket állítja szembe, mint például a szeretet és a gyűlölet, hanem csak ugyanannak a dolognak kizáró vonatkozásait kapcsolja össze, mint a szeretet és az igazságosság. Meg kell tanulni együttélni a komplementaritással.

Bohr maga igen nagy fontosságot tulajdonított az utóbbi párnak.

Értve tanulás

A számítógépek segítségünkre lehetnek a természettudományok és természettudósok megértésének elsajátításában, vagy éppen fatális félreértésekhez vezetnek bennünket. Az értve tanulás, minden diáktól nagy erőfeszítést követel - úgymond meg kell rágnia az átnyújtott ételt és nemcsak arra használni a fogait, hogy feltépje az előemésztett anyagot borító celofánzacskót. A tudományt problémamegoldó - a megismerés problémája - folyamatra serkentőnek kell találnia. A számítógépek új problémákat vethetnek fel nekik, különböző modelleket sugallhatnak és gyakran még útmutatást is adnak. Ezekben a kérdések széles skáláját teszik fel, cselekvésre és gondolkodásra késztető kérdéseket. Bravó, ha azt meg tudják tenni.

De ha az általuk feltett kérdések csak arra valók, hogy előre gyártott azonnali válaszokat adjanak, hamarosan visszautasítjuk segítségüket.

Megemlítem még a tv által nyújtott természettudomány-tanításra vonatkozó visszautasító nemtetszésemet. Néhány megjegyzésre érdemes kivételtől eltekintve, a tv-gyártásvezetők (vagy forgatókönyvírók) nem tudnak ellenállni annak, hogy azonnali válaszokat adjanak. Ha csak kérdéseket tennének fel és hagynák a nézőt rágódni rajta, jó tanárok lehetnének; de rossz pszichológusok és azt hiszik, hogy egy gyors válasz amivel gondolkodást lehet megspórolni, a gondolkodó emberek tényleges fejlődéséhez vezet. Kíváncsi lennék, mit szólt volna ehhez Freud!

A sikeres válaszok önálló megtalálása kielégülést okoz, gyümölcsöző, hasonlatos ahhoz, mint amikor tudásunkat gyarapítjuk, amit mi megismerési folyamatnak nevezünk.

De amint Marx György figyelmeztetett az 1981-es Balaton-szemináriumon, "a siker gyakran a dogmatizmus szülőanyja". Ez az oka azután, hogy jobb hagyni a diákot megcsinálni személyes sikereit, semmint rátukmálni egy hivatalos "siker"-t, mely könnyen lehet, hogy hamarosan megváltozik.

A nevelés tervezésében egyre gyakrabban hallani egy figyelemre méltó kifejezést: "HANDS-ON" (cselekedj) - már a múzeumtervezők is használják. Igazán reményteljes hallani a "hands-on"-t, és most szeretnék javasolni egy további iránymutató kifejezést: "BRAINS-ON" (gondolkodj).

_______________