 x
x 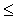 0, g'2
0, g'2  x
x 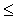 0,
... g'm
0,
... g'm  x
x 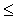 0
0Fizikai Szemle honlap |
Tartalomjegyzék |
Martinás Katalin
ELTE, Alacsony Hőmérséklet Fiz. Tanszék
1847. március 28-án született a Fejér megyei Sárosdon, régi, de már elszegényedett nemesi családból. Apja uradalmi intéző volt Pusztasárosdon. A család később Győrbe költözött. Farkas Gyula a középiskolai tanulmányait a győri bencés gimnáziumban végezte. Zongorázni tanult és zeneelméleti cikkei jelentek meg (szerepel a Zenei lexikonban).
1866-ban a pesti tudományegyetem jogi karára iratkozott be, de felvételizett a felsőbb zongoraiskolába is. A társait tehetségesebbnek találta magánál, ezért nem folytatta zongoratanulmányait, habár koncerteket továbbra is adott Tolnán, Székesfehérvárott és Nizzában is.
Apja tönkre ment, ezért megszakította tanulmányait. Házitanító lett. Élőszőr vidéken, majd Pesten. Jedlik Ányos hatására érdeklődése a fizika felé fordul, átiratkozik a természettan-vegytan szakra.
1870-74 a székesfehérvári reáltanoda tanára. Szaktárgyai mellett zeneoktatást is szervezett. Fizika könyvet írt a népiskolák számára. 74-ben hetilapot alapított Székesfehérvári Figyelő címmel. A lap kritikus szelleme miatt távozni kényszerült.
1874-80 házitanító gróf Batthány Geiza gyermekei mellett. A gróf fizika szertárat rendezett be, és a családdal utazhatott Olaszországba, Franciaországba. Ekkor került kapcsolatba Hermite, Villarceau és más matematikusokkal, akiknek hatására érdeklődése a matematika felé fordult.
1881-87 Batthány gróf támogatásával a matematikai kutatásaival foglalkozik. 1881 matematikából doktorált, majd magántanári képesítést nyer komplex függvénytanból. A pesti egyetem matematikát, függvénytant tanít.
1887 a kolozsvári egyetem elmélete fizikai tanszék vezetője lett. Hétszer volt az egyetem dékánja és egyszer a rektora. Az ő révén került Kolozsvárra Fejér Lipót, Riesz Frigyes és Haar Alfréd. Ortvay Gyula a kolozsvári egyetemen Tangl Károly tanársegéde volt a Kísérleti Fizika tanszéken, de nem szerette a kísérleteket. Farkas Gyulánál tartott elméleti kurzusokat, és Farkas Gyula nyugdíjaztatása után ő vette át a tanszék vezetését.
Közéleti tevékenysége: Az Erdélyi Múzeumegyletben a természettudományi szakosztály elnöke. Részt vett a “Mathematikai és Physikai Társulat" megalapításában. Padovában 1892-ben tartott Galilei ünnepségeken az egyetem küldötte. Díszdoktorrá avatták.
A Bolyai életmű népszerűsítésében is kiemelkedő érdemei vannak. Az xm = a + x egyenlet Bolyai Farkas által adott iterációs megoldását ő nevezte el Bolyai-algoritmusnak. Farkas Gyula mondta az ünnepi beszédet a Bolyai János szülőházán elhelyezett emléktábla avatásán, és ő képviselte az Akadémiát a Bolyai síremlék avatásán.
1898-ban az MTA levelező, majd 1914-ben rendes tagja.
1915-ben erősödő szembaja (glaucoma) miatt nyugdíjaztatta magát, arra hivatkozva, hogy az irodalmat már nem tudja naprakészen követni. Budapestre költözőn. 1930 december 27-én halt meg Pestszentlőrincen. A Zenei lexikon mellett az Új Magyar lexikon is megemlíti:
“F. Gy. matematikus és fizikus, egyetemi tanár. Elliptikus függvények elméletével, különböző algebrai problémákkal, iterációval foglalkozott. Legnagyobb eredményei a lineáris egyenlőtlenségekkel kapcsolatosak" A Farkas-tétel (mai megfogalmazásban): A
g'1 x
x 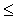 0, g'2
0, g'2  x
x 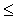 0,
... g'm
0,
... g'm  x
x 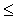 0
0
egyenlőtlenségeknek akkor és csak akkor következménye a g x 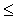 0 egyenlőtlenség, ha a g vektor a g1 g2 ... gm vektoroknak nem-negatív súlyokkal vett lineáris kombinációja. A tételt végtelen sok egyenlőtlenségre Haar Alfréd általánosította. Farkas és Haar eredményei nem keltettek különösebb feltűnést. A Farkas-tétel 1951 óta közismert, amikor Kuhn és Tucker munkája megjelent. A Kuhn-Tucker-tétel megadja annak szükséges és elégséges feltételét, hogy egy lehetséges megoldás optimalizálja a célfüggvényt. A bizonyítást a Farkas-tétel alapján végezték el.
0 egyenlőtlenség, ha a g vektor a g1 g2 ... gm vektoroknak nem-negatív súlyokkal vett lineáris kombinációja. A tételt végtelen sok egyenlőtlenségre Haar Alfréd általánosította. Farkas és Haar eredményei nem keltettek különösebb feltűnést. A Farkas-tétel 1951 óta közismert, amikor Kuhn és Tucker munkája megjelent. A Kuhn-Tucker-tétel megadja annak szükséges és elégséges feltételét, hogy egy lehetséges megoldás optimalizálja a célfüggvényt. A bizonyítást a Farkas-tétel alapján végezték el.
A Bolyai Társaság 1973-ban Farkas Gyula emlékdíjat alapított, amit évente osztanak ki.
Farkast tanárának tekintette Ortvay Rudolf, Gyulai Zoltán, Károly J. Irén, Kacsóh Pongrác. Előadás jegyzeteit mais élvezettel lehet forgatni. (Litografálva adta ki őket.)
Előadásai az egész elméleti fizikára kiterjednek. Fogalmazásuk rendkívül precíz és tömör. Nem jelentenek könnyű olvasmányt egy kezdő számára.
“A mechanika alaptanai" és az “Analytikus mechanika" című előadásaiban a tömegpont és merev rendszerek mechanikáját tárgyalja a Fourier-elv alapján. Az “Erőtan"-a potenciál elméletét és a stacionárius elektromos áramok tanát tartalmazza. “Az energia átalakulása" a termodinamikát, míg az “Energia terjedése" kontinuum-mechanikát igen általános feltevésekkel, a Fourier-féle elv kiegészítve a termodinamika fundamentális egyenlőtlenségével. Ez a kötet tárgyalja az elektrodinamikát és a relativitás elméletet is.
Amikor Farkas Gyula 1887-ben a kolozsvári egyetem matematikai fizikai tanszékének vezetője lett, a munkássága kizárólag matematikai volt, de ezeket azonnal abbahagyja, és fizikai problémákkal kezd foglalkozni. 1887-93 a fizikába való behatolás időszaka. Aktuális fizikai és kémiai problémákkal foglalkozik. A fenomenologikus irányzat következetes képviselője.
A legjelentékenyebb termodinamika dolgozata a Mathematikai és Physikai Lapokban 1895-ben magyarul és németül (Naturwissenschaftliche Berichte aus Ungarn) jelent meg, “A Carnot-Clausius-féle tétel egyszerűsített levezetése". A dolgozat célja a termodinamika II. főtételének olyan levezetését megadni, amely mentes a speciális feltételezésektől, például a körfolyamatoktól. Farkas a következő alaptételt állította fel:
“Adiabatikusan, azaz pusztán mechanikai műveletekkel egy test vagy testrendszer sem juttatható oly állapotba, amelybe puszta hőközléssel, azaz hőnek be- vagy kivezetése folytán a hőnek megváltoztatásával juthat."
Kimutatta, hogy ha ez nem teljesül, akkor ellentmondásba jutunk a Clausius-féle posztulátummal, amely szerint magasabb hőmérsékletű helyre alacsonyabb hőmérsékletű helyről nem megy át hő spontán folyamatban.
Felhívta a figyelmet arra, hogy a
Q=dE + Ada + Bdb + ...
elemi kőközlést meghatározó Pfaff-féle differenciál kifejezésnek nincs mindig integráló osztója. Megmutatta, hogy alaptétele teljesülése biztosítja az integráló osztó létezését.
Ez a dolgozat érdeklődést keltett. Voigl Woldemár az integráló osztó létezését magától értetődőnek vette, és Farkas Gyula cikke hatására keletkezett az integráló osztó létezésének vizsgálata. Maga Farkas Gyula így írt erről:
“Észrevehetően emelkedett itthon tudományos hitelem, midőn 1896-ban megjelent az akkor nagyhírű göttingeni professor Woldemár Voigt Mathematische Physik-jének második kötete."
Ortvay Rudolf Farkas Gyuláról szóló beszédében így írt erről:
“Bár a Caratheodory féle elv meglehetős feltűnést keltett és többen foglalkoztak vele, így T. Ehrenfest-Afanasjeva, Born, Lande, figyelmüket elkerülte Farkas Gyula 14 évvel előbb megjelent cikke, nyilván, mert a Naturwissenschaftliche Berichte aus Ungarn nem olyan közkézen forgó folyóirat és Farkas Gyula is elmulasztotta elméletére újólag felhívni a figyelmet, úgy hogy az itthon sem igen volt ismeretes és az előadó (Ortvay) figyelmét is Bródy Imre dr. hívta fel reá nemrég."
Magyarországi történetéről csak annyit, hogy tudomásom szerint egyedül Horváth József könyvében szerepel a Farkas-Caratheodory tétel. Fényes Imre méltatásáról sokan tudunk, de kevesen ismerik Farkas Gyula tényleges munkásságát.
Radnai Gyula a magyar fizika összefoglalójában Farkas-Caratheodory tételként említi. Jó lenne, ha ez hagyománnyá válna. Az eredeti dolgozatot élmény elolvasni, mindössze 5 oldal az egész. Nehéz eldönteni, hogy pozitív vagy negatív példának kell tekinteni. Lenyűgöző a tömörsége, precizitása. Valószínű viszont, hogy ez az eleganciája és a tömörsége okozta azt, hogy nem lett igazán ismert és népszerű.
Meg kell említeni, hogy ismerte Gibbs munkáit, így az akadémiai székfoglalójának témája az egyensúlyi állapot stabilitása volt. Ismerte és használta az entrópiaprodukció fogalmát. (Nem ezzel a névvel!) Megmutatta, hogy a kvázisztatikus közelítés valóban használható elvileg, mivel az entrópia növekedés a folyamat sebességében kvadratikus, így lassú folyamatokban tetszőlegesen kicsinnyé tehető.
Az 1892-es padovai látogatás döntően befolyásolja fizikai érdeklődését. A Galilei-emlékünnepségeken a mechanika általános egyensúlyi elvével, a virtuális munka elvével foglalkozik. A virtuális munka elvének gyökerei Galileiig nyúlnak vissza, de először Bernoulli mondta ki 1717-ben. Farkas Gyula a virtuális munka elvében találta meg a mechanika alaptörvényének legegyszerűbb és legáltalánosabb kifejezését, mégpedig nem az egyenlőséggel kifejezett szokásos alakjában, hanem az általánosabb, Fourier-től eredő egyenlőtlenséggel kifejezett formájában. (A virtuális munka nem lehet negatív). A Fourier-elvet Gauss 1829-ben újra felfedezi, de Farkas Gyuláé az érdem, hogy elődeinél sokkal általánosabban kimutatta használhatóságát a mozgás leírására. A virtuális elmozdulás fogalmát megszabadította a végtelen nagy sebesség feltételezésétől, így lehetővé vált a Fourier-elv beépítése a relativitáselméletbe. Nagyon szép ismertetést találhatunk erről Fényes Imre 1954-es cikkében.
Farkas Gyula első relativitáselméleti dolgozata 1906-ban született. Egyetemi előadásában (Energia terjedése) a Lorentz-féle transzformációt a következő feltételekből vezette le:
1. A transzformáció véges,
2. Az a téridő-sokaság konform leképezése
3. Van egy oly sebesség, mely minden téridő-rendszerben ugyanolyan nagyságú, helyföl, időtől, iránytól független.
Végezetül szeretném megköszönni Benedek András, Bródy András, Gábos Zoltán, Radnai Gyula és Ropolyi László segítségét. A munka OTKA támogatással készült.
Irodalom
________________________
Elhangzott az Eötvös Loránd Fizikai Társulat centenáriuma alkalmából tartott Magyarok a termodinamika történetében című ülésen, 1991. október 17-én.