FRAKTÁLOK A FIZIKÁBAN
II. Mintázatképződés növekedési jelenségekben

Vicsek Mária
MTA SZTAKI,
Vicsek Tamás
ELTE, Atomfizika Tanszék,
és MTA MFKI

Az egyensúlytól távoli jelenségek gyakran járnak két különböző állapotú tartomány, a kiinduláskor még egyszerű szerkezetű határfelületének mozgásával. Az így növekedő felületek általában megragadóan szép mintázatokat rajzolnak ki, amit néhány ábra segítségével illusztrálni is fogunk. A kialakuló mintázatok többnyire olyan bonyolult geometriai formák, amelyeket legjobban a fraktálgeometriával (lásd az I. részt, [1]) lehet leírni. A szerkezet nélküli, homogén anyagban tehát valamilyen önszervező mechanizmus hatására részletekben gazdag struktúra jöhet létre.

A fenti folyamatok a természetben és a különféle technológiákban egyaránt széles körben fordulnak elő [2]. A legtipikusabb példák között megemlíthetjük a hópelyhek keletkezését, a dielektromos kisülést (villámlást), az elektrokémiai leválasztást, a töréseket és a biológiai növekedést, amelyekre a továbbiakban majd részletesebben kitérünk. Az egyensúlytól távoli jelenségek, így a fraktálnövekedés iránt is az utóbbi években egyre intenzívebbé vált az érdeklődés, amit az ebből a témakörből rendezett konferenciák és friss publikációk nagy száma is jelez.

Az 1. ábra kristályosodás, viszkózus ujjasodás és elektrokémiai leválasztás során kialakuló mintázatokat mutat be. Jól látható, hogy bár nagyon különböző jelenségekről van szó, az alakzatok geometriájában mégis sok a közös vonás. Ugyanakkor, egyes oszlopokban a mintázatok egymástól markánsan különböző három fő típusa figyelhető meg. Ezek balról jobbra haladva: i) egyenletes sűrűségű, ii) klasszikus véletlen fraktál és iii) szimmetriával bíró alakzatok. A mintázatképződés vizsgálatakor azt a kérdéskört kívánják megválaszolni, hogy milyen feltételek mellett, hogyan és miért jön létre egy adott típusú fraktálalakzat a természetben.

A továbbiakban bemutatjuk a fraktálnövekedéssel kapcsolatos legfontosabb vizsgálati módszereket: a kísérleteket és a számítógépes szimulációt, valamint összefoglaljuk a segítségükkel kapott legérdekesebb eredményeket. (Az ismertetésre kerülő anyag jelentős része megtalálható [2]-ben, ezért külön hivatkozást elsősorban a [2]-ben nem tárgyalt esetekben fogunk megadni.)

Az elméleti módszerekkel és a számítógépes szimuláció segítségével kapott fraktálgeometriai eredmények felkeltették az érdeklődést olyan kísérleti rendszerek iránt, amelyekben fraktálmintázatok jönnek létre. Előkerültek olyan korábbi kísérleti eredmények, amelyeket az elméleti magyarázat hiányában eddig félretettek. Például a vékony filmrétegekben kialakuló véletlenszerűen elágazó struktúrákat évekkel ezelőtt már több laboratóriumban megfigyelték, de a fraktálgeometria elméleti kerete élesztette fel a velük kapcsolatos kísérleteket.

A mintázatképződés megértésére irányuló kísérletek előnye, hogy rendszerint viszonylag egyszerű körülményeket feltételeznek. A kialakuló formák általában szabad szemmel is láthatóak, a költségek is alacsonyabbak a szokásosnál. Vannak olyan kísérleti elrendezések, amelyek leegyszerűsített változatát az olvasó otthon is megvalósíthatja. Ilyen például a következőkben bemutatásra kerülő viszkózus ujjasodás vagy az elektrokémiai leválasztás.

2. ábra. Szimuláció és kísérlet során kialakuló hasonló mintázatok. a) Szimulációval előállított, 25 000 részecskét tartalmazó DLA klaszter 640 x 640-es rácson (a DLA modellt a szimulációkat tárgyaló részben ismertetjük részletesen). A klasztert körülvevő vonalak az azonos potenciálú (nyomású, hőmérsékletű, stb) helyeknek felelnek meg az adott alakra vonatkozóan. A potenciál a klaszteren zérus és egy 1100 rácsegységnyi átmérőjű körön egy. b) A szimulált DLA-ra hasonlító kísérleti mintázatot Hele-Shaw cella segítségével kapjuk. A 0,5 mm átmérőjű golyócskákat tartalmazó cellát vörös festékkel kevert glicerinnel töltöttük fel, majd levegőt fecskendeztünk bele. Az elágazó világos struktúra maga a buborék.

A kísérletek többségét abból a célból tervezték, hogy további elméleti vizsgálatokhoz szolgáltassanak adatot vagy felhasználásukkal különböző feltételezéseket igazoljanak. Erre a célra azok a legmegfelelőbb rendszerek, amelyekben a növekvő határfelület viselkedését viszonylag kis számú, jól megadható paraméter határozza meg. Lássunk néhány tipikus kísérletet, amely segítségével a mintázatképződés vizsgálható.

Ha egy viszkózus folyadékba belefecskendezünk egy kisebb viszkozitású másik folyadékot, ujjszerű alakzatok jönnek létre, ez az úgynevezett viszkózus ujjasodás. Ez a jelenség lép fel a másodlagos olajkinyerés során is. Olajfúráskor általában több lyukat fúrnak. Ha az egyes kutak körüli porózus kőzetekben levő olaj nagy része már a kúton keresztül eltávozott, a kutak közötti tartományból az alábbi módszerrel lehet további olajat kinyerni: vizet nyomunk be egy centrális helyzetben levő kútba, ekkor a víz a többi lyukhoz hajtja az olajat, ahonnan aztán az kitermelhető: Ennek hatékonyságát csökkenti, ha a víz nem egy gömbszerű fal alakjában terjed, hanem fraktálalakzatot képez, mivel ekkor az olaj nagy része a fraktál elágazásai között marad.

A kétdimenziós viszkózus ujjasodás jól bemutatható a Hele-Shaw-cella segítségével, amelyet korábban már ismertettünk [3]. Röviden: két üveglap között viszkózus folyadékot tartunk, és a felső üveglap közepébe fúrt lyukon keresztül egy kevésbé viszkózus folyadékot nyomunk be a cellába. A nyomás következtében behatoló folyadék nem a várt köralakban fog terjedni, hanem a felület instabilitása miatt elágazó határfelületet képez. Ebben az esetben az instabilitás azt jelenti, hogy a nyomáseloszlás hatására a felületnek azon részei, amelyek valamilyen véletlenszerű hatás következtében kicsit jobban kidudorodnak a környezetüknél, gyorsabban fognak nőni, mint a környezetükben levő részek. Emiatt még jobban kidudorodnak, még gyorsabban nőnek, és így tovább. Ez a jelenség egyszerre több helyen is lejátszódik a felület mentén; ez a bonyolult geometria eredete. Minél nagyobb a két folyadék viszkozitásának különbsége és a befecskendezés sebessége, valamint minél kisebb a két folyadék hátárán a felületi feszültség, annál gazdagabb mintázatot lehet kapni. A 2.b. ábra egy olyan cella felhasználásával készült, amelybe a két üveglap közé kis golyócskákat helyeztünk, hogy a porózus közeg hatását szemléltethessük.

A kísérlet egyszerű változata otthon is megvalósítható. Egy lapra kávéskanálnyi mézet teszünk, majd egy üveglapot úgy szorítunk a laphoz, hogy a méz vékony réteget képezve szétterüljön. Ezután megemeljük e felső üveglapot, és az oldalak felől behatoló levegő (ami itt a kevésbé viszkózus folyadék szerepét tölti be) fraktálmintázatot rajzol ki. Hasonlóan felületek ragasztásakor vagy átlátszó ragasztószalag feltépésekor is meg lehet figyelni viszkózus ujjakat:

Ha az üveglapokra rácsot karcolunk, anizotrópiát Vezetünk be a folyamatba. Háromszögrács esetén akár hópehely-szerű buborékot is kaphatunk (1.c. ábra).

Ismert, hogy a nemegyensúlyi megszilárdulási folyamatok gyakran vezetnek bonyolult geometriai mintázatok kialakulásához. Dendrites kristályok létrejöhetnek például egy tiszta, túlhűtött folyadékban. Ekkor a hőmérséklet eloszlásnak lesz döntő hatása a formák kialakulására, hasonlóan ahhoz, ahogy a viszkózus ujjasodás esetében a nyomáseloszlás határozta meg a határfelület mozgását (mindkét mennyiség helyfüggését a Laplace egyenlet írja le).

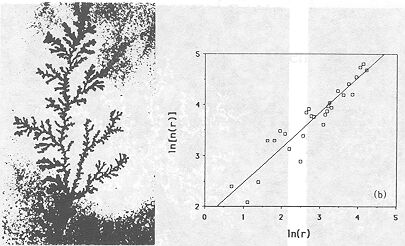
3. ábra. Amorf GeSe₂ vékonyrétegben növesztett, fához hasonlító kristály (balra). A jobboldali grafikon a kristálymintázat fraktáldimenziójára 1,69 körüli értéket ad.

A növekvő kristályos fázis rendezett mikroszkopikus szerkezete miatt egyetlen kristály kifejlődését alapvetően a felületi feszültség anizotrópiája befolyásolja. Ezt mutatja, hogy a kristályosodási kísérletekben megfigyelhető mintázatok közel szimmetrikusak. Ilyen szimmetrikus kristályok a hópelyhek is. Véletlen elágazású, szabálytalan fraktál kristályok is előállíthatók, például amorf vékonyrétegben végbemenő kristályosodási folyamattal.

A 3. ábra amorf GeSe₂ vékonyrétegben növesztett kristályt mutat. Ilyen ábrát akkor kapunk, ha a vákuumos párologtatással elkészített amorf mintát hővel kezeljük és az átkristályosodott (a képen fekete) tartományt tartalmazó részről transzmissziós elektronmikroszkóppal felvételt készítünk. A kristályosodás 220 °C-on megy végbe, amely tényegesen alacsonyabb, mint a GeSe₂ üveggé alakulási hőmérséklete.

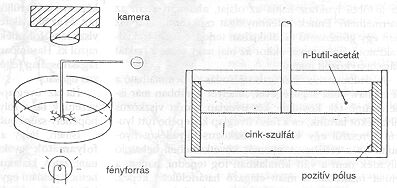
4.ábra. Kísérleti berendezés fémbokrok előállítására elektrokémiai leválasztással [4].

Ezen a példán mutatjuk be a kísérletek során kialakuló önhasonló mintázatok fraktáldimenziójának kiszámítására szolgáló módszerek lényegét. A kísérlet eredményeként kapott mintázatról fényképfelvételt készítünk. A kapott képet speciális eszközök (például scanner vagy videokamera + képprocesszor kártya) segítségével digitalizáljuk. Ez azt jelenti, hogy a folytonos képet a fény és sötétség különböző fokozatait érzékelve átalakítjuk a számítógép számára érthető 0 és 1 értékek sorozatára. Az alakzatra egy képzelt rácsot helyezünk, amelynek azon rácspontjaihoz rendelünk 1-t (sötét pontot), ahol a mintázathoz tartozó rész van. Összeszámoljuk a tömegközépponttól r távolságon belül elhelyezkedő sötét pontokat N(r)-t (ez esetünkben megfelel az objektum tömegének), és feltesszük, hogy N(r) ~ r^D. Ha a kitevő egy törtértéket ad, akkor objektumunk fraktál és dimenziója D. A kitevőt a következő eljárás segítségével határozzuk meg. Logaritmikus skálán ábrázoljuk a különböző r értékekhez tartozó N(r) értékeket, majd a pontokra egyenest illesztünk. Az illesztett egyenes meredeksége adja meg a fraktáldimenziót. A fent említett kristályosodási kísérlet feldolgozásakor ennek a módszernek egy változatát alkalmazták, N(r) helyett a dN(r)/dr= n(r) ~ r ^D-1 mennyiséget határoztuk meg, ahol n(r) dr a középponttól r, illetve r+ dr távolságra levő koncentrikus körök között található fekete pontok száma. Ezért a görbe meredeksége D - 1, amiből a kristály fraktáldimenziójára 1,69 körüli érték adódott.

A természetben gyakran találhatók fekete vagy barnásvöröses faalakú struktúrák mészkődarabok felületén. Ezeket a mintázatokat hívják ásványi dendriteknek, amelyeket a geológusok a következőképpen definiálnak: "réteglapokon és kőzetek elválási lapjain vasas és mangános oldatokból kivált fa illetve levél alakú bevonat". Ilyen dendritek láthatók a Fizikai Szemle februári számának címlapján. Ismert, hogy ezek kémiai kiválások (oxidok), amelyek a geológiai múltban akkor jöttek létre, mikor a mészkövet mangán és vas telített ionos oldata itatta át. A fraktálszerkezetű mangándendritek kialakulásának mechanizmusára több elképzelés született, de a probléma egyelőre nem tekinthető véglegesen megoldottnak.

Bonyolult mintázatok keletkeznek elektrokémiai leválasztás útján is. Az idevágó kísérletekben két elektródot mártanak bele valamilyen fémionokat tartalmazó elektrolit oldatba, és megfigyelik a katódon kiváló fématomokból álló szerkezetet. Az elektrokémiai leválasztáskor keletkező alakzatok sokfélesége a felhasznált feszültség és az oldat kémiai koncentrációjának függvénye. Bizonyos feltételek mellett a kiválasztódott fém fa vagy levél alakra emlékeztet (1.h. ábra).

5. ábra. Felület egy pontja körül lassan kialakuló repedéshálózat. A szerkezet fraktáldimenzióját 1,8 körüli értéknek találták.

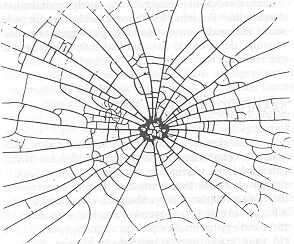
Ezt a fémlevelet egy egyszerű kísérlettel állíthatjuk elő [4]. Egy körülbelül 5 mm mély Petri-csészébe készítsünk cinkszulfát (körülbelül 2M koncentrációjú) oldatát és öntsünk rá n-butil-acetátot, hogy egy határfelület alakuljon ki. Tegyünk az edény közepére egy negatív elektródot; és vegyük körbe azt egy cinkből készült pozitív pólussal, ahogy azt a 4. ábra mutatja. 4,5 volt feszültségkülönbség hatására (tehát közönséges zsebtelep alkalmazásával) néhány perc alatt kialakul a fémlevél, amely egy tipikus fraktál 1,7 körüli dimenzióval.

Az 5. ábrán egy lassan kialakuló repedéshálózat látható, amely egy feszítő erőnek kitett felületen keletkezik. A kísérletben használt plexilap felületén a feszültséget egy, a szerző áltál egyelőre nem publikált vegyszer segítségével állították be. Adott helyre cseppentve a vegyszerből az atomok adszorpciója nagy feszültség-koncentrációt okoz a plexilap felületén. Az érintett terület szimmetriája miatt a repedésvonalak egy mag (a csepp helye) körül tömörülnek, onnan terjednek szét sugárirányban. Az 5. ábrát digitalizálva a kialakult mintázat fraktáldimenziójára 1,8 körüli érték adódott.

Az utóbbi két évben a biológiai mintázatok fraktál viselkedése iránt egyre nagyobb az érdeklődés. A fizikai és biológiai növekedési jelenségek során gyakran keletkeznek hasonló mintázatok. Ez a morfológiai egyezés izgalmas kérdéseket vet fel. Többek között: hogy létezik-e mélyebb kapcsolat az egyszerű fizikai folyamatok és az élővilágban megfigyelt alakzatok, formák között. Vajon melyik jelenségben (ha van egyáltalán ilyen) dominálhatnak a fizikai szempontok a genetikaiakhoz képest? A most ismertetésre kerülő eredmények nem adnak még választ ezekre a kérdésekre, de a jövendő kutatások számára kezdeti adatokat szolgáltatnak.

Fantasztikus szépségű struktúrák jönnek létre különböző baktériumok telepszerű növekedésekor. Például a néhány napra előlhagyott mindennapi ételeinkből is könnyen izolálható a Bacillus subtilis nevű baktérium. A kialakuló baktérium kolónia növekedését kísérleti körülmények között is megfigyelték (6. ábra). A táptalaj felszínét egy ponton megfertőzték. A tálkákat nedvesítő berendezésben tárolás után néhány napig egyenletes hőmérsékletű 35 ą 1 °C-on tartották. Ha a tápanyag koncentráció és nedvességtartalom megfelelő határok között volt, kialakultak az ábrán látható elágazó szerkezetek.

Különböző tesztekkel megpróbálták kideríteni, hogy ezekben a biológiai növekedési jelenségekben a morfológia kialakulásában ugyanaz a fizikai mechanizmus (a majd későbbiekben tárgyalt diffúzió limitált aggregáció: röviden DLA) játszik-e szerepet, amely egyes fizikai növekedési jelenségekben hasonló ágas-bogas struktúrát hoz létre. A tápanyag diffúzió, tehát fizikai mechanizmus útján terjed a táptalajban. Ezekben a kísérletekben az önhasonlóság okozója szintén a korábban említett instabilitás: a felület előrenyúló részein lévő baktériumok több tápanyaghoz jutnak, azt részben el is fogyasztják, így a lemaradó részek egyre lassabban fognak nőni. A tapasztalat azt mutatja, ha bizonyos határon túl növeljük a tápanyag koncentrációját, eltűnik az önhasonló fraktálszerkezet.

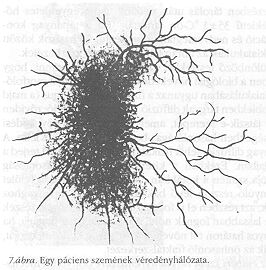
Az emberi szem véredényrendszere bonyolult mechanizmus útján fejlődik ki. A kialakuló, elágazó szerkezetű mintázat (7. ábra) nagyon hasonló a diffúzió limitált aggregációval létrejövőhöz. Az analógiát igazolja, hogy a retina véredényeire kiszámított 1,7 körüli fraktáldimenzió jól megegyezik a kétdimenzióban növesztett DLA fraktáldimenziójával. Jelenleg azt feltételezik, hogy a retina véredényrendszerének kialakulása során kapcsolat jön létre a véredények növekedése és a fényfelvevő idegvégződések kifejlődése között, amelyben diffúziós folyamatok fontos szerepet játszanak.

Sok további biológiai objektum, így a fák, az idegsejtekés a tüdő szerkezete is nagyon bonyolult és jól leírható a fraktálgeometria segítségével.

6. ábra. A kísérleti körülményektől függően bonyolult morfológiájú alakzatok jöhetnek létre Petri csészében táptalajon növesztett baktériumtelepből. A felső képen Bacillus substilis nevű baktériummal két helyen megfertőzött táptalajon kialakuló, két egymásfelé növekvő, bokorszerű struktúrát láthatunk. Ha a táptalaj tápanyag tartalma alacsonyabb és a nedvességet is alacsonyan tartjuk, akkor a baktérium telep alakja a diffúzió limitált aggregátuméhoz hasonló.

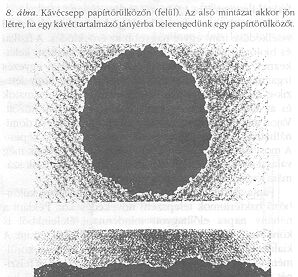
A természetben sok példát találunk önaffin felületek [1] kialakulására is, de a fraktálisan durva felületek növekedését az elmúlt évig kísérletileg kevésbé tanulmányozták. Közvetlen környezetünkben is gyakran előforduló jelenség, amikor egy nedvesítő folyadék porózus közegbe hatol be. Ez történik, amikor beázáskor a mennyezeten egy folt keletkezik, vagy a kiömlött kávét felitatjuk egy papírtörülközővel (8. ábra.) Ezek az úgynevezett kétfázisú viszkózus folyások porózus közegben.

A biológiai növekedés során nemcsak önhasonló szerkezetű baktériumtelepek keletkeznek. A körülményektől függően önaffin alakzatok is kialakulhatnak. Ezt igazolják az Escherichia coli és Bacillus subtilis baktériumokkal végzett kísérletek. Ha a tápanyag korlátlan mértékben, mindenhol rendelkezésre áll a növekedés teljes időtartama alatt, akkor a sejtek spontán szaporodásának véletlen sorozata játssza a főszerepet a telep felületének kialakulásában. Instabilitás hiányában ekkor a telep globálisan egyszerű szerkezetű, csak a pereme durva, mint a 8. ábrán látható kávéfolté.

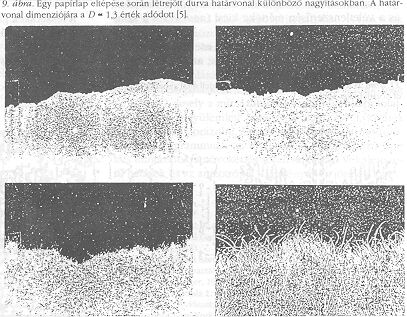
Érdekes, hogy egy olyan egyszerű folyamat, mint a papírlap eltépése, szintén fraktálgeometriához vezet [5]. Az ilyen irányú, gondosan kontrollált körülmények között végrehajtott kísérletek szerint ugyanis a tépés folyamata során kialakuló határvonal önaffin tulajdonságú (9. ábra.) A papírtépési kísérlet látszólag könnyű, de a szakítógépen levő műszer szerint egy közönséges lap párhuzamos befogás melletti széttépéséhez többnyire 100 kp-os súlynak megfelelő erőnél is nagyobbat kell alkalmazni, és a papír rendkívül összetett, rostos szerkezete miatt az eredmények interpretálása is érdekes kihívást jelentő elméleti feladat.

Számos további jelenség létezik, amelyben fraktálisan durva felület jön létre. Ide tartozik például az ülepedés során vastagodó anyag felszíne, egy kiégett tartomány kontúrja, de az erózió hatására kialakult sziklás hegységek vonulatai is.

A természettudományok terén az évszázadok során kialakult kutatási stratégiáknak megfelelően két fő vizsgálati módszert használtak: a különböző jelenségek lényegét elméletek konstruálása és kísérletek tervezése, illetve végrehajtása útján próbálták a kutatók megérteni. A legutóbbi évtizedben ezen két megközelítés mellé felzárkózott egy harmadik eljárás, a számítógépes szimuláció vagy másképpen számítógépes kísérlet. Ez az új módszer valahol a korábbi kettő között foglal helyet, mintegy ötvözi azokat. Egyfelől tisztán elméleti fogalmakkal (modell; egyenletek, stb.) operál, másfelől viszont lényege a vizsgálandó jelenség modelljének kísérletező vizsgálata. Tehát, egy szimuláció során a kutató oly módon változtatja a számítógépben szimulált modell paramétereit, és tanulmányozza a változó rendszer viselkedését, ahogy azt a valódi kísérletek során szokták a fizikusok. Így például lehet fokozatosan növelni (csökkenteni) a hőmérsékletnek, térfogatnak, nyomásnak, stb. megfelelő paraméterek értékét, és ki lehet számolni olyan mennyiségeket, amelyeket a kísérletekben általában mérnek.

A számítógépes szimuláció különösen alkalmas sok részecskét, sok részletet tartalmazó rendszerek kutatására, ahol sok alatt egy viszonylag nagy számot kell érteni. A számítógépben megvalósítható modellekben ez a szám általában több ezertől néhány millióig terjed. A nagyon bonyolult, szabálytalan alakzatok mennyiségi leírására csak az utóbbi években nyílt lehetőség, mikor a nagyteljesítményű számítógépek segítségével numerikus kísérleteket végezhettünk.

8. ábra. Kávécsepp papírtörülközőn (felül). Az alsó mintázat akkor jön létre, ha egy kávét tartalmazó tányérba beleengedünk egy papírtörülközőt.

A növekvő határfelületek által kirajzolt fraktálmintázatok képződése sikeresen szimulálható az úgynevezett aggregációs modellek segítségével [6]. Számos fontos fizikai, kémiai, biológiai és technológiai folyamat jellemző vonása az egyforma részecskék összetapadása, "aggregációja" útján létrejövő nagy halmazok (aggregátumok, klaszterek) kialakulása. Például a járművek kipufogó gázában található égéstermékek aggregáció útján egyesülnek a levegőben, majd megnövekedett súlyuk miatt leülepednek a talajra. A gyárkéményekből a légkörbe kerülő ipari szennyezés, valamint a nagyvárosaink utcáit borító por nagy része is aggregálódott füstrészecskékből áll. Sok ipari jelentőséggel is bíró anyag jön létre aggregációval, például a kolloidok, polimerek, kerámiák, üvegek és vékony filmrétegek.

Az aggregációs kutatások akkor gyorsultak fel igazán, amikor kiderült, hogy az aggregátumok többnyire nem közönséges kétdimenziós objektumok, hanem fraktálok. Witten és Sander amerikai fizikusok találtak ki egy egyszerű számítógépes modellt, a diffúzió által limitált (szabályozott) aggregációt, a DLA modellt, amely segítségével magyarázatot kaphatunk számos, a valóságban létező fraktáljellegű objektum kialakulására is.

A DLA modellben véletlen bolyongást végző részecskék hoznak létre egy növekvő klasztert. A kezdeti állapot egy góc, amelyet egy rács (például kétdimenzióban a négyzetrács) origójában helyezünk el. Ezt követően egy távoli pontból elindítunk egy másik részecskét, amely diffúziós mozgást végezve (véletlenül bolyongva) változtatja a helyét a rácson. Ha ennek a részecskének a pályája érinti az origóban levő részecskét, hozzáragad és megáll. Újabb részecskéket indítunk el egyesével, amelyek szintén megállnak és odatapadnak az előzőkhöz, ha hozzáérnek a növekvő klaszterhez. Ha a részecske nagyon távolra vetődik az origótól, egyszerűen eltávolítjuk és újat bocsátunk útjára. A növesztést addig folytatjuk, míg egy nagy aggregátumot kapunk. A növekedésben levő klaszter nyúlványai nagyobb valószínűséggel fognak be egy diffundáló részecskét, gyorsabban nőnek környezetüknél, azaz instabilak. Egyúttal mintegy "leárnyékolják" a mögöttük levő részeket (a bolyongó részecske csak igen kis valószínűséggel hatol be szűk fjordokba); ezért a keletkező aggregátum bokorszerű dendrites struktúrával rendelkező fraktál lesz (2.a. ábra.)

Ha az aggregáció síkon játszódik le, akkor a DLA klaszter fraktáldimenziója 1,7 körüli érték, míg háromdimenzióban 2,5.

A korábban ismertetett kísérletekben keletkező alakzatok többsége a DLA folyamat során kialakuló fraktálmintázatra emlékeztet, sőt, a kísérleti fraktáldimenziók is mind közel voltak 1,7-hez.

A struktúrából sok helyen kinövő ágak hierarchiája miatt nagyon egyenetlen az az eloszlás, amelyik egy részecske adott helyén való beépülésének valószínűségét adja meg. Az eloszlás értéke élesen megnő a hegyes csúcsoknál, de nagyon gyorsan zérushoz tart az ilyen klaszterekre jellemző mély öblök belső pontjaiban. Az I. részben bemutattunk egy ilyen multifraktál mértéket.

Könnyen belátható, hogy a véletlenül bolyongó részecske adott pontban és időben való előfordulásának p valószínűsége kielégíti a

= 0

Laplace-egyenletet. A részecske klaszterhez való tapadása mozgó peremfeltételnek felel meg. Másrészt tudjuk, hogy a természetben előforduló növekedési jelenségek többsége leírható a diffúziós egyenlet segítségével, amely a vizsgált fizikai folyamattól függően bizonyos közelítésekkel ekvivalens a valószínűségre, nyomásra, hőmérsékletre vagy az elektromos feszültségre felirt Laplace-egyenlettel. Így a DLA klaszterekkel analógiában levő példák között szerepel a viszkózus ujjasodás, a kristályosodás (hópelyhek), a dielektromos kisülés (villámlás) és az elektrokémiai leválasztás is.

9. ábra. Egy papírlap eltépése során létrejött durva határvonal különböző nagyításokban. A határvonal dimenziójára a D 1,3 érték adódott [5].

10. ábra. Felületi feszültség áltat dominált viszkózus ujjasodás számító gépes szimulációja során előállított mintázat. A csíkozás az időbeli fejlődés követését segíti.

A DLA modell számos változata ismert, amelyek különböző fizikai folyamatok megértéséhez nyújtanak segítséget. Ha például a modellbe bevisszük a felületi feszültségtől való függést, akkor sikerül a számítógépben az 1.d. ábrán bemutatottal analóg mintázatot előállítani (10. ábra.) Ez a felületi feszültség által dominált viszkózus ujjasodásra vonatkozó kísérleti eredményekkel megegyező tulajdonságokkal rendelkezik. Egy ilyen szimulációban jól követhető az ujjak kialakulásának valamim felhasadásának folyamata.

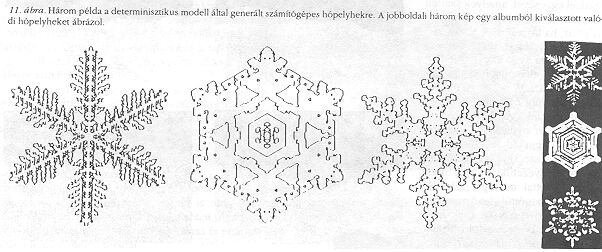
Rokon, de más faktorokat is figyelembe vevő modellekkel érthetővé válik a hópelyhek sokféleségének a rejtélye is. A 11. ábra jól szemlélteti, hogy a számítógépes szimuláció útján "előállított", és a valódi hópelyhek rendkívül hasonlóak. Ez az ábra úgy készült, hogy a szimuláció során a modell egyik paraméterét véletlenszerűen változtattuk, majd az így előállt alakzatok "párját" kikerestük egy könyvből, amelyben sokszáz valódi hópehely fényképe található. A hatszögszimmetriáért az alkalmazott háromszögrács a felelős. A rács alkalmazásával a jégkristályok felületi feszültségének anizotrópiáját (szögfüggését) szimuláltuk. Tehát akkor jönnek létre szabályos, szimmetrikus mintázatok, ha anizotrópia van jelen, és a véletlenszerűség mértéke kicsi (nem vezet a szimmetria lerombolásához).

Hangsúlyozni kell: minden fenti esetben a modellbe nem az adott geometria van beépítve, az egy önszervező mechanizmus hatására alakul ki a szimuláció során, hasonlóan ahhoz, ahogy ez a folyamat a természetben is lejátszódik.

Sok olyan fraktálokhoz vezető növekedési jelenség van, amelyik kevésbé összetett, mint az instabilitással bíró folyamatok. A perkolációs (szivárgási) modell képviseli talán a legegyszerűbb, önhasonló fraktálalakzatokhoz vezető növekedési folyamatot. Egy négyzetrács egyik rácspontjából (magból) kiindulva a vele szomszédos pontokat élőnek tekintjük abban az értelemben, hogy a jövőben elfoglalhatók lesznek. A következő lépésben ezeknek az élő helyeknek véletlenszerűen kiválasztott egyikét vagy adott p valószínűséggel betöltjük egy részecskével vagy 1-p valószínűséggel örökre megöljük . Ezt az eljárást ismételve egy nagy klasztert kapunk. Egy adott rácspont p valószínűséggel történő elfoglalását a következőképpen valósítjuk meg: generálunk egy r véletlen számot (egyenletes eloszlásút a (0,1) intervallumon) és betöltjük az adott helyet, ha r < p, A betöltött hely a növekvő klaszter része lesz, a vele szomszédos rácspontok élő helyek lesznek. Ha a betöltési valószínűséget (p-t) növeljük, akkor egy bizonyos p = p_c betöltési valószínűség felett, véges lesz annak a valószínűsége, hogy módszerünk egy minden határon túl növekedő klasztert eredményez. Itt p_c az úgynevezett perkolációs küszöb. A p < p_c betöltési valószínűség esetén létrejött véges klaszterek fraktálalakzatok.

Fenti folyamat számos terjedési jelenség modellezésére alkalmas, beleértve a járványokat, kémiai reakciókat, a tűz terjedését stb. Például a járványtan nyelvét használva: az élő helyek érzékenyek a fertőzésre, a megöltek immunisak, míg az elfoglalt rácspontok a megfertőzött személyeknek felelnek meg. Egy járvány az egész népességre ki fog terjedni, ha mindig van legalább egy "élő szomszéd".

11. ábra. Három példa a determinisztikus modell által generált számítógépes hópelyhekre. A jobboldali három kép egy albumból kiválasztott valódi hópelyheket ábrázol.

A részecskék pályája is meghatározó szerepet játszik a struktúra kialakulásában. A DLA modellben a részecskék diffúziós mozgást (véletlen bolyongást) végeznek. Ha a részecske egyenes vonal mentén mozog, akkor a folyamatot ballisztikus aggregációnak nevezzük, ez az eddigiektől nagyon eltérő alakzatokat hoz létre. A ballisztikus aggregáció segítségével jól modellezhető a vékony filmréteg növesztése gőzállapotból történő lecsapódáskor, mikor a gőz telítettsége olyan alacsony, hogy csak kevés ütközés fordulhat elő és így az atomok vagy molekulák egyenes vonal mentén mozognak. A kialakuló felületek önaffin fraktálok, mert az aggregátumok felszíne a klaszter növekedésével fokozatosan durvul.

A 12. ábrán látható bonyolult geometriai alakzat a következő egyszerű modell alkalmazásával állítható elő [6]. Képzeljük el, hogy egy egyenes szakasz mentén véletlenszerűen kiválasztott pontokból ragadós részecskéket ejtünk le, egyiket a másik után. Az aggregáció folyamata során a lefelé eső részecske vagy a közvetlenül alatta levő oszlopban található legfelső részecskéhez tapad, vagy a két szomszédos oszlop valamelyikéhez (a magasabbikhoz) oldalról. Végső pozícióját tehát az az oszlop határozza meg, amelyik a három közül a legmagasabb, mert lefelé haladtában először ehhez ér hozzá a részecske. Ez egy nagyon egyszerű algoritmus, és PC-ken is gyorsan látványos eredményekhez vezet.

A növekedési folyamat legelején a felület még viszonylag sima, hiszen a részecskék csak alig módosítják a kiindulási felületet, ami jelen esetben egy egyenes szakasz. Idővel a struktúra felülete egyre durvább lesz, és végül önaffin tulajdonsággal rendelkező fraktállá válik.

Vegyük észre, hogy a 12. ábrán látható szerkezet a növekedési szabály ellenére igen bonyolult, így például az üres tartományok mérete nagyon változatos. Összetettsége ellenére nagy hosszúságskálán a struktúra homogén és átlagos magassága, az időben (t) lineárisan nő, ahol az oszloponként lehelyezett részecskék száma. Megmutatható, hogy a felület vastagsága a szubsztrátum hossza (L) és a lehelyezés átlagos magasságának függvényében skálázódik (azaz a vastagság a hossz és az átlagos magasság hatványfüggvénye szerint változik), azaz

(t, L) ~

ahol a vastagság az egyes oszlopokhoz tartozó magasságok szórása (átlagos négyzetes eltérésük gyöke). Itt az és z = kitevők, amelyek a felületdurvulást írják le a növekedés során. Az f (x) konstans az x >> 1 értékekre, ezért aszimptotikusan a felület szerkezete olyan, hogy függőleges kiterjedése vízszintes méretének négyzetgyökével arányos. Ez a tulajdonság jó példa az önaffinitásra (lásd az I. részt), mert az egész felület minden részére érvényes lesz.

A fraktálokkal kapcsolatos izgalmas eredmények vázlatos ismertetésére tett kísérletünkkel talán sikerült érzékeltetnünk, hogy e bonyolult objektumok tanulmányozása még sok érdekes lehetőséget rejt magában. A fraktálok kutatása során közelebb juthatunk számos jelenség, folyamat megértéséhez illetve új jelenségek felfedezéséhez.

Írásunk elején felvetett kérdések teljesség igényével való megválaszolásától még távol vagyunk. Itt most részleges összefoglalásként egy sematikus ábrát adunk meg (13. ábra), amely a mintázatok képződésével kapcsolatban eddig felgyülemlett ismeretek egy részét kívánja szemléletesen ábrázolni. Ennek az úgynevezett morfológiai fázisdiagrammnak az értelmében a különböző tipikus mintázatok a növekedés során jelenlevő véletlenszerű hatások és az anizotrópia függvényében jönnek létre.

1. Vicsek M., Vicsek T., Fizikai Szemle, 43. 41. (1993)
2. T. Vicsek, Fractal Growth Phenomena (World scientific, singaporeNew York, 1992)
3. Vicsek T., Fizikai Szemle, 38. 249. (1988)
4. H. Takayasu, Fractals in the Physical sciences (Manchester Univ. Press, Manchester, 1990)
5. J. Kertész, Fractals 1. 68. (1993)
6. M. Vicsek, T. Vicsek, Fractal Growth (software) (World Scientific, Singapore-New York, 1991)