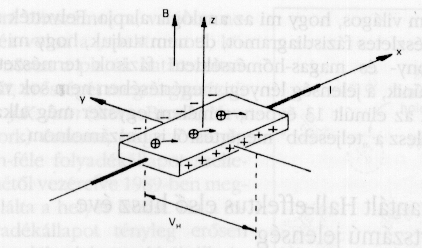
A Hall-effektus lényege: Ha I intenzitású pozitív x irányba folyó áramot B indukciójú, z irányú homogén mágneses térbe helyezünk, akkor e mágneses tér a pozitív töltéshordozókat negatív y irányba mozdítja el.
Fizikai Szemle honlap |
Tartalomjegyzék |
Ismét a kvantált Hall-effektusért!
Beleznay Ferenc
MTA MFA
Press Release 1998. október 13-áról:
A Királyi Svéd Tudományos Akadémia
az 1998-as Fizikai Nobel-díjat megosztva Robert B. Laughlinnak
(Stanford University, California, USA), Horst L. Störmernek
(Columbia University, New York és Bell Labs, New Jersey,
USA) és Daniel C. Tsuinak (Princeton University,
Princeton, New Jersey, USA) adományozta. A kutatók
a Nobel-díjat azért kapták, mert felfedezték,
hogy az egymással kölcsönható elektronok
nagy mágneses térben olyan új típusú
részecskéket formálnak, amelyek töltése
törtrésze az elektron töltésnek: "a
törttöltésű gerjesztésekkel rendelkező
új típusú kvantum folyadék felfedezéséért".
(Zárójelben: a felfedezés idején
mindhárman a Bell Laboratórium munkatársai
voltak!)
Bevezetés
Valamilyen értelemben a hír nem meglepő,
hiszen már 1985-ben, amikor Klaus von Klitzing a
Nobel-díjat az Egész számú kvantált
Hall-effektusért (IQHE) megkapta, ismert volt, hogy az
anomális, törtszámú jelenség
(Fractional QHE, FQHE) lényegesen különbözik
az egész számú jelenségtől,
ez utóbbi egyszerűen szólva a független
elektronok mozgási tulajdonsága, az előbbi
pedig az elektronok bonyolult kollektív mozgásának
a következménye. Amikor magáról a jelenségről
a Fizikai Szemle olvasóinak (1986., 94., 122. oldal) beszámoltunk
(Beleznay Ferenc: Egy félvezető rutinmérés
metamorfózisa I-II.), már tudtuk, hogy lényegesen
különböző eredetű jelenségekről
van szó, de a beszámoló második részében,
amely a törtszámú jelenséget ismertette,
talán több volt a kérdés, mint a határozott
megállapítás.

A Hall-effektus lényege: Ha
I intenzitású pozitív x irányba
folyó áramot B indukciójú,
z irányú homogén mágneses térbe
helyezünk, akkor e mágneses tér a pozitív
töltéshordozókat negatív y irányba
mozdítja el.
Nobel-díjat "ugyanannak a jelenségnek" ritkán adnak több alkalommal (a kondenzált rendszerek körében a kivételek éppen a kvantumfolyadékok esetében, a szupravezetés és szuperfolyékonyság területéről találhatóak), ezért talán érthető egyik más területen dolgozó fizikus barátom kérdése, hogy nem volt-e ez túlzás? Nekem erre a legmeggyőzőbb szubjektív válasz az, hogy a szintén Nobel-díjas, közismerten igen kritikus Philip Anderson, a kondenzált fizika talán legnagyobb élő alakja azt mondta: "It's so totally unlike states of matter that we had previously encountered". Azt hiszem, neki nyugodtan elhihetjük.
Szeretnénk azonban a Szemle olvasóival és a magyar fizikus társadalommal is megismertetni az elmúlt tízegynéhány év eredményeit, hogy bárki maga is meggyőződhessen erről, hiszen manapság amúgy sem túlságosan szerencsés csak "szaktekintélyek" véleményével érvelni.
A kvantált Hall-effektus első húsz éve - az egész számú jelenség
Fizikus számára néha a kísérleti
eredmények többet mondanak, mint egy hosszú
elbeszélés, ezért a kísérleti
technikák, a mérési eredmények fejlődésére
szabadjon az egész számú és a törtszámú
jelenség köréből is egy-egy mérést
megmutatni. Emlékezünk még a 1986-os cikkből
Klitzing mérésére, ezt mutatja az 1. ábra,
amelyen a kapuelektród előfeszítésének
a függvényében (ami a MOS szerkezet "kétdimenziós"
csatornájában az elektronok koncentrációját
változtatta) a szokásos longitudinális
ellenállással arányos feszültséget
és a tranzverzális, Hall-ellenállásra
(térre) jellemző Hall-feszültséget tüntettük
fel. Jól láthatóak a Hall-ellenállás
(koncentrációtól független) platói,
és az ezekkel együttjáró igen kis ellenállás
(disszipáció) értékek. (Emlékszünk
az első beszámolóból: a két
dimenziós világban a makroszkopikus, mérhető
Hall-ellenállás és az elmélet számára
fontos anyagi jellemző, a fajlagos - egységnyi felületre
vonatkoztatott - ellenállás megegyeznek egymással,
ezért az irodalomban legtöbbször ezeket a fajlagos
mennyiségeket mutatják. Így, eltekintve ettől
a történelmi jelentőségit ábrától,
a többi ábránkon, a későbbi méréseknél
megszokott módon, a 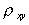 és
és
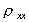 fajlagos
mennyiségek szerepelnek majd.)
fajlagos
mennyiségek szerepelnek majd.)
Egy mai, alkalmasan választott minta mérési eredményét mutatja a 2. ábra - elég alacsony hőmérsékleten a Hall-ellenállás szinte lépcsőszerű, és a lépcsőkön az értéke a mérési pontosság határain belül megegyezik az "elméleti" h/e2i értékkel. A mérési pontosság azt jelenti, hogy össze kellett hasonlítani a korábbi ellenállás-standardokkal. Hamar kiderült, hogy a leggondosabb mérés esetén is elkerülhetetlenül problémát okoz a standardok véges pontossága, és az is, hogy a különböző kvantum Hall-mintákon (Si MOS rendszer és GaAs-GaAIAs heteroszerkezet) mért értékek egymással 10-10 szinten megegyeznek. Ezért is 1990-ben elhatározták, hogy ettől kezdve az ellenállás egysége a kvantum Hall-mintákon mérhető h/e2 lesz, ennek számértékét az akkori mérések segítségével 25812,807 ohmnak rögzítették, és von Klitzing-állandónak nevezték el.
Ez persze nem csak kényelem és pontosság kérdése. Az egyik legfontosabb természeti állandó a Sommerfeld- féle finomszerkezeti állandó, amely lényegében az elektromágneses kölcsönhatás erősségét határozza meg, és a kvantumelektrodinamika (QED) legfontosabb próbája. Míg a hagyományos méréseknek (elektron anomális mágneses momentuma, hidrogén finomszerkezet, neutron de Broglie-hullámhossza...) a QED számolások pontossága körén belül meg kell egyezniök, a QHE mérés ezektől elvben független, így független próbája a QED-n alapuló fizikai rendszerünknek.
Ennek fontosságával, a jelenlegi mérések pontosságával és szinte természetfilozófiai jelentőségével foglalkozik Toichiro Kinoshita cikke ("The fine structure constant", Rep. Prog. Phys. 59, 1495-1492, 1996). Most elégedjünk meg azzal, hogy a legpontosabb QED mérések és a QHE mérések eredménye 10-8 szinten megegyeznek, és a különbség a mérési hibán belül van. Még az is metrológiai jellegű hír, hogy 1998 szeptemberében a két makroszkopikus kvantumjelenségen alapuló, és definíciószerűen rögzített adat, a QHE ellenállás egységének és a Josephson-effektuson alapuló feszültség-egység felhasználásával a Planck-állandót is pontosították, és arra készülnek, hogy ezek segítségével a tömeg egységét is kvantummérésekre vezessék vissza.
Azt hiszem, hogy Klitzing eredeti javaslata tökéletesen elfogadást nyert, és amit 1986-ban még csak érezni lehetett (hogyan is írtuk akkor? - "A mérésügyi hivatalok komolyan foglalkoznak azzal a lehetőséggel, hogy a QHE-val mért ellenállás dimenziójú h/e2 értéket fogadják el az ellenállás egység alapjául"), az ma maradék nélkül valóra vált. Fontos-e ez egyáltalán? 1894-ben Michelson aggódott a fizika intellektuális haláláért, mert úgy érezte, hogy csak a mérések pontosítása van hátra. Tudjuk, hogy ez nem így volt, és hisszük, hogy a kvantitatív eredmények mögött most is a jövő fizikája lehet!
Kicsit ünneprontó mondatokkal kell ezt a részt zárnunk. Ha már a mérésügyi hivatalok ezt használják, ha már a kvantum Hall-mérések (még Magyarországon is!) bevonultak az egyetemi labormérések körébe, mit lehet még ezen kutatni? Nos mind a mai napig nincs a QHE-nek olyan prediktív elmélete, amely a kísérletek eredményeit részleteiben megjósolná, mi több, számtalan olyan kísérlet van, amelyek magyarázata nem is megy a hagyományos lokalizáción alapuló elmélettel. A legalacsonyabb spinpolarizált nívón olyan összetett spingerjesztéseket találtak (skirmionok), amelyek korábban csak elméletben léteztek. A letörés legújabb méréseivel nagyfokú analógiát találtak a szupravezetőkkel - csak éppen az nem világos, hogy mi az analógia alapja. Felvették az első részletes fázisdiagramot, de nem tudjuk, hogy mi az alacsony- és magas-hőmérsékletű fázisok természete. Úgy tűnik, a jelenség lényegi megértésében nem sok változott az elmúlt 13 évben, remélem egyszer még alkalmam lesz a "teljesebb" megértésről is beszámolnom.
A kvantált Hall-effektus első húsz éve - törtszámú jelenség
Kezdjük ismét a kísérletekkel. A ma már Nobel-díjas kísérletben Tsui és Störmer a mágnestér függvényében (ami egyenértékű a Landau-pályák betöltöttségének a változtatásával), mérték a Hall-ellenállást, és azt találták, hogy plató jelenik meg meghatározott (1/3, 2/3) betöltöttségeknél is (3. ábra). Az akkori mérés "célját és történetét" már 1986-ban leírtuk, most talán csak annyit, hogy a heteroszerkezetet előállító, most már Kaliforniában dolgozó társszerző (Gossard) nem kapott díjat, hiszen azt legfeljebb 3 kutató között osztják! (Egy kis érdekesség, hogy a díj kapcsán sokat szereplő Störmer a Lucent Technology nevű óriásvállalat jóvoltából - ez a vállalat, amely az AT&T-ből kivált és jelenleg a Bell Lab gazdája - Magyarországon is telekonferenciát tartott, és itt említette meg, hogy legújabb munkájukban az eredetileg megtalálni vélt Wigner-kristályt látták!)
A harmadik díjazott, Laughlin egy éven belül megmagyarázta a jelenséget, - ahogy erről is beszámoltunk, az a szép, hogy bár sok új eredmény született, az eredeti magyarázat ma is a jelenség megértésének az alapja.
Hogy néznek ki ma a kísérletek? A
4. ábra
mutat egy korszerű mérést (ennek szintén
társszerzői Störmer és Tsui, akik az
elmúlt évtizedben - bár Tsui a Princetoni
egyetemre ment - változatlanul együtt dolgoztak),
ezen látható, hogy több-kevesebb "kifejlettséggel"
eléggé rapszodikusan több, különféle
törtszámú plató lép fel. Neugebauer
tanár úr még az ötvenes évek
végén bevezető előadást tartott
az atomfizikába, és ott mesélte el, hogy
a Balmer-formulában az volt a szenzációs,
hogy sokkal nehezebb egy mérési hibák miatt
esetleg nem teljes diszkrét számsorra törvényt
találni, mint egy folytonos függvényt megsejteni
és illeszteni. Ha így első blikkre ránézünk
az itteni törtszámokra, valóban nehéz
volna a "spektrumot", különösen a platók
határozottságát, erősségét
megmagyarázni.
J. K. Jain (Stony Brook, New York) érdeme, hogy
a Laughlin-féle folyadékállapot szellemétől
vezérelve 1989-ben megtalálta a helyes leírást.
Ha a folyadékállapot tényleg erősen
korrelált elektronokból áll átlagosan
feltehetjük, hogy az elektronok egyenletesen töltik
ki a síkot (emlékezünk: minden kvantum Hall-rendszer
kétdimenziós!). De így egy-egy elektron,
a betöltöttségtől függően,
átlagosan a mágneses tér elemi fluxuskvantumaival
együtt mozog. (Ahogy az impulzusmomentumnak is van elemi
egysége, a 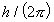 Planck-állandó, úgy
a mágneses fluxus legkisebb egysége a
Planck-állandó, úgy
a mágneses fluxus legkisebb egysége a
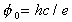 elemi kvantum-mechanikai fluxus érték. A fluxuskvantumok
sűrűsége a mágneses teret határozza
meg, az elektronok sűrűségének és
a fluxuskvantumok sűrűségének hányadosa
éppen a Landau-nívók betöltöttségével
egyezik meg.) Ahelyett tehát, hogy az elektronokat a teljes
külső mágneses térben mozgó részecskéknek
tekintjük, kapcsoljunk hozzájuk a mágneses
tér egy részét, és vizsgáljuk
a mozgást a maradék mágneses térben.
Jain minden elektronhoz két fluxuskvantumot csatolt (ez
feles betöltésnek felel meg), ez az összetett
képződmény a "kompozit fermion".
Ezt formálisan ennek a kiválasztott, elektronhoz
csatolt fiktív térnek, a térelméletben
ismert Chern-Simons-mértéktér segítségével
tehetjük meg. Az eredmény az lesz, hogy az elektronok
kölcsönhatását ez a tér átlagosan
kiegyenlíti, tehát a maradék térben
az így bevezetett összetett, kompozit részecskék
már mint kölcsönhatás-mentes részek
mozognak. Ezek a kompozit fermionok a (maradék) mágneses
térben Landau-pályákat alkotnak, és
az ezekkel létrejövő "egész számú
QHE" felel meg az eredeti rendszer "törtszámú"
viselkedésének. Ez a mélyebb magyarázata
annak, amit már az 1986-os ismertetőben hangsúlyoztunk,
hogy bár a jelenségek eredete teljesen különböző,
a kísérletek mégis nagyfokú hasonlóságot
mutatnak.
elemi kvantum-mechanikai fluxus érték. A fluxuskvantumok
sűrűsége a mágneses teret határozza
meg, az elektronok sűrűségének és
a fluxuskvantumok sűrűségének hányadosa
éppen a Landau-nívók betöltöttségével
egyezik meg.) Ahelyett tehát, hogy az elektronokat a teljes
külső mágneses térben mozgó részecskéknek
tekintjük, kapcsoljunk hozzájuk a mágneses
tér egy részét, és vizsgáljuk
a mozgást a maradék mágneses térben.
Jain minden elektronhoz két fluxuskvantumot csatolt (ez
feles betöltésnek felel meg), ez az összetett
képződmény a "kompozit fermion".
Ezt formálisan ennek a kiválasztott, elektronhoz
csatolt fiktív térnek, a térelméletben
ismert Chern-Simons-mértéktér segítségével
tehetjük meg. Az eredmény az lesz, hogy az elektronok
kölcsönhatását ez a tér átlagosan
kiegyenlíti, tehát a maradék térben
az így bevezetett összetett, kompozit részecskék
már mint kölcsönhatás-mentes részek
mozognak. Ezek a kompozit fermionok a (maradék) mágneses
térben Landau-pályákat alkotnak, és
az ezekkel létrejövő "egész számú
QHE" felel meg az eredeti rendszer "törtszámú"
viselkedésének. Ez a mélyebb magyarázata
annak, amit már az 1986-os ismertetőben hangsúlyoztunk,
hogy bár a jelenségek eredete teljesen különböző,
a kísérletek mégis nagyfokú hasonlóságot
mutatnak.
Jain elméletének szép sikere, hogy a sajátos törtszámú spektruűmra egyszerű magyarázatot szolgáltat, a lehetséges törtszámok p/(2mp + 1) alakúak, ahol m kis pozitív egész és p kis előjeles egész szám. (m = 1 esetén hasonlítsuk össze az elméleti betöltöttségeket az ábra "jobb oldalán", az 1/2 betöltöttségek körül talált kísérleti értékekkel!)
Laughlin elméletében fontos volt, hogy a tört
nevezője nem lehet páros szám, Jain formulájából
is ugyanez jön ki. Mégis a mérték-térnél
(és a levezetésben) fontos szerepe van az 1/2-es
betöltésnek. Hatalmas kísérleti anyag
és elméleti megfontolás mutatja, hogy ez
valóban így van elsősorban a Bell Laboratórium
munkatársai -, a kompozit fermionnak számos kísérleti
bizonyítékát találták. Talán
a legszebb, hogy a minta felületén haladó akusztikus
felületi hullám (SAW) elektromos gödrébe
zárva a kompozit fermion dinamikus tulajdonságai
(például annak meglepően nagy effektív
tömege) közvetlenül is meghatározhatók
- ez a mérés is ugyanott történt R.
L. Willett vezetésével.
A Nobel-közlemény külön hangsúlyozza a tört-töltésű gerjesztések jelentőségét. Már a korábbi ismertetőben is említettük, hogy a Laughlin elméletből tört-töltésű gerjesztések következnek. Ezt teszi most jobban érthetővé a kompozit kép bevezetése. Képzeljük el, hogy az 1/3-os betöltöttségnél egy-egy elektron 3 fluxuskvantummal van összecsatolva. Ha a mágneses teret kicsit megnöveljük, akkor az elektronokra több fluxuskvantum jut - a Laughlin-állapot azonban olyan, hogy a folyadékállapot megváltozása csak energia befektetéssel lehetséges, ez a kvantum-folyadék összenyomhatatlan. Ezért képzeljük el, hogy a folyadékban kis "lyuk" keletkezik, amelyben van egy fluxuskvantum, de nincsen benne elektron! Így a homogén (negatív) töltésű folyadékban egy "töltetlen" lyuk keletkezik. A félvezetők sávelméletéből tudjuk, hogy ez épp úgy fog viselkedni, mint egy megfelelő pozitív töltésű effektív részecske. (Hogyan is képzelhetjük ezt el? A vízben a nehézségi erő a folyadékot lefelé "húzza", a buborékot azonban ugyanaz felfelé hajtja; ellenkező a "töltése".) Mekkora ennek a töltése? Pont annyi, mint amennyi a folyadékban 1 fluxuskvantumhoz tartoznék, jelen esetben 1/3! Hogy az egész jobban érthető legyen, az 5. ábrán ennek sematikus képét le is rajzoltuk.
Tört töltést már sokszor vezettek be elméleti fizikusok, létét nem is tagadjuk, sajnos eddig még soha sem láttuk kísérletekben. A legutolsó években megtörtént az áttörés, két különféle kísérletben is megmutatták ezek hatását. V. J. Goldman és munkatársai parányi kis szigetet (kvantum antidotot) alakítottak ki a kvantum Hall-rendszerben és megmérték egy igen érzékeny elektrométerrel, hogyan változik annak töltése az alkalmazott kapu-feszültséggel. Ezt a mérést látjuk a 6. ábrán két különböző (1 és 1/3) betöltöttség esetén. Erre a mérésre is hivatkozik a Nobel-bizottság bejelentéséhez csatolt magyarázat.
A másik típusú mérések elvégzői, két független csoport (Franciaországból és Izraelből) úgy vélik, hogy ez a mérés csak átlagosan mutatja a gerjesztések töltését, így annak értéke még fluktuálhat (emlékezünk, Milliken szintén Nobel-díjas mérése az elektronok egyedi töltéseit és azok univerzális állandó értékét határozta meg). Ők a folyadékhoz illesztett parányi kontaktusok (valójában alagútdiódák) áramának zaját mérték, ez a zaj függ az áramot szállító effektív részecskék töltésétől, és pont megegyezik a várt töltés értékkel.
Mi jön (jöhet) még?
Amint már korábban említettük, a jelenségnek még nagy effektív tömege) közvetlenül is meghatározhatók - nincsen átfogó, részleteket megmagyarázó elmélete. Talán ez isjellemző korunkra, hogy rögtön a QHE felfedezésekor mikroszkopikus elméletet akartunk találni, és fenomenologikus szinten még nem sokat tisztáztunk. Valahogyan olyan a helyzet, mintha a szupravezetés BCS-elméletét előbb akarták volna megcsinálni, minthogy a kétfolyadék-elmélet és a Landau-elmélet megszületett volna. Ma már tudjuk, hogy a jelenségek leírására ezek a fenomenologikus elméletek alkalmasak, a mikroszkopikus elmélet ezek "levezetésére", megmagyarázására szolgál. Ennek jelentőségét és történetét ismerve nem csodálhatjuk, hogy a QHE esetében sok kis részletes számolás mellett a lényeget talán még ma sem ismerjük. Furcsa módon a törtszámú jelenség, annak térelméleti megalapozása miatt, mintha ma közelebb állna a teljes megértéshez. Bár itt is nyitott még az összetett rendszerek statisztikus viselkedésének a kérdése, és elképzelhető, hogy legalábbis bizonyos körülmények között a szokásos "fermifolyadék"-szerű leírás sem alkalmazható. Minden esetre jó hír, hogy van még mit csinálni ezen a területen.
Bár ez is szép befejezés lehetne, jó lenne még valamit hangsúlyozni, ami a szerző magánvéleménye, és nem kell mindenkinek elfogadnia. A QHE nem csak a két Nobel-díj miatt, de a megszámlálhatatlan szép kísérleti és invenciózus elméleti munka miatt is kétségen kívül a mai szilárdtestfizika egyik legizgalmasabb területe. A Nobel-díj bejelentése során a legkülönfélébb források kiemelték, hogy ez a díj a kvantumfizika újabb diadala. Szeretném hozzátenni, hogy nem csak a kvantummechanika, hanem a félvezető fizika diadala is, és jó példája, hogy a parányi félvezető szerkezetek olyan csodálatos laboratóriumot szolgálnak, amelyben szinte mindent megtehetünk, amit csak elképzelünk. (Störmer a már említett interjúban hangsúlyozta, hogy ő nem mérnök, nem is ért a mérnöki munkához, de felfedezésük nem lett volna lehetséges a hihetetlen szintre fejlődött félvezető-technika nélkül. Ezért is, minden álszerénység nélkül azt mondta, hogy a felfedezés sok ember munkájának gyümölcse, és szerencsésnek érzi magát, hogy éppen a megfelelő helyen és időben ebben ő is részt vett.)
Ezért érzem tragédiának, hogy a magyarországi
egyetemeken a félvezetők kutatása és
oktatása, véleményem szerint, igen fejletlen.
Nem csak magunkat, de a jövő kutatóit is kirekesztjük
a holnap (és a ma!) szilárdtestfizikájából,
ha egy ilyen fontos területen nem teszünk meg mindent,
hogy felzárkózzunk - nem is említve annak
következményeit, ha nem leszünk képesek
a csúcstechnikai ipart itthon is fejleszteni!