
Benedictine monastery and school in 1684 (Pannonhalma)
Fizikai Szemle honlap |
Tartalomjegyzék |
Katalin Papp
Department of Experimental Physics
József Attila University, Szeged
"The future will be, like schools are today"
Albert Szent-Györgyi
Nobel laureate 1937, Szeged, Hungary
The Past: excellent teachers - famous students
When Adalbert the Saint was on his way from Prague to Rome, at the request of Géza, chief of Hungarians, Adalbert stopped on Hungarian soil and founded the first Benedictine monastery and school in 996, more than thousand years ago (Pannonhalma). Starting from this point the thousand-year long development of Hungarian schools has been uninterrupted, leading to the Benedictine monk professor Ányos István Jedlik (1800-1895), who became the first physicist among the members of the Hungarian Academy. He was teaching first at the Győr secondary school of his Order, later became professor of physics/mechanics of the Pest University. He constructed the dynamo before Siemens and built a machine to make diffraction gratings. Throughout the troubled centuries of Hungary, the autonomy of schools and the quality of teacher training at universities has always played a decisive role in preserving the cultural heritage of the nation [1].

Benedictine monastery and school in 1684 (Pannonhalma)
In earlier centuries the churches raised Hungarian schools to a high level. Besides the Benedictines, the Roman Catholic School of the Piarist Order in Budapest deserves mentioning, where Roland Eötvös, furthermore the Nobel laureate chemists George de Hevesy (N.L. 1943) and George Olah (N.L. 1994) studied, among others. The quality of the Piacist School was due to their legendary teachers. József Öveges (1895-1979), the teacher of George Olah, introduced nuclear experimentation with scintillator detector and Geiger tube for students already in the early 1940s. His simple but shocking experiments presented on television made him a favorite of the whole nation. He received the Prometheus Prize of the Eötvös Society for spreading scientific thinking among people. Another teacher of this school, Mihály Kovács built computers with his students in the 1960s, making him to one of the first propagators of the computer era in Hungary. The personal computers were distributed to each Hungarian secondary school free of charge in 1983. Since then thousands of students leave secondary school year by year with BASIC programming knowledge. Geiger counters for scanning radioactivity in the environment have become everyday school equipment.
Calvinist schools as well have four to five century-old traditions; Zoltan Bay attended the Calvinist School in Debrecen, Albert Szent-Györgyi (N.L. 1937) did in Budapest. But most legendary is the "Fasori" Lutheran Gymnasium in Budapest, its fame having been propagated by its Nobel laureates, Eugene P. Wigner (N.L. 1963) and John C. Harsanyi (N.L. 1994), furthermore John von Neumann. Theodore Herzl, the founder of the movement for an independent Jewish state, also graduated from this school. (Herzl attended the Eötvös Realgymnasium in downtown Pest, but graduated from the "Fasori" Gymnasium.)
Eugene P. Wigner quoted the merits of the legendary teachers of the Lutheran Gymnasium: László Rátz in mathematics and Sándor Mikola in physics. One cannot find a Neumann Street or Wigner Street in Budapest, but there is a Rátz László Street. Today, the János Bolyai Mathematical Society distributes the Rátz Prize for the best mathematics teachers, the Roland Eötvös Physical Society gives the Mikola Prize for the best physics teachers of the country every year. These prizes - decided by the teachers' nation-wide community - have a respect higher than any official acknowledgement. Sándor Mikola was elected a member of the Hungarian Academy of Sciences for his research in materials science. Later on, further teachers of the Lutheran Gymnasium excelled: János Renner (the teacher of John C. Harsanyi) was student of Roland Eötvös; he improved Eötvös' experiments on the proportionality of mass and gravity and received the first Eötvös Medal of the Eötvös Society. Another teacher, Miklós Vermes conducted research on electronics already in the 1940s; Vermes Medal is awarded now for special excellence in experimental education.
At the arrival of the industrial revolution, József Eötvös, the minister of culture decided to introduce secular schools with an enlightened spirit. He asked Mór Kármán to do the job, who then created a Model: the "Minta" Gymnasium in Budapest, made famous by its students like Theodore von Kármán, Nicholas Kurti, Edward Teller (in physics) Michael Polanyi (in chemistry), Thomas Balogh, Nicholas Kaldor (in economics), and Peter Lax (in mathematics). The pedagogical achievement of Mór Kármán were not left unnoticed; he was ennobled by the emperor-king Franz Josef in 1889. (To excel as school teacher is not an everyday way of becoming a nobleman.)
School report of Andrew Grove in his age 18, at Madách Imre Gymnasium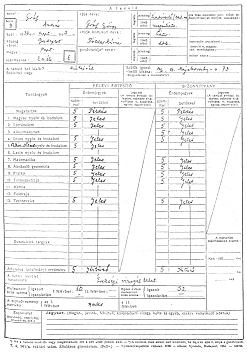
There are other secular schools without any privilege, excelling trough the efforts of their teachers. The Berzsenyi Gymnasium gave the world a long sequence of winners at student Olympiads, furthermore Marcel Grossmann, John G. Kemeny, George Klein, George Soros, in addition to politicians like Count Mihály Károlyi (president of the democratic republic in 1919) and Tom Lantos. (He was born in Budapest 1928, went to the U.S. with university scholarship in 1947. He is now member of the U.S. Congress, representing California; was consular of the U.S. Senate in economic and foreign affairs 1966-1980, now member of the Congress' Foreign Policy Commission. He speaks Hungarian and visits his native country frequently.)
Leo Szilard and Arthur Koestler studied in the Kemény Zsigmond Realgymnasium.
One of the characteristics of these schools and their physics teachers was that they were open to the stormy development of science. Virgil Klatt (teacher of Philip von Lenard N.L. 1905), Sándor Mikola (teacher of Neumann and Wigner), Miklós Vermes (from the Lutheran Gymnasium). Karl F. Novobátzky (regular speaker at Ortvay Colloquium), recently Esther Tóth (past secretary of the Group for International Research in the Education of Physic) published research papers in prominent physics journals. Ireneus Károly (teacher at the Premonstratensian Gymnasium in Nagyvárad) demonstrated the wireless telegraph through a distance of 10 km in the same year that Marconi invented the radio (1895); he established an X-ray laboratory within a year after Röntgen's discovery (1896). On 15 February 1896 pupils demonstrated X-rays with their own equipment in the Catholic Gymnasium of Kolozsvár/Cluj-Napoca, three months after the discovery. József Öveges wrote a book for teenagers on ionizing radiation, Miklós Vermes on relativity, Mihály Kovács on computere already around 1960. The schoolbooks of Ester Tóth about modern physics have been published even in China and Japan. She was invited to the Lawrence Livermore Radiation Laboratory (California) to report on her country wide radon survey, organized via the network of school teachers and their pupils, and performed in the bedrooms of over ten thousand pupils in Hungarian villages. Hungarian gymnasiums measured the Chernobyl fallout in 1986. Hungarian physics teachers visited Three Mile Island and Chernobyl power plants (to obtain first hand information by performing their own measurements after the nuclear accidents). When Hungary became a member, physics teachers and competition-winning gymnasium students visited the laboratories of CERN. High temperature superconductivity was demonstrated nation-wide a few months after the discovery; thus students could explain the experienced phenomenon to their parents when the Nobel Prize for it was announced. Doctor degrees are not uncommon among Hungarian teachers. Since John von Neumann to our limes it occurred that gymnasium students publish research papers in international physics journals.
The certificate of Leo Szilard at Kemény Zsigmond Realgymnasium
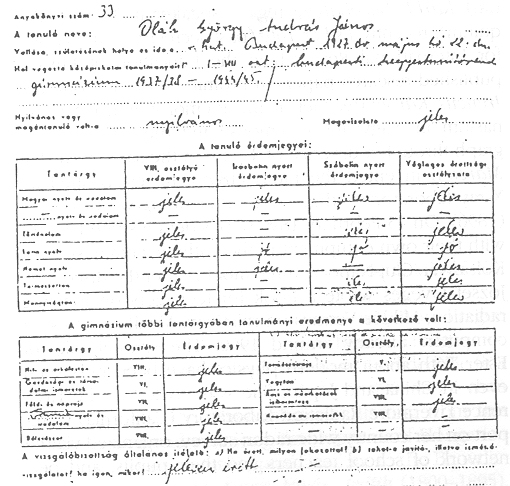
School report of George Olah at Gymnasium of Piarist Order
Professor Roland Eötvös organized the first in-service-teacher-training seminar in 1905 [2]. The physics teachers meetings have operated for hundred years, attended by hundreds of school teachers every year. The program of the meetings is decided by the teachers themselves, selecting the speakers from among prominent professors and the best school teachers. Professor Rudolf Ortvay organized teacher training on quantum mechanics already in 1930, distributing them even his booklet on the subject.
About one hundred years ago a mathematics teacher Dániel Arany, got the idea to create a problem solving Journal for secondary school students (1894). This student Journal was second only to Vuibert`s Journal de mathématiques élémentaires (1876). The Középiskolai Matematikai és Fizikai Lapok (KöMaL) celebrated its centenary in 1994. The Journal operated regularly 1893-1914, 1925-1939, and from 1947 till today. Its problem solvers included Paul Erdős, Ferenc Mezei, furthermore George Polya, Gabriel Szegő, Laszlo Tisza and Laszlo Lovász, just to name a few. To have ones name on the list of the successful problem solvers has always been a source of pride for the school as well. The Journal is published monthly by the Eötvös Society in 8000 copies.
John von Neumann from Berlin wrote a letter to his professor Lipót Fejér in Budapest (1929) [Neumann Archive, OMIKK, Budapest]:
Dear highly honored Professor, I had the opportunity several times to speak to Leo Szilard about the student competitions of the Eötvös Mathematical and Physical Society, also about the fact that the winners of these competitions, so to say, overlap with the set of mathematicians and physicists who later became well-respected world-figures. Taking the general bad reputations of examinations world-wide into account it is to be considered as a great achievement if the selection works with a 50% probability of hitting the talent. Szilard is very interested in whether this procedure tan be applied in the German context and this has been the subject of much discussion between us. However, since we would like above all to learn what the reliable statistical details ere, we ere approaching you with the following request: We would like: 1. to have a list of names of the winners and runners-ups of the student competitions, 2. to see marked on the list those who were adopted on a scientific basis and those adopted for other work, 3. to know your opinion about the extent to which the prizewinners and the talented ere the same people and, for example, what proportion of the former would be worthy of financial support from the State in order to make their studies possible. Please forgive me for setting such a tiring tank but we would be very grateful to you for receiving of the information herein requested or, otherwise, an indication of how such information may be obtained.
Thanking you in advance, I remain your grateful pupil,
Neumann Jancsi
The Present: Student achievements
How well are our schools performing nowadays? Do they provide young with the skills and knowledge they will need to enter the labour market and to become lifelong learners who analyse, reason and communicate their ideas effectively? Parents, students, the general public and those responsible for running education systems all want to know: how well is the population being educated? The most common way of assessing educational outcomes at the student, institution and system levels is to measure the relative performance of students within each country. A school whose students perform well at examinations or gain admission the best universities is considered to have performed well [3].
Outcomes of the International Assessments in 1970, 1984 and 1994 of school children in science (age 14)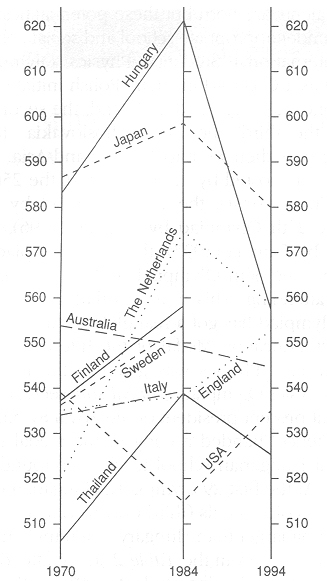
The most extended study has been performed by the International Association for the Evaluation of Educational Achievements (IEA). Several countries from Northern America, Europe, the Far East, and some countries from the Third World participated in these investigations in the past three decades, involving hundred thousands of students, selected carefully to represent the average performance of the countries in a statistically significant way. The test items show an Anglo-Saxon influence, they certainly differ from the style of the university entrance examinations practicized in the Continental Europe and the Orient [5].

Science is a rather compact and culture-independent body of knowledge. This is why educational experts consider the three IEA science studies to be the most informative assessment available till now for comparing educational performances in different countries. Students from twenty-odd countries have been tested from the age groups 10, 14, 18.
The comparison of the country scores in 1970 and 1984 and 1994 indicates, how reliable these rank orders are (Fig. 2). Experts devote highest attention to the scores of the age group 14, because they reflect the outcome of the primary school as well, and at this age in most countries practically the whole population goes to school. Hungary and Japan excel at the first and second assessments [6]. The Third International Mathematics and Science Study (IEA/TIMSS) was conducted during the school year 1994/95 by the IEA (Table 1).
The Future: Student competitions
The Hungarian Mathematical and Physical Society decided, that - to commemorate this period - launched yearly competitions to secondary school graduates. Later this has got the name Eötvös Competition. It was organized first in the fall of 1894, and it runs in every year (with the exception of a few war years). The problems given at this competitions are intended to assess the creativity (and not the memorized knowledge) of the students. The problems have to be solved in a closed room, supervised by impartial observes, within an afternoon. (Any book and tool can be used.) The respect of this competition is created - among others - by the fact that the 10 bests in mathematics and the 10 bests in physics have free admission to the university. (It has to be noted that students have been accepted at scientific, engineering and medical faculties only after passing very competitive entrance examinations. The Eötvös Competition is the favorite route for "wild" - a bit crazy - talents to university career. The professors immediately pay respect to an Eötvös medalist.)
This statistics of the first 29 olympiads indicates the total Number of participated students (N), the overall numbers of Gold (G), Silver (S), Bronze (B) medals and Honors (H) won by them, finally the Ratio (R) the successful students (having obtained medal or honor) compared to the participating students. Only "golden countries" having received gold medals are listed.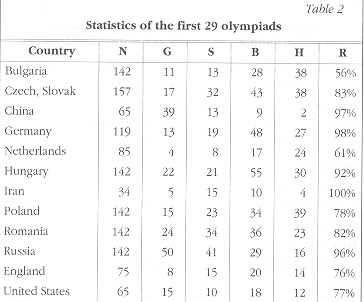
The source of the reputation of the Eötvös Competition is that its present winners find forerunners like Theodore von Kármán in mathematics (1897), Leo Szilard in physics (1916), Edward Teller in both, mathematics and physics (1925), as well as Lipót Fejér, Marcel Riesz, Gabriel Szegő, Laszlo Tisza, Ferenc Mezei, John C. Harsanyi, among earlier medalists. Theodore von Kármán and John G. Kemeny recommended such competitions for the U.S. In the 1950s George Polya (1887-1986) and Gabriel Szegő (1895-1986), professors at Stanford University, organized competitions in California according to the pattern of the Eötvös Competition. (Local physics competitions are organized in several districts of Hungary. Leo Szilard might be happy to know that there is a Szilard Competition for high school students in nuclear issues each year.)
The centenary of the Eötvös Competition was celebrated in 1994 in the presence of leading representatives of the International Union for Pure and Applied Physics (IUPAP), the International Group on Research in Physics Education (GIREP) and the European Physical Society (EPS). At this centenary celebration Kai-hua Zhao, vicepresident of the Chinese Physical Society, stressed that the Eötvös Competition might be considered as the forerunner of the International Physics Student Olympiad.
To compare the best talents in different countries the International Student Olympiads offer a chance. In every year, the five best students take part at the Olympiad, independently of the fact whether 1, 10, 100 or 1000 million people live in the country. These students - after having completed highschool studies - solve the same theoretical and experimental problems, given always by the host country of the Olympiad in the mother tongue of the students. Potential talents are born but these potentialities are realized only under appropriate school and social conditions.
The International Students' Physics Olympiad was conceived as a Czech-Hungarian-Polish initiative (1964). The first one was organized in Poland, the second one in Hungary, the third one in Czechoslovakia. It moved around Europe, then went to America and Asia. The 24th Olympiad was hosted by the U.S. (1993), the 25th Olympiad by China (1994), the 2óth Olympiad by Australia (1995), the 27th Olympiad by Norway (1996), the 28th Olympiad by Canada (1997), the 29th Olympiad by Iceland (1998), the 30th Olympiad by Italy (1999), with 60 countries attending. This indicates that the International Physics Olympiad has got a real global character. In 1991 the Physics Education Medal of the International Union for and Applied Physics was given to the International Students' Physics Olympiad. Jan Nilsson, secretary general of IUPAP, at present president of the Royal Swedish Academy of Science, handed a copy of the medal to Rudolf Kunfalvi, a Hungarian school teacher, co-founder of the Olympiad. At the first 29 olympiads, Hungarian teenagers collected 22 gold medals (third only to China and Russia, countries a bit larger than Hungary of ten million people).
As one can see from the Table 2, at the attended olympiad, 100% of the Iranian students, 98% of the German students, 97% of the Chinese students and 92% of the Hungarian students returned home with medal or honor. But not only Hungarian boys excel. Kate Varju turned out to be the best girl in the world at the 1991 physics olympiad.
The IEA study and the Olympiad complement each other. E.g. Japan scores well at IEA but does not participate at the Olympiad. Germany scores well at the Olympiad but it participated only at the first IEA science study where she performed well. One may hope that the view will become wider in the 2lst century, both at coming IEA studies and at the Olympiad. Hungary, this small and poor country perform well in most educational indicators, but she underpays her teachers, offers only a tight budget to the schools. Her economy is weak generally, carrying the burden of a high dept. Does this case disprove correlation between education and economy?
Physics education is so important that we must not hesitate to do much more for its improvement. Not only physics teachers but also the professor's (who educate them but who like to base their self-concept exclusively on their physics research and neglect the development of their own teaching) should keep in mind what L. Ledermann said [4]: "I relate the future of science education to the future of science."
References