Fizikai Szemle 2006/12. 393.o.
VOLT-E (VAN-E) FÁZISÁTMENET A BIG BANG
(LITTLE BANG) SORÁN?
Fodor Zoltán, Katz Sándor
ELTE TTK Elméleti Fizikai Tanszék
Általában nem vitatott nézet, hogy a legalapvetőbb fizikai
elmélet az elemi részek fizikája. A részecskefizikusok a
természet legkisebb építőköveit keresik, azok tulajdonságait
kívánják megérteni, és bíznak abban, hogy az ezekből
felépülő bonyolultabb rendszerek leírásához is el
lehet majd jutni. A megismerés során a kísérletek és az
elméleti vizsgálatok szoros kölcsönhatásban - és egymásrautaltságban
- haladnak. A kísérletek által felfedezett
részecskéket és kölcsönhatásokat az elméleti fizikusok
foglalják egységes képbe, a kikristályosodó alapvető
egyenleteket is ők oldják meg. A kísérletek alapja legtöbbször
részecskék ütköztetése részecskegyorsítóban.
Ilyenkor néhány nagyenergiás részecske vesz részt a
vizsgált folyamatban. Sokkal több nagyenergiás elemi
részecskével találkozhatunk például a korai Világegyetemben
(Big Bang, "Nagy Bumm", az angol nyelvtől elszakadva
"Ősrobbanás"), vagy az azt legközelebbről utánzó
földi kísérletekben a nehézionok ütközése során (Little
Bang, "Kis Bumm").
Igen fontos, alapvető kérdés, hogy volt-e, van-e - az
erős kölcsönhatás miatt fellépő - "fázisátmenet" a Big
Bang és a Little Bang során. Erre a kérdésre keresett és
talált egy nagy visszhangot keltett választ kutatócsoportunk
(Yasumichi Aoki, Endrődi Gergely, Fodor Zoltán,
Katz Sándor és Szabó Kálmán). Az eredmény a sokak
által a világ legrangosabb tudományos folyóiratának tartott
Nature -ben jelent meg ez év októberében, melyhez
ugyanazon folyóiratszámban a 2004. évi fizikai Nobel-díjas,
Frank Wilczek írt egy figyelemfelkeltő kísérőcikket.
Az erős kölcsönhatást mai tudásunk szerint leíró fizikai
elmélet a kvantum-színdinamika. A kvantum-színdinamikai
kölcsönhatás rendkívül erős. Egy "legyengített",
leárnyékolt fajtája felel a magerőkért, azok "hétköznapi"
megnyilvánulásaiért: az atombomba pusztító erejéért és a
Napban felszabaduló óriási energiáért.
Az elektromágneses kölcsönhatáshoz hasonlóan itt is
töltések játsszák a fő szerepet. Amíg azonban elektromos
töltés csak egyetlen fajta van (amely, persze, lehet pozitív
vagy negatív), a kvantum-színdinamikában többfajta töltés
is szerepel (ezek mindegyike is lehet pozitív vagy
negatív). Érdekes módon nemcsak az azonos fajtájú,
egyenlő mennyiségű pozitív és negatív töltések keveréke
eredményez semleges rendszert, hanem több, különböző
fajtájú töltés megfelelő arányú vegyítése is. Ez emlékeztet
a színek elméletére: a három alapszín keveréke fehér,
azaz "semleges" színt eredményez. Ezen analógia miatt
szokás az erős kölcsönhatás elméletét kvantum-színdinamikának
(kvantum-kromodinamikának) hívni. Az elektrodinamikai
töltést hordozó elektron kvantum-színdinamikai
analogonjainak - három van belőlük, kvarkoknak
hívjuk őket - három különböző töltését színtöltésnek,
sőt, gyakran piros, zöld és kék színtöltésnek nevezzük.
Természetesen a gondolatmeneteinkben említett színtöltéseknek
semmi közük sincs a valódi színekhez, az elnevezés
pusztán a mondott analógián alapul.
Az erős kölcsönhatás - ahogy már említettük - "rendkívül
erős". Álló töltéseinek szétválasztásakor, azaz két
kvark eltávolításakor, az elektromosságban szokásos 1 / r
típusú, a távolsággal csökkenő potenciál helyett egy minden
határon túl növő lineáris potenciál jelenik meg. Ez azt
is jelenti, hogy színtöltéseket közönséges körülmények
között nem lehet (makroszkopikus távolságra) széthúzni.
Egy ilyen szétválasztáshoz a potenciál legyőzésére, óriási
energiára volna szükség. Ezzel függ össze, hogy a természetben
csak zérus színtöltésű részecskéket detektálhatunk.
Ez megvalósulhat például úgy, hogy egy összetett
részecskében egy adott színtöltés pozitív és negatív járulékai
kioltják egymást. Az ilyen részecskéket legegyszerűbben
egy kvark (pozitív színtöltésű részecske) és egy antikvark
(negatív színtöltésű részecske) kötött állapotaként
értelmezzük, és mezonoknak hívjuk (például 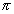 - vagy
K-mezonok). A másik lehetőség az, hogy a három színt
egyforma arányban keverjük. Az ilyen részecskéket három,
különböző színtöltésű kvark (vagy három antikvark)
kötött állapotaként értelmezzük, és barionoknak hívjuk
(ilyen például a proton vagy neutron). Összefoglalva azt
mondhatjuk, hogy az erős kölcsönhatás erőssége, a statikus
kvarkok között ható lineáris potenciál minden határon
túli növekedése felel azért, hogy a protonokban található
három kvark bezáródott. A szokásos anyag (protonok,
neutronok) az úgynevezett bezáró (angolul confined)
vagy más néven hadronikus fázisban található.
Ahogy láttuk, közönséges körülmények között nem
nyílik lehetőség szabad kvarkok észlelésére. A már említett
F. Wilczek, valamint D.J. Gross és H.D. Politzer azt
ismerték fel, hogy az energia növekedésével az erős kölcsönhatás
egyre "gyengül". Ezért a felismerésért kaptak
2004-ben Nobel-díjat. A lineárisan növekvő potenciál
statikus kvarkok esetén maradéktalanul érvényesülő bezáró
hatásával szemben az egyre magasabb hőmérsékleteken
fellépő egyre nagyobb energiák a kölcsönhatás
gyengüléséhez vezetnek, a színtöltések egyre jobban
eltávolodhatnak egymástól, mígnem ezt az eltávolodást
már nem is a visszahúzó potenciál, hanem a rendszerben
lévő többi részecske, az azokon való szóródás, az azokkal
történő ütközés korlátozza. Ilyen állapotban a színtöltött
részecskék lényegében már nem is érzik a bezárást.
Egy új fázis jelenik meg, melyet felszabadító (angolul
deconfined) fázisnak nevezünk.
A bezáró és a felszabadító fázisok között rendkívül
lényeges különbségek vannak. Alacsony hőmérsékleten
- a bezáró fázisban - csak semleges színtöltésű részecskéket
találunk, a kvarkok közötti potenciál minden határon
túl nő, és az ilyen állapotban (fázisban) levő kölcsönható
gáz mindössze néhány szabadsági fokkal rendelkezik.
Magas hőmérsékleten - a felszabadító fázisban - a
domináns részecskék színtöltöttek, a potenciál nem bezáró,
és az ilyen állapotban (fázisban) levő kölcsönható gáz
sok tucat szabadsági fokkal rendelkezik. Az állapot jellegét
meghatározó külső feltételek, például a hőmérséklet
változtatását kísérő - ennyire jelentősen eltérő állapotok
közötti - állapotváltozás során általában jellegzetes fázisátmenetet
szoktunk észlelni.
Közismert fázisátmenet például a víz és a gőz közötti
átmenet, melyet a hőmérséklet-nyomás, (T, p ), diagramon
az 1. ábra illusztrál. (Az ilyen típusú diagramokat
fázisdiagramnak szokás nevezni, mert egy anyag különböző
fázisait jelzi a külső paraméterek függvényében.)
Amint az ábra mutatja, alacsony hőmérsékleten a rendszer
a vízfázisban található. Viszonylag kis nyomáson, a
rendszert felmelegítve egy úgynevezett elsőrendű víz-
gőz fázisátmenetet észlelünk. Az elsőrendű fázisátmenetek
tipikusan nem folytonosak, nem analitikusak. A víz-
gőz fázisátmenet során a sűrűség nem folytonosan változik,
hanem ugrik (légköri nyomáson az 1 gramm/köbcentiméter
értékről egy nagyságrendekkel kisebb értékre),
illetve a fajhő végtelenné válik (a látens hőt közölni
kell a rendszerrel még mielőtt annak hőmérséklete akár a
legkisebb mértékben is változna). Ezt az elsőrendű fázisátmeneti
tartományt folytonos vonal mutatja. Érdemes
megjegyezni, hogy szennyezés mentes esetben és gyors
hőmérsékletváltozás mellett az elsőrendű fázisátmeneteket
túlhűlés vagy túlmelegedés jellemzi. Például a gőzfázis
a kritikus hőmérséklet alá hűl, majd rendkívül
gyorsan
vízcseppek jelennek meg. Ezen cseppek növekedése
viszi át a rendszert az egyik fázisból a másikba. (A fordított
irányú átmenet során lehetséges túlmelegedés jelensége,
ismert módon, felléphet víz mikrohullámú sütőben
történő melegítésekor.)
A fázisdiagram egyik legérdekesebb tulajdonsága a
kritikus "végpont" megjelenése. A víz 374 Celsius fokon
és 0,32 kg/l sűrűségen opálossá válik, makroszkopikus
méretű korrelációk alakulnak ki. Érdemes megjegyezni,
hogy ez az állapot akár egy gázláng segítségével is megvalósítható
(bár a fellépő nagy nyomás miatt meglehetősen
erős tartályra van szükség). Ebben a kritikus végpontban
másodrendű fázisátmenetet észlelünk. Itt a változások
folytonosak, de nem analitikusak. A rendszer
kritikus tulajdonságokat mutat, például a korrelációs
hossz végtelenné válik.
- vagy
K-mezonok). A másik lehetőség az, hogy a három színt
egyforma arányban keverjük. Az ilyen részecskéket három,
különböző színtöltésű kvark (vagy három antikvark)
kötött állapotaként értelmezzük, és barionoknak hívjuk
(ilyen például a proton vagy neutron). Összefoglalva azt
mondhatjuk, hogy az erős kölcsönhatás erőssége, a statikus
kvarkok között ható lineáris potenciál minden határon
túli növekedése felel azért, hogy a protonokban található
három kvark bezáródott. A szokásos anyag (protonok,
neutronok) az úgynevezett bezáró (angolul confined)
vagy más néven hadronikus fázisban található.
Ahogy láttuk, közönséges körülmények között nem
nyílik lehetőség szabad kvarkok észlelésére. A már említett
F. Wilczek, valamint D.J. Gross és H.D. Politzer azt
ismerték fel, hogy az energia növekedésével az erős kölcsönhatás
egyre "gyengül". Ezért a felismerésért kaptak
2004-ben Nobel-díjat. A lineárisan növekvő potenciál
statikus kvarkok esetén maradéktalanul érvényesülő bezáró
hatásával szemben az egyre magasabb hőmérsékleteken
fellépő egyre nagyobb energiák a kölcsönhatás
gyengüléséhez vezetnek, a színtöltések egyre jobban
eltávolodhatnak egymástól, mígnem ezt az eltávolodást
már nem is a visszahúzó potenciál, hanem a rendszerben
lévő többi részecske, az azokon való szóródás, az azokkal
történő ütközés korlátozza. Ilyen állapotban a színtöltött
részecskék lényegében már nem is érzik a bezárást.
Egy új fázis jelenik meg, melyet felszabadító (angolul
deconfined) fázisnak nevezünk.
A bezáró és a felszabadító fázisok között rendkívül
lényeges különbségek vannak. Alacsony hőmérsékleten
- a bezáró fázisban - csak semleges színtöltésű részecskéket
találunk, a kvarkok közötti potenciál minden határon
túl nő, és az ilyen állapotban (fázisban) levő kölcsönható
gáz mindössze néhány szabadsági fokkal rendelkezik.
Magas hőmérsékleten - a felszabadító fázisban - a
domináns részecskék színtöltöttek, a potenciál nem bezáró,
és az ilyen állapotban (fázisban) levő kölcsönható gáz
sok tucat szabadsági fokkal rendelkezik. Az állapot jellegét
meghatározó külső feltételek, például a hőmérséklet
változtatását kísérő - ennyire jelentősen eltérő állapotok
közötti - állapotváltozás során általában jellegzetes fázisátmenetet
szoktunk észlelni.
Közismert fázisátmenet például a víz és a gőz közötti
átmenet, melyet a hőmérséklet-nyomás, (T, p ), diagramon
az 1. ábra illusztrál. (Az ilyen típusú diagramokat
fázisdiagramnak szokás nevezni, mert egy anyag különböző
fázisait jelzi a külső paraméterek függvényében.)
Amint az ábra mutatja, alacsony hőmérsékleten a rendszer
a vízfázisban található. Viszonylag kis nyomáson, a
rendszert felmelegítve egy úgynevezett elsőrendű víz-
gőz fázisátmenetet észlelünk. Az elsőrendű fázisátmenetek
tipikusan nem folytonosak, nem analitikusak. A víz-
gőz fázisátmenet során a sűrűség nem folytonosan változik,
hanem ugrik (légköri nyomáson az 1 gramm/köbcentiméter
értékről egy nagyságrendekkel kisebb értékre),
illetve a fajhő végtelenné válik (a látens hőt közölni
kell a rendszerrel még mielőtt annak hőmérséklete akár a
legkisebb mértékben is változna). Ezt az elsőrendű fázisátmeneti
tartományt folytonos vonal mutatja. Érdemes
megjegyezni, hogy szennyezés mentes esetben és gyors
hőmérsékletváltozás mellett az elsőrendű fázisátmeneteket
túlhűlés vagy túlmelegedés jellemzi. Például a gőzfázis
a kritikus hőmérséklet alá hűl, majd rendkívül
gyorsan
vízcseppek jelennek meg. Ezen cseppek növekedése
viszi át a rendszert az egyik fázisból a másikba. (A fordított
irányú átmenet során lehetséges túlmelegedés jelensége,
ismert módon, felléphet víz mikrohullámú sütőben
történő melegítésekor.)
A fázisdiagram egyik legérdekesebb tulajdonsága a
kritikus "végpont" megjelenése. A víz 374 Celsius fokon
és 0,32 kg/l sűrűségen opálossá válik, makroszkopikus
méretű korrelációk alakulnak ki. Érdemes megjegyezni,
hogy ez az állapot akár egy gázláng segítségével is megvalósítható
(bár a fellépő nagy nyomás miatt meglehetősen
erős tartályra van szükség). Ebben a kritikus végpontban
másodrendű fázisátmenetet észlelünk. Itt a változások
folytonosak, de nem analitikusak. A rendszer
kritikus tulajdonságokat mutat, például a korrelációs
hossz végtelenné válik.
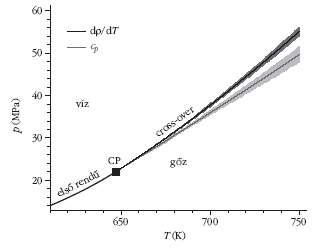
1. ábra. A víz sematikus fázisdiagramja hőmérséklet (T) nyomás (p)
síkon. A fázisvonal azon p-T értékeket jelöli, ahol a két fázis (víz és
gőz) tud együtt létezni. Közönséges légköri nyomáson (1 atm.) 100 Celsius
fokon, a légköri nyomás felénél 82 fokon. A víz és gőz közötti fázisvonal
végét egy kritikus pont jelöli. Ezen p-T értékpárnál a fázisátmenet
másodrendű. Ilyen T és p értékek esetén a víz opálossá válik, a
korrelációs hosszak végtelen nagyok lesznek. A jelenséget kritikus opaleszcenciának
hívjuk. Ezen kritikus ponthoz tartozó (T, p) értékeknél is
nagyobb hőmérsékleten és nyomáson már csak egy analitikus átmenetet
tapasztalunk, melynek átmeneti hőmérséklete a vizsgált mennyiségtől
függ. Más átmeneti hőmérsékletet ad a fajhő maximuma (alsó, világosabb
vonal és a bizonytalanságát jelző sáv), és megint mást a sűrűség
hőmérséklet szerinti deriváltjának maximuma (felső, sötétebb vonal és
a bizonytalanságát jelző sáv).
Ha a hőmérséklet-nyomás diagramon még ezeknél az
értékeknél is magasabb (T, p) értékeket vizsgálunk,
akkor egy analitikus átmenetet tapasztalunk (ezt szokás
crossover-átmenetnek is nevezni). A víz és a gőz közötti
tipikus különbségek részben megmaradnak, az átmenet
nem ugrásszerű, hanem folytonos és analitikus. A rendparaméternek
tekinthető sűrűség a crossoveren való áthaladáskor
is gyorsan változik, de a fázisátmenetekre
jellemző szingularitás nem jelenik meg. A sűrűség nem
ugrásszerűen, hanem folytonosan változik, de a változásban
van egy meredek szakasz, melynek legmeredekebb
pontját a víz forráspontjának tekinthetjük. A fajhőnek is
van egy maximuma (amely az elsőrendű fázisátmeneti
tartománnyal ellentétben már nem végtelen). Az átmeneti
hőmérsékletet, a víz forráspontját ezzel a maximummal is
definiálhatjuk. Ahogy az 1. ábra mutatja, a két definíció
megegyezik az első és másodrendű fázisátmenetek esetén.
Az analitikus átmenet (crossover) viszont más forráspontot,
átmeneti hőmérsékletet eredményez attól függően,
hogy melyik definíciót használjuk.
A víz fázisdiagramja arra a kérdésre mutatja a választ,
hogy mi történik a vízzel, ha egyre jobban melegítjük,
vagy egyre jobban összenyomjuk. A kérdést a részecskefizikában
sokkal általánosabban is feltehetjük. Mi történik a
"semmivel", a vákuummal, ha egyre jobban "melegítjük"?
A vákuum melegítése (energia bepumpálása) azzal jár,
hogy tömeggel rendelkező részecskék jelennek meg. Ez
az E = m c2 képlet szerinti energia-tömeg ekvivalencia
következménye. Természetesen óriási hőmérsékletekre
van szükség, hogy az erős kölcsönhatásban részt vevő
részecskék a melegítés hatására megjelenjenek a vákuumban.
Tipikusan 1012 Celsius fok körüli értékre kell
gondolnunk. Ha a hőmérsékletet tovább növeljük, akkor
egy fázisátmenetet tapasztalunk: a bezárt kvarkok a már
leírt módon kiszabadulnak.
Ilyen magas hőmérsékletek uralkodhattak a korai Világegyetemben
(Big Bang), annak körülbelül 10 mikroszekundumos
korában. Nehézionok ütköztetése révén
sikerült ilyen magas hőmérsékleteket földi körülmények
között is előállítani. Jelenleg az Egyesült Államok Brookhaven
National Laboratory-jának (BNL) Relativisztikus
Nehézion Ütköztetője (Relativistic Heavy Ion Collider,
RHIC) szolgáltatja a legmagasabb hőmérsékleteket. Igaz,
ez a magas hőmérséklet csak a másodperc töredékéig áll
fenn, a rendszer igen nagy sebességgel kitágul és lehűl
(Little Bang).
Mit tudunk mondani az erős kölcsönhatás miatt megvalósuló
átmenetről? A bezáró és a felszabadító fázis közötti
különbség olyan jelentős, hogy évtizedekig meg volt
győződve a tudományos közvélemény arról, hogy közöttük
egy elsőrendű fázisátmenetnek kell történnie. Egy
ilyen, a korai Világegyetemben végbement elsőrendű fázisátmenetet
az Univerzum gyors tágulása miatt a már
említett túlhűlés jellemez. A hadronikus, bezáró fázis
cseppecskéi robbanásszerűen jelennek meg a felszabadító
fázisban. Ez máig ható következményekkel járt volna.
Nézzünk néhányat az ilyen jellegű fázisátmenet következményei
közül. A cseppecskék vonzó tömegcentrumokat
képeznek, a Világegyetem tömegeloszlása ennek következtében
megváltozik. Az atommagok képződése is
inhomogén módon zajlik le. Egzotikus ritka kvarkokat
tartalmazó csomagocskák keletkeznek. Az egymásnak ütköző
cseppecskék gravitációs hullámokat keltenek. Kísérleti
fizikusok egész generációja kereste ezen jelenségek
mai megnyilvánulásait. Sajnos, a kísérletek nem voltak
elég érzékenyek, legalábbis néhányan így értékelték
azt a tényt, hogy a keresés ezidáig sikertelen maradt. Sokan
mások viszont már kezdték feladni az elsőrendű fázisátmenetre
vonatkozó képet. Voltak jelek, melyek arra
utaltak, hogy talán egy analitikus átmenettel állunk szemben.
Egyre többen vallották ezt a nézetet, noha egyértelmű
bizonyíték sem ezt, sem az elsőrendű fázisátmenetre
vonatkozó elképzelést nem igazolta. A helyzet elméleti
bizonyítás szempontjából mindig is nyitott volt, és kísérleti
evidencia sem volt, mely az egyik vagy a másik forgatókönyvet
támogatta, vagy éppen kizárta volna.
Kutatócsoportunk elméleti számítások alapján megmutatta,
hogy az átmenet a nagy nyomású víz átmenetéhez
hasonlít, azaz analitikus átmenet, az elsőrendű átmenetekre
vonatkozó elképzeléseket el kell vetni. Az Univerzum
fejlődését egy folytonos átmenet segítségével kell
megértenünk. A víz forrását nap mint nap látjuk, és egy
egyszerű hőmérővel ellenőrizhetjük, hogy légköri nyomáson
valóban 100 Celsius fokon történik. A víz kritikus
pontjának helyét is a kísérletek adták meg, és a kísérletek
mondják meg azt is, hogy mely hőmérséklet-nyomás
értékek felett kapunk analitikus átmenetet. Elméletileg
ezek meghatározása rendkívül nehéz, alapelvekből ezidáig
nem is sikerült.
Hogyan lehetséges, hogy a víznél szemmel láthatólag
lényegesen egzotikusabb, bonyolultabbnak tűnő kvantum-
színdinamikai átmenetet sikerült mégis elméletileg
megérteni?
A részecskefizika kölcsönhatásait (a már említett erős
kölcsönhatás mellett ilyen a radioaktív béta-bomlásért
felelős gyenge kölcsönhatás és az elektronok és fotonok
kölcsönhatását leíró kvantum-elektrodinamika) a kvantumtérelméletek
írják le. Ezek egyrészt térelméletek, azaz
a dinamikai változókat, tereket, a geometriai tér pontjaihoz
rendeljük. (Analógiát keresve szemléletes példa lehet
a meteorológia. A hőmérséklet, nyomás, szélsebesség a
tér különböző pontjaiban más és más, és időben fejlődik.)
A kvantumtérelméletek másik jellemzője, hogy
kvantumelméletek. A legismertebb kvantumelmélet a
kvantummechanika, amelyben a dinamikai változókat, az
impulzust és a helyet nem számokkal, hanem egymással
fel nem cserélhető operátorokkal jellemezzük. Ennek
egyik jól ismert következménye a Heisenberg-féle határozatlansági
reláció, valamint az is, hogy, ha a leírt objektum
kötött állapot, annak energiája csak egymástól diszkréten
különböző értékeket vehet fel. A kvantumtérelméletek
ezen két leírási mód ötvözéséből születtek. A dinamikai
változók a terek, melyeket, a meteorológiával ellentétben,
már nem számokkal, hanem egymással fel
nem cserélhető operátorokkal írunk le. Ez az elmélet is
meghatározott, kvantált energiaszintekkel rendelkezik.
Az általa leírt objektumokhoz azonban már nemcsak
meghatározott energiát rendelhetünk, hanem a térbeli és
időbeli változások összekapcsoltsága miatt jól meghatározott
(kvantált) impulzust, impulzusmomentumot és
részecskeszámot is.
Felmerülhet a gondolat, hogy az elemi részecskéket
kvantumtérelméleti objektumokként, mint térkvantumokat
írjuk le. Rendkívül meglepő, hogy ezt az elképzelést két -
legalábbis távolról nézve - egyszerű feltétellel kiegészítve
az elemi részek világának szinte minden jelensége nagy
pontossággal leírható. Az egyik feltétel az önellentmondásmentesség
(ezt minden végső elmélettől természetesen
elvárjuk). A másik feltétel, hogy az elmélet alapegyenleteit
bizonyos transzformációknak változatlanul kell hagyniuk
(szimmetriatranszformációk). A kvantum-elektrodinamikában
ez a transzformáció az anyagtereknek egységnyi abszolút
értékű komplex számmal való megszorzása. A gyenge
kölcsönhatás esetében a szorzás 2 x 2-es (speciális unitér)
mátrixokkal, az erős kölcsönhatás kvantum-színdinamikai
elmélete esetében pedig 3 x 3-as (ugyancsak speciális
unitér) mátrixokkal történik. Ezeknek az egyszerű transzformációknak,
ha szimmetriatranszformációk, jól meghatározott
alakban leírható kölcsönhatások, dinamikai egyenletek
felelnek meg. Ezek birtokában, az egyenletek megoldásával,
elvileg lehetőség nyílik a megfelelő fizikai rendszer
történéseinek leírására, így a kvantum-színdinamikai
fázisátmenet közelítésektől mentes leírására is. A gyakorlatban
egzakt megoldásokat csak kivételes esetekben sikerül
találni, úgyhogy a feladatot még az egyenletekben rejlő
információ kikutatására alkalmas közelítő módszer megtalálása,
kidolgozása is nehezíti.
A részecskefizikai folyamatok közelítő leírásának egyik
legfontosabb módszere a perturbációszámítás, a fokozatos
közelítések módszere. Ezen módszer alkalmazásának első
lépése az, hogy valamely fizikai mennyiséget közelítőleg
kiszámítunk, majd ezt az eredményt a számítás további
lépéseiben újra meg újra korrigáljuk. Amennyiben a korrekciók
kicsik, és a közelítés során ráadásul még egyre
kisebbekké is válnak, a módszer fokozatosan közelíti a
végeredményt. A módszer alkalmazhatóságának feltétele
- a fizikai probléma terminológiájával élve -, hogy a kölcsönhatás
gyenge legyen. Sajnos, az erős kölcsönhatás -
"erős", a fokozatos közelítések módszere, néhány kivételes
esettől eltekintve, nem alkalmazható.
Alternatívát a rácstérelmélet kínál. Az alapvető rácstérelméleti
közelítés abban áll, hogy a teret és időt nem
folytonos változókként kezeli, hanem egy ráccsal helyettesíti.
(Hasonló rácsot használnak az időjárás-előrejelzés
készítése során. Meghatározott földrajzi helyeken és magasságokban
mérik a hőmérsékletet, szélirányt, légnyomást,
majd az adatok összesítése és persze jelentős számolások
után készül el az előrejelzés.) A részecskefizikában
az elmélet térerősségeit írjuk a rácspontokba. Láttuk,
hogy kvantumelméleteket egymással fel nem cserélhető
operátorok segítségével fogalmazhatjuk meg. Létezik
azonban egy másik (R. Feynman Nobel-díjas amerikai
fizikus nevéhez fűződő), pályaintegrálos megfogalmazás,
amely jobban illeszkedik a rácsformalizmushoz. A kvantummechanikai
átmeneti valószínűséget úgy határozzuk
meg, hogy minden létező klasszikus pályára összeadjuk
az exp(iS ) fázisfaktorokat (i a képzetes egységgyök, S az
adott klasszikus pályához tartozó hatás). A klasszikus fizikában
egyetlen pálya valósul meg, és ezt a hatás minimális
értéke választja ki. A módszer térelméleti általánosítása
abban áll, hogy az exp(iS ) fázisfaktorokat minden létező
térkonfigurációra összegezzük. Mivel az exp(iS ) fázisfaktorok
erősen oszcillálnak, összegzésük numerikus módszerekkel
nehéz. Ezért a jelenségeket általában imaginárius
idő függvényeként vizsgáljuk, mely ekvivalens az
exp(-S ) Boltzmann-faktorok összegzésével. Ezen összeg
tagjai már nem oszcillálnak, a számítás elvégezhető.
Meteorológiában a jóslatok annál jobbak, minél finomabbak
a számításhoz használt rácsok. Ez azt jelenti,
hogy minél több pontban kell megmérnünk a hőmérsékletet,
nyomást, szélsebességet, és ezeket a finom rácson
elvégzett méréseket használjuk a számítások során. A
kvantumtérelméleti számítások nagyon hasonlóak. Minél
finomabb a rács, annál pontosabb az eredmény. Numerikus
számolások esetén a végtelen finomságú rácsot extrapolációval
szoktuk elérni. Egyre finomabb és finomabb
rácsokat használunk, majd az eredményeket, a rácsállandótól
való függésük aszimptotikus alakjának ismeretében,
a végtelen finom, azaz nulla rácsállandóhoz extrapoláljuk
(kontinuum határeset).
Az egyes jelenségeket az állapotösszeg numerikus
meghatározásának a révén, nagy számítógépekkel számítjuk
ki. Manapság 10 milliárd dimenziós integrálokat
számolunk. Másodperceként ezer milliárd műveletre van
szükség, amely szuperszámítógépeknek való feladat.
A 21. század elejének emblematikus szuperszámítógépe
volt például a japán Earth Simulator, Föld-számoló.
Másodpercenként sok ezer milliárd műveletet végez, de,
sajnos, az ára is a milliárd dollár nagyságrendjébe esik.
Számunkra ez az irány nem volt járható. Ezért az ELTE-n
kifejlesztettünk egy szuperszámítógépet, mely a részecskefizikai
felhasználásokban versenyképes a japán géppel,
de annak töredékébe kerül. Ez amiatt van, hogy mi személyi
számítógépekből építkezünk, és nem készen vesszük
a szuperszámítógépet. A személyi számítógépek a
számítási képességeikhez képest - óriási piacuk miatt -
nagyon olcsók. A hétköznapi életben a számítógépipar
egyik húzóereje a számítógépes játékok iránti igény. E
játékok megvalósítása során a háttérben olyan műveleti
struktúrát használnak fel, amely matematikai értelemben
nagyon hasonló (szakkifejezéssel: azzal lokálisan izomorf)
a standard részecskefizikai elmélet egyik szimmetriatranszformációjához.
Ameddig a személyi számítógépek
gyártói arra törekednek, hogy a játékprogramok minél
gyorsabban fussanak, és ennek megfelelően huzalozzák
be a processzorokat, addig az ezeket felhasználó részecskefizikai
számítások is egyre gyorsabbak lesznek. Persze,
a programozás terén el kell menni a megfelelő szintig.
Miután az erős kölcsönhatás elméleti hátterét megértettük,
és rendelkezünk a megfelelő számítógépes kapacitással,
hozzákezdhetünk az eredeti kérdésünk megválaszolásához,
nevezetesen, el kell döntenünk, hogy az erős
kölcsönhatás magas hőmérsékletű átmenete elsőrendű
fázisátmenet volt vagy egy analitikus crossover. A fázisátmenetekkel
kapcsolatos kérdések vizsgálatához az úgynevezett
véges méret skálázást szokás használni. A fázisátmenetekre
jellemző szinguláris viselkedés csak végtelen
térfogatú rendszerekben jelentkezik. Véges térfogaton
semmilyen szingularitást nem látunk. A fajhő nem
válik végtelenné (bár értéke elég nagy lesz), a víz sűrűsége
nem ugrik (bár igen gyorsan változik). Az analitikus,
crossover típusú átmenetekre viszont eredendően az
ilyen gyors, de szingularitástól mentes változás jellemző
mind véges, mind végtelen térfogaton. Hogyan tudunk
akkor különbséget tenni véges térfogaton vagy térfogatokon
egy valódi fázisátmenet és egy analitikus, crossover
típusú átmenet között? Erre a célra dolgozták ki a végesméret-
skálázás elméletét.
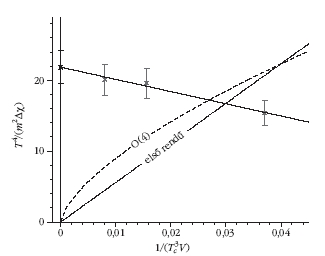
2. ábra. Az erős kölcsönhatás egyik (a víz fajhőjéhez hasonló)fizikai
mennyiségének vizsgálata. A hőmérséklet függvényében a maximumot
kerestük. A három pont a három különbözo térfogaton kapott eredményt,
illetve azok hibáját mutatja. A folytonos vonal jelzi a végtelen térfogati
extrapolációt. A pontozott, illetve szaggatott vonal jelzi a várt viselkedést
elsőrendű és másodrendű fázisátmenet esetén. A számítások teljesen
más, analitikus átmenetre jellemző térfogatfüggést mutatnak.
Egy valódi elsőrendű fázisátmenet esetén a fajhő (az
átmeneti hőmérsékleten) a térfogat növelésekor a térfogattal
arányosan, minden határon túl nő. A víz példájánál
maradva: a sűrűség hőmérséklet szerinti deriváltja, bár
nem végtelen (a sűrűség nem ugrik), de a rendszer méretének
növelésével, ugyancsak a térfogattal arányosan divergál.
A másodrendű fázisátmenetek hasonlóan viselkednek.
Az említett fizikai mennyiségek a térfogat növelésével
a másodrendű fázisátmenet esetében is divergálnak. A
legfontosabb különbség az, hogy ez a minden határon túl
történő növekedés nem a térfogattal, hanem annak valamilyen,
általában egynél kisebb, hatványával történik. A
divergencia megjelenik, de enyhébb formában. Analitikus,
crossover típusú átmenet esetén a kép teljesen más. A
megfelelő fizikai mennyiségek nem nőnek a térfogat növelése
során. Enyhe térfogatfüggést kell tapasztalnunk,
mely nagy térfogatokra fokozatosan eltűnik.
Számításaink során egy, a sűrűség deriváltjához hasonló
mennyiség hőmérsékletfüggését határoztuk meg
három különböző térfogaton és négy különböző térbeli
felbontás, rácsállandó mellett. (A konkrét mennyiség,
amelyet vizsgáltunk, a kvarkterek kondenzátuma, mely a
sűrűséggel analóg, illetve ezen kondenzátum hőmérséklet
szerinti deriváltja volt. Elsőrendű fázisátmenet esetén
a kondenzátum értéke ugrana, a kondenzátum hőmérséklet
szerinti deriváltja pedig végtelenné válna.)A tipikus
térbeli felbontás a meteorológiai felbontásokhoz képes
meglehetősen kicsiny 0,000 000 000 00001 cm. A négy
különböző felbontást használva mindhárom térfogaton
meghatároztuk a fenti fizikai mennyiség hőmérsékletfüggéséhez
tartozó maximumot. Ez a három különböző térfogaton
három különböző eredmény. A kérdés, hogy ez
a három eredmény a fázisátmenetekre jellemző térfogatfüggést
mutatja-e vagy sem. A 2. ábra illusztrálja a végeredményt.
A sűrűség hőmérséklet szerinti deriváltjához
hasonló mennyiség inverzét ábrázoljuk a térfogat inverzének
a függvényében. (Az egyszerűbb ábrázolás kedvéért
mindkét mennyiséget dimenziótlanítottuk a hőmérséklet
és a kvarktömeg segítségével.)A három térfogathoz
tartozó eredményt, valamint azok hibáját az ábra
pontjai mutatják. A végtelen térfogati határesetet a függőleges
tengely közvetlen környezete jelzi (hiszen a térfogat
inverzének függvényében ábrázoltuk az eredményt).
Valódi fázisátmenet esetén a vizsgált mennyiség a térfogat
növelésekor minden határon túl nőne, azaz az inverze
nullához tartana. Ez azt jelenti, hogy a három pontnak
az origóhoz kellene tartania. A két vonal jelzi, hogy ez
hogyan valósulna meg első-, illetve másodrendű fázisátmenet
esetén. Ahogy látható, az eredmények egyáltalán
nem ezt a fajta viselkedést mutatják. A térfogat növelésekor
a vizsgált mennyiség konstans értékhez tart. Az erős
kölcsönhatás átmenetéről így beláttuk, hogy az nem egy
valódi szingularitással jellemezhető fázisátmenet, hanem
egy analitikus, crossover típusú átmenet.
Összegzésképen a következőket mondhatjuk. Az
erős kölcsönhatás alacsony és magas hőmérsékleti viselkedése
jelentősen eltér. A két tartomány közötti átmenetet
alapelvek segítségével vizsgálhatjuk. A számítások
elvégzéséhez a saját fejlesztésű szuperszámítógépek
költségkímélő megoldást jelentettek. Az átmenetről
sikerült megmutatni, hogy az nem a víz forrásához hasonló
fázisátmenet, hanem egy analitikus, úgynevezett
crossover. Az átmenet típusának meghatározása a korai
Univerzum (Big Bang) és a jelenleg is folyó nehézionkísérletek
(Little Bang) folyamatainak megértése szempontjából
volt fontos.

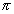 - vagy
K-mezonok). A másik lehetőség az, hogy a három színt
egyforma arányban keverjük. Az ilyen részecskéket három,
különböző színtöltésű kvark (vagy három antikvark)
kötött állapotaként értelmezzük, és barionoknak hívjuk
(ilyen például a proton vagy neutron). Összefoglalva azt
mondhatjuk, hogy az erős kölcsönhatás erőssége, a statikus
kvarkok között ható lineáris potenciál minden határon
túli növekedése felel azért, hogy a protonokban található
három kvark bezáródott. A szokásos anyag (protonok,
neutronok) az úgynevezett bezáró (angolul confined)
vagy más néven hadronikus fázisban található.
Ahogy láttuk, közönséges körülmények között nem
nyílik lehetőség szabad kvarkok észlelésére. A már említett
F. Wilczek, valamint D.J. Gross és H.D. Politzer azt
ismerték fel, hogy az energia növekedésével az erős kölcsönhatás
egyre "gyengül". Ezért a felismerésért kaptak
2004-ben Nobel-díjat. A lineárisan növekvő potenciál
statikus kvarkok esetén maradéktalanul érvényesülő bezáró
hatásával szemben az egyre magasabb hőmérsékleteken
fellépő egyre nagyobb energiák a kölcsönhatás
gyengüléséhez vezetnek, a színtöltések egyre jobban
eltávolodhatnak egymástól, mígnem ezt az eltávolodást
már nem is a visszahúzó potenciál, hanem a rendszerben
lévő többi részecske, az azokon való szóródás, az azokkal
történő ütközés korlátozza. Ilyen állapotban a színtöltött
részecskék lényegében már nem is érzik a bezárást.
Egy új fázis jelenik meg, melyet felszabadító (angolul
deconfined) fázisnak nevezünk.
A bezáró és a felszabadító fázisok között rendkívül
lényeges különbségek vannak. Alacsony hőmérsékleten
- a bezáró fázisban - csak semleges színtöltésű részecskéket
találunk, a kvarkok közötti potenciál minden határon
túl nő, és az ilyen állapotban (fázisban) levő kölcsönható
gáz mindössze néhány szabadsági fokkal rendelkezik.
Magas hőmérsékleten - a felszabadító fázisban - a
domináns részecskék színtöltöttek, a potenciál nem bezáró,
és az ilyen állapotban (fázisban) levő kölcsönható gáz
sok tucat szabadsági fokkal rendelkezik. Az állapot jellegét
meghatározó külső feltételek, például a hőmérséklet
változtatását kísérő - ennyire jelentősen eltérő állapotok
közötti - állapotváltozás során általában jellegzetes fázisátmenetet
szoktunk észlelni.
Közismert fázisátmenet például a víz és a gőz közötti
átmenet, melyet a hőmérséklet-nyomás, (T, p ), diagramon
az 1. ábra illusztrál. (Az ilyen típusú diagramokat
fázisdiagramnak szokás nevezni, mert egy anyag különböző
fázisait jelzi a külső paraméterek függvényében.)
Amint az ábra mutatja, alacsony hőmérsékleten a rendszer
a vízfázisban található. Viszonylag kis nyomáson, a
rendszert felmelegítve egy úgynevezett elsőrendű víz-
gőz fázisátmenetet észlelünk. Az elsőrendű fázisátmenetek
tipikusan nem folytonosak, nem analitikusak. A víz-
gőz fázisátmenet során a sűrűség nem folytonosan változik,
hanem ugrik (légköri nyomáson az 1 gramm/köbcentiméter
értékről egy nagyságrendekkel kisebb értékre),
illetve a fajhő végtelenné válik (a látens hőt közölni
kell a rendszerrel még mielőtt annak hőmérséklete akár a
legkisebb mértékben is változna). Ezt az elsőrendű fázisátmeneti
tartományt folytonos vonal mutatja. Érdemes
megjegyezni, hogy szennyezés mentes esetben és gyors
hőmérsékletváltozás mellett az elsőrendű fázisátmeneteket
túlhűlés vagy túlmelegedés jellemzi. Például a gőzfázis
a kritikus hőmérséklet alá hűl, majd rendkívül
gyorsan
vízcseppek jelennek meg. Ezen cseppek növekedése
viszi át a rendszert az egyik fázisból a másikba. (A fordított
irányú átmenet során lehetséges túlmelegedés jelensége,
ismert módon, felléphet víz mikrohullámú sütőben
történő melegítésekor.)
A fázisdiagram egyik legérdekesebb tulajdonsága a
kritikus "végpont" megjelenése. A víz 374 Celsius fokon
és 0,32 kg/l sűrűségen opálossá válik, makroszkopikus
méretű korrelációk alakulnak ki. Érdemes megjegyezni,
hogy ez az állapot akár egy gázláng segítségével is megvalósítható
(bár a fellépő nagy nyomás miatt meglehetősen
erős tartályra van szükség). Ebben a kritikus végpontban
másodrendű fázisátmenetet észlelünk. Itt a változások
folytonosak, de nem analitikusak. A rendszer
kritikus tulajdonságokat mutat, például a korrelációs
hossz végtelenné válik.
- vagy
K-mezonok). A másik lehetőség az, hogy a három színt
egyforma arányban keverjük. Az ilyen részecskéket három,
különböző színtöltésű kvark (vagy három antikvark)
kötött állapotaként értelmezzük, és barionoknak hívjuk
(ilyen például a proton vagy neutron). Összefoglalva azt
mondhatjuk, hogy az erős kölcsönhatás erőssége, a statikus
kvarkok között ható lineáris potenciál minden határon
túli növekedése felel azért, hogy a protonokban található
három kvark bezáródott. A szokásos anyag (protonok,
neutronok) az úgynevezett bezáró (angolul confined)
vagy más néven hadronikus fázisban található.
Ahogy láttuk, közönséges körülmények között nem
nyílik lehetőség szabad kvarkok észlelésére. A már említett
F. Wilczek, valamint D.J. Gross és H.D. Politzer azt
ismerték fel, hogy az energia növekedésével az erős kölcsönhatás
egyre "gyengül". Ezért a felismerésért kaptak
2004-ben Nobel-díjat. A lineárisan növekvő potenciál
statikus kvarkok esetén maradéktalanul érvényesülő bezáró
hatásával szemben az egyre magasabb hőmérsékleteken
fellépő egyre nagyobb energiák a kölcsönhatás
gyengüléséhez vezetnek, a színtöltések egyre jobban
eltávolodhatnak egymástól, mígnem ezt az eltávolodást
már nem is a visszahúzó potenciál, hanem a rendszerben
lévő többi részecske, az azokon való szóródás, az azokkal
történő ütközés korlátozza. Ilyen állapotban a színtöltött
részecskék lényegében már nem is érzik a bezárást.
Egy új fázis jelenik meg, melyet felszabadító (angolul
deconfined) fázisnak nevezünk.
A bezáró és a felszabadító fázisok között rendkívül
lényeges különbségek vannak. Alacsony hőmérsékleten
- a bezáró fázisban - csak semleges színtöltésű részecskéket
találunk, a kvarkok közötti potenciál minden határon
túl nő, és az ilyen állapotban (fázisban) levő kölcsönható
gáz mindössze néhány szabadsági fokkal rendelkezik.
Magas hőmérsékleten - a felszabadító fázisban - a
domináns részecskék színtöltöttek, a potenciál nem bezáró,
és az ilyen állapotban (fázisban) levő kölcsönható gáz
sok tucat szabadsági fokkal rendelkezik. Az állapot jellegét
meghatározó külső feltételek, például a hőmérséklet
változtatását kísérő - ennyire jelentősen eltérő állapotok
közötti - állapotváltozás során általában jellegzetes fázisátmenetet
szoktunk észlelni.
Közismert fázisátmenet például a víz és a gőz közötti
átmenet, melyet a hőmérséklet-nyomás, (T, p ), diagramon
az 1. ábra illusztrál. (Az ilyen típusú diagramokat
fázisdiagramnak szokás nevezni, mert egy anyag különböző
fázisait jelzi a külső paraméterek függvényében.)
Amint az ábra mutatja, alacsony hőmérsékleten a rendszer
a vízfázisban található. Viszonylag kis nyomáson, a
rendszert felmelegítve egy úgynevezett elsőrendű víz-
gőz fázisátmenetet észlelünk. Az elsőrendű fázisátmenetek
tipikusan nem folytonosak, nem analitikusak. A víz-
gőz fázisátmenet során a sűrűség nem folytonosan változik,
hanem ugrik (légköri nyomáson az 1 gramm/köbcentiméter
értékről egy nagyságrendekkel kisebb értékre),
illetve a fajhő végtelenné válik (a látens hőt közölni
kell a rendszerrel még mielőtt annak hőmérséklete akár a
legkisebb mértékben is változna). Ezt az elsőrendű fázisátmeneti
tartományt folytonos vonal mutatja. Érdemes
megjegyezni, hogy szennyezés mentes esetben és gyors
hőmérsékletváltozás mellett az elsőrendű fázisátmeneteket
túlhűlés vagy túlmelegedés jellemzi. Például a gőzfázis
a kritikus hőmérséklet alá hűl, majd rendkívül
gyorsan
vízcseppek jelennek meg. Ezen cseppek növekedése
viszi át a rendszert az egyik fázisból a másikba. (A fordított
irányú átmenet során lehetséges túlmelegedés jelensége,
ismert módon, felléphet víz mikrohullámú sütőben
történő melegítésekor.)
A fázisdiagram egyik legérdekesebb tulajdonsága a
kritikus "végpont" megjelenése. A víz 374 Celsius fokon
és 0,32 kg/l sűrűségen opálossá válik, makroszkopikus
méretű korrelációk alakulnak ki. Érdemes megjegyezni,
hogy ez az állapot akár egy gázláng segítségével is megvalósítható
(bár a fellépő nagy nyomás miatt meglehetősen
erős tartályra van szükség). Ebben a kritikus végpontban
másodrendű fázisátmenetet észlelünk. Itt a változások
folytonosak, de nem analitikusak. A rendszer
kritikus tulajdonságokat mutat, például a korrelációs
hossz végtelenné válik.
